點擊機械波的多解問題
林 瀚
(廣東省汕頭市金山中學)
多解問題是機械波中的重點和難點,其產生的根本原因是機械波傳播方向不確定、傳播距離和波長關系不確定、振動時間和振動周期不確定等因素,以下結合例題作一探討!
1 傳播方向不確定導致多解
波源起振后產生的波可以在介質中向四周傳播.有些試題并未明確波的傳播方向,此時,要分類討論波的傳播方向,進而出現多解.
例1一列簡諧橫波在介質中傳播,在其傳播方向上存在兩個質點A和B,相距1.2m.假設在某一時刻,A質點正好由平衡位置向上運動,而B質點在波谷處.已知該波傳播的速度是48 m·s-1,兩質點的距離在2個波長和6個波長之間.求該波頻率的最大值.
解析
若波由A向B傳播,最短波長應滿足

又因為v=fλ,可得最大頻率f=210 Hz;若波由B向A傳播,最短波長應滿足
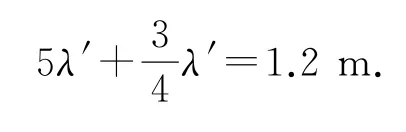
又因為v=f′λ′,可得最大頻率f′=230 Hz,通過比較可知,該簡諧橫波的最大頻率為230Hz.
點評
兩個方向傳播,導致兩個方向的多解,由于有約束條件,即要求波速最大,波長最短,因此波長不存在多解.
2 傳播距離與波長關系不確定導致多解
在波的傳播方向上,相隔一個波長的質點振動步調是完全相同的,假設題目中沒有具體規定波的傳播距離和波長的關系,就會存在多解.
例2一列機械橫波在均勻介質中沿著x軸傳播,此時的波形圖如圖1所示.在x軸上存在著質點P和質點Q,它們的平衡位置坐標分別為0.4 m和0.7m.從該時刻開始計時:
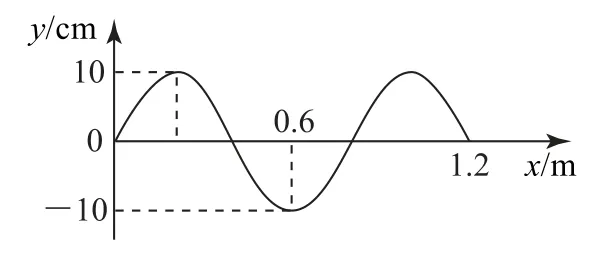
圖1
(1)如果P質點連續兩次經過x軸的時間差為Δt=0.4s,那么波的傳播速度為多大?
(2)如果在0.1s時Q質點運動到波谷處,那么波的周期是多少?
解析
(1)由題意可知,波的周期
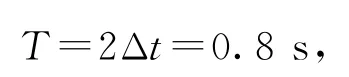
波長λ=0.8m,根據可得
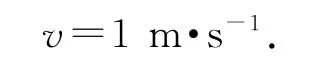
(2)若波沿x軸正方向傳播,則在t時間內,波的傳播距離為
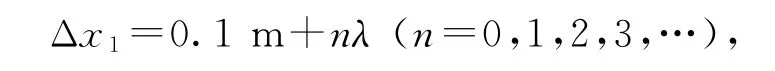
波的傳播速度為
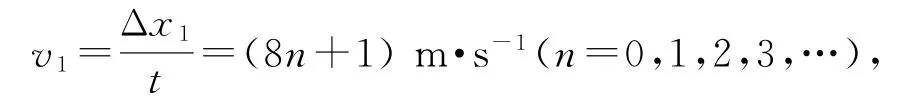
周期為
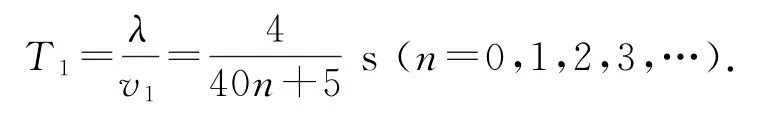
若波沿x軸負方向傳播,則在t時間內,波的傳播距離為
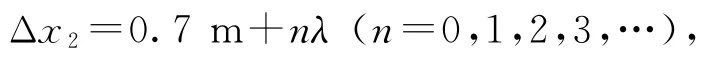
波的傳播速度為
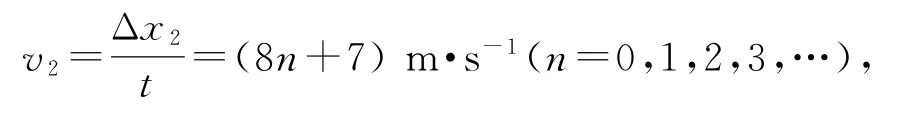
周期為
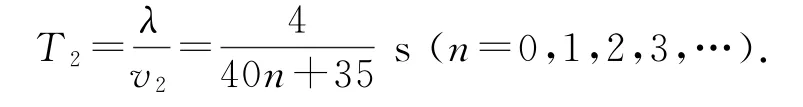
點評
解題時一般采用從特殊到一般的思維方法,即找出一個周期內滿足條件的關系Δt或Δx,若此關系為時間,則t=nT+Δt(n=0,1,2,…);若此關系為距離,則x=nλ+Δx(n=0,1,2,…).
3 時間間隔與周期關系不確定導致多解
在波向前傳播的過程中,質點在各自平衡位置兩側做簡諧運動,由于簡諧運動具有周期性而出現多解.
例3一列簡諧橫波沿x軸正方向傳播,在t1=0和t2=0.2s時的波形分別如圖2中實線和虛線所示.已知該波的周期T>0.2s.下列說法正確的是( ).

圖2
A.波速一定為0.4m·s-1
B.振幅一定為0.04m
C.波長可能為0.08m
D.周期可能為0.8s
解析
因為t1=0和t2=0.2s時的波形分別如圖2中實線和虛線所示,二者至少相差半個周期,故
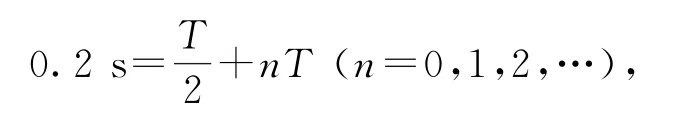
而T>0.2s,故周期T=0.4s,選項D錯誤.
由圖可知,波長為0.16m,故選項C錯誤.
由圖知振幅是0.02m,選項B錯誤.
點評
本題在t1=0和t2=0.2s時的波形正好步調相反,則有…),外加約束條件T>0.2s,多解變為唯一解.
4 雙多解
簡諧運動的時間具有周期性,可得周期的多解;機械波空間運動具有周期性,可得波長的多解;根據可得速度的雙多解.
例4如圖3是一根繃緊的水平繩,在繩上存在著相距14m的a點和b點,已知a點處于b點的左邊.現在繩中有一列簡諧波向右邊傳播.當a點在正向最大位移處的時候,b點正好在零位移處,并且向下方運動.1s之后,a點的位移變成0,向下運動,b點正好處于負向位移最大處.那么這列波的傳播速度可能為( ).
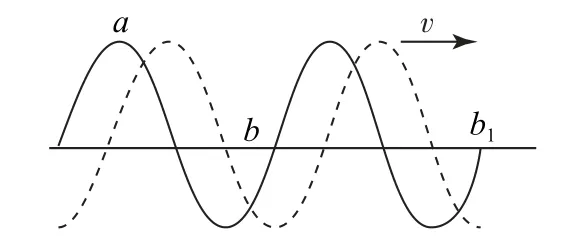
圖3
A.4.67m·s-1B.6m·s-1
C.10m·s-1D.14m·s-1
解析
由題意,實線為t=0時刻波形,虛線為t=1s時刻波形,根據題意,標出a、b點位置,b點位置還可以是距b點為波長整數倍的b1、b2等一系列的點,所以
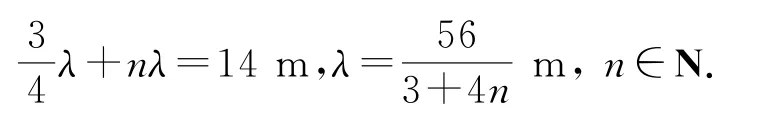
由于t可能大于周期T,所以
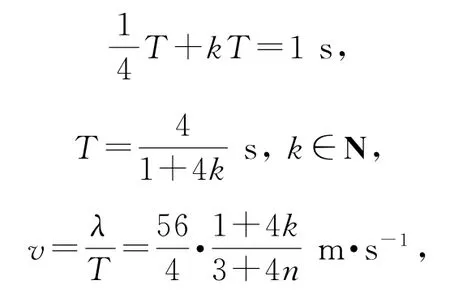
其中n和k分別是由波的概念和振動概念引出的自然數,二者是相互獨立的,無一一對應關系.通過嘗試可得,當n=0,k=0,選項A正確;當n=1,k=1時,選項C正確;其他選項n和k不可能同時為整數.
點評
通過嘗試,先取n=0,再將選項中的v代入公式,求k值,若k為整數,該選項正確.
質點振動nT(波傳播nλ)時,波形不變,在波的傳播方向上,當兩質點平衡位置間的距離為nλ(n=1,2,3,…)時,它們的振動步調總相同;當兩質點平衡位置間的距離為時,它們的振動步調總相反;對于一個確定的質點,每經過一個周期,振動重復出現,波的傳播可以雙向傳播.以上三點是形成機械波問題多解的原因.從形成原因出發,是解決這一類問題的關鍵.

