基于模糊規則學習的無監督異構領域自適應

孫 武，鄧趙紅,2,3+，婁瓊丹，顧 鑫，王士同

1.江南大學 人工智能與計算機學院，江蘇 無錫214122

2.復旦大學 計算神經科學與類腦智能教育部重點實驗室，上海200433

3.張江實驗室，上海200120

4.江蘇北方湖光光電有限公司，江蘇 無錫214000

傳統機器學習的前提是假設訓練集和測試集具有相同的特征空間和數據分布。然而，當兩個相關數據集的特征空間或數據分布存在差異時，傳統機器學習的訓練模型并不能得到滿意的效果。因此，解決此類問題的遷移學習被廣泛研究。隨著遷移學習的關注度越來越高，遷移學習在理論和實踐上都取得了很大的進步。領域自適應作為遷移學習的一個分支，在執行兩個相似任務的領域之間傳遞知識。根據特征空間的異同，領域自適應模型可以分為兩類：同構領域自適應和異構領域自適應。

同構領域自適應是為了解決源域和目標域之間特征維度相同但數據分布不同的問題。對于目標域中存在部分已標簽樣本的情況，Aytar 等人提出了一種基于模型的遷移支持向量機算法，Yang 等人提出了一種自適應支持向量機模型，與其相似的是Bergamo 等人也提出一種通過學習自適應支持向量機進行領域自適應的模型。上述幾種常見的同構領域自適應方法也被稱為半監督同構領域自適應模型。當目標域中都是無標簽實例時，具有代表性的模型有TCA（transfer component analysis）、JDA（joint distribution adaptation）和GFK（geodesic flow kernel）等。絕大部分的同構領域自適應模型的目標是最小化兩個域之間的分布差異。常見的跨域數據之間度量距離的方式有最大均值差異（maximum mean discrepancy，MMD）、Bregmann 距離、KL 距離和Wasserstein 距離等。

異構領域自適應是為了解決源域和目標域之間特征維度不同且數據分布不同的問題。相比于同構領域自適應模型，異構領域自適應模型的應用范圍更廣。HeMap（heterogeneous spectral mapping）利用光譜映射將源域數據和目標域數據投影到一個公共子空間，在保持源域和目標域原始數據結構的前提下最大化兩個域之間的相似性；DAMA（domain adaptation using manifold alignment）是一種流行對齊的方法，利用標簽信息將源域數據和目標域數據映射到一個公共子空間進行學習；ARC-t（asymmetric regularized cross-domain transfer）是一種基于度量學習的方法，通過訓練非對稱變換將一個域映射到核空間中對齊另一個域；HFA通過學習兩個特征變換矩陣，將源域數據和目標域數據分別映射到一個公共子空間，在保持原始特征結構的同時利用標準SVM 分類器進行學習；MMDT（max-margin domain transforms）對目標域數據學習一個線性變換矩陣來對齊源域，并同時優化變換矩陣和分類目標；CTSVM（correlation-transfer SVM）利用核CCA 對兩個域中的無標簽實例進行特征變換；ADMM（alternating direction method of multipliers）提出了一種基于稀疏特征變換的無監督方法；SFER（shared fuzzy equivalence relations）通過學習模糊等價關系提出了一種無監督異構領域自適應模型。因為異構領域自適應具有更廣的普適性，所以本文的重點是研究異構領域自適應。

然而，上述異構領域自適應模型大多數屬于半監督的方法，需要借助目標域中部分已標簽樣本來獲得良好的性能。為了拓展異構領域自適應在無監督方法上的應用，本文提出了一種新穎的基于TSK模糊系統（Takagi-Sugeno-Kang fuzzy system，TSK-FS）的無監督異構領域自適應算法（unsupervised heterogeneous domain adaptive with TSK-FS，FUHDA）。（1）本文通過TSK-FS 的模糊前件將源域數據和目標域數據分別映射到兩個特征隱空間。（2）本文通過訓練兩個后件參數矩陣將源域數據和目標域數據線性映射到同一個公共特征子空間。（3）線性判別分析（linear discriminant analysis，LDA）和主成分分析（principal component analysis，PCA）分別被用于減少源域數據和目標域數據因特征變換所造成的信息損失。為了最大化兩個域數據之間的相關性，本文還采用了典型相關性分析（canonical correlation analysis，CCA）作為約束項。（4）為了有效減少公共特征子空間中兩個域之間的分布差異，本文采用了一種比較流行的MMD 度量方法。為了驗證本文算法的有效性，本文將線性SVM 作為基準分類器，通過訓練公共特征子空間中的源域數據來測試目標域數據的標簽。

本文的主要貢獻歸納如下：

（1）提出了一種基于模糊規則學習的無監督異構領域自適應算法（FUHDA）。該算法通過TSK-FS的模糊前件將兩個域數據非線性映射到兩個特征隱空間，再學習兩個后件參數矩陣分別將源域特征隱空間數據和目標域特征隱空間數據線性映射到一個公共的特征子空間。

（2）采用了多種信息保持策略作為約束項來減少因特征變換所造成的信息損失，并且通過CCA 最大化兩個域數據之間的相關性。

（3）通過組織大量的實驗，證明了所提算法的有效性，實驗結果優于現有的異構領域自適應模型。

1 相關工作

1.1 領域自適應相關概念

1.2 TSK 模糊系統

TSK-FS 是一種基于模糊規則的推理系統。因為規則庫簡單且具有良好的學習能力，TSK-FS 已成功應用于許多遷移學習場景。在特征學習領域，TSK-FS 通過模糊規則將原始特征映射到新的特征空間。在含有條規則的TSK-FS 中，第條規則可定義為如下形式：

當前件參數確定時，TSK-FS 可以將原始特征投影到一個由模糊規則映射的新特征空間。進一步的，式（5）可表示為式（6）中的線性模型：

其中，x表示原始特征向量經過模糊規則映射得到的新特征向量，p表示后件參數向量。在已知x的前提下，p可通過最小二乘法解得。

2 基于TSK-FS 的無監督異構領域自適應

本章提出了一種新的基于模糊規則學習的無監督異構領域自適應方法，即FUHDA。FUHDA 從三方面對變換后的源域數據和目標域數據進行約束。（1）在公共特征空間內，最小化源域數據與目標域數據之間的分布差異；（2）在公共特征空間內，最大化源域數據與目標域數據之間的相關性；（3）在公共特征空間內，分別最小化源域數據與目標域數據的信息損失。因此，本文算法的目標公式可定義為式（8）。

其中，第一項表示變換后的源域與目標域之間的分布差異；第二項表示公共特征子空間中源域數據與目標域數據之間的相關性信息損失；第三項和第四項分別為源域和目標域特征變換后的信息損失。是一個多輸出的TSK-FS。

2.1 公共特征子空間的構造

公共特征子空間的構建是學習式（8）的基礎。圖1 展示了FUHDA 特征變換的具體過程。首先，FUHDA 采用兩個TSK-FS。經過模糊前件非線性映射，源域和目標域數據分別被映射到兩個特征隱空間。然后，FUHDA 訓練兩個后件參數矩陣分別將源域隱空間特征和目標域隱空間特征線性映射到同一個公共特征子空間。具體映射過程被定義如下。

圖1 基于TSK-FS 的特征變換Fig.1 Feature transformation based on TSK-FS

其中，和分別表示源域數據和目標域數據經過TSK-FS 前件參數映射所得到的新特征。和分別表示多輸出TSK-FS 的維后件參數矩陣。則樣本x和x經過TSK-FS 特征變換后的輸出為式（10a）和式（10b）。

則對于源域數據和目標域數據中的所有樣本，經特征變換到公共特征子空間后，可表示為：

需要注意的是，本算法中源域和目標域使用的是兩個TSK-FS，因此后件參數和是兩個不同的變換矩陣，并且前件參數采用了一種確定性的聚類算法Var-Part分別進行計算。

2.2 分布差異最小化

為了有效地降低源域數據和目標域數據之間的分布差異，本文算法引入最小化邊緣分布差異和條件分布差異這兩個策略。

首先，本文采用MMD 算法來度量公共特征子空間中源域數據和目標域數據之間的邊緣分布差異。MMD 是領域自適應中應用最廣泛的距離度量方法，該方法通過映射函數將原始數據映射到再生核希爾伯特空間（reproducing kernel Hilbert space，RKHS）。MMD 通過計算兩類分布不同的樣本在上的均值差，來判斷這兩類數據分布之間的差異程度。根據式（10）所構造的映射函數，MMD 函數具體如下：

其次，本文采用Long 等人提出的聯合分布差異度量方法JDA。該算法利用源域訓練的分類器來預測目標域數據，再將預測標簽作為目標域偽標簽來表示目標域中的類條件分布。通過對偽標簽進行迭代更新，該算法能夠進一步減小兩個領域之間條件分布的差異。因此，本文最小化領域之間條件分布差異的公式可具體如下所示：

通過綜合邊緣分布差異和條件分布差異這兩個角度來最小化源域數據與目標域數據之間的分布差異，則目標式（8）中的第一項即為：

2.3 領域相關性最大化

CCA 是一種常用的降維算法，該算法能夠有效度量兩組數據之間的相關性，為了有效地最大化源域和目標域數據的相關性，本文采用了CCA 算法作為約束項。這里將式（7e）中的和作為CCA 中的一組投影向量，則CCA的目標函數可以表示如下：

其中，=-(1/)11(==)為中心化矩陣，1 ∈R是元素全為1 的列向量。為了將兩個領域數據投影到維空間，將、拓展為式（9e）和式（9f）中的投影矩陣、。因為投影向量的縮放不會影響式（15）中的最優解，所以可將式（14）中的目標函數優化為如下形式：

其中，式（16）中的約束條件作用是限制投影矩陣的大小從而優化其方向。為了同時優化投影矩陣和，可以將式（16）重新定義為式（17）。

2.4 源域判別信息保持

LDA 算法是一種有監督的數據降維方法，該方法通過尋找最優的投影方向使得同類的樣本之間距離更近，不同類的樣本之間距離更遠，同時還能最大化保持原始樣本的信息，因此本文采用LDA 算法作為約束項來保持源域數據的判別信息。LDA 的具體優化公式如下：

其中，叫作類間散度矩陣，叫作類內散度矩陣，兩者的具體定義如下：

2.5 目標域結構信息保持

因為目標域數據沒有標簽，所以為了有效地保持目標域數據在特征映射后的結構信息，本文通過最大化目標域數據在映射子空間的方差進行約束。因此，該約束項的目標函數可以表示如下：

2.6 目標函數優化

其中，、、、為權衡參數，用來平衡每項的重要性。式（24）中還通過最小化tr()來防止過擬合。注意，式（24）不因的縮放而影響最終優化結果，因此，目標函數可以重寫為式（25）：

對式（25）使用拉格朗日函數可得：

令?/?=0，則有：

其中，=diag(,,…,?)是含有個特征值的對角矩陣，一般可通過廣義特征值分解進行求解。

根據上述公式推導過程，本文算法的具體偽代碼如算法1 所示。

FUHDA

輸出：目標域數據的預測標簽。

1.根據式（2）、式（3）、式（4）、式（7）和式（9）得到兩個隱空間數據和；

2.計算式（14c）、式（18）、式（21）和式（23）中的、、、和；

3.for=1,2,…,do

4.根據式（14d）更新M；

5.求解式（27），得到，根據獲得變換和；

6.根據式（11a）和式（11b）更新和；

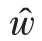
8.end for

3 實驗結果和分析

3.1 數據集

為了充分驗證本文算法的有效性，本文選取了Office-Caltech 數據集、Wiki 數據集和Reuters 數據集進行了實驗驗證，每個數據集的具體信息如表1所示。

表1 數據集的統計信息Table 1 Statistical information of datasets

Office-Caltech 由Office-31 數據集和Caltech-256數據集組成，是一個視覺目標識別數據集，該數據集包括4個子數據集：A(Amazon)、D(DSLR)、W(Webcam)和C(Caltech)。這4 個子數據集均具有相同的10 種標簽類別，其中A、D 和W 來自Office-31 數據集，C 來自Caltech-256 數據集。在Office-Caltech 數據集的4個子數據集A、D、W 和C 中，每個子數據集可被劃分為兩個領域（即SURF（800 維）和DeCAF6（4 096維）），分別作為源域和目標域（或目標域和源域）。因此，該數據集可構造8 個遷移任務。

Wiki 數據集是一個文本圖像數據集，每個樣本都包含了一個圖像和其對應的文本描述。這里使用SIFT（scale-invariant feature transform）特征提取方法將圖片特征降低到128 維，使用LDA 方法將文本特征降低到10 維。本文把圖像和文本領域作為源域和目標域（或目標域和源域），因此，可構造2 個遷移任務。

Reuters 是一個跨語言文本數據集，該數據集中包含了18 758 篇文章，分別選自5 種語言（English、French、German、Italian、Spanish）的6 個類別。本文將English、French、German 和Italian 4 個視角的數據作為源域，Spanish 視角的數據作為目標域。因此，可構造4 個遷移任務。

3.2 實驗設置

實驗中，本文算法將與6 個對比算法進行比較。其中，Linear CCA、CTSVM、CDLS 是已有的異構遷移學習算法；算法FUHDA-noCCA 是去除CCA 數據相關性約束項所形成的對比算法，用于驗證最大化數據之間相關性的有效性；對于算法FUHDA-noSP和FUHDA-noTP，它們是分別去除源域和目標域的信息保持項所形成的對比算法，用于驗證信息保持項的有效性。本文將線性SVM 作為基準分類器來檢驗算法的遷移效果。本文將6 個算法的公共子空間特征維度都設置為100，其他參數設置具體如表2所示。

表2 算法的參數設置Table 2 Parameter settings of algorithms

對比算法的簡要介紹如下：

LinearCCA：該算法用線性CCA 對源域和目標域中的實例進行建模，得到一個公共的特征空間。

CTSVM：該算法是一個簡化核CCA 方法，通過優化核CCA 對源域和目標域中的實例進行學習，得到一個公共的特征空間。

CDLS：該算法獲得一個領域不變的公共子空間，并且學習具有代表性的跨域標記，以達到異構領域自適應的目的。

FUHDA-noCCA：該方法是所提算法的一種變型，去除了CCA 數據相關性約束項。

FUHDA-noSP：該方法是所提算法的一種變型，去除了源域數據的結構信息保持項。

FUHDA-noTP：該方法是所提算法的一種變型，去除了目標域數據的判別信息保持項。

3.3 實驗結果分析

本文算法與6 個對比算法在14 個遷移任務中的實驗結果具體如表3、表4 和表5 所示。

表4 各算法在Wiki數據集上的準確度Table 4 Accuracy of algorithms on Wiki dataset %

表5 各算法在Reuters數據集上的準確度Table 5 Accuracy of algorithms on Reuters dataset %

由表3 可知，在Office-Caltech 數據集的8 個任務中，所提算法在7 個任務中表現最好，在另外1 個任務中也達到次優的效果。在平均精度上，所提算法與其他對比算法相比也是最優的。對于算法Linear-CCA 和CTSVM，它們只對數據進行特征變換，而沒有考慮特征變換所造成的信息損失，因此遷移效果較差。另外，通過與FUHDA-noCCA、FUHDA-noSP和FUHDA-noTP 進行對比分析，證明了本文考慮利用CCA 最大化數據之間的相關性，并且同時引入源域判別信息保持策略和目標域結構信息保持策略的優越性。

表3 各算法在Office-Caltech 數據集上的準確度Table 3 Accuracy of algorithms on Office-Caltech dataset %

由表4 可知，在Wiki 數據集的2 個任務中，所提算法均優于其他對比算法。

由表5 可知，在Reuters 數據集的4 個任務中，所提算法在3 個任務中表現最好，且平均精度在所有任務中也是最好的。

綜上所述，本文算法在異構領域自適應任務中能夠取得優異的結果，并且證明了相關性約束和多種信息保持策略的有效性。

3.4 參數分析

本節將從Office-Caltech 數據集和Wiki數據集的10 個領域自適應任務中分析算法的收斂性，以及模糊系統的規則數，權衡參數、和對算法準確度的影響。

分析圖2 可知，隨著規則數的增加，大部分領域自適應任務所獲得精度呈現出一種平緩波動的趨勢，只有少部分領域自適應任務的精度波動較大。值得注意的是，隨著規則數的增加，模型的計算復雜度是呈指數級增長的。而從圖2 可以看出，在規則數為3 時，所有任務都能獲得較好的效果。因此，綜合考慮模型復雜度和算法的性能，本文將模糊系統的規則數設置為3 是合理的。

圖2 規則數分析Fig.2 Rule number analysis

圖3 展示了10 個領域自適應任務在不同迭代次數下的精度。從圖中可以看出，當迭代次數超過6 次時，所有任務的精度趨于穩定。因此，本文實驗中將迭代次數設為15 是合理的，并且證明了所提算法具有良好的收斂性。

圖3 收斂性分析Fig.3 Convergence analysis

圖4 分別展示了在固定其他參數時，改變某一權衡參數、或對實驗效果的影響。從圖4（a）和圖4（b）可以看出，當=2或=2時，大部分任務都能取得一個最優的精度。對于參數，從圖4（c）可知，所有任務在區間(2,2)內都能取得較好的精度。

圖4 參數敏感性分析Fig.4 Parameter sensitivity analysis

4 結論和展望

本文提出了一種新穎的無監督異構領域自適應算法FUHDA。首先，FUHDA 通過模糊前件的非線性變換將源域數據和目標域數據分別映射到兩個特征隱空間。然后，FUHDA 訓練兩個后件參數矩陣將源域和目標域線性映射到同一個公共特征子空間。為了降低兩個域數據之間的分布差異，FUHDA 將最大化兩個域數據之間的相關性和相關信息保持策略作為約束項，有效地減少了因特征變換所造成的信息損失，同時也提升了算法的領域自適應能力。通過實驗分析，證明了所提算法的優越性。但是，算法還存在一定的改進空間，比如FUHDA 在處理高維數據時，因為TSK-FS 的引入使計算復雜度變高，未來將致力于改進TSK-FS 使算法的計算復雜度降低。