俯沖帶庫侖楔形體力學

胡巖

1 中國科學技術大學地球和空間科學學院，合肥 230026 2 中國科學技術大學蒙城地球物理國家野外科學觀測研究站，安徽蒙城 233527 3 中國科學院比較行星學卓越創新中心, 合肥 230026

0 引言

楔形體理論主要研究剖面呈三角形的地質塊體受力狀態.從山前推覆構造到俯沖帶弧前增生楔，楔形體普遍存在.然而如何描述楔形體內部應力狀態，進而分析楔形體內部變形(破裂過程)和巖石性質以及斷層強度之間的關系，一直是地學研究關注的問題.針對不同楔形體材料以及邊界條件人們先后提出多個應力解析解(例如，Davis et al., 1983; Dahlen, 1984, 1990; Dahlen et al.，1984; Liu and Ranalli, 1992; Platt, 1993；Yin, 1993, 1994; Williams et al., 1994；Yin and Kelty, 2000).這些解析解均假設靜力平衡條件，而忽略慣性力項.雖然考慮慣性力項和其他復雜性(例如復雜材料性質及其不均一性，底部邊界摩擦性質不均一性等)的模型可以更真實地模擬俯沖帶增生和剝蝕過程，但是求解過程耗時并且難以獲得解析解.本文首先簡要介紹部分已發表的應力解析解，然后詳細介紹基于理想彈塑性楔形體的應力函數解析解(Hu and Wang，2006).最后介紹基于該解析解提出的動態庫侖楔形體理論(Wang and Hu，2006).

1 楔形體應力解析解

1.1 彈性楔

Yin(1993,1994)研究了剖面為三角形的彈性楔形體內部應力狀態(圖1a).該楔形體底部為靜態摩擦邊界，有效摩擦系數為μ′b.在左邊界垂直于表面的壓力隨深度線性增加.楔形體上表面為自由空氣界面.Yin和Kelty(2000)進一步研究了這個三角形楔形體，假設左邊界壓力變化為深度的二次函數.具體推導解析解過程請參考Yin和Kelty(2000)，這里介紹該文章得出的最終解.

+(1-λ)ρwgsinαx,

(1)

(2)

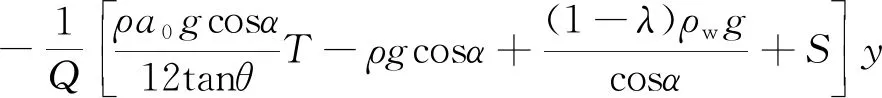
(3)

其中，α和β分別為上表面坡度角和下表面的傾角，θ=α+β，σx和σy分別為x和y方向的正應力(本文中，壓應力為負，拉張應力為正)，τxy為剪應力，ρw和ρ分別為水和巖石的密度，g為重力加速度，以及如下關系式：

(4)

其中，Xe和Ye分別為重力和孔隙流體產生的x和y方向的體力，l=-sinθ,m=cosθ.Yin和Kelty(2000)通過以上應力解析解很好的解釋了美國夏威夷毛納洛基拉韋厄裂谷地區(Mauna Loa-Kilauea)正斷層和逆沖斷層共同存在的現象，然而該解析解比較復雜，難以方便地應用.

Liu和Ranalli(1992)研究了梯形形狀的彈性楔形體內部應力狀態.不同于Yin和Kelty(2000)只有左側邊界施加外力，該楔形體左右邊界壓力均為深度的二次函數.其他邊界條件以及推導過程和Yin和Kelty(2000)類似，但是得出的解析解比(1)—(4)更復雜.因為篇幅有限，本文不再累述.

圖1 楔形體應力解析解和海溝增生楔地震反射剖面[(a) 修改自Yin and Kelty(2000)圖3.(b)來自Hu and Wang (2006)圖1b.(c)來自Wang and Hu (2006)圖2a](a)有限長(X0)彈性三角形楔形體(Yin, 1993,1994; Yin and Kelty, 2000).左邊界壓力Fx為深度的函數.底部為靜態摩擦邊界.(b)無限長理想彈塑性楔形體(Hu and Wang, 2006).其中α和β分別為上表面坡度角和下表面傾角，ρw和ρ分別為水和巖石的密度，g為重力加速度.σn和τn分別為下表面正應力和剪應力.(c)日本南海海溝地震反射剖面(Park et al., 2002).Fig.1 Analytical stress solutions in the wedge and a seismic reflection profile in an accretionary prism [(a) Modified from Fig.3 in Yin and Kelty (2000). (b) From Fig.1b in Hu and Wang (2006). (c) From Fig.2a in Wang and Hu (2006)](a) An elastic triangle-shaped wedge with a limited length (X0) (Yin, 1993,1994; Yin and Kelty, 2000).The external force Fx normal to the left boundary is a function of the depth. A static friction law is applied to the lower boundary. (b) Elastic perfectly-plastic wedge with infinite length (Hu and Wang, 2006). α and β represent the surface slope angle and basal dipping angle, respectively. ρw and ρ represent the water and rock density, respectively. g is the gravitational acceleration. σn and τn represent the normal and shear stress at the lower boundary. (c) Seismic reflection profile in the Nakai trough in Japan (Park et al., 2002).

1.2 臨界理想塑性楔

從20世紀80年代開始，研究者先后發表了多篇文章討論楔形體(圖1b)在臨界破裂條件下應力狀態(Davis et al., 1983; Dahlen, 1984，1990; Dahlen et al., 1984; Zhao et al., 1986; Breen and Orange, 1992; Willett et al., 1993; Wang and Davis, 1996).經典臨界楔形體理論描述了理想庫侖塑性楔形體應力狀態.庫侖破裂準則定義了楔形體產生塑性破壞的應力屈服條件.應力在屈服面上時楔形體處于臨界破裂狀態.當實際應力小于屈服應力，楔形體處于彈性穩定狀態；當應力大于屈服應力，楔形體則處于破壞失穩狀態.

本文主要介紹Dahlen(1984)推導的經典臨界楔形體理論.楔形體邊界條件和1.1節介紹的彈性楔形體類似.楔形體內部孔隙水壓P基于Hubbert-Rubey流體壓力比定義如下(Davis et al., 1983)：

(5)

其中λ為孔隙流體壓力比，D為水深.底部邊界滿足靜態摩擦條件τn=-μ′b(σn+P)，其中μ′b為有效摩擦系數，σn和τn分別為底部正應力和剪應力.如果楔形體為均一庫侖塑性材料并且內聚力S0為深度的函數，我們可以得到：

S0=η(1-λ)μρgycosα,

(6)

其中η為無量綱常數，μ=tanφ為楔形體內摩擦系數，φ為內摩擦角.基于應力摩爾圓(圖2)，應力和角度滿足以下關系：

圖2 臨界破裂狀態下楔形體應力摩爾圓σ1和σ3分別為最大和最小主壓應力，φ為內摩擦角，ψc為最大主壓應力和上表面的夾角，r為摩爾圓半徑.Fig.2 Mohr circle of a critical wedge on the verge of failureσ1 and σ3 represent the maximum and minimum principal compressional stress. φ represents the internal friction angle. ψcrepresents the angle between the maximum principal compressional stress and the surface. r is the radius of the Mohr circle.

(7)

(8)

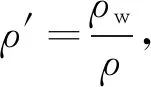
(9)

ψc由(10)式計算得到：

(10)

(11)

以Dahlen(1984)文中的楔形體為例，該楔形體幾何形狀為地表坡度α=4°,底部邊界傾角β=4.2°.需要說明的是，地殼巖石的內摩擦系數μ一般小于1.由于經典臨界楔形體相關文章(例如，Davis et al., 1983; Dahlen, 1984)均采用μ=1.1.為了更方便讀者對比經典解析解和下文介紹的應力解析解，這里也假設μ=1.1.具體選取什么內摩擦系數不會影響本文的結論.假設孔隙流體壓力比λ=0.8，則當底部邊界有效摩擦系數為μ′b=0.17時，該楔形體處于擠壓型臨界狀態(圖3a).楔形體最大主壓應力呈近水平狀態，可能產生逆沖型破裂(圖3a虛線表示可能的破裂方向).當μ′b減小后，楔形體進入穩定狀態.這時解析解(8)式不再適用.只有當μ′b=0.017時(圖3e)，楔形體主壓應力呈近垂直狀態.楔形體達到拉張型臨界破裂狀態，其內部應力可以被(8)式描述.這時楔形體可能產生拉張型正斷層(圖3e虛線示意可能的正斷層破裂方向).當μ′b大于0.17或者小于0.017時，楔形體處于破裂失穩狀態，解析解(8)式亦不適用.

Hu和Wang(2008)測量了22個俯沖帶弧前幾何形狀.根據經典塑性臨界楔形體理論，Hu 和 Wang(2008)認為這些俯沖帶大都處于穩定狀態，即解析解(8)式并不適用于解釋這些俯沖帶弧前應力狀態.如果假設更軟(例如，更小的μ和更高的λ)的楔形體巖石，一些增生楔處于臨界拉張型破裂狀態，和俯沖帶擠壓型區域應力環境不一致.這表明經典臨界楔形體理論需要進一步完善以更好地解釋俯沖帶弧前幾何形狀和構造應力特征.

圖3 楔形體內部應力狀態隨底部有效摩擦系數變化圖[修改自Wang and Hu(2006)圖7]楔形體參數α=4°,β=4.2°,μ=1.1,λ=0.8保持不變，底部有效摩擦系數μ′b逐漸減小.(a)臨界擠壓型破裂狀態，μ′b=0.17.黑色成對箭頭為最大和最小主壓應力.虛線為可能的破裂方向.(b)擠壓型穩定狀態，μ′b=0.1.(c)中性穩定狀態，μ′b=0.038.最大和最小主壓應力和楔形體上表面夾角為45°.(d)拉張型穩定狀態，μ′b=0.028.(e)臨界拉張型破裂狀態，μ′b=0.017.Fig.3 Stress status in a wedge with a varying basal effective frictional coefficient [Modified from Fig.7 in Wang and Hu (2006)]In this wedge, we keep α=4°,β=4.2°,μ=1.1,λ=0.8 and vary the basal effective frictional coefficient. (a) Compressively critical state. Black paired arrows represent the maximum and minimum principal compressional stresses. Dashed lines represent potential faulting directions. (b) Compressively stable state, μ′b=0.1. (c) Neutral stable state, μ′b=0.038. The angle between the maximum (or minimum) principal compressional stress and the surface is 45°. (d) Extensionally stable state, μ′b=0.028. (e) Extensionally critical state, μ′b=0.017.

2 理想彈塑性楔形體應力解析解

當楔形體處于臨界破裂狀態時，內部應力同時滿足庫侖破裂條件和彈性虎克定律.Hu和Wang(2006)研究理想彈塑性楔形體材料并且得到應力函數解析解.該解析解不僅適用于處于臨界破裂狀態的楔形體，而且適用于穩定狀態的楔形體.本文介紹該解析解推導過程.

對于圖1b所示楔形體，假設應力函數Φ為：

(12)

其中ki(i=1,2,3,4)為待解參數.則楔形體各邊界條件如下.

自由表面滿足：

(13)

(14)

應力各分量表達式如下：

(15)

將(12)式代入(15)式，得到應力表達式如下：

(16)

基于邊界力和內部應力關系(王仁等,1979)，可以得到：

(17)

(18)

將(15)式代入(13)式，得到k1=0，k3=ρ′sinα.綜合(5)，(14)，(16)，(17)式和(18)式，可以得到：

(19)

從而可以解出k2和k4分別為：

(20)

(21)

其中

(22)

因此常數a不是一個自由變量，而是和楔形體形狀、孔隙流體壓力比以及底部摩擦系數有關.基于(21)式，應力分量可以寫為：

(23)

比較(8)式和(23)式，當m=mc時，則(23)式和經典臨界楔形體解析解完全一致，亦即經典臨界楔形體解析解為彈塑性楔形體解析解(23)式的子集.

對于1.2節給出的楔形體例子，當μ′b=0.17或者μ′b=0.017時，m=mc，這時解析解(23)式可以描述楔形體分別處于臨界擠壓型破裂和臨界拉張型破裂狀態時的應力分布(圖3a和圖3e).當μ′b=0.1時，楔形體為擠壓型穩定狀態，解析解(23)式亦能給出應力分布(圖3b).當μ′b=0.038時，楔形體為中性穩定狀態，最大和最小主應力與楔形體表面夾角為45°(圖3c).當μ′b=0.028時，楔形體為拉張型穩定狀態(圖3d).

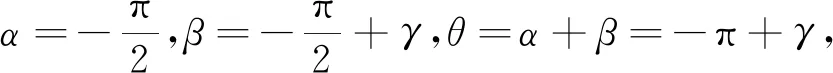
圖4 (a)大壩和(b)三角形懸臂梁受力示意圖ρw和ρ分別代表水和巖石的密度.g為重力加速度.γ為三角形楔形體夾角.Fig.4 Illustration of the stress status in (a) a dam and (b) a triangle-shaped hanging beamρw and ρ represent the water and rock density, respectively. g is the gravitational acceleration. γ is the angle of the triangle-shaped wedge.

(24)

(24)式與徐芝綸(1979，第58頁)給出的解析解一致.

圖4b給出懸臂梁的受力示意圖.對于該例子，α=0,β=γ,θ=α+β=γ，其中γ為三角形懸臂梁夾角.代入該幾何參數可以得到：

(25)

該解析解(25)式與徐芝綸(1979，第67頁)給出的解析解一致.

3 動態庫侖楔形體理論

弧前增生楔和侵蝕前緣在地震周期的應力演化及其與俯沖界面摩擦性質的關系一直是地學研究的熱點問題.雖然不同俯沖帶前緣幾何形狀各不相同，但是總體來說可以分為兩部分.以日本南海海溝為例(圖1c)(Park et al., 2002)，在俯沖帶前緣靠近海溝部分，地震反射剖面顯示該部分楔形體發育大量逆沖斷層，表明經常產生永久變形，同時地表坡度也比較陡.我們把這部分楔形體稱為外部楔形體(Outer wedge).在更靠近內陸部分，楔形體內部缺少強烈的構造活動，該地區沉積層沒有被破壞而呈較好的水平分布，其地表坡度角也比較小.我們把這部分楔形體稱為內部楔形體(Inner wedge).類似弧前幾何形狀和構造特征也存在于其他俯沖帶，例如，卡斯卡迪亞(Cascadia)(McNeill et al., 1997；Gulick et al., 1998)，阿拉斯加(von Huene and Klaeschen, 1999; von Huene and Raneo, 2003)，莫克蘭(Makran)(Kopp et al., 2000；Kukowski et al., 2001)，東北日本(von Huene et al., 1986，1994)，秘魯(Krabbenh?ft et al., 2004)，湯加(von Huene and Scholl, 1991)等.在部分俯沖帶，外部和內部楔形體地表坡度角可能不如日本南海海溝(圖1c)差異那么大，但是構造差異特征幾乎存在于每一個俯沖帶前緣.例如在阿留申俯沖帶，外部和內部楔形體地表坡度角只相差1°，但是幾乎所有的永久變形都發生在靠近海溝近35 km寬度的外部楔形體，而更遠離海溝區域35 km寬的內部楔形體幾乎沒有永久變形(Bruns and von Huene，1986；Scholl et al., 1986).

除了弧前楔形體內部構造特征顯著不同，一般認為俯沖界面摩擦性質也具有不均一性.俯沖帶斷層面可能存在大小形狀不一的凹凸體(Bilek and Lay, 2002).凹凸體接觸面為黏滑，可以積累應力，孕育地震.凹凸體之間斷層面可能為蠕滑，不孕育地震.部分區域可能表現為有條件蠕滑.這些摩擦性質可以用含速率與狀態的摩擦(Dieterich，1994；Ruina，1983)描述.總體來說，從海溝沿俯沖界面到深部可以分為三部分(Hu and Wang，2008).在淺部，由于巖石固結程度比較低，這部分斷層表現為速度強化.中間部分為生震帶，摩擦性質為速度弱化.更深部分由于高溫高壓條件巖石主要為黏性變形，主要表現為蠕滑.

如何解釋弧前構造特征的這些差異性？Byrne等(1988)認為這些構造差異性是由楔形體材料強度不同決定的.內部楔形體結晶基底作為支柱阻礙前緣因為俯沖效應導致的縮短，從而變形主要發生在巖石固結程度低、強度小的外部楔形體.這個理論可以較好地解釋部分具有增生楔的俯沖帶，但是部分俯沖帶(例如阿拉斯加和日本南海海溝)缺少結晶基底或者結晶基底在更靠近內陸方向，該理論則不適用.Kopp和Kukowski(2003)進一步提出巖石固結程度更高、強度更大的沉積巖可以替代結晶基底，同樣充當支柱阻礙前緣的永久變形.然而大量研究表明弧前巖石強度和性質的差異可能并不是很大(Lallemand et al.，1994).這些研究只是關注弧前巖石性質的差異而忽略了斷層面摩擦性質的差異.

Wang和Hu(2006)提出動態庫侖楔形體理論，較好地解釋了弧前構造特征以及斷層面摩擦性質的差異性.該理論認為外部楔形體對應的底部邊界為無震蠕滑帶，摩擦性質為速度強化，而內部楔形體對應的底部邊界為斷層面生震帶，摩擦性質為速度弱化.地震發生時，內部楔形體底部邊界(生震帶)應力降低，摩擦系數減小，楔形體內部經歷彈性變形.而外部楔形體底部邊界由于速度強化，摩擦系數增加，同時深部生震帶同震向上擠壓可能導致楔形體孔隙流體壓力比升高.綜合效應可能導致外部楔形體達到擠壓型破裂狀態，產生永久變形.

我們以日本南海海溝(圖1c)為例進一步解釋該理論.基于Wang 和 Hu (2006)，內部楔形體幾何形狀為α=0.1°,β=9.5°.根據地震反射剖面共軛斷層夾角信息，設定內摩擦系數μ=0.7(Wang and Hu，2006).假設孔隙流體壓力比λ=0.5，則最大主壓應力和上表面的夾角ψ0隨底部邊界摩擦系數變化而變化(圖5b).由于內部楔形體底部邊界為生震帶，摩擦性質為速度弱化，在地震發生前摩擦系數應該比較低，例如μ′b=0.04.地震發生時，因為速度弱化，斷層面摩擦系數降低.假設內聚力系數η=0，則內部楔形體底部摩擦系數沿圖5b中黑色虛線向左側移動，這導致ψ0逐漸增加，即內部楔形體由中性穩定狀態(類似圖3c)逐漸變為拉張型穩定狀態(類似圖3d).由于底部摩擦系數實際不可能成為負數，因此內部楔形體永遠不可能到達虛線左側的端點(臨界拉張型破裂).地震發生后，由于斷層面不再滑動，基于速度弱化摩擦性質，底部斷層摩擦系數逐漸增加到地震前穩定狀態.如果內部楔形體內聚力系數更高，例如η=0.6，則內部楔形體在地震時更難達到臨界破裂狀態(圖5b灰色實線).因此在整個地震周期，內部楔形體只是在中性狀態和拉張型穩定狀態間轉換，只產生彈性變形，不會產生永久變形.

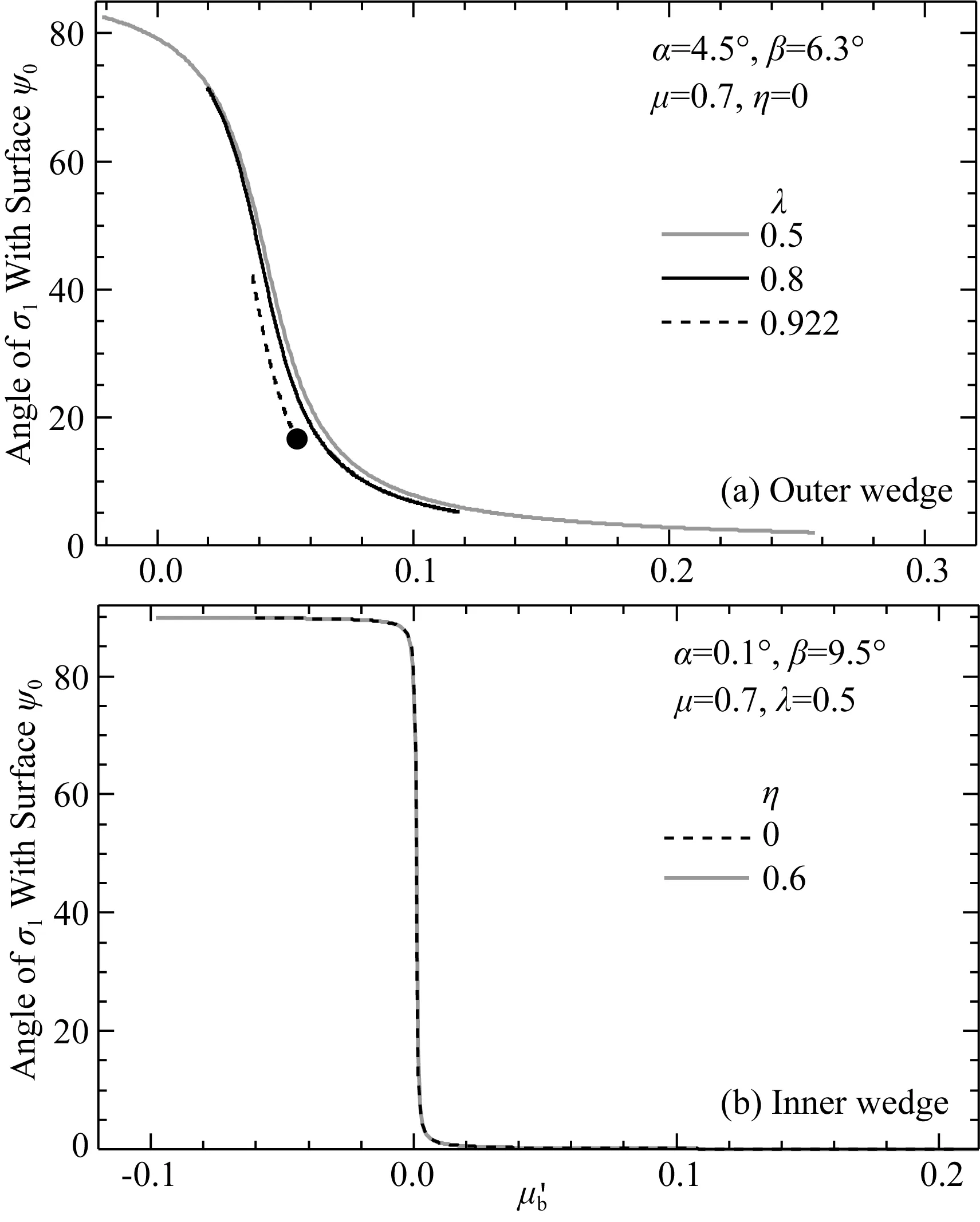
圖5 外部和內部楔形體地震周期應力演化[(a)修改自Wang and Hu(2006)圖9a.(b)修改自Wang and Hu (2006)圖11a](a)外部楔形體應力演化.楔形體參數α=4.5°,β=6.3°,μ=0.7,η=0保持不變.灰色實線、黑色實線和黑色虛線分別表示孔隙流體壓力比λ=0.5,0.8,0.922.(b)內部楔形體應力演化.楔形體參數α=0.1°,β=9.5°,μ=0.7,λ=0.5保持不變.黑色虛線和灰色實線分別表示內聚力常數η=0,0.6.Fig.5 Earthquake-cycle stress evolution in an outer wedge and an inner wedge [(a) Modified from Fig.9a in Wang and Hu (2006). (b) Modified from Fig.11a in Wang and Hu (2006)](a) Stress evolution in an outer wedge. The wedge parameters α=4.5°,β=6.3°,μ=0.7,η=0 keep constant. The gray solid line, black solid line and black dashed line represent λ=0.5,0.8,0.922, respectively. (b) Stress evolution in an inner wedge. The parameters α=0.1°,β=9.5°,μ=0.7,λ=0.5 keep constant. The black dashed line and gray solid line represent the cohesion constant η=0,0.6, respectively.

圖6 弧前外部和內部楔形體地震周期應力演化[修改自Wang and Hu (2006)圖12](a) 同震時弧前應力分布; (b) 震后弧前應力隨孔隙流體壓力比以及底部摩擦系數變化; (c) 震間(地震周期中后期)弧前應力狀態.Fig.6 The earthquake-cycle stress evolution of the outer and inner wedge in a forearc [Modified from Fig.12 in Wang and Hu (2006)](a) Coseismic stress status in the forearc; (b) Postseismic stress status depending on the changed pore fluid pressure ratio and basal frictional coefficient; (c) Interseismic (middle and late stages in an earthquake cycle) stress status in the forearc.

外部楔形體巖石固結程度相對較低，因此孔隙流體壓力比容易受應力條件改變而發生變化.我們假設η=0.由于外部楔形體底部為蠕滑帶，摩擦性質為速度強化，地震發生后斷層面摩擦系數增加.如果楔形體孔隙流體壓力比λ=0.5，則外部楔形體底部摩擦系數沿圖5a灰色實線向右側移動.當μ′b=0.26，外部楔形體達到臨界擠壓型破裂狀態(圖5a中灰色實線右側端點).在此條件下，底部摩擦系數需要增加Δμ′b=0.22.通常底部摩擦系數在地震時可能不會變化那么多.生震帶同震滑動不僅導致外部楔形體底部摩擦系數增加，更會擠壓外部楔形體，導致孔隙度減少，孔隙流體壓力增加，相應增加孔隙流體壓力比.如果λ=0.8，則底部摩擦系數只需要增加Δμ′b=0.08就可以達到臨界擠壓型破裂狀態(圖5a黑色實線右側端點μ′b=0.12).如果地震導致孔隙流體壓力比達到λ=0.922，當楔形體底部摩擦系數達到μ′b=0.047，亦即相對于震前只需稍微增加Δμ′b=0.007，外部楔形體即達到擠壓型臨界破裂狀態(圖5a黑色虛線右側端點).該狀態也是底部侵蝕狀態(圖5a黑色圓點)，即破裂面平行于下表面，外部楔形體底部物質將被不斷剝蝕隨著俯沖向深部帶入.相對于內部楔形體，較大震級地震就可以使得外部楔形體達到臨界擠壓型破裂.這很好地解釋了外部楔形體大量發育永久變形.

圖6進一步闡明弧前應力狀態在地震周期的演化.地震發生時(圖6a)，生震帶摩擦系數降到近似零，內部楔形體仍為穩定狀態，產生中性/拉張型彈性變形.而外部楔形體底部因為速度強化，底部摩擦系數增加到0.12，同時內部孔隙流體壓力比λ增加到0.8，楔形體達到臨界擠壓型破裂.地震以后，生震帶逐步積累應力，其摩擦系數亦逐步增加至地震前狀態(例如圖6b中μ′b=0.02).內部楔形體逐漸由中性穩定狀態變為擠壓型穩定狀態.而外部楔形體由于孔隙度逐漸恢復，λ逐漸減小，其底部摩擦系數因為速度強化而逐漸減少，內部應力狀態由地震時臨界擠壓型破裂恢復到擠壓型穩定狀態(圖6b).震后足夠長時間以后，弧前恢復到震前狀態，底部邊界摩擦系數均比較小，外部楔形體內部應力狀態呈近中性分布，內部楔形體呈擠壓型穩定狀態(圖6c).

外部和內部楔形體底部界面不同摩擦性質可能反映巖石性質的差異.在淺部由于巖石固結程度比較低、孔隙水壓比較高等原因，斷層性質表現為速度強化.而深部由于更高的溫壓條件和俯沖脫水過程，巖石固結程度高、孔隙水壓比較低，斷層從而表現為速度弱化.斷層面這種性質的差異性已經被比較廣泛的認可，例如Bilek和Lay(2002)指出斷層面由淺到深孕震性質這種差異性.

俯沖帶生震帶位置是地學研究的重要基本問題，對地震災害性評估具有重要的作用.基于實驗室巖石含速率與狀態的摩擦性質分析，生震帶淺部邊界由100～150 ℃巖石溫度控制，其深部邊界由350～400 ℃溫度控制(Hyndman and Wang, 1993; Oleskevich et al., 1999; Moore and Saffer, 2001).在這兩個溫度范圍之外，斷層面摩擦性質為速度強化，表現為蠕滑.然而對于缺少地表熱流觀測值的俯沖帶，難以獲取其熱結構參數，此外地表熱流較難以測量.動態庫侖楔形體理論提供了一個較方便可靠的辦法約束生震帶淺部邊界，即外部和內部楔形體的交匯處.

Wang等(2019)通過對比東北日本弧前地震震源機制解(例如，Hasegawa et al., 2012; Nakamura et al., 2016)發現，弧前應力在2011年Mw9日本地震前總體呈擠壓狀態，但是地震后呈拉張狀態而產生正斷層地震.這些應力變化的總體趨勢和圖6的結果一致.需要指出的是，本文中的解析解假設理想彈塑性楔形體、均一的楔形體介質和底部摩擦邊界，而實際增生楔具有高度不均一性.因此實際應力狀態比本文中的結果復雜.基于本文介紹的動態庫侖楔形體理論，Wang等(2019)認為斷層面摩擦系數需要很小(～0.032)才能產生弧前這種應力狀態的地震前后改變.

Ranero 和 Sallarès(2004)基于層析成像數據認為納斯卡板塊在北部智利俯沖時，其上地幔頂部約20 km厚的巖石圈可能含有～17%的蛇紋石，表明可能含有2.5wt%的水.這些含水礦物伴隨著俯沖溫壓條件的改變而產生脫水(Moore and Vrolijk, 1992; Hyndman and Davis, 1992; Davis et al., 2006).脫水反應導致流體可能沿俯沖通道(von Huene et al., 2004)或者沿上覆板塊斷裂系(Ranero et al., 2008)運移到淺部.更多的弧前洋底流體觀測數據有助于我們了解孔隙水壓比在地震周期的變化規律，利用動態庫侖楔形體理論從而可以更好的理解俯沖帶孕震機制和動力學過程.

4 結論

基于理想彈塑性楔形體材料的應力函數解析解(23)式以簡潔的形式描述了楔形體在重力和底部靜態摩擦共同作用下的內部應力狀態.該解析解不僅能描述楔形體處于穩定狀態的應力分布，而且能夠描述楔形體處于臨界破裂狀態的應力.經典臨界楔形體理論應力解析解從而成為(23)式的子集.

基于應力函數解(23)式提出的動態庫侖楔形體理論認為弧前幾何形狀和構造形變特征的差異性可能反映了俯沖斷層面上摩擦性質的不同.弧前海溝附近地表坡度比較陡，地震反射剖面顯示復雜的永久變形(外部楔形體).而更遠離海溝部分則地表坡度比較平緩，地震波反射體呈水平分布，通常存在未受強烈構造活動擾動的沉積盆地(內部楔形體).動態庫侖楔形體理論認為內部楔形體底部為生震帶，楔形體在地震周期主要產生彈性形變.而外部楔形體底部摩擦性質為速度強化，地震的時候斷層面摩擦系數增加，同時地震的擠壓導致外部楔形體孔隙流體壓力比升高.更強的斷層面摩擦性質和更弱的楔形體材料共同作用導致外部楔形體可能達到擠壓型破裂并且產生永久變形.地震以后內部和外部楔形體均逐漸恢復到震前穩定狀態.

致謝謹以此文紀念北京大學地質學系王仁教授誕辰100周年.本文主要內容來自于作者在加拿大維多利亞大學博士學習期間發表的研究成果，相關工作和作者博士導師王克林教授(Kelin WANG)合作完成.感謝徐世慶老師、韓鵬老師和另外兩位匿名審稿人提出的有益建議幫助完善本論文.