基于深度卷積神經網絡的2021年5月21—22日云南漾濞地震和青海瑪多地震震級估算

朱景寶，宋晉東，李山有*

1 中國地震局工程力學研究所 地震工程與工程振動重點實驗室，哈爾濱 150080 2 地震災害防治應急管理部重點實驗室，哈爾濱 150080

0 引言

地震預警是減輕地震造成人員傷亡和財產損失的有效手段之一.地震預警依據P波傳播速度比S波傳播速度快的原理，利用臺站記錄到的P波初期信息對地震基本參數和破壞區域進行估算，搶在破壞性地震波到達之前向公眾發布預警信息，進而讓人們提前幾秒或數十秒采取緊急避險措施(馬強，2008; 宋晉東，2013).世界上一些地震較為活躍的國家和地區已經建立了地震預警系統，如：美國(Allen et al., 2009; Kuyuk et al., 2014)、日本(Hoshiba et al., 2008; Kamigaichi et al., 2009)、意大利(Satriano et al., 2011; Colombelli et al., 2020)、中國臺灣(Wu and Teng, 2002; Hsiao et al., 2009)、墨西哥(Aranda et al., 1995; Suárez et al., 2018)等.同時，中國地震預警系統也在進行驗證測試(Peng et al., 2011; Zhang et al., 2016).

在地震預警系統中，地震破壞區域的準確估算以及可靠的預警信息發布依賴于震級估算的結果，因此準確而快速地估算震級，是地震預警系統的重要工作之一，對地震預警也有重要的意義.傳統震級估算方法主要根據P波觸發后單一特征參數與震級的經驗關系，進而估算震級(張紅才等, 2012).常用的特征參數包括幅值類參數(Wu and Kanamori, 2005; Wu and Zhao, 2006)、周期類參數(Kanamori, 2005; B?se, 2006; Huang et al., 2015)和能量類參數(Reed and Kassawara, 1990; Nakamura, 2003; Festa et al., 2008).盡管上述特征參數已經被證明與震級存在一定的線性關系，但是某一特征參數包含與震級相關的信息較單一，導致震級估算結果的誤差較大，并且震級估算結果也存在一定程度的小震高估和大震低估問題.因此，一些研究人員嘗試采用雙參數對震級進行估算，相對于單參數震級估算結果，有效提高了震級估算的準確性(Cuéllar et al.，2018).

近年來，人工智能已被引入到地震預警震級估算研究中.一些學者也嘗試將多個地震預警參數與機器學習方法相結合，進而對最終震級進行估算(Münchmeyer et al.，2020；朱景寶等，2021a).Zhu等(2021)使用日本K-net臺網數據，融合多種類型的12個P波初期特征參數(幅值類參數、周期類參數、能量類參數、衍生類參數)作為卷積神經網絡的輸入，構建了P波到達后3 s時間窗下的DCNN-M模型，進而用于地震預警震級估算，其結果優于傳統的單參數τc方法和Pd方法.Ochoa等(2018)基于支持向量機回歸算法，在單臺情況下，使用P波觸發后5 s的信號得到的25個參數(與方位角相關的參數、與震級相關的參數、與震中距相關的參數)作為輸入，進而對里氏震級進行估算，其結果表明：對于ML4.5以下的地震，震級估算有較小誤差，且平均絕對誤差為0.19個震級單位.此外，還有一些學者嘗試將地震波形數據與機器學習方法相結合，進而改進震級估算結果.胡安冬和張海明(2020)使用日本Kik-net和K-net臺網強震動數據建立了NN網絡用于地震預警震級估算，將波形的頻譜信息作為模型輸入，并發現在3 s時間窗內，該方法優于傳統的單參數τc方法，同時也認為多特征組合輸入的使用將會得到更優異的震級估算模型.Mousavi和Beroza(2020)基于30 s的波形輸入，構建了一個由卷積神經網絡和循環神經網絡組成的震級估算模型，有效改善了震級估算結果.然而，已經建立的人工智能地震預警震級估算模型對于中國地震的震級估算是否可行亟待研究.

2021年5月21日和22日，在中國云南漾濞和青海瑪多分別發生了MS6.4地震和MS7.4地震，同時還伴隨一些前震和余震的發生.據大理市抗震救災指揮部和青海省應急管理廳發布的消息，地震造成一定程度的人員受傷，以及交通、通信、供水等基礎設施的破壞.這次地震得到了國內許多研究者的關注，也為人工智能地震預警震級估算模型測試驗證提供了數據支持.

本文依據Zhu等(2021)提出的P波到達后3 s時間窗的DCNN-M模型框架，分別使用P波到達后1～40 s不同時間窗的特征參數作為輸入進行訓練和驗證，構建不同時間窗下的單臺DCNN-M模型，并采用多臺加權平均方法對2021年5月21日和22日發生在中國云南漾濞和青海瑪多的主震、余震和前震進行實時震級估算分析，旨在探索DCNN-M模型對這次漾濞地震和瑪多地震震級估算的可行性、以及未來在我國人工智能地震預警系統應用的可能性.

1 方法

卷積神經網絡主要用于信號數據的處理以及提取數據層次特征.Zhu等(2021)使用日本K-net臺網強震動數據并基于深度卷積神經網絡構建了P波到達后3 s時間窗下的單臺DCNN-M模型，其目的是為了提高地震預警震級估算的準確性；同時，Zhu等(2021)研究結果表明：對于MJMA3～7.5的地震事件，在P波到達后3 s時間窗下，DCNN-M模型的震級估算結果的準確性高于傳統的單參數τc方法和Pd方法，且沒有出現明顯的小震高估和大震低估現象.

1.1 特征參數

由于深度學習的特征提取是黑箱子，提取特征的物理意義并不明確.因此，DCNN-M模型的輸入不同于Mousavi和Beroza(2020)、胡安冬和張海明(2020)等采用的波形輸入，而是采用與震級相關的特征參數組合作為輸入，再通過DCNN-M模型提取這些特征參數的高階特征，使得該模型具有物理意義(Zhu et al., 2021).該模型的輸入是由4類特征參數，共12個特征參數組成的一維向量，幅值類參數包括峰值位移Pd(Wu and Zhao, 2006)、峰值速度Pv和峰值加速度Pa(Wu and Kanamori, 2005)；周期類參數包括特征周期τc(Kanamori, 2005)、峰值比Tva(B?se, 2006)、構造參數(Huang et al., 2015)；能量類參數包括速度平方積分IV2(Festa et al., 2008)、累積絕對速度CAV(Reed and Kassawara, 1990)、累積能量變化率DI(Nakamura, 2003)；衍生類參數(Zhu et al., 2021)包括豎向累積絕對位移cvad、豎向累積絕對速度cvav、豎向累積絕對加速度cvaa.

1.2 DCNN-M模型

DCNN-M模型的網絡結構是由四個卷積層、四個Batch Normalization層(BN層)、四個池化層和三個全連接層組成(Zhu et al.，2021).四個卷積層中卷積核的數目分別是124、150、190和250；卷積核的大小為4，移動步長為2，padding類型使用的是“same”；池化層采用的是最大池化，每個池化核的大小是2，移動步長是2；三個全連接層神經元數量分別是250、125、60；最后一個輸出層的神經元數目是1，輸出結果為預測震級.

本文在Zhu等(2021)提出的P波到達后3 s時間窗下的DCNN-M模型框架以及超參數的基礎上，同樣采用Zhu等(2021)所使用的訓練數據集和測試數據集的日本K-net強震數據，分別計算了P波到達后1～40 s不同時間窗的特征參數作為輸入，并對模型進行訓練和驗證，進而構建了在P波到達后不同時間窗下的單臺DCNN-M模型.

由于30 s之后的震級估算結果趨于穩定狀態，所以圖1展示了P波到達后1～30 s不同時間窗下的單臺DCNN-M模型對驗證數據集(這里的驗證數據集是指Zhu等(2021)文獻中所使用的測試數據集)的震級估算結果.圖中紅色實線是編目震級與估算震級的1∶1線性關系；紅色虛線表示±0.5震級單位誤差范圍；σ是估算震級與編目震級誤差的標準差，用于衡量誤差的離散性.從圖1中可以發現：隨著P波到達后時間窗的增加，震級估算誤差逐漸減小，且對于6級以上震級低估問題也逐漸改善.

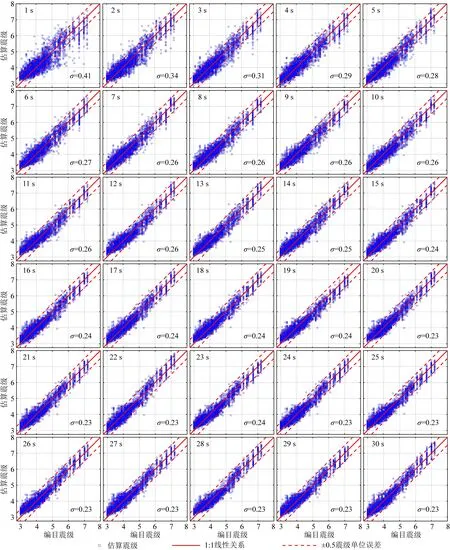
圖1 驗證集在1～30 s時間窗下震級估算結果Fig.1 Magnitude estimation at 1～30 second time window for validation dataset

1.3 多臺加權平均

圖2展示了構建的單臺DCNN-M模型對訓練集和驗證集震級估算誤差的標準差與P波到達后時間窗的關系.從圖2中可以發現：訓練集和驗證集的震級估算誤差標準差比較接近，且隨著時間窗的增加逐漸減小，這也說明我們所構建的P波到達后1～40 s的不同時間窗下DCNN-M模型有較好的連續性和泛化能力.

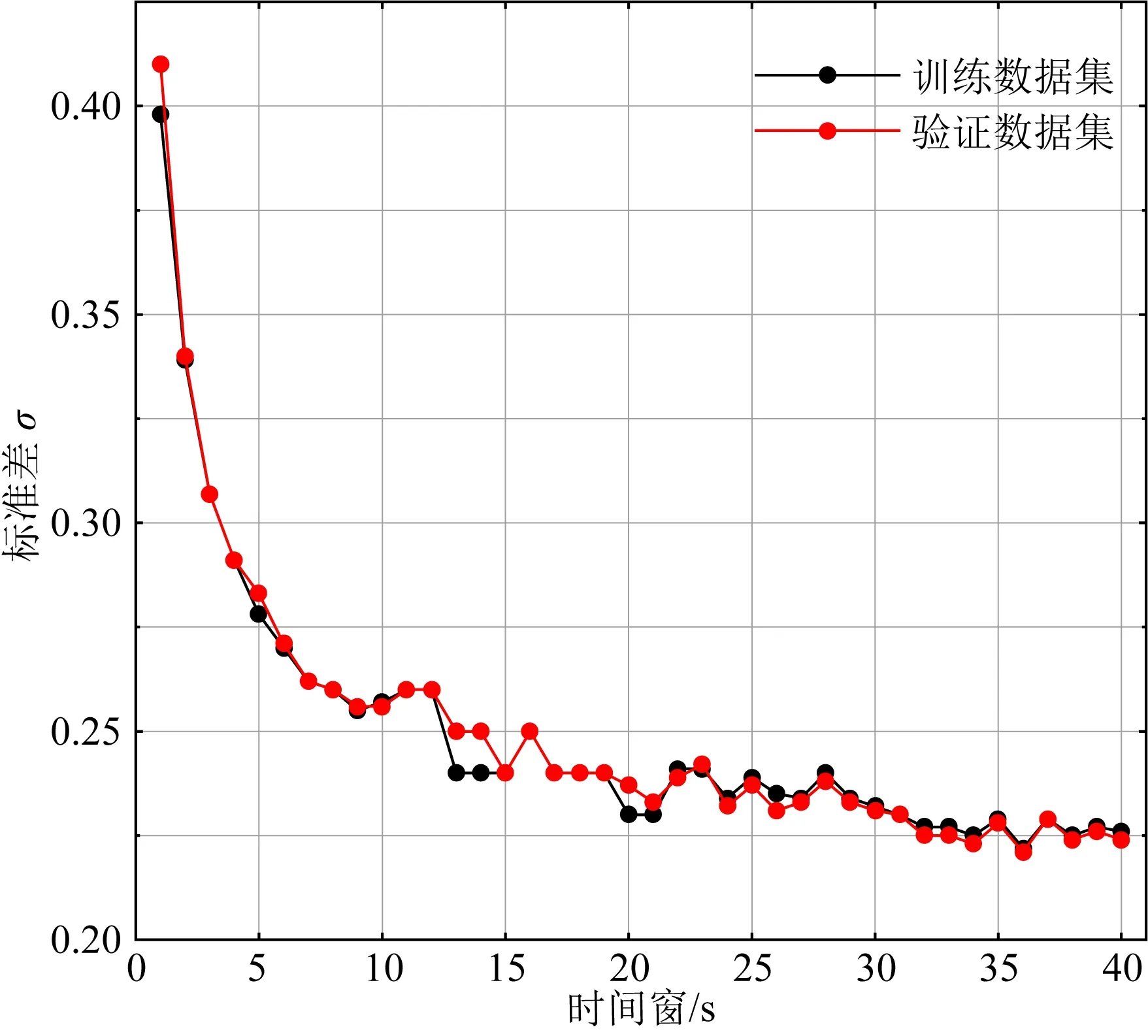
圖2 基于DCNN-M模型的訓練數據集和驗證數據集的震級估算誤差標準差與時間窗的關系Fig.2 Relationship between standard deviation of magnitude estimation error and time window for training dataset and validation dataset based on DCNN-M model

我們將基于P波到達后不同時間窗下建立的單臺DCNN-M模型以及多臺加權平均方法對2021年5月21日和22日發生在中國云南漾濞和青海瑪多的主震、余震和前震進行實時震級估算.

根據圖2中驗證集的震級估算誤差標準差隨著時間窗的增加而減小，且驗證集反映的是模型的性能，同時，標準差反映的是相應時間窗時模型在單臺情況下的震級估算的離散程度.因此，隨著時間窗的增加，震級估算的標準差越小，說明單臺的震級估算準確性越高，所以在多臺加權平均計算的時候，權重與驗證數據集在P波到達后相應時間窗下的DCNN-M模型震級估算的標準差成反比(Colombelli et al., 2012; Peng et al., 2017).

實時多臺震級加權平均計算公式如下：

(1)

(2)

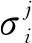
2 數據及處理

中國地震局工程力學研究所為本研究提供了2021年5月21—22日云南漾濞和青海瑪多地震的強震動數據，震級范圍MS4.0～7.4，共11次地震事件，129條三分向地震記錄.在本研究中，沒有對數據的震中距以及信噪比進行篩選.另外，DCNN-M模型是基于日本K-net臺網建立的，采用的震級標度是MJMA；這兩次地震序列的震級標度采用的是MS.依據Peng等(2017)、Kuyuk和Allen(2013)、Olson和Allen(2005)建立多國家多地區震級統計關系對于震級標注的處理方式，即不區分震級標度，本研究將估算震級標度統一記作為M.

圖3展示了本研究中震中以及臺站的分布，記錄到青海瑪多MS7.4主震的最近臺站是63DAW,震中距為175.6 km，且UD、EW、NS方向的最大加速度分別為-19.1 cm·s-2、46.0 cm·s-2、40.6 cm·s-2；記錄到云南漾濞MS6.4主震的最近臺站是53YBX,震中距為7.9 km，且UD、EW、NS方向的最大加速度分別為-448.4 cm·s-2，-379.9 cm·s-2，-720.3 cm·s-2(朱景寶等，2021b).

對于本研究中采用的地震記錄，首先采用馬強等(2013)提出的P波撿拾方法確定P波到時；然后對加速度記錄進行一次積分得到速度記錄，再對速度記錄進行一次積分得到位移記錄，并對積分后的結果使用4階0.075 Hz的巴特沃斯濾波器進行高通濾波，以消除積分帶來的低頻飄移的影響(Peng et al., 2017; 宋晉東等, 2018).

3 結果

為了驗證DCNN-M模型對于漾濞和瑪多地震震級估算的魯棒性，圖4和圖5分別展示了云南漾濞MS6.4主震和青海瑪多MS7.4主震在首臺觸發后實時的震級估算結果，以及觸發臺站數隨首臺觸發后時間增加的變化.圖4和圖5的橫坐標是首臺觸發時間，即第一個觸發的臺站后n秒.圖中黑色實線表示實際震級；黑色虛線表示實際震級±0.5震級單位誤差范圍；紅色實線表示首臺觸發后，n秒內DCNN-M模型對已觸發臺站震級估算結果的多臺加權平均值；藍色虛線表示距離震中最近臺站的震級估算結果；其他顏色的實線表示已經觸發的單個臺站的震級估算結果.

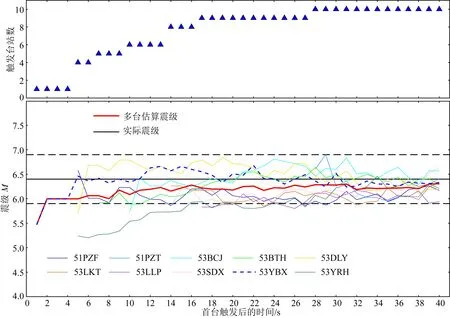
圖4 云南漾濞6.4級主震的震級估算結果Fig.4 The magnitude estimation of Yunnan Yangbi MS6.4 mainshock

從圖4中可以觀察到：對于漾濞主震，大部分臺站的單臺震級估算結果都分布在±0.5震級單位誤差范圍內，這表明本文訓練后的DCNN-M模型具備單臺震級估算準確性；首臺觸發后2 s時，DCNN-M模型的震級估算結果為M6.0；隨著首臺觸發時間的增加，估算震級逐漸接近實際震級，且在首臺觸發后9 s時，DCNN-M模型的震級估算結果為M6.2；同時，隨著首臺觸發時間的持續增加以及觸發臺站數的增加，DCNN-M模型的震級估算結果仍在不斷接近實際震級.

從圖5中可以觀察到：對于青海瑪多MS7.4主震，大部分臺站的單臺震級估算結果都分布在±0.5震級單位誤差范圍內，只有63DAW、63HEN、63XIH、63GUD臺站在觸發后1 s內震級估算結果在±0.5震級單位誤差范圍以外，這表明本文訓練后的DCNN-M模型具備單臺震級估算準確性；首臺觸發后1 s時，DCNN-M模型的震級估算結果為M6.4，可以判斷青海瑪多主震為一次大震；首臺觸發后2 s時，DCNN-M模型的估算震級是M7.0；隨著首臺觸發后時間的增加，在首臺觸發后9 s時，DCNN-M模型的估算震級是M7.3；且隨著首臺觸發后時間的持續增加和觸發臺站數的增加，DCNN-M模型的震級估算結果也逐漸接近實際震級.

圖6展示了這11次地震事件基于DCNN-M模型的震級估算誤差隨首臺觸發后時間的變化.圖中紅色實線表示青海瑪多MS7.4主震的震級估算誤差；藍色實線表示云南漾濞MS6.4主震的震級估算誤差；綠色實線表示漾濞余震以及前震的震級估算誤差；黑色虛線表示±0.5震級單位誤差范圍.從圖中可以看到：首臺觸發后1 s時，對于余震以及前震的震級估算誤差主要集中在±0.5震級單位范圍內，對于云南漾濞MS6.4主震和青海瑪多MS7.4主震的震級估算結果分別是M5.5和M6.4，誤差接近1.0震級單位，對于瑪多主震和漾濞主震在首臺觸發后1 s時低估的原因可能是大震在發生后幾秒內并沒有完全破裂，且P波并未攜帶完整的與震級相關的信息；但是在首臺觸發2 s以后，云南漾濞MS6.4主震和青海瑪多MS7.4主震的震級估算誤差都在±0.5震級單位內，且隨著首臺觸發后時間的增加，誤差逐漸減小，該結果也與圖4和圖5的結果相一致.

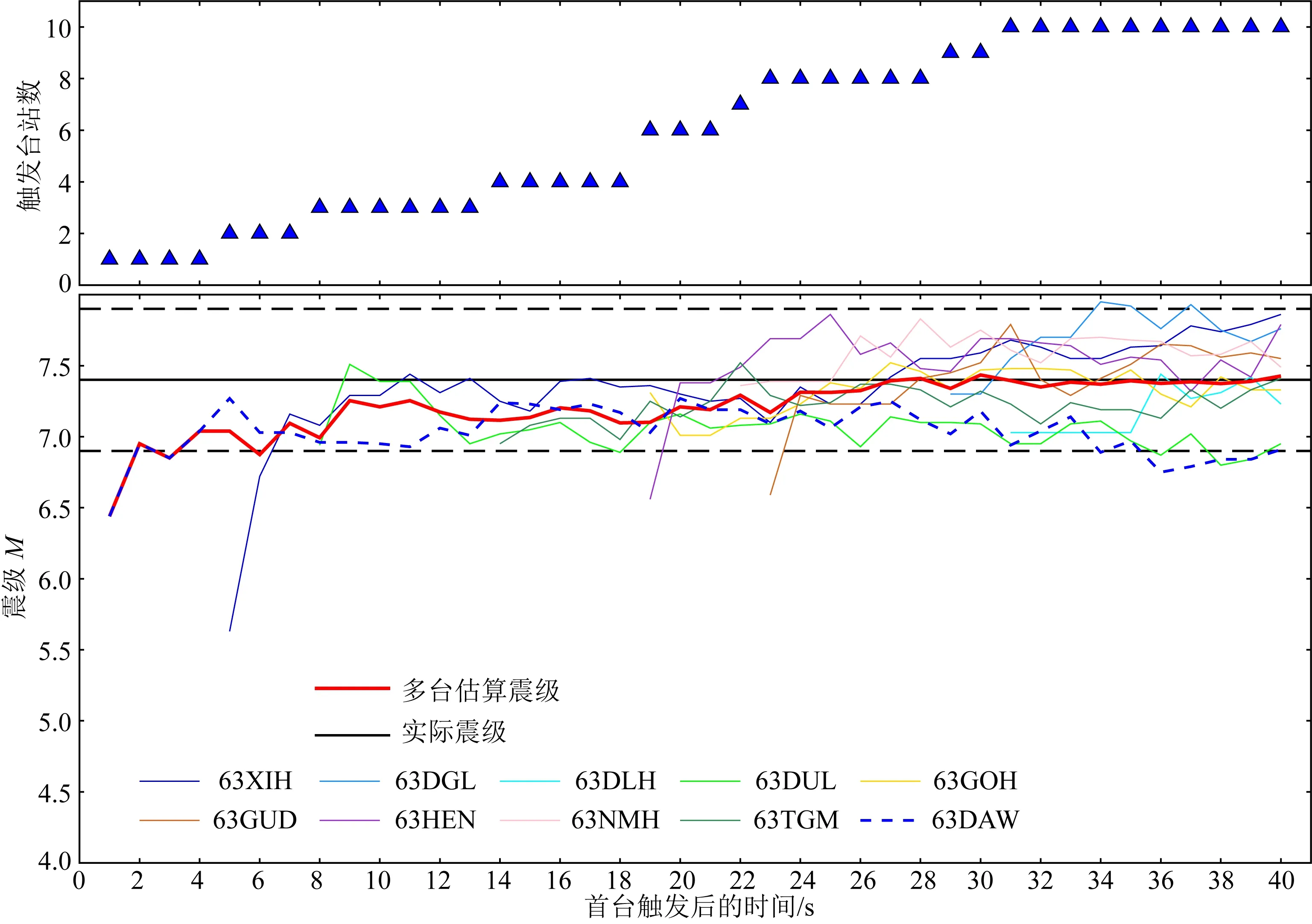
圖5 青海瑪多7.4級主震的震級估算結果Fig.5 The magnitude estimation of Qinghai Madoi MS7.4 mainshock

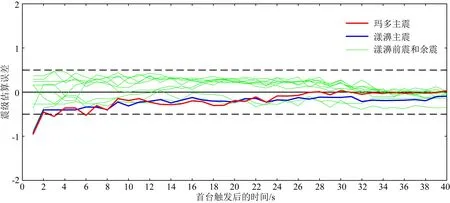
圖6 震級估算誤差隨首臺觸發后時間的變化Fig.6 The variation of magnitude estimation error with the trigger time of the first station

4 討論與結論

本研究在Zhu等(2021)使用日本的K-net強震動數據構建的P波到達后3 s時間窗的DCNN-M模型框架和超參數的基礎上，分別使用P波到達后1～40 s不同時間窗下的特征參數作為輸入進行訓練，構建了在P波到達后不同時間窗下的單臺DCNN-M模型，并對2021年5月21—22日云南漾濞和青海瑪多的MS4.0到MS7.4共11次地震進行震級估算，分析了基于單臺DCNN-M模型和多臺加權平均方法得到的震級估算結果隨首臺觸發后時間的變化，探索了DCNN-M模型對于這幾次地震在地震預警震級估算中的可行性.

通過對云南漾濞MS6.4主震和青海瑪多MS7.4主震在首臺觸發后實時的震級估算結果的觀察：在首臺觸發后2 s時，DCNN-M模型對云南漾濞地震的主震和青海瑪多地震的主震的震級估算結果分別是M6.0和M7.0；在首臺觸發后9 s時，DCNN-M模型對云南漾濞主震和青海瑪多主震的震級估算分別是M6.2和M7.3；隨著首臺觸發后時間的增加和觸發臺站數量的增加，震級估算結果逐漸接近實際震級.同時，這兩次地震事件的前震和余震，在首臺觸發后1 s時，震級估算的誤差主要都集中在±0.5震級單位內；隨著首臺觸發后時間的增加，這11次地震事件的震級估算誤差逐漸減小.本文的研究結果表明：DCNN-M模型對于2021年5月21—22日發生在中國云南漾濞和青海瑪多的11次地震事件在首臺觸發后10 s內可以得到較為穩定的震級估算結果.這為我國建立人工智能地震預警系統提供了潛在可能.但是，對于深度卷積神經網絡震級估算模型DCNN-M在中國地震預警系統中的應用還需要大量的中國數據進行驗證和測試.

需要注意的是，由于作為DCNN-M模型輸入的幅值類參數、能量類參數和衍生類參數是需要進行震源距修正，統一校正到參考震源距10 km(Zollo et al., 2006; 彭朝勇等, 2013)，其目的是為了消除幅值類參數、能量類參數和衍生類參數因距離衰減對震級估算的影響，所以在實際的地震預警過程中，DCNN-M模型準確的震級估算結果還依賴于地震預警系統的準確定位.此外，由于MJMA和MS這兩個震級標度并非完全相同，依據Peng等(2017)，只是近似的將這兩個震級標度相等，并且將估算震級統一記作M，而這兩種震級標度的差異性可能會對本研究的結果造成一定的誤差影響，對于這兩個震級標度的準確轉換仍需更深的研究和討論.

同時，本研究是基于日本K-net強震數據訓練得到的DCNN-M模型對漾濞和瑪多地震的主震、余震和前震進行震級估算.更進一步的改善對漾濞和瑪多地震的主震、余震和前震的震級估算結果，我們還考慮了兩種方案：一、在原有DCNN-M模型的基礎上加上中國強震數據進行遷移學習訓練，而是否可以成功應用遷移學習方法改進結果還存在爭議；二、使用中國目前已經公開的地震數據，建立屬于中國的DCNN-M模型，而對于目前中國的地震數據量是否可以建立泛化能力強且具有穩定性的模型還有待研究.這些方案也是我們對國內地震震級估算在下一步研究中需要探索的地方.

致謝中國地震局工程力學研究所為本研究提供數據支持.文中圖件使用通用制圖工具GMT(Genetic Mapping Tools)繪制.