軟時間窗多式聯運4PL路徑問題的改進烏鴉算法

唐懷洞，盧福強，王雷震，王素欣，畢華玲

1.東北大學 信息科學與工程學院，沈陽 110004

2.東北大學秦皇島分校，河北 秦皇島 066004

隨著我國經濟的飛速發展，物流行業也進入發展的快軌道。目前，第三方物流（the third party logistics，3PL）是物流界的主要商業模式，專門從事物流運輸服務。然而，隨著信息技術的不斷發展，3PL也出現了一些缺陷，3PL不能有效地利用各種資源，不能實現供應鏈的整體優化，單個3PL也難以完成跨區域、跨行業的物流業務。于是，第四方物流（the fourth party logistics，4PL）受到學者們和企業間的廣泛關注，4PL是集成管理咨詢和3PL服務的集成商，能夠根據客戶需求提供一套完整的運輸方案[1-2]。

4PL的特點決定了4PL路徑優化問題不同于傳統的車輛路徑問題，其需要在選擇物流路徑的同時選擇3PL服務商。一些學者在這一領域展開了相關的研究，但是這些研究大部分僅考慮的是3PL服務商的單一運輸方式，忽略了多式聯運能夠將不同運輸方式的優勢結合起來，提高運輸資源利用率，降低物流運輸成本的特點[3]。如黃敏等[4]建立考慮單一運輸方式的4PL路徑優化模型，并根據問題特點設計混合算法對模型進行求解；Huang等[5]根據不確定性理論建立單一運輸方式模糊規劃模型，并設計模糊仿真的兩步遺傳算法來尋找近似最優解。此外，在部分多式聯運路徑優化問題中，如賴志柱等[6]建立多軟時間窗約束的多目標路徑優化模型，并設計改進的粒子群算法進行求解，但其將部分中轉節點設為軟時間窗，貨物提前到達將產生存儲管理費用，延遲到達產生懲罰費用，而對于目前的多式聯運組織來講，完全可以做到在中轉節點進行各種運輸方式的無縫對接；楊文東等[7]利用蟻群算法求解了以總運輸成本最小為目標，目的節點為硬時間窗的雙層優化模型，然而在實際貨物運輸過程中，由于機械故障、天氣狀況等隨機因素的影響，可能會造成貨物不能在客戶要求的時間內到達，且運輸距離越長，中轉節點越多越容易發生，顯然，這種硬時間窗數學模型無法應對這種隨機情況。

由此可見，在以上研究的基礎上，研究目的節點帶有軟時間窗的多式聯運4PL路徑問題更具有實際意義和應用價值。目前解決4PL路徑優化問題的方法，主要以智能優化算法為主，比較典型的有遺傳算法[5，8]、和聲搜索算法[9]和蟻群算法[10]等，而烏鴉搜索算法是近年來新興的智能優化算法，且已經被證明在工程優化方面比遺傳算法、粒子群算法等效果更好[11]。于是，本文設計了基于天牛須搜索思想和萊維飛行機制的烏鴉搜索算法對問題進行求解，設計不同節點規模的算例驗證模型和算法的有效性。首先通過田口方法得出算法最優參數組合，并與其他算法進行結果比較分析，最后分別研究4PL集成商采用多式聯運運輸方式具有的優勢和軟時間窗不同時對實驗結果的影響。

1 數學模型

1.1 問題描述

某4PL公司承接了一項運輸任務，需要將一批貨物從起始節點運送到目的節點，運輸網絡多重圖如圖1和圖2所示。圖2中，數字1、2代表3PL服務商的標號，（1）、（2）、（3）代表3PL服務商的運輸方式。每段路徑上可能存在多個可以提供運輸服務的3PL服務商，每個3PL服務商可以提供多種運輸方式。在運輸貨物時會產生運輸費用和運輸時間，在中轉節點發生3PL服務商運輸方式的轉換時，會產生中轉費用和中轉時間。在目的節點設置為客戶要求的貨物到達時間窗，若貨物提前到達，則產生一定的存儲管理費用；若延遲到達，則產生一定的懲罰費用。綜合上述因素，4PL公司需要確定最佳的運輸路徑、3PL服務商及其運輸方式，使總運輸成本最低。

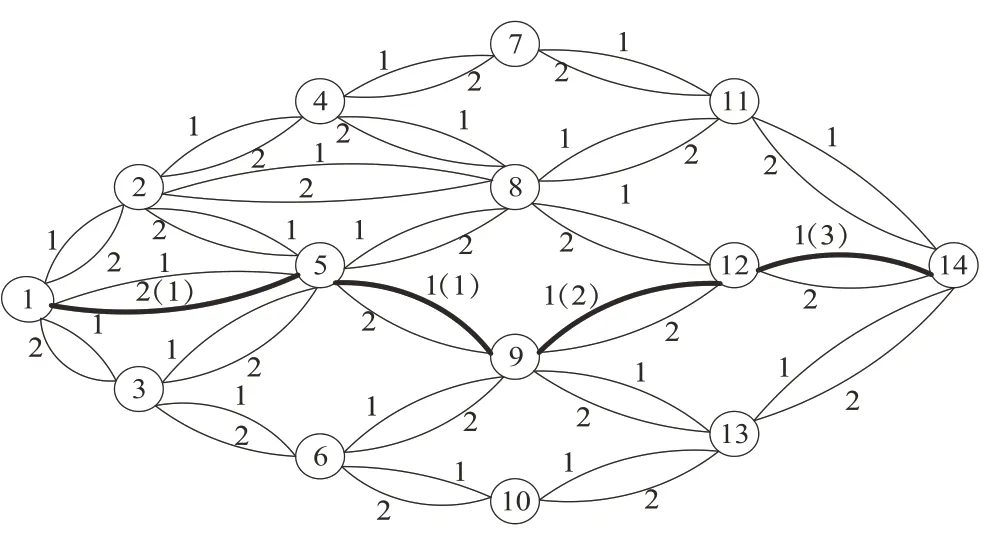
圖1 4PL運輸網絡多重圖Fig.1 4PL transport network multiple diagram

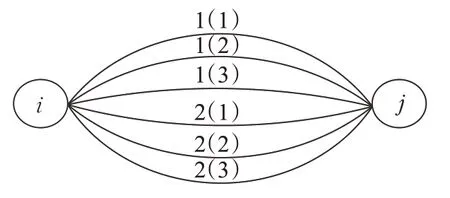
圖2 節點間運輸網絡圖Fig.2 Transport network diagram between nodes

1.2 模型構建

1.2.1 模型假設

（1）貨物在運輸路段上不可以更換運輸方式，一旦采取某個3PL服務商的運輸方式，那么必須到下一個節點才能換成另一種運輸方式。

（2）在任何一個中間節點，每個3PL服務商都有滿足換裝需求的各種運輸設備，即在任何中間節點處都可以發生各種運輸方式之間的轉換。

（3）在中間節點發生運輸方式轉換時，則只需考慮中轉費用和中轉時間，不需要考慮其他因素。

1.2.2 模型參數及變量描述

模型參數描述如下：

I為點集合，表示貨物運輸所經過的節點，i∈I,j∈I；

J為運輸方式的集合，表示運輸方式的種類，k∈J,z∈J；

r ij為相鄰兩節點間3PL服務商的數量，i∈I,j∈I；

Q為客戶需求量；

C kz j表示在節點j從運輸方式k轉換成運輸方式z需要的單位中轉費用；

P E為貨物提前到達目的節點，單位時間內需要支付的存儲管理費用；

Tmin為客戶要求貨物從起始節點至達到目的節點的最早時間；S D為貨物到達目的節點的時間；

P L為貨物延遲到達目的節點，單位時間內需要支付的懲罰費用；

Tmax為客戶要求貨物從起始節點至達到目的節點的最晚時間；

n為目的節點，n∈I；

決策變量描述如下：

xk ijl表示如果從節點i到節點j采用了第l(l=1,2,…,rij)個3PL服務商的第k種運輸方式，那么該值為1，否則為0；

y kz j表示如果在節點j從運輸方式k轉換成運輸方式z，那么該值為1，否則為0。

1.2.3 模型建立

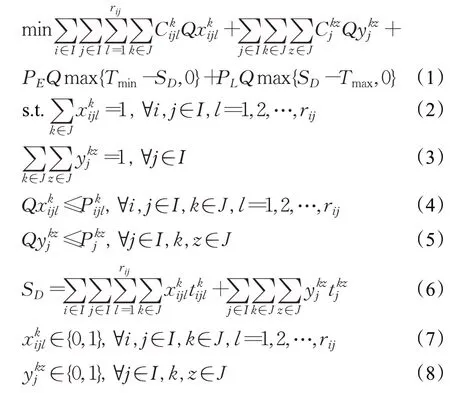
其中，式（1）是該模型的目標函數，表示最小化總運輸成

2 算法設計

考慮多式聯運的4PL路徑優化問題是NP-hard問題，目前的解決方法主要以智能優化算法為主，而烏鴉搜索算法[11]（crow search algorithm，CSA）是2016年提出的一種新興群體智能優化算法，與其他智能優化算法相比，該算法具有結構簡單、參數少、易于學習和掌握等優點，且已經成功應用于多個領域。但是，該算法的兩個位置更新策略均存在一定的盲目性，CSA存在求解精度低、收斂速度慢的缺陷。針對這一情況，本文引入代際信息交流機制和天牛須搜索思想對追隨領導者產生的位置更新策略進行改進，代際信息交流機制是使烏鴉個體追隨上代最優烏鴉個體位置進行移動，彌補了烏鴉個體位置更新盲目性的缺陷，天牛須搜索思想是比較天牛左右兩個觸角探測到的氣味強度來決定下一次的移動方向，提高CSA的尋優能力。針對CSA隨機產生位置的更新策略，引入了萊維飛行機制，它的特點是長時間的短距離移動，偶爾長距離移動，可以保證移動不會只停留在某個局部范圍，提高算法跳出局部最優的能力。

2.1 編碼和種群初始化

根據問題特點，采用雙列變長編碼機制[12]對烏鴉個體分兩段進行編碼，第一段表示路徑經過的節點集，第二段表示3PL服務商及其運輸方式集。采用Dijkstra算法[13]初始化烏鴉種群，首先將4PL運輸網絡多重圖處理成簡單網絡圖，即相鄰節點間僅有一個3PL服務商的一種運輸方式，然后計算每條邊上的權值，計算方式如式（9）：

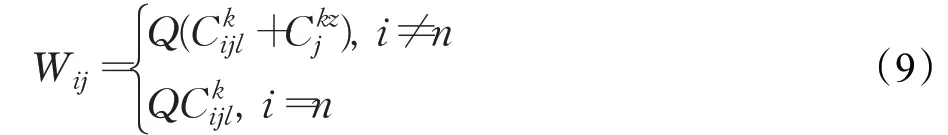
其中，Wij為相鄰兩節點之間邊上的權值，權值的計算為一條路徑上的貨物運輸費用與在節點產生的中轉費用之和。若是目的節點，則只需算一條路徑上的貨物運輸費用。

于是，運用Dijkstra算法通過簡單網絡圖求出一個初始解，重復此過程直至達到改進烏鴉搜索算法（levy beetle search algorithm，LBSA）設定的種群規模，從而產生問題的初始種群。

2.2 位置更新策略

利用LBSA的兩個位置更新策略進行解的更新，其中位置一更新策略，如式（10）第一個式子，烏鴉個體首先按照加入代際信息交流機制的CSA進行移動，然后將烏鴉個體視為天牛，進行天牛須算法（BAS）的移動。

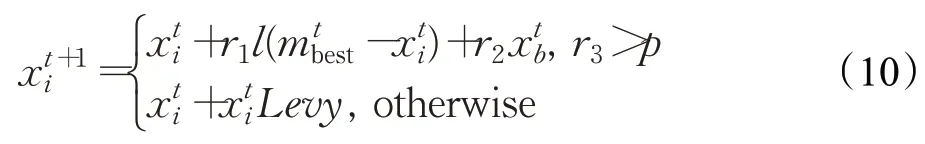
其中，x ti表示第t次迭代中第i個烏鴉的位置，xt+1i表示第t次迭代后第i個烏鴉的位置，r1、r2、r3均是服從[0，1]均勻分布的隨機數，l表示第t次迭代中第i個烏鴉的飛行距離，m tbest表示第t次迭代中烏鴉種群的最優位置，即引入的代際信息交流機制，使得烏鴉個體朝著上一代個體最優位置進行移動。xtb表示第t次迭代中按照BAS算法移動的距離，即位置增量，p為轉換概率，Levy為遵循Levy飛行的步長：

其中，μ、v服從標準正態分布，β=1.5。

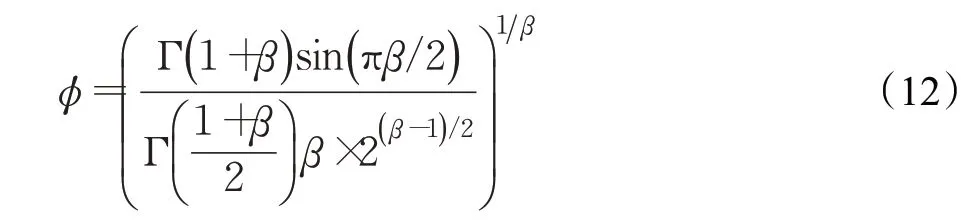
按照天牛須算法移動的位置增量xtb+1更新公式如式（13）：

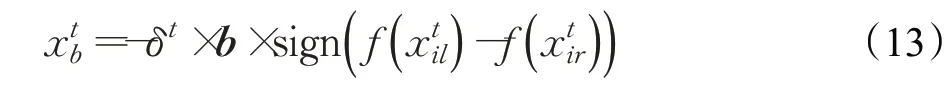
其中，δt表示第t次迭代中天牛的步長，δt=δt-1×eta，eta=0.95，表示步長的衰減系數。表示天牛右觸角指向左觸角的隨機單位向量，rands()為隨機函數，k為解的分量個數。sign為符號函數表示天牛左觸角位置的適應度值表示天牛右觸角位置的適應度值。

天牛左、右觸角位置更新公式為：

其中，d t=δt/c，表示兩觸角之間的距離，c=5。

2.3 適應度函數

將目標函數直接作為算法的適應度函數。若要求的是最小化目標函數，則只需要將解代入適應度函數中，求得的適應度值越小，則解越好，否則則越差。

2.4 算法步驟

LBSA算法步驟如下：

步驟1運用Dijkstra算法初始化烏鴉種群，并初始化種群規模NP，迭代次數NG，飛行距離l等參數。

步驟2根據適應度函數數計算初代個體的適應度值，選擇出當代最優解，初代個體的位置即為當前個體的最優解。

步驟3根據產生的均勻分布隨機數r3與轉換概率p的比較，利用式（10）進行解的更新。

步驟4根據適應度函數計算所有解的適應度值，通過比較，更新個體最優解和種群最優解。

步驟5重復步驟3和4直至到達最大迭代次數NG終止操作。

步驟6輸出最優解及其適應度值。

3 算例分析

為了驗證本文提出的數學模型和LBSA算法的有效性，設計了三種節點規模的算例，算例規模分別是7節點、14節點和28節點。首先通過田口方法獲得算法最優參數組合，然后與BAS、CSA、LCSA算法進行對比分析，驗證改進算法的有效性。其次將多式聯運與單一3PL服務商的單一運輸方式所產生的實驗結果進行對比分析，分析得出多式聯運能充分發揮不同運輸方式的優勢，有效降低總運輸費用，最后分析不同軟時間窗對實驗結果的影響。三種節點規模的算例使用的實驗數據均參考文獻[14]，并根據現實生活中三種運輸方式所具有的技術和經濟特點進行修改。本仿真實驗環境為：Windows10操作系統，主頻3.50 GHz，RAM8.00 GB，仿真軟件采用Matlab2015b。

3.1 算例描述

某4PL公司承擔了一項運輸任務，運輸貨物量為10，要求將貨物從起始節點送到目的節點，中間會經過多個城市節點。相鄰兩節點之間存在兩個3PL服務商，且每個3PL服務商可以分別提供三種運輸方式，即鐵路運輸、公路運輸和水路運輸（部分節點之間存在），每種運輸方式的運輸費用、運輸時間、運輸能力會有所不同。在目的節點加入一個軟時間窗，提前到達會產生一定的存儲管理費用，延遲到達會產生一定的懲罰費用。三種節點規模下的軟時間窗范圍分別為[35，40]、[50，55]、[81，86]，4PL集成商需要分別選擇出一套最小化總運輸費用的運送方案。由于篇幅原因，這里僅列出例1的相關數據。

表1中形如x/y/z的數據，其中x為單位費用，y為時間，z為運載能力；表2中數據的分子為單位中轉費用，分母為中轉時間。提前到達目的節點需要支付貨物存儲管理費用，單位時間費用為30，延遲到達目的節點需要支付懲罰費用，單位費用為40。

表1 例1運輸網絡多重圖中相鄰節點間數據Table 1 Example 1 data between adjacent nodes in transport network multiple graph

表2 運輸方式之間轉換情況Table 2 Switching between modes of transport

3.2 算法參數設置

采用田口方法[15]可以確定算法的最優參數組合。為了描述如何確定LBSA的最優參數組合，以14節點規模為例，介紹確定最優參數水平的過程。首先，確定算法的可控參數，分別是迭代次數NG、種群規模NP、飛行距離l、轉換概率p、天牛步長δ，然后測試5個參數的不同取值對實驗結果的影響，并經多次測試后選取算法性能表現較好的參數水平，如表3所示。

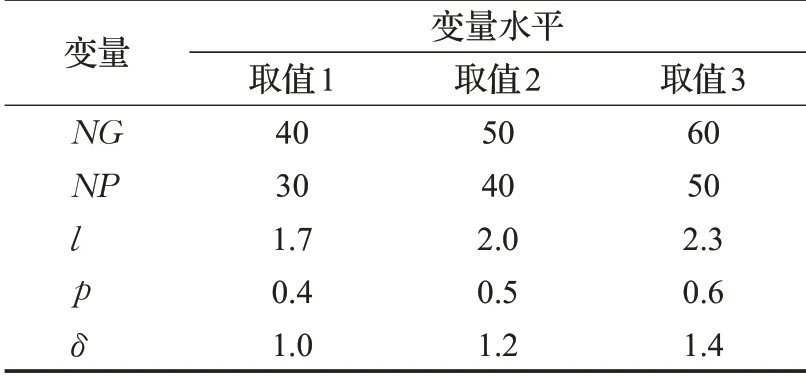
表3 LBSA算法參數及其水平Table 3 LBSA algorithm parameters and levels

按照正交表的創建方法，選取各參數水平的不同組合進行實驗研究，將每組參數組合代入到LBSA算法中運行50次，實驗結果的平均值放入正交表中，得到實驗結果如表4所示。

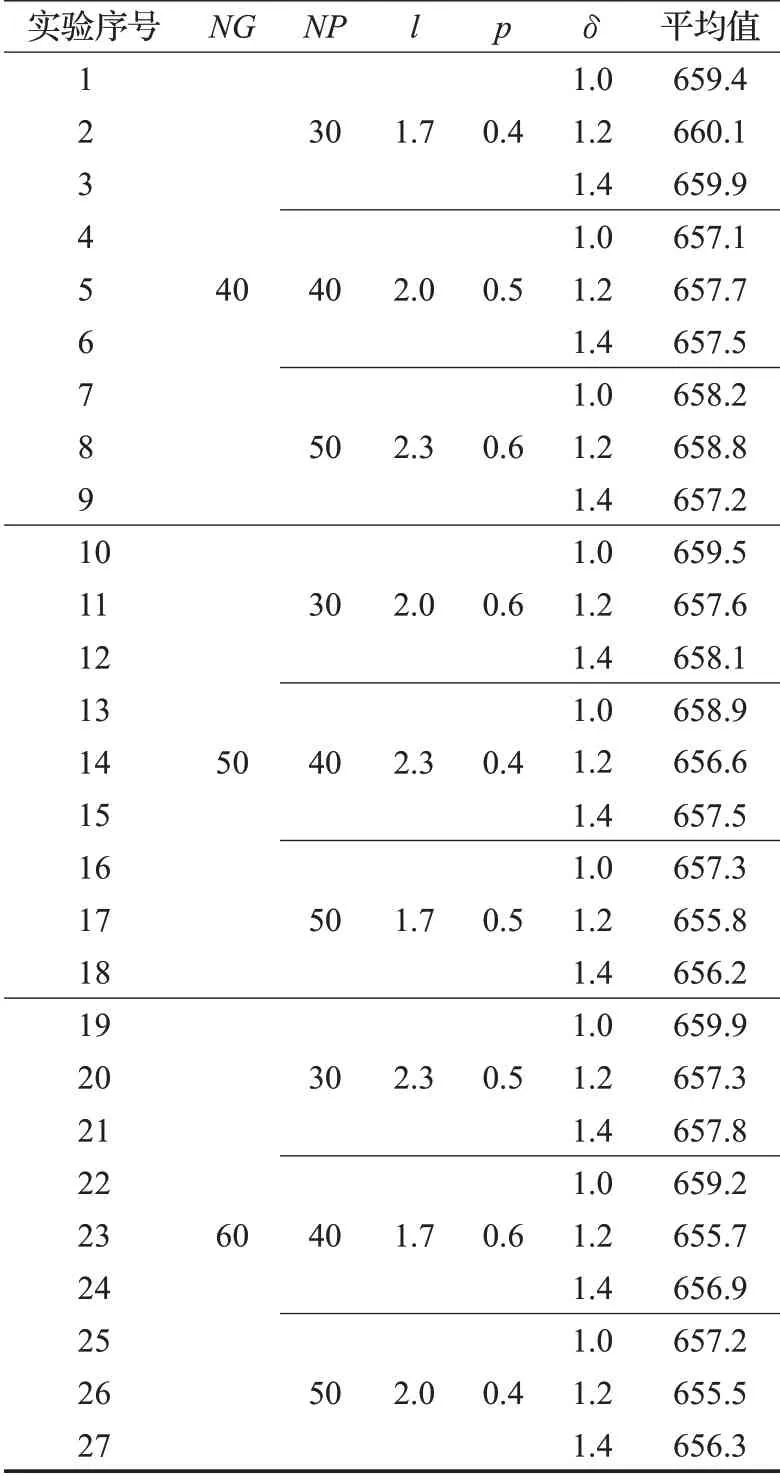
表4 正交實驗表Table 4 Orthogonal experiment table

然后運用Minitab17軟件分別得到參數的信噪比主效應圖和均值主效應圖，如圖3、圖4所示，從圖中可以看出，算法參數對信噪比的貢獻程度，信噪比的變化趨勢，以及參數對實驗結果的影響程度和變化趨勢。從圖3、圖4中可以看出，14節點規模算例下LBSA算法的最優參數組合分別為：NG=60、NP=50、l=2.0、p=0.5、δ=1.2。同樣，利用田口方法可以得到7節點和28節點的LBSA算法的最優參數組合，如表5所示。

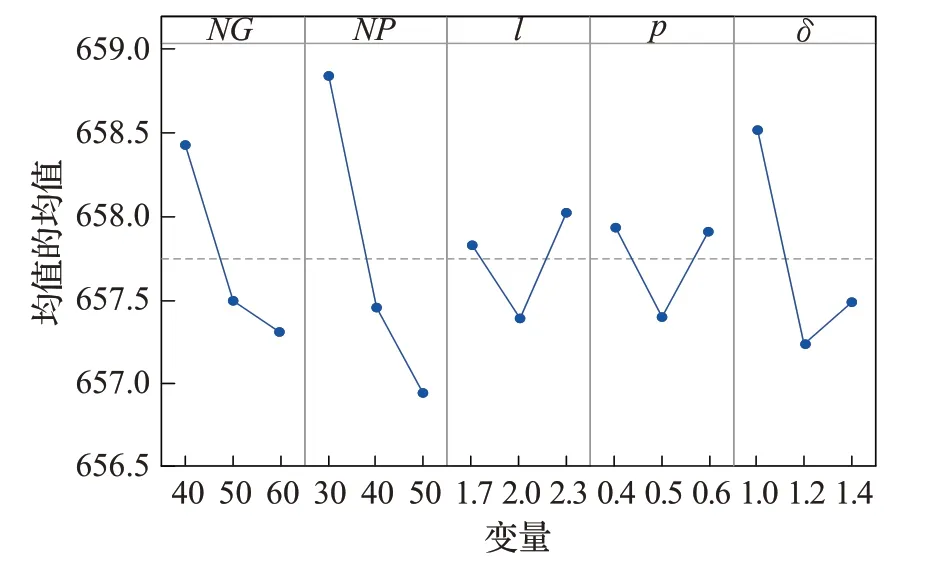
圖4 參數的均值主效應圖Fig.4 Main effect diagram for means of parameters

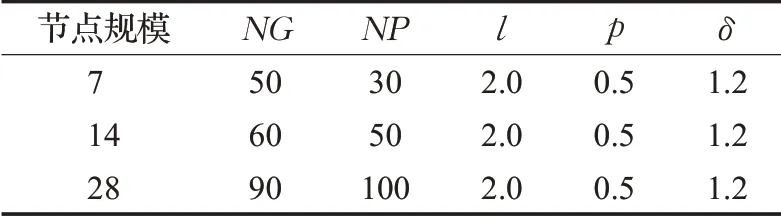
表5 不同節點規模的最優參數組合Table 5 Optimal parameter combination of different node sizes

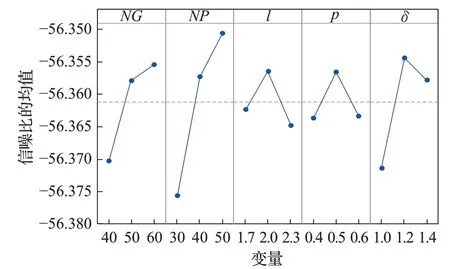
圖3 參數的信噪比主效應圖Fig.3 Main effect diagram for SNR of parameters

3.3 算法性能對比分析

針對三種不同規模的實驗案例，分別使用BAS、CSA、LCSA、LBSA算法進行運算，每種算法的參數組合都是經過上述田口方法求出，每種算法運行50次，得到的實驗結果如表6表示。由表6可知，在計算時間上，BAS算法運行最快，這是因為BAS算法只需要一個個體，而CSA、LCSA和LBSA算法運算時間相差不大。對于7節點規模案例，四種算法都可以求得最優值，但是CSA、LCSA和LBSA算法的最差值、平均值和標準差要優于BAS算法。對于14節點規模案例，BAS算法失效，無法求得最優值，并且CSA、LCSA和LBSA求得的最差值、平均值和標準差都要明顯由于BAS算法。對于28節點規模案例，BAS算法依舊失效，雖然CSA、LCSA算法求得了最優值，但最差值、平均值和標準差要較明顯差與LBSA算法。并且由表6可知，隨著節點規模的增大，LBSA算法的達優率和穩定性要遠高于BAS和CSA、LCSA算法。上述實驗結果證明LBSA算法在解決本文4PL路徑問題具有一定的有效性和優越性。

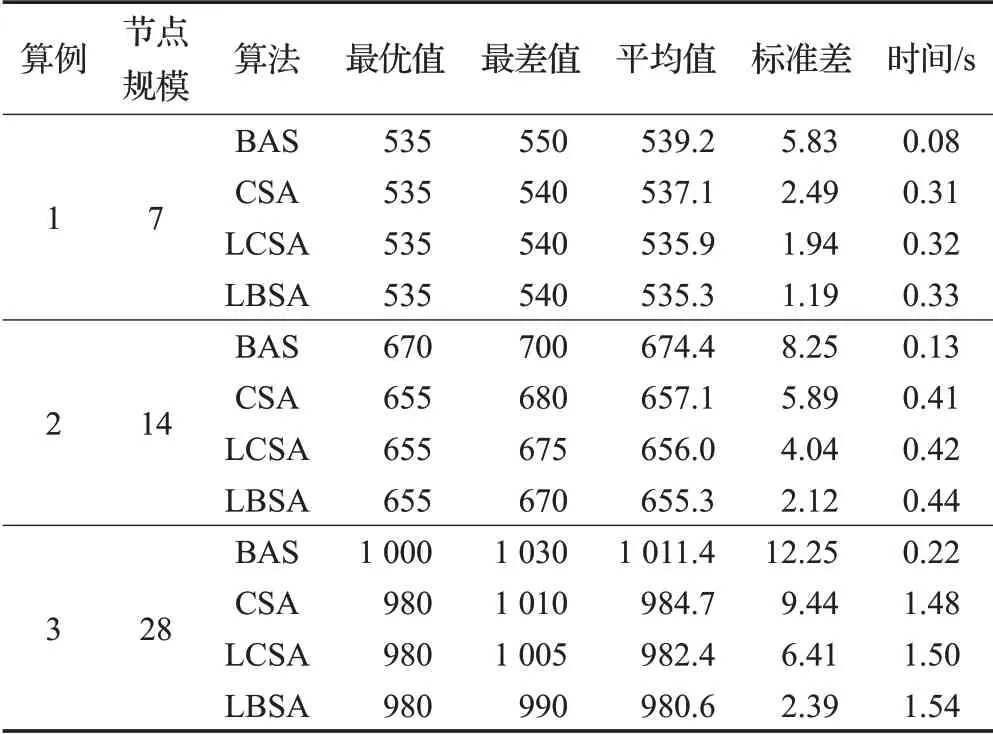
表6 算法實驗結果對比Table 6 Comparison of algorithm experimental results

3.4 實驗結果分析

運用LBSA算法求出三個算例下的最優運送方案，如表7所示。以算例2為例，介紹4PL公司為客戶選擇的運送方案。當客戶要求貨物到達目的地時間范圍為[50，55]時，貨物依次經過的城市節點為1、5、9、12、14，相鄰城市節點間依次選擇編號為2、1、1、1的3PL服務商，運輸方式依次為各3PL服務商的鐵路運輸、鐵路運輸、公路運輸和水路運輸，如圖1中加粗線所示。運用LBSA算法求得的三個算例結果收斂過程如圖5、圖6、圖7所示。

表7 不同節點規模下LBSA算法最優運送方案Table 7 LBSA algorithm optimal transportation scheme at different node sizes

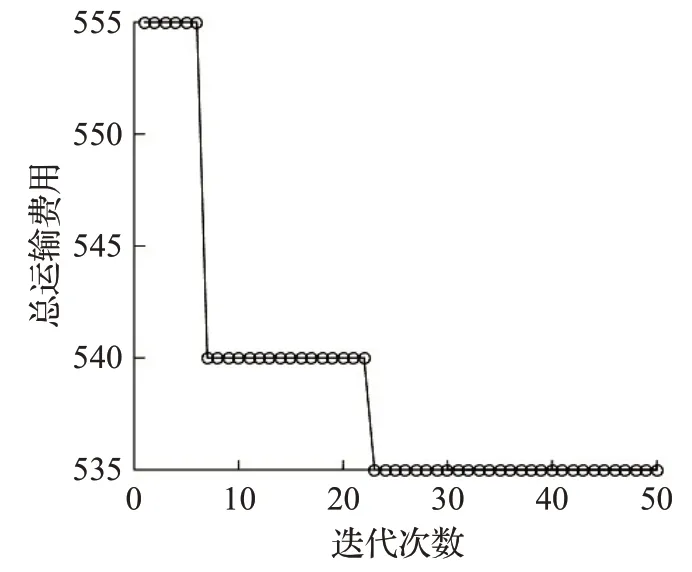
圖5 算法收斂過程（算例1）Fig.5 Algorithm convergence process（example 1）

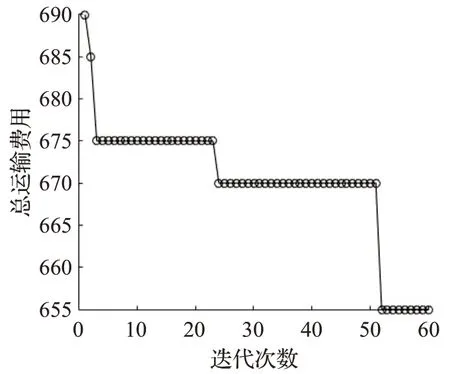
圖6 算法收斂過程（算例2）Fig.6 Algorithm convergence process（example 2）

圖7 算法收斂過程（算例3）Fig.7 Algorithm convergence process（example 3）

3.5 結果對比分析

為了更直觀地分析4PL公司通過不同3PL服務商采用多式聯運來降低總運輸費用的優勢，對表7中三種節點規模下的軟時間窗，分別畫出不同3PL服務商采用多式聯運與單一3PL服務商采用單一運輸方式所需總運輸費用的對比圖，如圖8、圖9和圖10所示。由于水路運輸只存在于部分城市節點，故不做分析，同時計算出各運輸方式所需的總運輸時間，如表8所示。

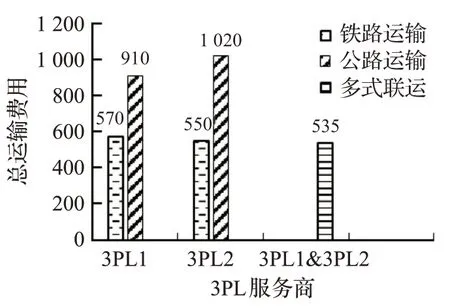
圖8 7節點運輸方式對比圖Fig.8 Comparison diagram of transportation mode of 7 nodes

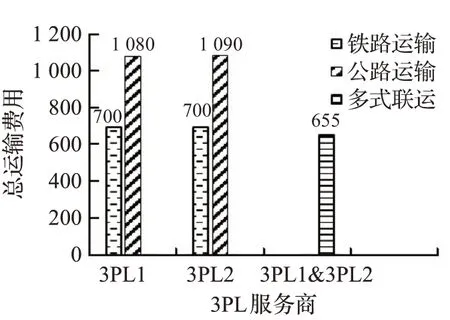
圖9 14節點運輸方式對比圖Fig.9 Comparison diagram of transportation mode of 14 nodes

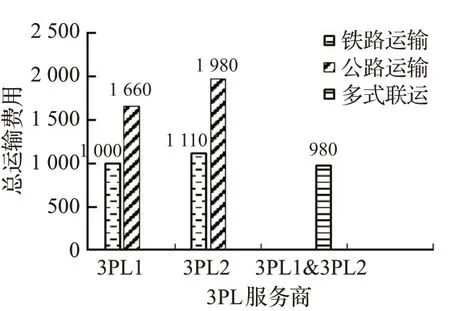
圖10 28節點運輸方式對比圖Fig.10 Comparison diagram of transportation mode of 28 nodes

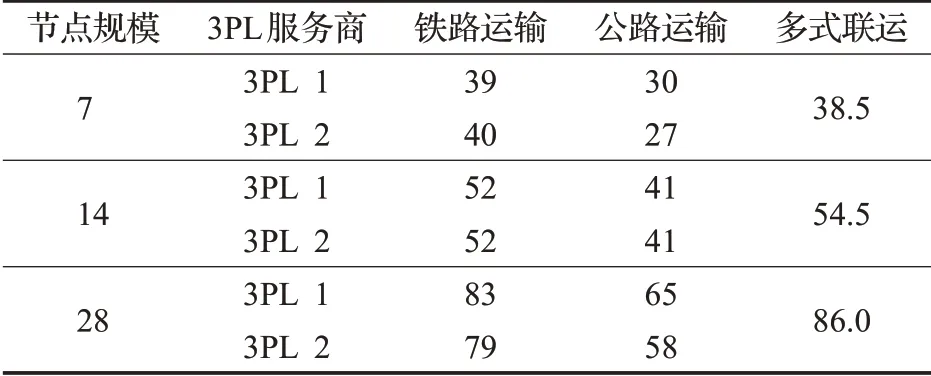
表8 各運輸方式所需運輸時間Table 8 Transportation time required by each mode of transportation

3.6 軟時間窗對實驗結果的影響

從圖8、圖9、圖10和表8中可以看出，雖然單一3PL服務商使用鐵路運輸和不同3PL服務商采用多式聯運運輸所需運輸時間相差不多，但運輸總運輸費用要比使用多式聯運運輸高。尤其是當單一3PL服務商使用公路運輸時，由于提前到達客戶要求時間過多，產生了大量的貨物存儲管理費用，導致總運輸費用偏高。從以上分析可以看出，4PL集成商采用多式聯運的運輸組織形式，能夠在滿足客戶要求的同時，有效地降低總運輸費用。因此，采用多式聯運能夠更好地為4PL集成商提供決策依據。

分析軟時間窗不同時對最優運送方案的影響。在分析軟時間窗對實驗結果的影響之前，先對無軟時間窗約束條件下的問題進行求解，即將數學模型中的存儲管理費用和懲罰費用公式去掉。求得28節點規模下的最小總運輸費用為900，花費時間99。以上述求得的時間為臨界點進行軟時間窗的劃分，來分析軟時間窗對實驗結果的影響，如表9所示。

從上述表中可以看出，隨著客戶對軟時間窗要求的范圍越來越小，4PL集成商會確定不同的最優運送方案，方案所需總運輸費用也越來越高。當客戶要求的軟時間窗范圍過小時，比如表9中軟時間窗范圍為[52，57]時，最優運送方案花費時間為58，同時58也是運輸網絡圖中所有運送方案花費時間最小者，如果研究的問題是硬時間窗，建立硬時間窗的數學模型，那么顯然無法解決這種情況，研究軟時間窗的路徑問題則更具有實際意義。在這些最優運送方案中，由于客戶要求的軟時間窗不同，盡管4PL集成商可能會選擇相同的運輸路徑，但3PL服務商及運輸方式的選擇會有所不同。這是因為4PL集成商能夠針對客戶不同的軟時間窗要求，及時做出決策，得到最優的運輸路徑、3PL服務商及其運輸方式的組合。

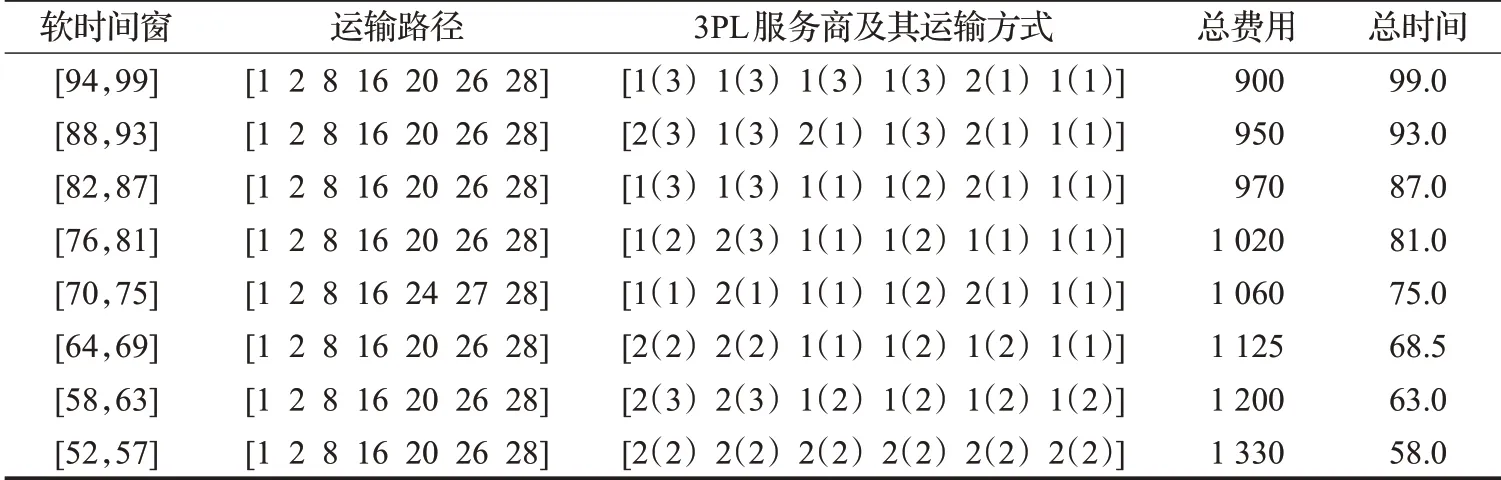
表9 例3軟時間窗對結果的影響Table 9 Example 3 effect of soft time window on result

4 結語

（1）考慮機械故障、天氣狀況等隨機因素在運輸過程中對各種運輸方式的影響，多式聯運能夠發揮各種運輸方式的優勢，建立軟時間窗的多式聯運4PL路徑優化模型。

（2）設計引入天牛須搜索思想和萊維飛行機制的烏鴉搜索算法對其進行求解。通過三種不同規模的算例驗證了LBSA在解決此問題時的有效性，擴展了此算法的應用領域。

（3）通過實驗結果對比分析得出，在滿足客戶的需求下，4PL集成商采用多式聯運的運輸方式相比單一3PL服務商采用單一運輸方式可以有效降低總運輸費用。接著以例3為例，分析了客戶要求的軟時間窗不同時，4PL集成商會確定不同的最優運送方案。

（4）本文還有一些不足之處，比如未考慮貨物量過多，超過任何一個3PL的任一運輸方式運載量的情況，在以后的研究中可以從這一角度出發。