諧振接地系統的配電線路接地故障選線新方法
田晶京,耿 芳,趙 峰,高鋒陽,李安樂
(蘭州交通大學 自動化與電氣工程學院,蘭州 730070)
諧振接地系統經消弧線圈接地方式具有易熄滅電弧和減小過電壓危害等優勢,廣泛應用于3~60 kV的中壓配電網中,由于消弧線圈的補償作用,導致故障電流微弱,零序電流方向不定[1]和出現“虛幻接地”[2]或“換相”[3]的現象,未徹底解決諧振接地系統故障選線問題,制約了配電網安全可靠供電運行。目前,主要利用故障信號暫態量實現故障選線[4-7],以零序電流的能量、電壓或電流幅值,極性和突變量為依據篩選故障線路。文獻[8]以“能量最大”為標準確定零序電流的特征頻帶,提出相對能量法實現故障選線;文獻[9]通過比較相鄰監測點故障電流的極性判別故障線路;文獻[10]根據故障時相電壓和相電流突變量之間的關系,提出一種故障定位方法。上述方法受到故障電流微弱、方向不定或換相影響出現選線失誤,因此,僅利用故障電流某一方面的特征構造選線依據具有片面性,當故障特征不明顯時,易出現誤判。配電線路發生單相接地故障時,故障線路與非故障線路間零序電流波形明顯區別于非故障線路間零序電流波形,從零序電流波形相似度出發,可將圖像相似度識別方法[11-14]應用在單相接地故障選線中。為此,提出一種接地故障選線新方法,該方法以線路間零序電流波形的相似程度為選線依據,對零序電流應用希爾伯特黃變換(HHT, Hilbert Huang transform)得到Hilbert時頻譜,再用時頻譜帶通濾波法重構各頻帶的零序電流,計算得到各線路故障電流的時頻能量矩陣,求得綜合相似系數矩陣完成故障選線。
1 時頻能量矩陣
1.1 HHT算法
HHT的處理對象是具有非平穩、非線性特性的零序電流信號,其步驟中的EMD(empirical mode decomposition)在分解故障信號時,獲得IMF分量隨著原始信號而變化,出現模態混疊問題[15]。因此,采用時頻譜帶通濾波法處理零序電流信號來解決上述問題,具體處理步驟見文獻[16]。
1.2 零序電流波形特征
在不同故障角下,饋線與母線故障時線路的零序電流波形,如圖1和圖2所示。
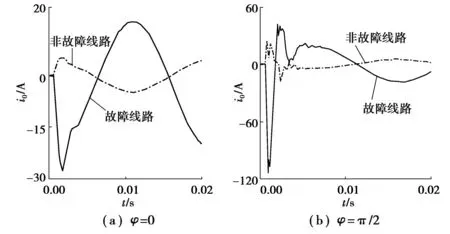
圖1 不同故障角下線路的零序電流波形Fig. 1 Zero-sequence current waveform of the circuit at different fault angles

圖2 母線接地時線路的零序電流波形Fig. 2 Zero-sequence current waveform of the circuit on bus-bar earthed fault
在φ=0時,零序電流主要是低頻感性電流;在φ=π/2時,零序電流主要是高頻電容分量,其余時刻,零序電流由2個不同頻率的電流合成[8]。由圖可知,饋線故障時,故障線路與非故障線路間零序電流波形差異明顯,相似度低;母線故障時,非故障線路的零序電流波形在相同時刻所對應的相位基本相同,只是幅值略有差異,各線路的零序電流波形相似度較高。因此,在任意故障角下,均可采用文中方法實現故障選線。
1.3 時頻能量矩陣
對經HHT處理的各線路電流波形使用時頻譜帶通濾波法得到M(i=1,2,…,M)個不同頻帶的原始信號分量,將各頻帶原始信號分量按時間軸進行K等分,得到l個具有相同頻帶寬度和時間間隔的時頻小塊,對每個時段進行P等分。定義所有分量時頻小塊的能量為
(1)
式中:ail(m)為子頻帶i在時頻小塊l內m個數據點的幅值;Δt為每等分所占的時間。求出所有時頻小塊的幅值,可獲得各線路零序電流的時頻能量矩陣為
(2)
采用時頻譜帶通濾波法將各條線路的零序電流波形分解到16個不同的頻帶內,取頻帶寬度Δf=300 Hz,子頻帶的頻率范圍是[(i-1)Δf,iΔf](i=1,2,…,M),將每個子頻帶內的重構零序電流信號按時間軸等間距劃分為16個時間段,可以得到16×16個時頻小塊,據式(1)計算所有時頻小塊的能量值,即時頻能量矩陣中的元素。重構的某一子頻帶內零序電流信號分量及其時頻譜,如圖3所示。

圖3 Hilbert子頻帶時頻譜Fig. 3 Time-frequency spectrum for Hilbert sub-band
2 時頻能量矩陣相似度識別選線方法
2.1 相似度識別方法
設EA、EB分別是2條不同線路零序電流信號的時頻能量矩陣,則故障波形間的相似度ρAB為
(3)
式中,ρAB值越接近于1,即2條線路的故障波形越相似;ρAB值越小,說明2條線路的故障波形相似度越低。
2.2 接地故障選線判據
根據相似度矩陣求出線路i和其他線路間的綜合相似系數ki[16],與閾值kset比較判斷故障線路,經過多次仿真表明kset取值0.1。
發生單相接地故障選線判據如下:
1)如果線路i均有ki>kset,i=1,2,…,H,則是母線故障;
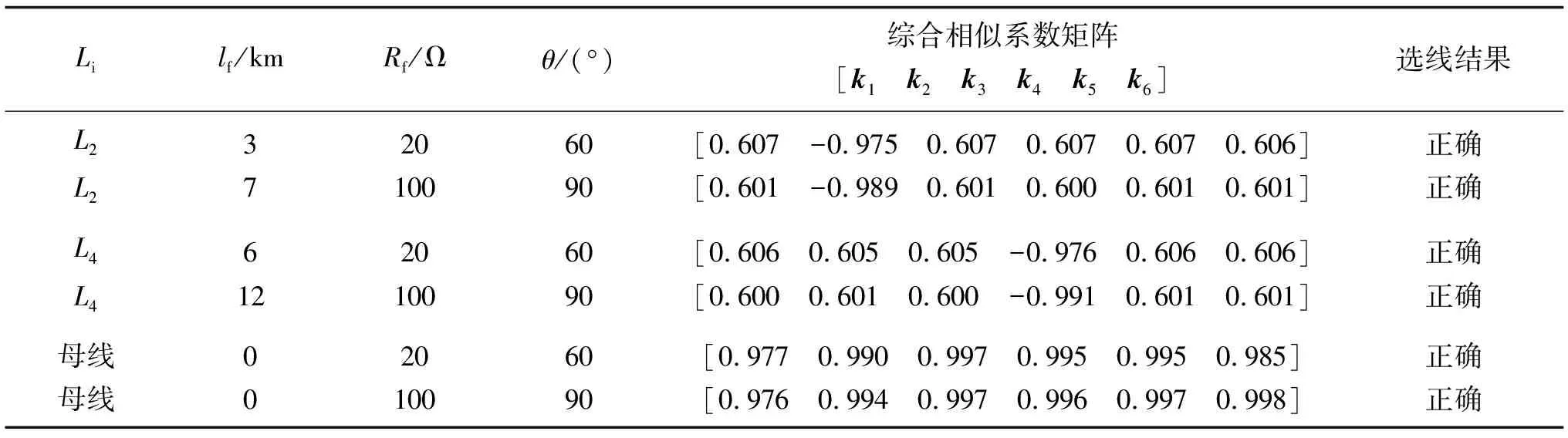
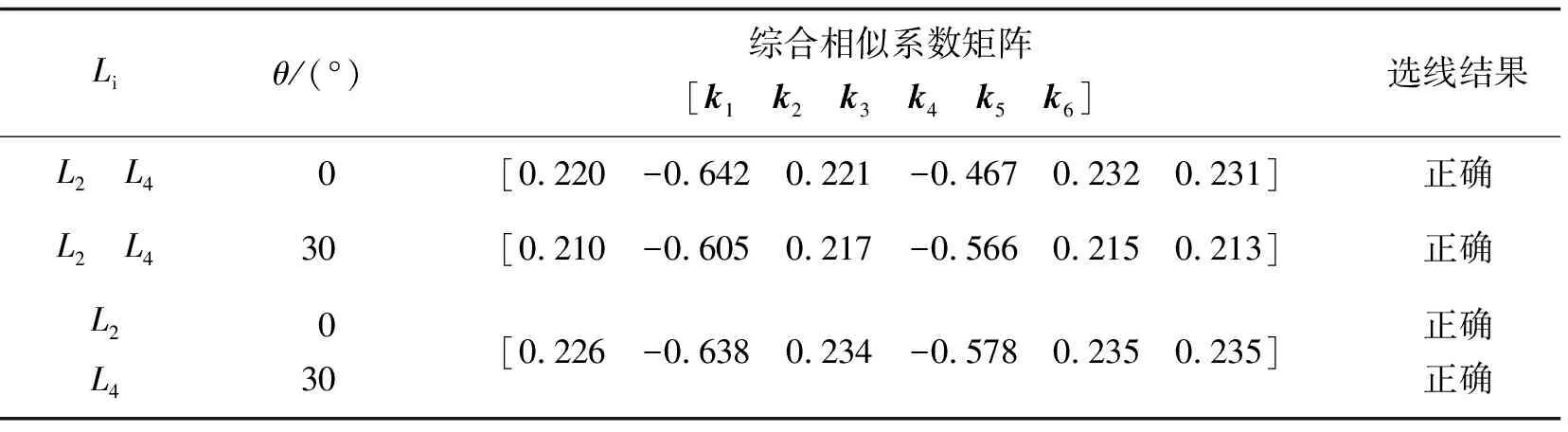
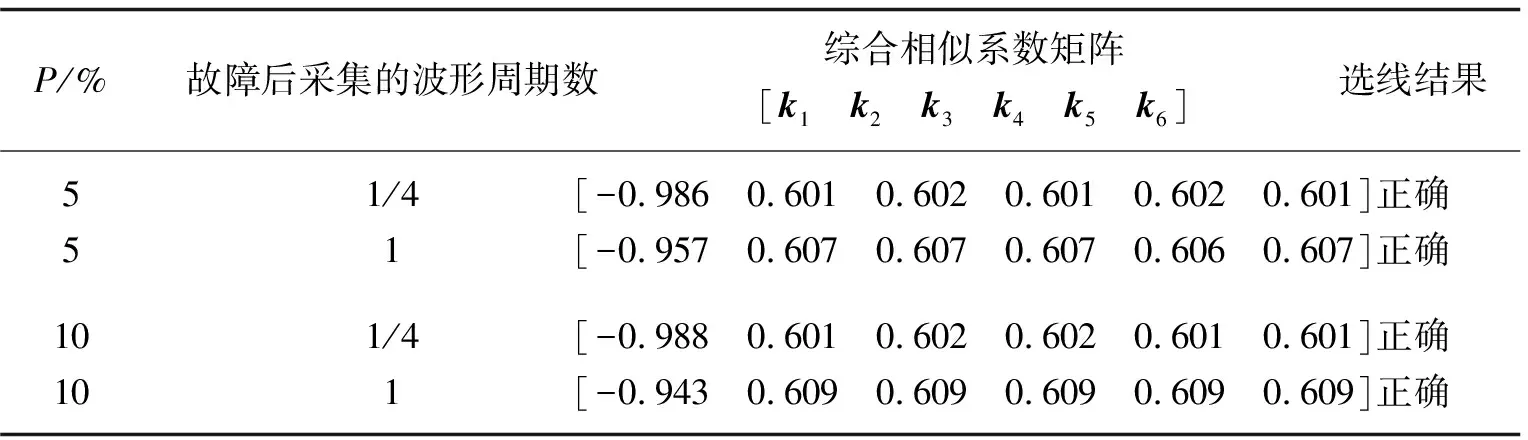
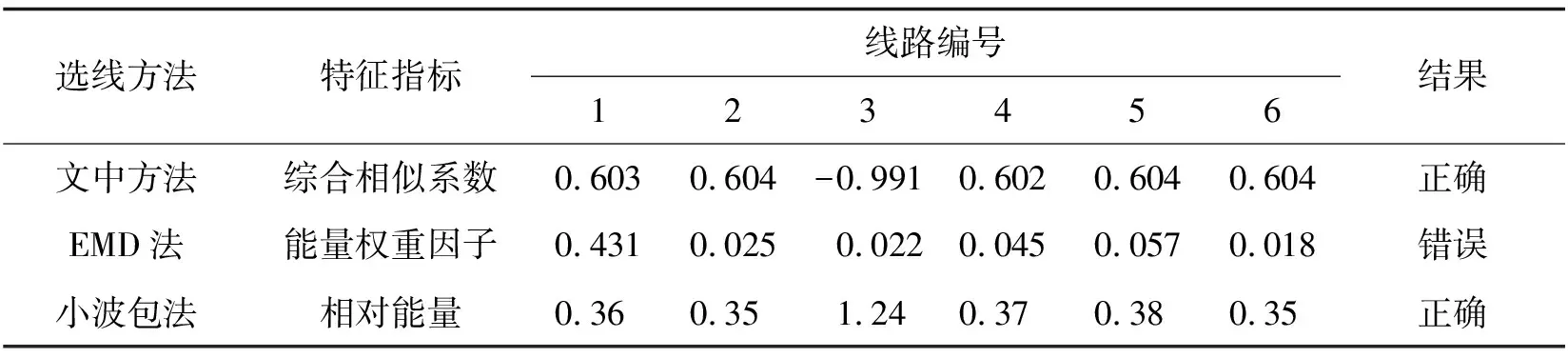
2)如果有ki 故障選線方法流程,如圖4所示。 圖4 故障選線方法流程Fig. 4 Flowchart of fault line detection 某地區110 kV/10 kV的變電站有L1~L4配電線路,其母線故障和饋線故障的采樣波形數據[17]分別如圖5和圖6所示,用來驗證文中方法的選線準確性。 圖5 母線故障的實測錄波波形Fig. 5 Measured recorded waveform of bus-bar fault 圖6 饋線L3故障的實測錄波波形Fig. 6 Measured recorded waveform of feeder L3 fault 3.1.1 母線故障 2013年2月10日,母線發生單相接地故障,計算每條線路零序電流的綜合相似系數,結果如下: k1=0.976,k2=0.995,k3=0.993,k4=0.995。 將綜合相似系數與閾值0.1比較,k1、k2、k3和k4的值均大于0.1,所以判定母線故障,判定結果與實際情況相符合。 3.1.2 饋線故障 2013年5月1日,饋線L3發生單相接地故障,計算每條線路零序電流的綜合相似系數,結果如下: k1=0.643,k2=0.651,k3=-0.975,k4=0.640。 將綜合相似系數與閾值0.1比較,k3 考慮線路類型對故障選線的影響,用MATLAB搭建纜線混合線路的諧振接地系統,其模型如圖7所示。圖中OL、CL分別為架空線路和電纜線路長度。消弧線圈的補償度取5%,電感L取值0.35 H,得到RL=0.03ωL=3.3 Ω,每條饋線的負荷大小是0.5+j0.25 MVA。仿真模型中主變壓器和饋線參數分別如表1和表2所示。 圖7 諧振接地系統仿真模型Fig. 7 Simulation model of resonant earthed system 表1 主變壓器的參數 表2 饋線參數 3.2.1 不同故障類型 為了驗證文中方法在不同故障情況下的選線有效性,改變饋線類型、故障位置、接地電阻和故障角幾種因素完成仿真分析。不同故障情況下接地故障的選線結果如表3所示。表中:Li是故障線路;lf是故障位置(故障點到母線的距離);Rf是接地電阻;θ是故障角; [k1k2k3k4k5k6] 是綜合相似系數矩陣。 表3 接地故障選線結果 由表3可知,當線路故障時,故障線路的綜合相似系數均小于閾值kset(kset=0.1);當母線故障時,所有線路的綜合相似系數均大于0.1,不同條件下均正確選線。 3.2.2 噪聲干擾 設置線路L1和線路L3發生單相接地故障,故障信號中加入高斯白噪聲(信噪比為30 dB)時,仿真結果如表4所示。 表4 高斯白噪聲影響的選線結果 由表4可知,該方法在噪聲干擾下準確選線,抗干擾能力強。假設線路3在故障角為90°時,不對零序電流作HHT分解,得到的直接計算結果是[0.537 0.536 -0.947 0.528 0.553 0.543],選線結果正確但選線裕度較低,適應性不強。 3.2.3 兩點接地故障 設置線路L2在lf=7 km和線路L4在lf=5 km處發生B相接地故障,接地電阻是20 Ω,其仿真選線結果如表5所示。結果表明,此方法在線路同時和不同時發生兩點接地故障均正確選線,適應性較好。 表5 兩點接地故障時的選線結果 3.2.4 不同暫態時間范圍 當消弧線圈處于過補償狀態時,諧振接地系統發生單相接地故障時零序電流減小,其減小量與補償度有關,而且零序電流波形特征的持續時間短暫,因此,設置線路L1末端在故障角接近0,接地電阻是2 kΩ時發生接地故障,選用不同補償度p下,不同暫態時間范圍內的零序電流波形,其仿真選線結果如表6所示。由表6可知,此方法在消弧線圈處于過補償狀態,即使零序電流波形特征的持續時間短暫,仍可正確選線。 表6 不同暫態時間范圍的故障選線結果 假設故障線路是L3,在接地電阻Rf=20 Ω、故障位置lf=3 km和故障角θ=0時,故障信號中加入高斯白噪聲(信噪比為30 dB)進行仿真,分別用文中方法、基于EMD的選線方法[7]和基于小波包的選線方法[8]進行選線,結果如表7所示。 表7 故障選線結果 由表7可知,在惡劣的故障環境下零序電流幅值會受到影響而減小,影響故障特征提取,引起基于EMD選線方法失誤。而基于小波包的選線方法雖然選線正確,但小波包選線方法中的小波基函數的確定具有主觀性,選線效果依賴于小波基函數的確定,在惡劣復雜的故障工況下會出現誤選。文中所用HHT自適應分解零序電流,利用時頻帶通濾波法重構零序電流,解決了HHT分解故障信號存在的模態混疊問題,實現正確的故障選線。 利用故障后各線路零序電流波形圖像的相似度,結合各線路電流波形的時頻能量矩陣,提出一種配電線路的接地故障選線新方法。 1)采集零序電流波形數據實現接地故障選線,充分利用幅值和極性等故障信息,克服了單一型選線依據的片面性所造成的選線錯誤問題。 2)該方法有效放大了故障電流特征,可以區分母線故障和饋線故障,在外界噪聲干擾和發生兩點接地故障情況下其適應性較好。 3)采用復雜的時頻能量矩陣相似度實現故障選線,解決了僅利用波形相似度選線需提取整個頻帶故障信號特征時所忽略的故障信號時變性問題。
3 算例分析
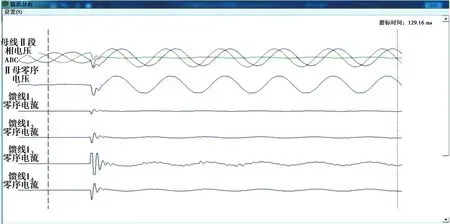
3.1 算例驗證

3.2 方法適應性分析




3.3 方法優越性比較
4 結 論

