高壓渦輪導(dǎo)葉傳熱數(shù)值計(jì)算與分析

王建華，葛寧

(南京航空航天大學(xué) 能源與動(dòng)力學(xué)院，江蘇 南京 210016)

0 引言

在現(xiàn)代燃?xì)鉁u輪發(fā)動(dòng)機(jī)中，高壓渦輪導(dǎo)葉與燃?xì)鉄峤粨Q率最高。因渦輪進(jìn)口溫度遠(yuǎn)超過(guò)金屬葉片的熔點(diǎn)溫度，故必需大量使用冷卻氣體，這就要求在設(shè)計(jì)過(guò)程中準(zhǔn)確地預(yù)測(cè)渦輪葉片表面溫度分布。丁林[1]搭建了渦輪葉片測(cè)溫平臺(tái)，利用光學(xué)掃描和輻射測(cè)溫方法對(duì)葉片表面溫度分布進(jìn)行測(cè)量。近年來(lái)，研究人員對(duì)氣熱耦合方法進(jìn)行了廣泛研究。LUO J等[2]研究了渦輪導(dǎo)葉在3種典型工況下的氣動(dòng)和傳熱特性，采用不同的湍流模型計(jì)算分析了葉中截面處溫度分布和外換熱系數(shù)分布。褚云會(huì)等[3]對(duì)跨音速渦輪數(shù)值模擬，分析了網(wǎng)格量和湍流模型對(duì)計(jì)算結(jié)果的影響。CROCE G[4]將開(kāi)發(fā)的程序和商業(yè)軟件進(jìn)行了耦合，即流體域和固體域使用不同的網(wǎng)格，通過(guò)插值程序?qū)⒘鞴探唤用嫔系男畔⑦M(jìn)行傳遞。郭兆元等[5]采用耦合和非耦合方式對(duì)單級(jí)渦輪機(jī)葉片數(shù)值計(jì)算，表明兩種計(jì)算方法對(duì)流場(chǎng)結(jié)構(gòu)影響不大，只有耦合計(jì)算能準(zhǔn)確地預(yù)測(cè)溫度分布。雖然耦合計(jì)算正確地設(shè)置了流固交接面上邊界條件，但是，在計(jì)算復(fù)雜的內(nèi)部冷卻結(jié)構(gòu)時(shí)，這種方法在工程應(yīng)用上受到限制。因此，在研究冷卻問(wèn)題時(shí)，有學(xué)者提出用外換熱系數(shù)定量描述對(duì)流換熱現(xiàn)象，這也是工程上初步設(shè)計(jì)冷卻系統(tǒng)的常用方法。

本文首先在典型工況下對(duì)C3X計(jì)算域進(jìn)行數(shù)值敏感性驗(yàn)證。然后采用非耦合方法計(jì)算分析了壁面溫度對(duì)外換熱系數(shù)(HTC)的影響。采用耦合方法對(duì)比了不同湍流模型下HTC分布。最后對(duì)改進(jìn)的換熱量預(yù)測(cè)方法進(jìn)行可行性分析并對(duì)比不同計(jì)算方法下的HTC。

1 求解方法及驗(yàn)證

采用課題組自主研發(fā)的NUAA-TURBO三維數(shù)值求解器和ANSYS-CFX求解器求解雷諾平均Navier-Stokes方程(RANS)。通過(guò)Numeca對(duì)C3X葉型建立計(jì)算域網(wǎng)格，如圖1所示，其中進(jìn)、出口為H型網(wǎng)格，葉片表面建立O型網(wǎng)格。由于熱邊界層受網(wǎng)格影響較大，為了正確模擬傳熱，葉片表面的y+值<1，網(wǎng)格節(jié)點(diǎn)數(shù)達(dá)2×107。計(jì)算域邊界條件如下：來(lái)流總壓P0=3.218×105Pa，來(lái)流總溫T0in=783K，出口馬赫數(shù)Maisout=0.89，湍動(dòng)量Tu=8.3%，湍流長(zhǎng)度尺度為0.005m。

圖1 計(jì)算域網(wǎng)格及邊界條件

1.1 網(wǎng)格無(wú)關(guān)性驗(yàn)證

首先改變沿葉片輪廓周圍邊界層中的O型網(wǎng)格節(jié)點(diǎn)，使用NUAA-TURBO求解器來(lái)進(jìn)行網(wǎng)格無(wú)關(guān)性驗(yàn)證。在保證離壁距離相同的情況下，比較了3種不同的網(wǎng)格節(jié)點(diǎn)。如圖2所示，在溫度比TR=Tw/T0in=0.65時(shí)，計(jì)算了30、40和50個(gè)節(jié)點(diǎn)下葉片表面的無(wú)量綱換熱量q/qref分布。無(wú)量綱換熱量的計(jì)算方法見(jiàn)式(1)，換熱量q通過(guò)壁面附近流體分子之間導(dǎo)熱計(jì)算，即q=-k(?T/?n)。C為葉片軸向弦長(zhǎng)，k為進(jìn)口溫度條件下的導(dǎo)熱系數(shù)。從整體上看，3種網(wǎng)格節(jié)點(diǎn)下的計(jì)算結(jié)果差異很小，在之后的計(jì)算中選擇網(wǎng)格節(jié)點(diǎn)為40。

(1)

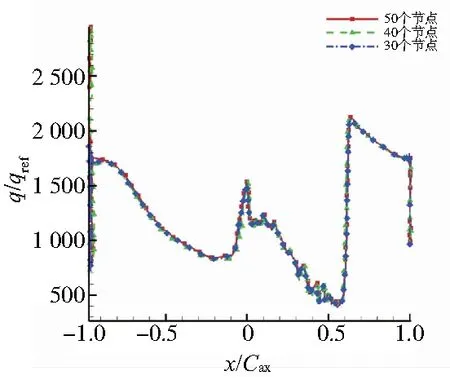
圖2 TR=0.65時(shí)不同邊界層節(jié)點(diǎn)HTC分布

1.2 非耦合計(jì)算

通過(guò)NUAA-TURBO求解器的定量計(jì)算來(lái)分析TR對(duì)HTC的影響。計(jì)算域的邊界條件如上所述，在不同工況下，僅僅改變壁面溫度邊界條件。假設(shè)空氣為理想氣體，理想氣體定律和薩瑟蘭黏性定律來(lái)求解氣體的狀態(tài)和熱物理性質(zhì)。從圖3中可以清楚地看出葉片壁面溫度對(duì)HTC的影響。在葉片尾緣的相同位置處，在TR=0.60情況下的HTC比TR=0.95情況下高30%左右。同時(shí)，在葉片前緣的駐點(diǎn)區(qū)域，TR對(duì)HTC的影響不如尾緣區(qū)域明顯。這也表明上游歷史效應(yīng)對(duì)邊界層的影響。在葉片前緣附近，由于邊界層剛形成，對(duì)壁面的溫度影響較小，但是，隨著邊界層在葉片表面的發(fā)展，相比于邊界層外部流動(dòng)，溫度不同的流體在邊界層內(nèi)部逐漸積累并且不斷影響壁面溫度。這表明當(dāng)?shù)乇诿鏈囟葪l件影響HTC，同時(shí)受冷卻表面的外換熱系數(shù)還與上游邊界層發(fā)展歷程相關(guān)。

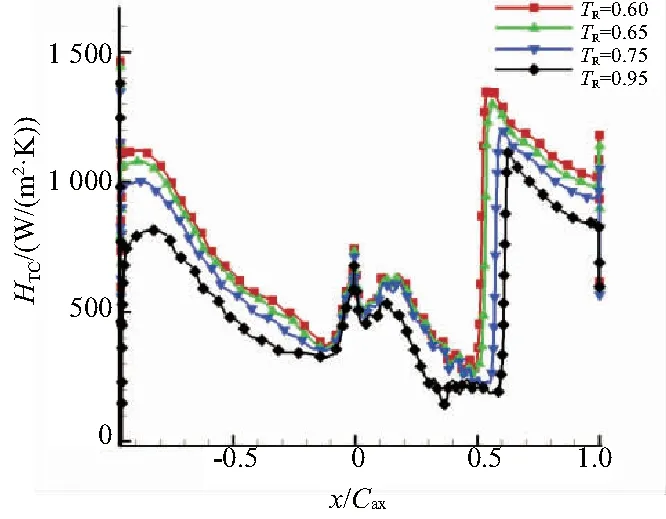
圖3 外換熱系數(shù)HTC依賴于TR

1.3 耦合計(jì)算

在非耦合計(jì)算中只是考慮外部氣動(dòng)影響。正如在數(shù)值計(jì)算時(shí)，都是給定等溫邊界條件，這就改變了葉片表面和流體域之間的真實(shí)交界面邊界條件。為了排除這種任意邊界條件的影響，采用CFX求解器中的熱-固耦合模型數(shù)值計(jì)算。圖4給出了耦合計(jì)算域，外部流體域與非耦合計(jì)算下的邊界條件一致，葉片內(nèi)部固體域材料選擇熱導(dǎo)率較低的ASTM310型不銹鋼，在葉片內(nèi)部有10個(gè)冷卻通道，每個(gè)冷卻通道進(jìn)口給定半徑、進(jìn)口質(zhì)量流量、進(jìn)口靜溫和湍流度。這里選擇文獻(xiàn)[6]中4422工況。

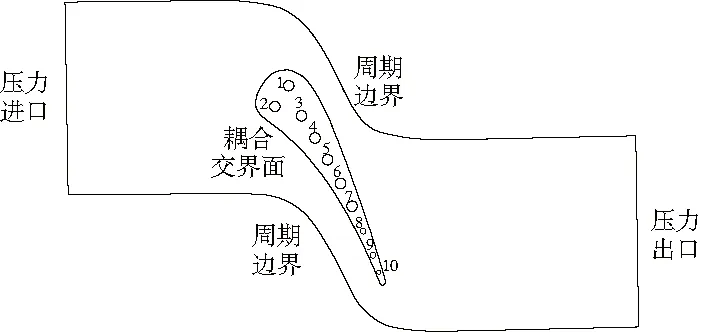
圖4 耦合計(jì)算域

圖5顯示了不同湍流模型下，葉片表面無(wú)量綱靜壓分布，計(jì)算結(jié)果表明湍流模型對(duì)氣動(dòng)特性的影響較小。在壓力面，從葉片前緣到x/Cax=-0.5附近，壓力幾乎保持不變，這個(gè)階段流體加速緩慢，葉片表面沒(méi)有分離，邊界層內(nèi)的靜壓梯度為0，葉片表面的壓力分布受湍流模型的影響很小。從壓力面中部到尾緣附近，壓差增大，流體急劇加速。在吸力面，從前緣到x/Cax=0.4附近，靜壓快速下降到進(jìn)口壓力的一半。隨后流體開(kāi)始減速，到尾緣附近，流體又經(jīng)歷了緩慢地加速的過(guò)程。

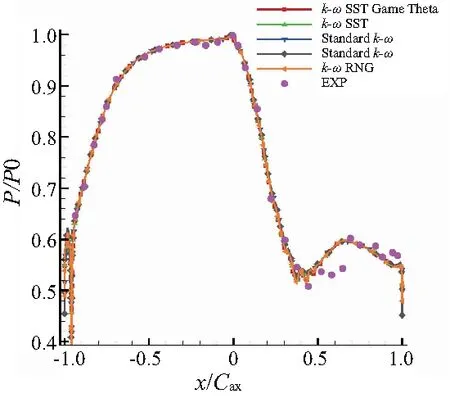
圖5 不同湍流模型下葉片表面靜壓分布

如圖6所示，不同湍流模型下?lián)Q熱系數(shù)與實(shí)驗(yàn)值對(duì)比。從整體上看，邊界層內(nèi)部的轉(zhuǎn)捩流動(dòng)對(duì)HTC有較大影響。在吸力面前緣沿葉片表面下游，不同湍流模型對(duì)外換熱系數(shù)的預(yù)測(cè)都有不同程度的偏差。高雷諾數(shù)湍流模型(k-ε類)主要模擬湍流狀態(tài)，使用半經(jīng)驗(yàn)公式簡(jiǎn)化邊界層流動(dòng)，計(jì)算所得的湍流強(qiáng)度比較高，同時(shí)在吸力面前緣附近，激波-附面層相互干擾的現(xiàn)象極為明顯，對(duì)計(jì)算結(jié)果有較大影響。盡管低雷諾數(shù)湍流模型(k-ω類)計(jì)算所得的湍流強(qiáng)度較低，但是仍然反映邊界層內(nèi)部的湍動(dòng)特性。對(duì)于吸力面前緣附近的層流區(qū)域，無(wú)法準(zhǔn)確地分辨。如果在k-ωSST湍流模型上使用轉(zhuǎn)捩模型，預(yù)測(cè)的HTC與實(shí)驗(yàn)值吻合較好。

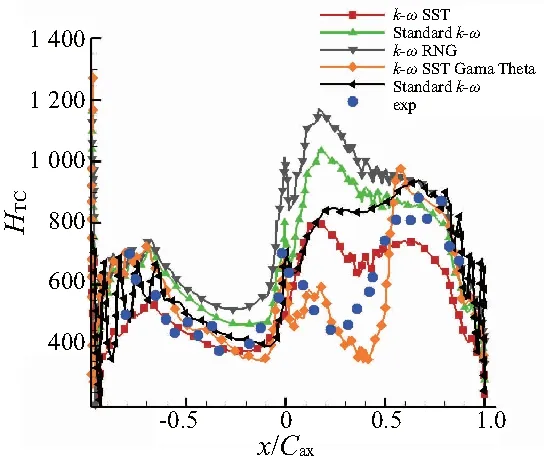
圖6 不同湍流模型下HTC對(duì)比

2 非線性方法可行性分析

在典型非耦合計(jì)算中假設(shè)：氣動(dòng)性能決定換熱性能。對(duì)于給定的葉型結(jié)構(gòu)和流動(dòng)條件，在牛頓冷卻定律q=h(T-Taw)中，有兩個(gè)由氣動(dòng)決定的未知量(h，Taw)。由于這兩個(gè)未知量不受壁溫影響，h值能正確地表示為每一點(diǎn)處的曲線斜率，可將其改寫成式(2)的形式。

(2)

當(dāng)q與Tw呈現(xiàn)明顯的非線性關(guān)系時(shí)，曲線斜率表現(xiàn)為在當(dāng)?shù)刈兓Ｊ?2)改寫成式(3)。此時(shí)式(3)中的外換熱系數(shù)h可以解釋為微分算子dq/dTw的有限差分近似，對(duì)于給定的壁溫Tw，在極小的溫差ΔT范圍內(nèi)，曲線的局部斜率能正確地表示外換熱系數(shù)。

(3)

為了確定式(3)中ΔT的取值大小，在TR=0.70條件下，選取3K、5K和10K進(jìn)行驗(yàn)證研究。為了在圖中顯示清晰，去掉了尾緣回流區(qū)域內(nèi)和轉(zhuǎn)捩附近HTC分布的峰值點(diǎn)。如圖7所示，在所選取的3個(gè)溫差下，計(jì)算所得外換熱系數(shù)基本相同，因此，在下面兩點(diǎn)法的計(jì)算中選擇5K。

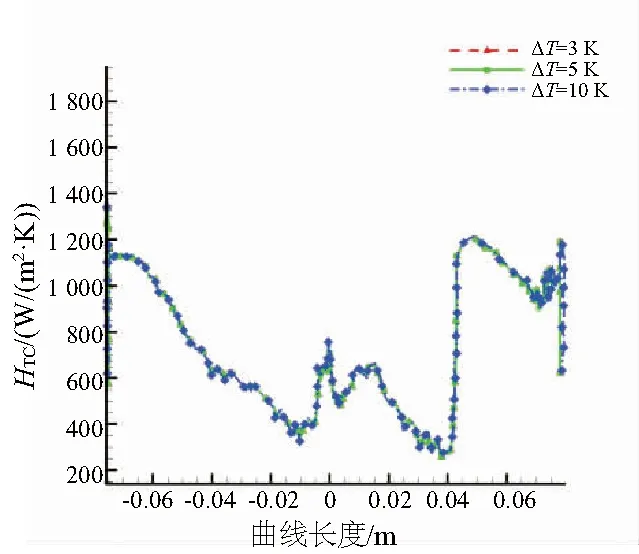
圖7 3種溫差下葉中截面外換熱系數(shù)分布

根據(jù)非耦合計(jì)算結(jié)果中的分析，非線性方法主要考慮了HTC與Tw呈現(xiàn)線性關(guān)系，即HTC=h0+h1Tw。不考慮絕熱壁溫隨壁面溫度的變化。具體表達(dá)式如下：

q=(h0+h1Tw)(Tw-Taw)

(4)

在3個(gè)壁溫下，求解式(4)中的未知變量h0,h1和Taw。這些未知變量確定后，就可以根據(jù)式(4)確定未知Tw下的換熱量分布以及對(duì)應(yīng)壁面溫度下的HTC。未知變量也是葉片表面上的每個(gè)網(wǎng)格點(diǎn)的常數(shù)。這種當(dāng)?shù)匦Ｕ椒ㄅc相關(guān)經(jīng)驗(yàn)關(guān)系式有明顯地區(qū)別。求解葉片表面HTC分布的常規(guī)做法是需要不同壁溫下兩個(gè)CFD計(jì)算解。該方法只需要3個(gè)CFD解，計(jì)算成本低，而預(yù)測(cè)精度得到質(zhì)的提高。

在溫度比為0.95、0.75和0.65條件下，使用NUAA-TURBO求解器得到每個(gè)網(wǎng)格點(diǎn)的換熱量來(lái)求解式(4)。用非線性方法可以預(yù)測(cè)溫度比為0.6～0.95范圍內(nèi)的換熱量。圖8比較了非線性方法的計(jì)算結(jié)果與數(shù)值計(jì)算結(jié)果。這種方法可確保在整個(gè)Tw范圍內(nèi)，預(yù)測(cè)結(jié)果與CFD數(shù)值計(jì)算結(jié)果的匹配非常好。為了突出HTC獨(dú)立于Tw的假設(shè)所帶來(lái)的誤差，還使用傳統(tǒng)的兩點(diǎn)法預(yù)測(cè)了溫度比分別為0.7、0.8和0.9下的換熱量。如圖9所示，結(jié)果表明兩點(diǎn)法無(wú)法體現(xiàn)HTC隨壁面溫度的變化，從而在換熱量的預(yù)測(cè)中帶來(lái)誤差。

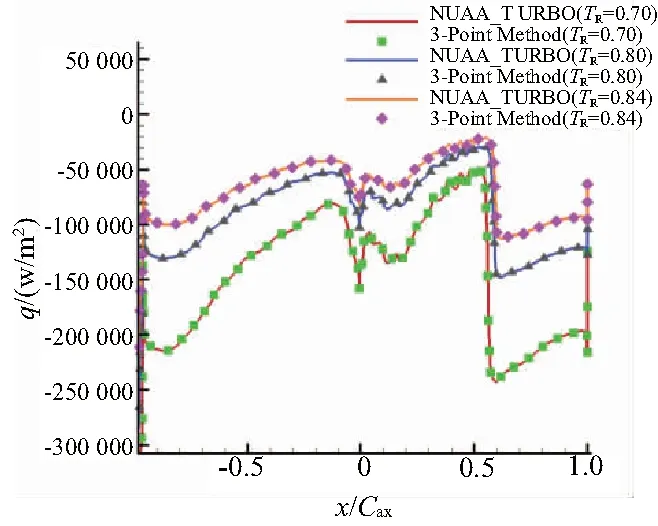
圖8 CFD解與非線性方法的換熱量對(duì)比

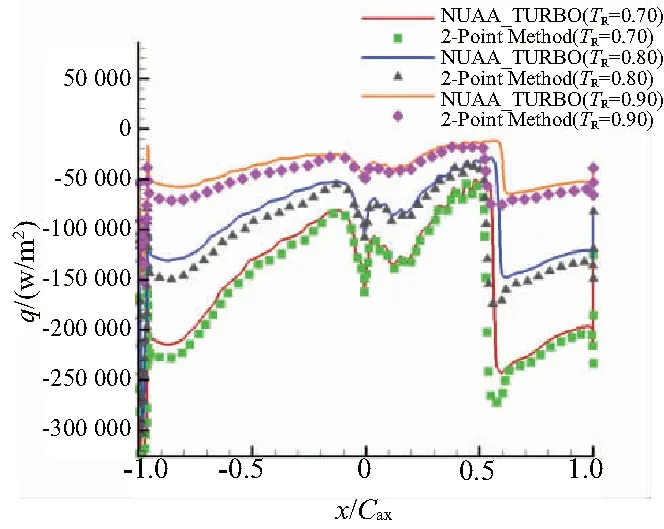
圖9 CFD解與兩點(diǎn)法的換熱量對(duì)比

3 外換熱系數(shù)分布

圖10對(duì)比了葉片表面平均溫度TR=0.84情況下，兩點(diǎn)法、非線性方法以及耦合計(jì)算下的HTC分布。在校正過(guò)程中，兩點(diǎn)法在轉(zhuǎn)捩附近出現(xiàn)了尖峰值，與兩點(diǎn)法相比，非線性方法預(yù)測(cè)的外換熱系數(shù)值更加穩(wěn)定，這種穩(wěn)定性主要是對(duì)不同壁面穩(wěn)定范圍內(nèi)的多點(diǎn)曲線擬合，而傳統(tǒng)的兩點(diǎn)法只是基于單個(gè)壁面溫度上局部區(qū)域內(nèi)的差分近似。如圖10所示，非線性方法在轉(zhuǎn)捩位置處與實(shí)驗(yàn)值和耦合計(jì)算有些誤差，從整體上看，可以較為準(zhǔn)確地預(yù)測(cè)外換熱系數(shù)。

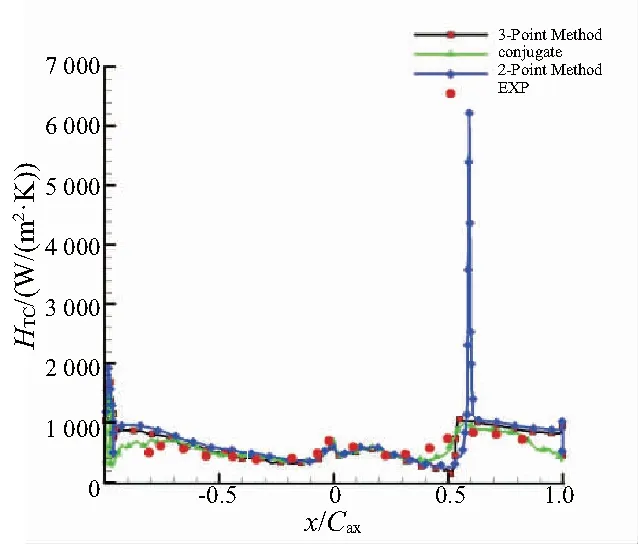
圖10 TR=0.84條件下外換熱系數(shù)分布對(duì)比

4 結(jié)語(yǔ)

本文以典型高壓渦輪平面葉柵C3X為例，采用NUAA-TURBO求解器和CFX求解器主要研究高壓渦輪葉片外換熱系數(shù)與壁溫的關(guān)系。得出以下結(jié)論：

1)非耦合計(jì)算時(shí)，壁溫對(duì)葉片前緣處HTC的影響較小，但是在葉片尾緣有明顯的非線性。特別地，在TR=0.60與TR=0.95兩種情況下，HTC相差達(dá)到30%左右。耦合計(jì)算時(shí)，帶轉(zhuǎn)捩的k-ωSST湍流模型能較為準(zhǔn)確地預(yù)測(cè)外換熱系數(shù)分布。

2)基于牛頓冷卻定律的非線性形式，采用非線性方法來(lái)計(jì)算不同壁溫下外換熱系數(shù)。與傳統(tǒng)方法相比，可以有效地對(duì)HTC-Tw依賴性進(jìn)行校正。非線性方法是在給定壁面溫度的情況下獲得外換熱系數(shù)，這種基于當(dāng)?shù)氐亩皇侨值男Ｕ椒ǎ岣吡擞?jì)算精度。