基于旋量理論的7自由度機械臂運動學建模與分析

李冠琦，武建德，李瑞琴

(中北大學 機械工程學院，山西 太原 030051)

0 引言

機械臂是機器人技術領域中應用最為廣泛的自動化裝置，在工業制造、醫療康復等領域都有其應用實例，擬人化機械臂技術也逐漸成熟[1-4]。匹茲堡大學生物醫學團隊在BCI機械臂假肢里引入實時觸覺反饋，使完成任務的時間減少一半。波士頓動力開發Stretch移動式7R機械臂已應用于倉庫運輸。

20世紀80年代學者們開始討論將旋轉軸從數學中引入機器人研究的可行性，旋量理論[5-9]日益成熟，然而對其的應用介紹卻鮮見報道。本文建模7自由度串聯機械臂，著重對螺旋軸這一單位矢量在運動學的應用加以詳細描述。

6自由度逆解有通用公式，7R逆解包含32個實根，出現虛空間或自運動歧。7R逆解可結合Newton-Raphson數值迭代法求解[10]。

使用Matlab進行正解中的化簡與直接展開等運算過程的比較，并且同時使用開源Python對結果進行比較。使用基于空間(space簡稱s)坐標系的空間雅可比矩陣，找出數值迭代法求逆解的適用范圍，基于正解的前提下，驗證逆解的準確性。

1 旋量理論

螺旋(旋量——旋轉向量)理論在正運動學中的應用。

1.1 M矩陣(0位置、起始位置)

M矩陣為當所有的關節轉角都為0的時候，操作空間坐標系(body簡稱b)在s坐標系中的位置和姿態矩陣。

1.2 旋轉向量與指數積公式

(1)

(2)

T07=eS7θ7M

(3)

特殊正交群是所有有效的3×3旋轉矩陣的集合群SO(3)：包括R、ω、eωθ。特殊的歐幾里得集合群或剛體運動群或R3中的同質變換矩陣Se(3)表示位姿：包括M、eSθ、T07。

(4)

式(4)中，可利用特性ω3=-ω來化簡，且eωθ有Rodrigues公式：

f(θ)=Iθ+(1-cosθ)ω+(θ-sinθ)ω2

(5)

eωθ=I+sinθω+(1-cosθ)ω2

(6)

依次解鎖一個角度，往前代值，得到

T07=eS1θ1…eS7θ7M

(7)

2 數值法逆解

使用非線性尋根的Newton-Raphson方法，有尋根、不存在根時尋找近似解、存在多個解時尋找最優解的優勢。給定一個初始值，然后代入迭代式求解直到出現誤差范圍內的解。

設正向運動學函數為f(θd)，末端執行器的位置向量為ν，非線性尋根Newton-Raphson是找到目標函數的解。幾何視角如圖1所示；式(8)是解析視角。式(9)-式(11)是計算雅可比矩陣。

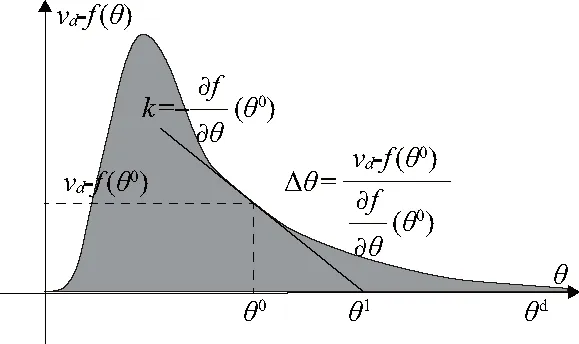
圖1 迭代法幾何過程

Δθ=J-1(θ0)[vd-f(θi)]

(8)

(9)

(10)

(11)

式中*為其伴隨矩陣。

對這種算法的進一步改進：

1)末端執行器的位置描述f(θd)變更為正運動學計算出的矩陣T07。

3)引進偽逆矩陣J?避免求解奇異時無解的情況。在Matlab里編程為pinv(J)。

當前基于b坐標系，變換為基于s坐標系：

(12)

(13)

式中：Tsb是坐標轉移矩陣；*為求其伴隨矩陣。

改進算法的流程圖如圖2所示。

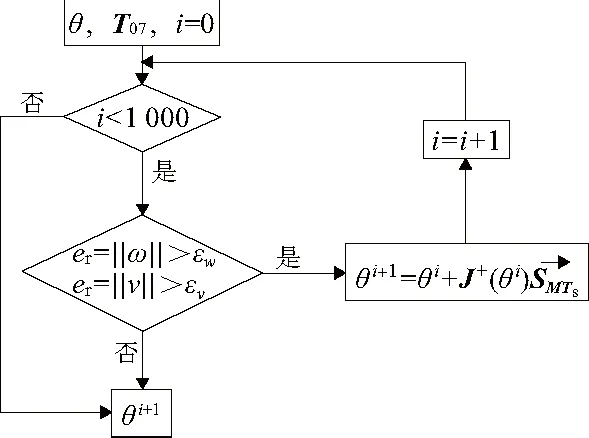
圖2 改進的數值迭代法流程圖

3 驗證正逆解

3.1 正運動學方程

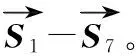
(14)

(15)

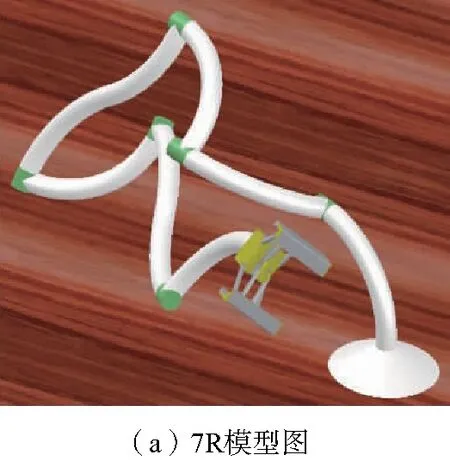
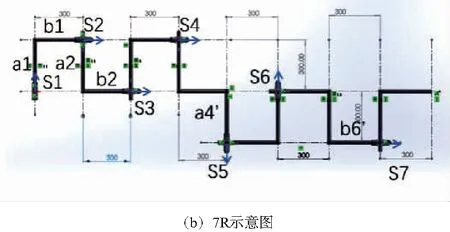
圖3 三維模型圖及7R示意圖

根據式(3)，使用矩陣分塊后化簡的運算過程，編程并計算結果。

(16)

根據式(3)，發現將矩陣指數直接泰勒展開(采用了3種計算方法：Pada法、特征值法、6次的泰勒展開)得出的結果雖然一致，但是它是虛數形式，增加了計算量。結果：

(17)

使用先進行矩陣分塊然后利用特性化簡的運算方法，該結果更準確、后期的運算量更小。代入式(7)，使用該方法分別在Matlab和Python中運算，得出的結果一致：

r1=150s1234-5-1 350s12347-300s123-675s123457-6-

675s123467-5-150s12345-1 350s1234-7+600s1234+300s12+

675s12345-6-7+675s12346-5-7-300s1+750s12345-6-750s12346-5

r2=150c1234-5+1 350c12347+300c123+675c123457-6+

675c123467-5-150c1234-5+1 350c1234-7-600c1234-300c12-

675c12345-6-7-675c12346-5-7+300c1-750c12345-6+750c12346-5

r3=2 700s7c5s6-s5c6-1 500s5s6-c5(1 500c6-1 500)-

1 200c5+1 200

3.2 逆運動學方程

1)第一次驗證

設初始位置為正解的0位置，轉動角度為θlist。

[3.142;1.571;1.047;0.785;0.628;0.524;0.449]

給逆解的初始值[3,1.5,1,0.6,0.5,0.4,0.3]。解得[3.161,1.563,1.059,0.762,0.628,0.523,0.449]。

2)第二次驗證

因發現誤差較大：1)改用角度制；2)迭代次數增加到1 000次；3)精度調整為eω<0.000 1，ev<0.000 1。經過多組數據實驗發現，相差3°以內，位置完全重現；相差10°以內，第一角度有0.1°的偏差；相差15°以上的逆運算，第一個角度有1°以上的偏差。所以，該方法求逆解有完全重現的適用范圍，需要把初始解猜測在真實解的附近15°以內(表1)。

表1 正逆解互相驗證 單位：(°)

4 結語

本文重點介紹了如何使用形如螺旋樓梯的轉向量計算正逆解。結合旋量與Newton-Raphson數值法求逆解。為涵蓋轉動機構可能出現的問題，采用目前串聯機構中最復雜的7R機構并且使機構盡可能復雜，但是設計中沒有涵蓋helical螺旋和cylindrical圓筒等機構。在比較了不同的運算方法后，計算正解，得出先將矩陣分塊、再利用特性化簡的方法更好的結論。在計算逆解的過程中，發現當初始猜測的第一個角度超過真實解20°，Newton-Raphson數值法不會重現正解。驗證結果表明旋量形式美觀，建模快捷，編程明了，適用于機械臂中的串聯機構、并聯機構、轉動關節、平動關節、螺旋關節等的運動學、動力學特性建模和分析。