采摘機械臂的PSO-RBF神經網絡自適應控制

董中華，陳鵬飛，李亞龍

(蘭州理工大學 機電工程學院，甘肅 蘭州 730050)

0 引言

機械臂是一種多輸入、多輸出且具有時變性、時滯性和高度耦合性的復雜非線性系統[1]。機器臂系統的不確定性可能會導致依據該模型構造的控制器性能降低，甚至不穩定。在控制器設計時，很多控制策略都會有局限性，這將會對機械臂系統輸出跟蹤期望軌跡的實現帶來巨大影響。因此機械臂系統中存在不確定項難以避免地會導致系統的性能大大降低[2]。神經網絡應用在機械臂運動控制中，可以處理機械臂系統模型中的不確定性，還能對它進行實時控制[3]。

由于徑向基神經網絡結構簡單,具有較強的泛化性能，近年來，很多人對RBF神經網絡在機械臂控制的方向進行了研究，極大地推動了機械臂的RBF神經網絡控制發展的進程。一些研究人員運用RBF神經網絡的特性做出了自適應控制[4-5]。其中一部分研究人員在此基礎上結合魯棒控制，形成神經網絡魯棒自適應控制[6-7]。一些研究人員將RBF神經網絡控制和模糊控制相結合，結合二者的優點組成模糊神經網絡控制[8-9]。隨著現代智能優化算法的興起，如遺傳算法(GA)、進化策略(ES)和粒子群算法(PSO)等，一些研究人員使用GA優化神經網絡的參數，并設計了GA-RBF神經網絡控制[10-11]。而PSO相對于GA而言，不需要編碼，沒有交叉和變異操作，粒子只是通過內部速度進行更新，因此原理更簡單、參數更少、實現更容易。一些研究人員使用PSO結合RBF神經網絡在預測方面的研究很深入，但在機械臂控制方面不多。文獻[12-13]僅在自校正控制和逆運動方面進行了研究。

本文在文獻[11]的GA-RBF控制方法中得到啟發，采用了另一種現代智能算法(PSO)來替代GA，設計了PSO-RBF控制方法。

1 機械臂系統問題描述

由于機械臂的每個關節就是一個輸入，也是一個輸出，而且關節與關節之間又存在著擾動，耦合關系復雜。所以機械臂的系統模型很難精確獲得。通常是用它的靜止模型作為名義模型，再通過反饋進行自適應調節，以達到精確的軌跡跟蹤控制。

假設被控對象為n關節機械臂，其動態方程為：

(1)

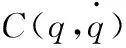
(2)

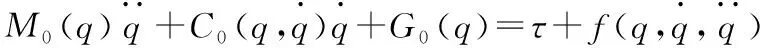
在計算力矩控制法中，采用名義模型，設計控制律為

(3)

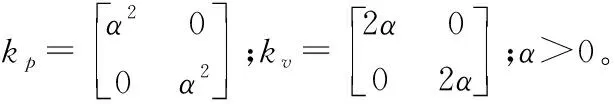
將式(2)代入式(1)，可得誤差系統為

(4)

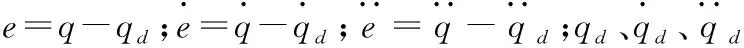
在實際工程中，f(·)通常是未知的，需要估計f(·)并對其補償。利用RBF神經網絡逼近任意非線性函數的特性逼近f(·)，并對其進行補償，就可以達到想要的控制效果。

2 PSO-RBF神經網絡

2.1 RBF神經網絡逼近原理

采用RBF網絡逼近f(·)，其算法為

(5)

y=wTh(x)

(6)

其中：x是RBF神經網絡的輸入；w是神經網絡的權值；h=[h1,h2,…,hm]T是高斯函數的輸出。

給定一個很小的數ε使得RBF逼近公式(3)中的f(·)，有如下公式：

(7)

定義逼近誤差為

(8)

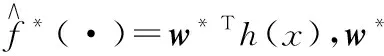
當逼近誤差η無限趨近于0，則系統的不確定項被有效地逼近，通過補償可以保證準確的控制。

2.2 PSO優化原理

粒子群優化算法屬于進化算法的一種，和模擬退火算法相似，它也是從隨機解出發，通過迭代尋找最優解。

首先，粒子群算法將優化問題的解當作搜索空間中的一只鳥，在搜索的空間中以一定的速度飛行，速度大小根據它自身以及同伴的飛行經驗進行動態調整。鳥被想象成為一個沒有質量和體積的粒子，第i個速度粒子在n維空間里的位置表示為向量xi=(xi1,xi2,…,xin)，飛行速度表示為向量vi=(vi1,vi2,…,vin)。每個粒子都有一個由被優化函數所決定的適應值，而且知道自己到目前為止所發現的最好位置xpi=(xpi1,xpi2,…,xpin)。此外，每個粒子還知道到目前為止鄰域粒子所發現的最好位置xg=(xg1,xg2,…,xgn)。PSO算法是一種基于迭代的優化算法，第t1次迭代時，粒子將根據自身的經驗和同伴的經驗來決定下一步運動速度和位置。基本PSO算法的粒子位置和速度的更新公式如下：

vij(t+1)=wvij(t)+c1r1[xpij(t)-xij(t)]+c2r2[xgi(t)-xij(t)]

(9)

xij(t+1)=xij(t)+vij(t+1)

(10)

其中：w為慣性權重；c1和c2為學習因子；r1和r2為服從均勻分布U(0,1)的隨機數；i=1,2,…,N，j=1,2,…,N，N為粒子規模。

2.3 PSO優化RBF神經網絡

在已知初始輸入范圍的條件下，運用PSO算法優化出最佳的網絡權值w。取代優化參數向量n為個體粒子，PSO算法每次迭代得到的參數值為

nm=wTm=1,2,…,S

(11)

其中S為粒子種群規模。

不確定性誤差為公式(8)，采用不確定項的逼近誤差作為參數選擇的最小目標函數，設計個體適應度函數為

(12)

粒子群算法更新RBF權值的流程圖如圖1所示。

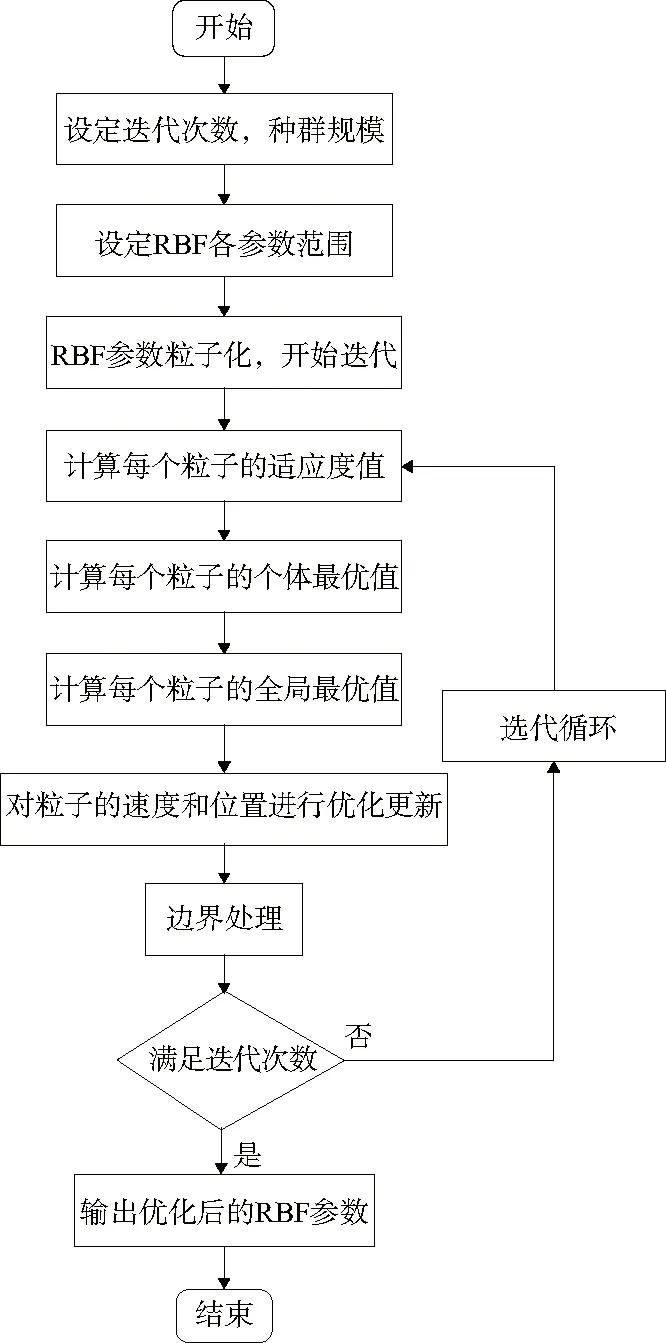
圖1 粒子群優化算法流程圖

3 控制器的設計

在設計好PSO優化RBF參數的流程圖后，PSO-RBF神經網絡自適應控制系統如圖2所示。

圖2 PSO-RBF神經網絡自適應控制系統框圖

根據制定好的PSO-RBF神經網絡自適應控制系統和參考文獻[13]，針對式(1)設計如下控制器：

(13)

將式(13)代入式(1)，整理可得

(14)

(15)

這是一個標準的現代控制理論方程。

設計Lyapunov函數來驗證其穩定性：

(16)

其中γ>0。

對V求導，整理可得

(17)

為了和文獻[13]中的結果進行比較，運用文獻中的自適應率

(18)

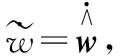
(19)

由上述的已知條件可得

(20)

其中λmin和λmax分別是矩陣Q的最小特征值和矩陣P的最大特征值。

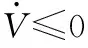
(21)

由式(21)可得出結論，增大Q的特征值或減小P的特征值可以提高x的收斂效果。

4 仿真實驗

本控制是在RBF神經網絡控制的基礎上，通過粒子群算法優化了控制效果，引入文獻[13]中的二連桿機械臂作為被控對象進行仿真對比。

被控對象為雙關節機械臂如圖3所示，其動力學方程為

各項參數參考文獻[13]。

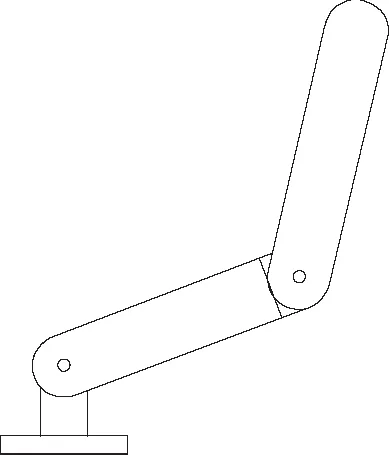
圖3 雙關節機械臂示意圖

設關節角度和關節角速度的期望跟蹤指令為

仿真中，采用控制律式(14)和自適應律式(18)，控制參數取

采用粒子群優化算法對RBF神經網絡中的權值w進行優化，在優化工程中，粒子群優化算法的參數為：迭代次數T=100,種群規模S=50，粒子維數D=10。學習因子c1=c2=0.5。

仿真結果如圖4-圖7所示。

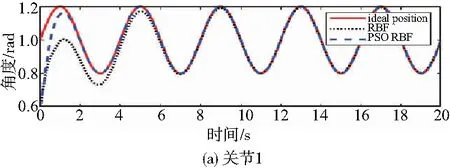
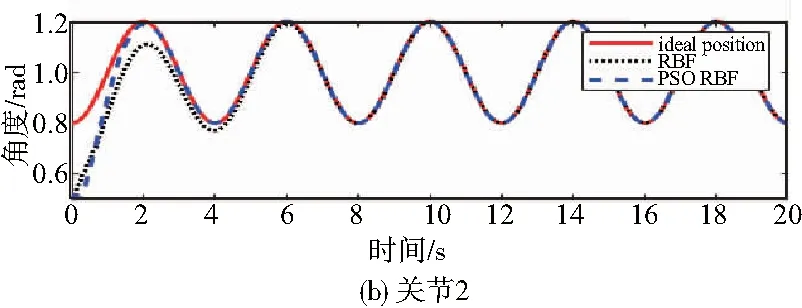
圖4 關節1和關節2的軌跡跟蹤

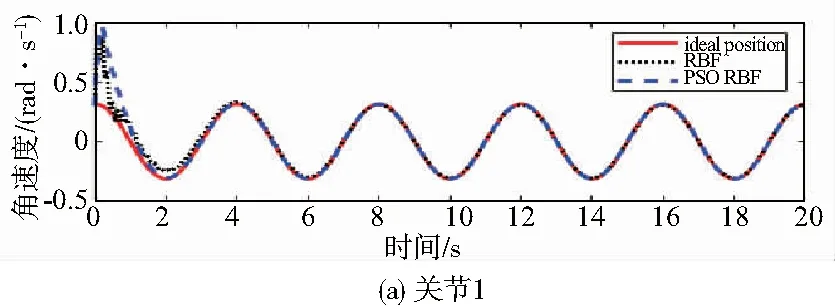
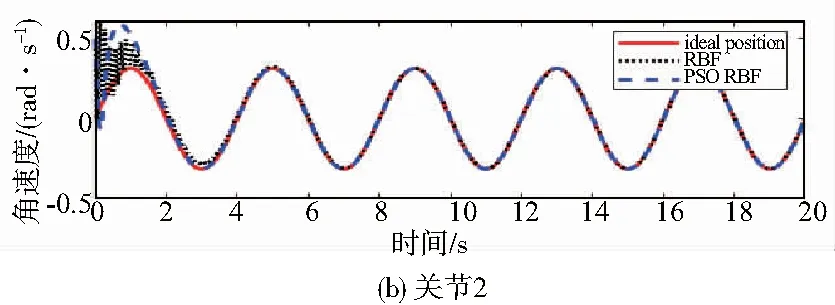
圖5 關節1和關節2的角速度跟蹤

圖6 關節1和關節2的軌跡跟蹤誤差

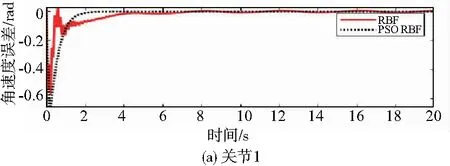
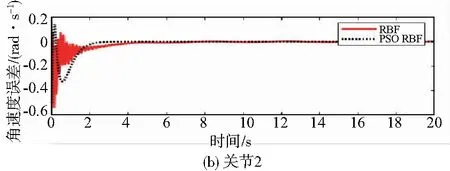
圖7 關節1和關節2的速度跟蹤誤差

從圖4和圖5分析得出，PSO- RBF神經網絡控制的軌跡和速度與理想的軌跡和速度基本吻合，而且與RBF神經網絡控制相比，PSO-RBF的軌跡更快地吻合理想軌跡。

從圖6和圖7可以看出，關節1軌跡吻合快將近4s，關節2軌跡吻合快將近2s。這表明PSO-RBF神經網絡自適應控制實現了二連桿機械臂的高精度軌跡控制效果。通過和RBF控制方法對比，PSO-RBF神經網絡自適應控制方法能夠確保關節1和關節2的不確定項誤差在一個更小的收斂領域，這說明該方法能更快逼近系統不確定項，保證控制系統在更短時間獲得補償并提高性能。

5 結語

1)RBF神經網絡控制能夠在部分未確定機械臂模型參數的情況下獲得較好的軌跡跟蹤性能。而用PSO優化后的RBF神經網絡控制可以獲得更好的軌跡跟蹤性能。

2)通過和RBF神經網絡自適應控制相比，PSO-RBF神經網絡自適應控制系統能夠在更短時間內吻合理想控制軌跡，且控制穩定，提高了控制性能。