基于并聯RSO優化自抗擾的PMSM速度控制

付文強，趙東標，劉凱，趙世超

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引言

永磁同步電機結構簡單，功率密度高，已被廣泛應用于各個領域[1]。由于其是一個強耦合、多變量的復雜系統，使用傳統的PI控制很難提高其調速性能。隨著控制理論的發展，越來越多的非線性控制方法被提出，如魯棒控制[2]、滑模控制[3]、無源控制[4]、自抗擾控制[5](ADRC)等。

ADRC結合了現代控制理論和經典PID控制的優點。ADRC主要由跟蹤微分器，誤差反饋控制律和擴張狀態觀測器組成[6]。擴張狀態觀測器是ADRC的核心，其可以對擾動進行觀測[7]。控制器通過對觀測的擾動進行補償將控制對象轉化為積分串聯型系統[8]。但是，狀態觀測器的觀測精度容易受到擾動量的大小和帶寬的影響。文獻[9]提出了一種最小二乘支持向量機優化ADRC的方法，取得了良好的控制效果。

為了提高PMSM調速系統的速度精度和魯棒性，本文提出了一種基于并聯降階狀態觀測器優化線性自抗擾控制(LADRC)的方法，不僅保留了線性自抗擾參數易整定的優點，還提升了控制器的抗擾動能力，增強了系統的魯棒性。仿真結果表明，該方法能夠提高系統的速度精度和抗干擾能力。

1 永磁同步電機數學模型

對于PMSM的研究，常有以下假設[10]：1)忽略磁路飽和效應；2)忽略磁滯和渦流損耗；3)磁場空間呈正弦分布。在d-q軸系下得到如下表達式：

(1)

式中：id、iq為定子繞組在同步旋轉坐標系下的電流分量；ud、uq為定子繞組在同步旋轉坐標系下的電壓分量；Rs、Lq、Ld分別為定子的電阻和電感；ωm為轉子的機械角速度；Ψr為轉子永磁磁鏈；np為極對數；J、B分別為轉動慣量和阻尼系數；TL為負載轉矩。

對于隱極式PMSM，d軸和q軸的繞組電感相等，代入式(1)，可以得出其運動方程如下：

(2)

式中J∑為等效轉動慣量。

2 傳統線性ADRC速度控制

對于式(2)，將電機的運動方程簡化為

(3)

式中：u=iq；a(t)=-(TL+Bωm)/J∑；b=1.5npΨr/J∑；a(t)視為系統的總擾動。

針對式(3)所示系統，跟蹤微分器可以用一階慣性環節代替，其表達式如式(4)所示。

(4)

式中：v1為跟蹤的輸入信號；r1為跟蹤因子。

該控制器線性擴張狀態觀測器的數學模型為

(5)

式中：z1為ωm的跟蹤值；z2為擾動的觀測值；β01、β02為增益系數。

經過對擾動的補償可以將系統轉換成一個積分環節，采用比例控制律就可以實現很好的控制。針對式(3)所示系統的反饋控制律表達式如下：

(6)

式中k1為比例調節因子，和系統的帶寬有關。

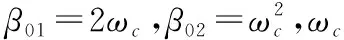
圖1 速度環線性自抗擾控制器結構

3 并聯降階狀態觀測器速度控制

3.1 降階狀態觀測器設計

式(5)中，線性狀態觀測器不僅觀測了擾動值，還對速度ωm進行了觀測。實際上反饋的速度信號可以利用傳感器檢測，觀測的速度可能受到噪聲以及觀測器帶寬的影響。因此，可對上述擴張狀態觀測器進行降階處理。

首先建立式(3)所示系統的狀態方程，設x1為ωm的狀態變量，x2為a(t)的狀態變量，得到其狀態方程如下：

(7)

由于x1已知，x2未知，構建出如下降階觀測器：

(8)

式中β03為觀測器的帶寬。

(9)

式(9)中含有x1的微分項，微分項的引入往往對噪聲特別敏感，為此采用間接的方法對上式進行變換。定義一個新的狀態變量x3=x2-β03x1，定義其狀態估計值為z3，將式(9)簡化得到：

(10)

式(10)完成對系統擾動a(t)的估計，且不含速度的微分項，不會放大噪聲，具有更好的適應性。所得到降階狀態觀測器的結構如圖2所示。

圖2 降階狀態觀測器結構圖

反饋控制率仍采用線性比例控制：

(11)

式中k2為比例系數，和系統帶寬有關。

定義誤差e4=x2-z2，由式(7)和式(9)可得降階狀態觀測器的誤差狀態方程如下：

(12)

式(12)的特征方程為det(s)=s+β03。因此，只要β03>0，同時擾動項a(t)有界，那么降階狀態觀測器就是穩定的[11]。

3.2 速度控制器設計

當擾動幅值較大時，會存在一定的觀測器誤差[12]。假設系統總的擾動a(t)中存在觀測器誤差f′，則有

a(t)=z2+f′

(13)

為了消除觀測器誤差帶來的影響，在原控制系統中并聯一個RSO，用于對誤差f′進行觀測。

因為金錢制度的結果，弄得人類境遇不濟，又因為須傳種的緣故，不得不有家族制，又漸漸的進到國家制度，作為保障，這種無謂的保障，不但無益，還是有害。家族底制度，統是首領制，或包頭制；這種制度，名為擁護人類，其實統以經濟的眼光，去對待人類罷了。家人因為家主是養活我們的，便予以無上的威權；家主因為家人是他養活的，所以就看輕他。家主既有無上的威權，當然就要負保養家人完全的責任；家人也就自卑自棄的墮落他的本能，作非人生的事；如子弟不事生產，家居作樂，于是濫事消費，繁滋生殖，不但弱小人種，還要墮落本能，代代相傳，哪有不窮？這是最明確的證據，余的還有，也說不完。

由式(3)和式(11)可知，系統通過補償得到理想的積分型系統，若觀測器存在誤差f′，則有

(14)

(15)

式(15)和式(7)相似，只是式(15)觀測的是系統與理想積分型之間的誤差，實現對觀測器誤差進行實時的觀測。根據以上對降階觀測器的設計，得到對f′觀測的降階狀態觀測器方程如下：

(16)

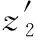
(17)

式(17)完成了對f′估計，對此，反饋控制律的設計也做出相應的修改：

(18)

將式(18)所示控制律代入式(3)就得到了更為精確的純積分系統。為了減少反饋速度噪聲對觀測器的干擾，將反饋信號也增加一個跟蹤微分器，不僅能夠對噪聲進行濾波處理，還能消除反饋信號與輸入信號因跟蹤微分器所帶來的相位滯后。所設計的速度控制器需要整定的參數為：r1、β03、β04、k2，其中β03=β04，為降階狀態觀測器的帶寬。該速度控制器結構如圖3所示。

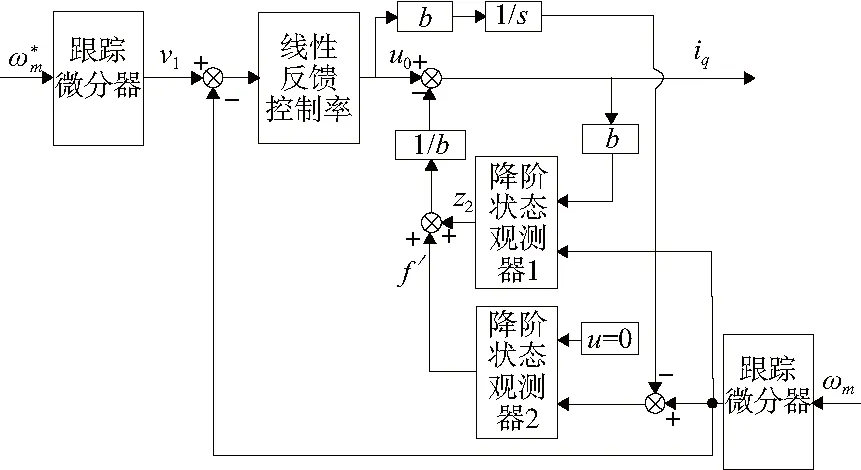
圖3 并聯降階狀態觀測器速度自抗擾控制器結構

根據以上設計，電流環采用PI前饋解耦控制。可以得到本文設計的速度控制結構如圖4所示。

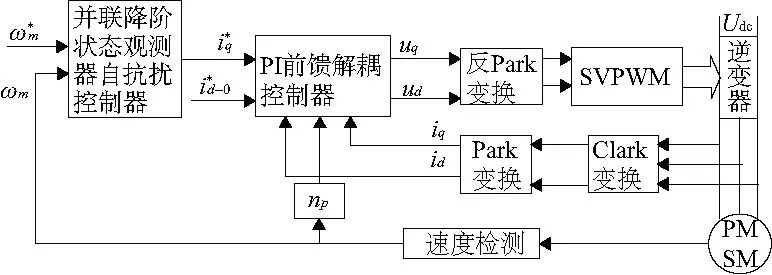
圖4 PMSM速度控制系統框圖

4 仿真試驗

為了驗證所設計控制策略的有效性，在Matlab/Simulink中分別搭建如圖4所示的本文所設計的控制系統、傳統PI控制的調速系統以及傳統線性ADRC調速系統，進行仿真對比研究。本文研究的對象是飛機應急電源地面模擬試驗臺的驅動電機，該驅動電機的具體參數如表1所示。

表1 電機參數

1)速度跟蹤仿真試驗

該仿真試驗策略如下：在電機空載的情況下，設定初始參考速度為3 000r/min；在1s時將參考轉速設定為6 000r/min；在2s時，將參考速度突降為4 000r/min；在3s時，將參考轉速下降為1 000r/min。得到仿真結果如圖5所示。對比圖5(a)與圖5(b)可知，采用PI控制時，速度跟蹤存在一定的超調，超調量最大可達2%；而采用線性ADRC或是本文設計的控制算法，可以實現無超調跟蹤。結合圖5(a)和圖5(b)的穩態速度放大圖可以看出，本文設計的控制算法和傳統線性ADRC控制算法穩態速度精度都比PI控制要高。在低速時，如圖5(b)中1 000r/min，本文控制算法具有更小的穩態誤差。

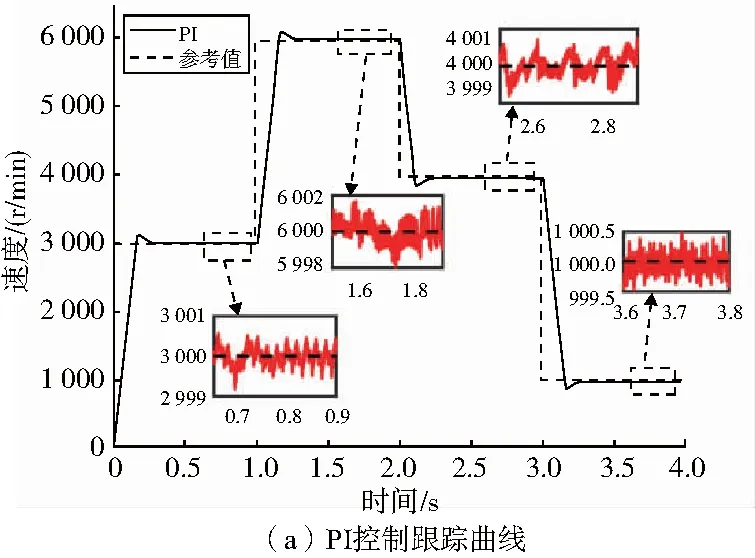
圖5 速度跟蹤曲線

2)負載突變仿真試驗

為了驗證控制策略在負載突變時的適應性，設計如下仿真試驗：電機空載啟動，設定穩態轉速為6 000r/min；當電機達到穩態轉速后，在1s時突加160N·m的負載轉矩；轉速達到穩定之后，在2s時，將載荷卸去，得到系統的速度響應曲線如圖6所示。表2和表3為速度超調量和穩態誤差的計算值。

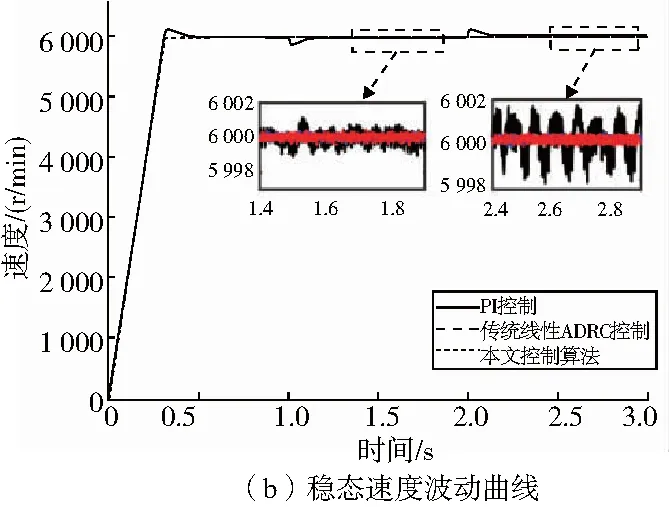
圖6 突加突卸160N·m負載時速度響應曲線

表2 速度超調量 單位：%

表3 穩態速度精度 單位：%

由圖6(a)可知，采用傳統PI控制，無論是加速到穩定轉速，還是突加突卸載荷時，速度超調量都特別大。表2顯示，PI控制的超調量最大達到2.1%。而ADRC控制在轉速上升的時候幾乎沒有超調，但是相比較之下，傳統線性ADRC在負載突變時超調量明顯大于本文所設計的控制策略，傳統線性ADRC在負載突變時速度超調量達到了1.06%，本文控制策略速度超調量僅為0.57%。這是因為負載突變產生的擾動較大，對于傳統線性ADRC，其觀測器受到帶寬的限制，容易受到擾動幅值的影響；而本文設計的速度控制器采用兩個降階的觀測器，在保證帶寬的情況下還可以觀測出觀測器的誤差，能夠提高控制系統的抗干擾能力。同時，可以看出在負載擾動產生之后，PI控制器回復時間最長，其次是線性ADRC控制器，然后是本文設計的控制器，說明本文設計的控制器能夠加快系統受到擾動之后的回復速度。圖6(b)反映的是在負載突變達到穩定之后速度穩態精度，可以看到，PI控制的穩態誤差最大，可達 0.033%。傳統線性ADRC和本文設計的控制策略穩態速度波動都相對較小。

5 結語

線性ADRC控制器可以不依賴于準確的數學模型，對系統的擾動進行觀測和補償。但是線性狀態觀測器容易受到帶寬的限制，影響系統的抗擾動性能。采用并聯降階狀態觀測器的方法，不僅保留了線性狀態觀測器參數易整定的優點，同時還提高了系統的魯棒性。仿真結果表明：

1)采用并聯降階狀態觀測器能夠提高系統的穩態速度精度；

2)使用本文提出的控制算法，系統具有更強的魯棒性，受到擾動之后，能夠更快達到穩定。