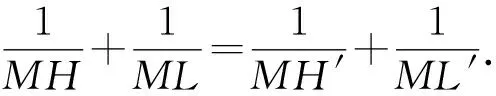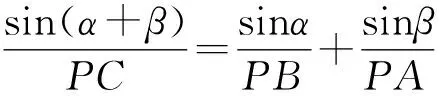張角公式與線段倒數和差關系的證明
于志洪
(江蘇省泰州市海陵區森南新村15棟103室 225300)
1 引例

證明因為S△PAB=S△PAC+S△PCB,
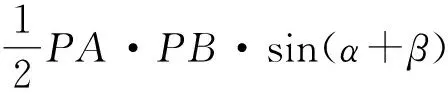
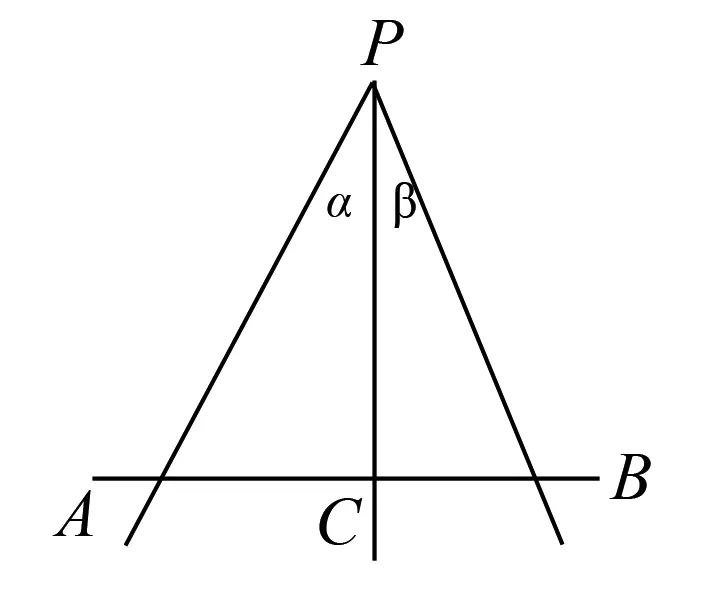
圖1
例1 如圖2,已知圓心O在Rt△ABC的斜邊BC上,且與AB,AC相切,設圓的半徑為r.
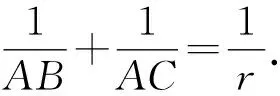
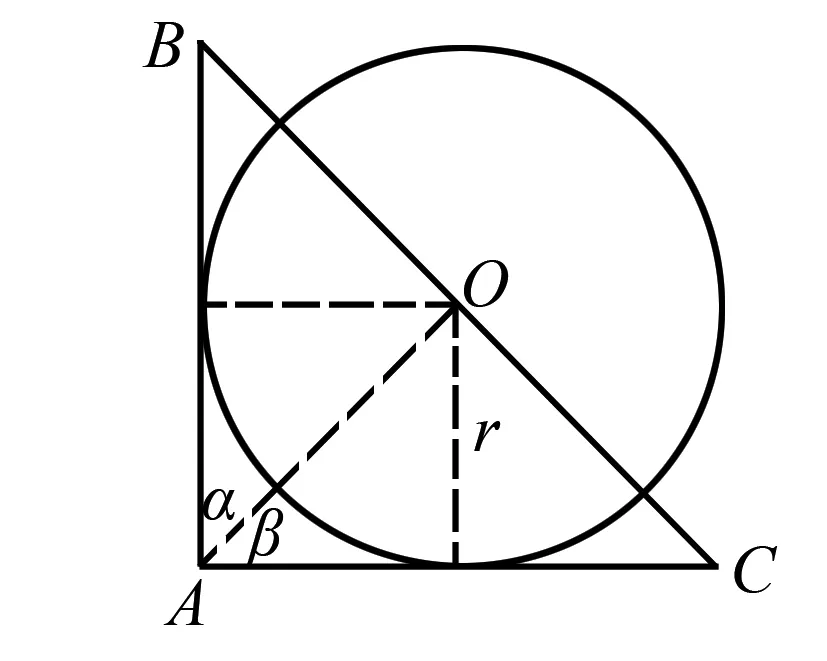
圖2
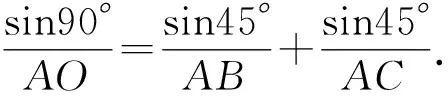
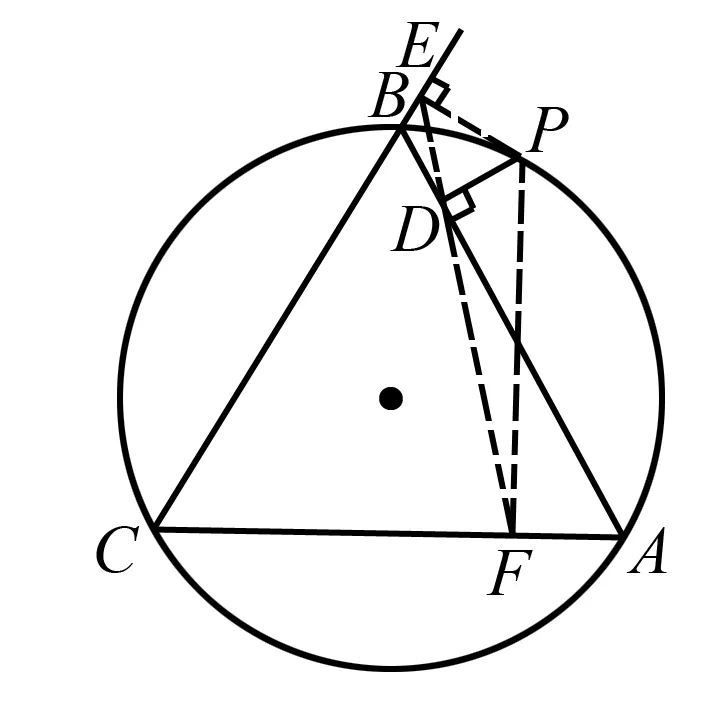
圖3
證明過點P作PD⊥直線AB于點D,作PE⊥直線BC于點E,作PF⊥直線CA于點F.
知P,E,B,D及P,D,F,A分別四點共圓及PD=d1,PE=d2,PF=d3.
則∠DPE=∠ABC=60°,∠DPF=∠CAB=60°.
由西姆松定理,知D,E,F三點共線.
從而以P為視點,對△PEF應用張角公式,有
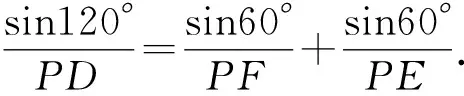
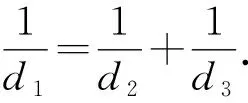
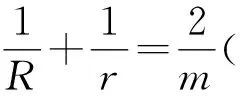
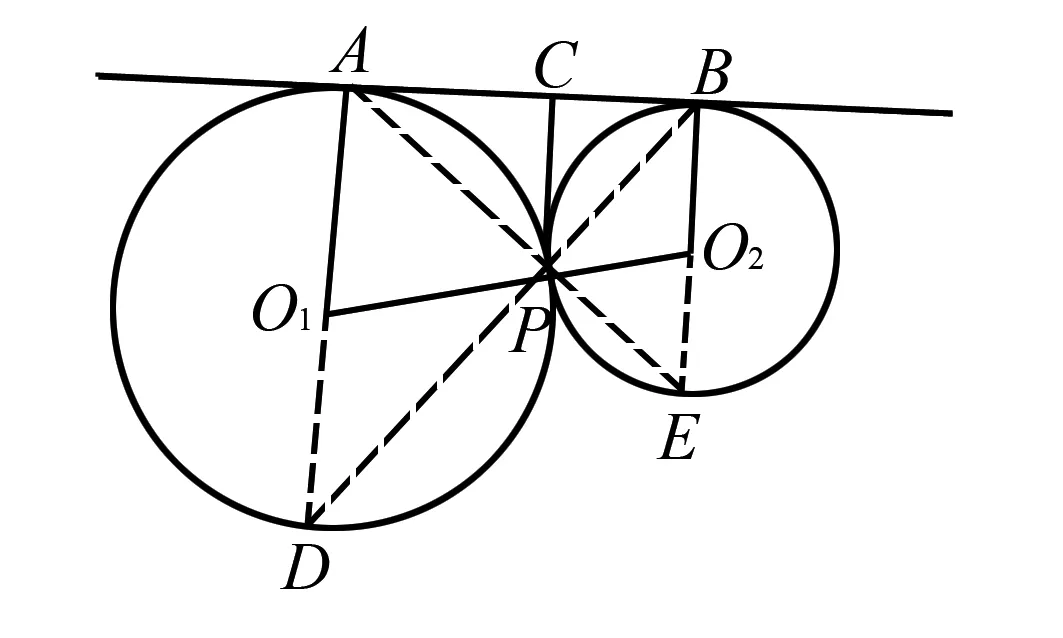
圖4
證明作兩圓的直徑AO1D和BO2E,連接PA,PB,PD,PE.容易證明A,P,E和B,P,D分別共線.設∠APC=∠E=α,∠BPC=∠D=β,在Rt△APD和Rt△BPE中,分別得
PA=2Rsinβ,PB=2rsinα.
①
②
例4 如圖5,在凸四邊形ABCD中,對角線AC與BD互相垂直,過AC,BD的交點O任作兩直線分別交AC,BC,AB,CD于點E,F,G,H.又GF,EH分別交BD于點I,J.
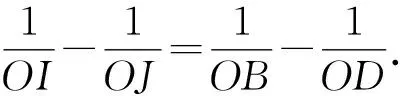
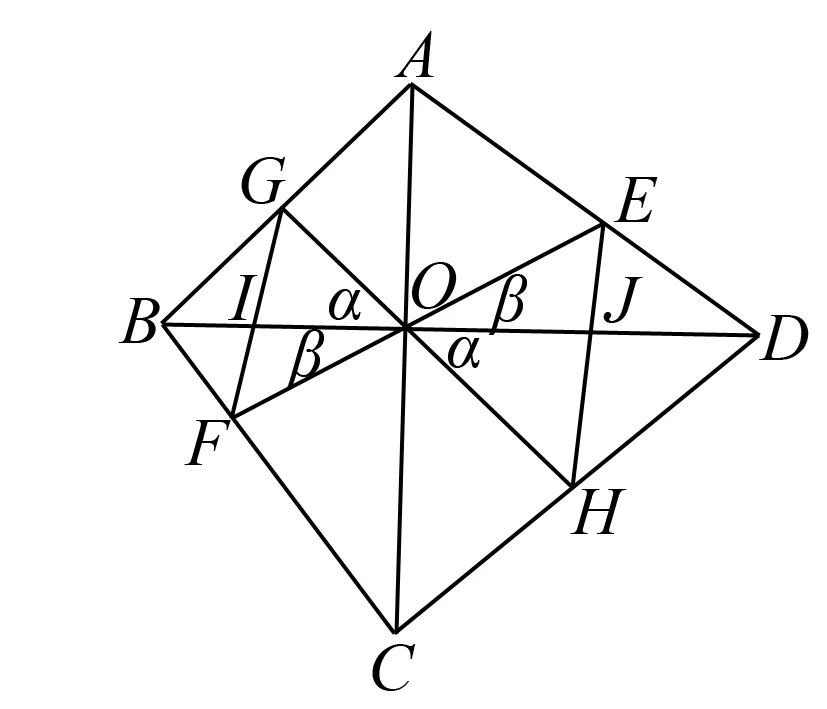
圖5
證明設∠GOI=∠JOH=α,∠FOI=∠EOJ=β,由題設易知∠AOG=∠COH=90°-α,∠COF=∠AOE=90°-β.
所以以O為視點,對A,G,B用張角公式,得
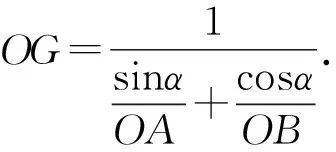
③
同理以O為視點,對B,F,C用張角公式,得
④
又以O為視點,對G,I,F用張角公式,得
⑤
將③和④同時代入⑤中,得
⑥
同理可得
⑦
所以⑥-⑦,得
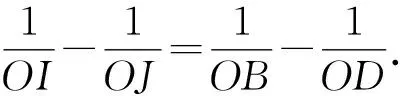
例5 如圖6,在直線l的同側有相鄰的三個等角∠BAD,∠DAN和∠NAG,且G,A,B都在l上,連接GD,BN分別交于AN,AD于N,L.
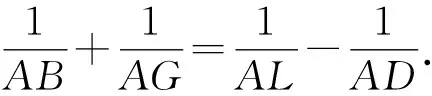
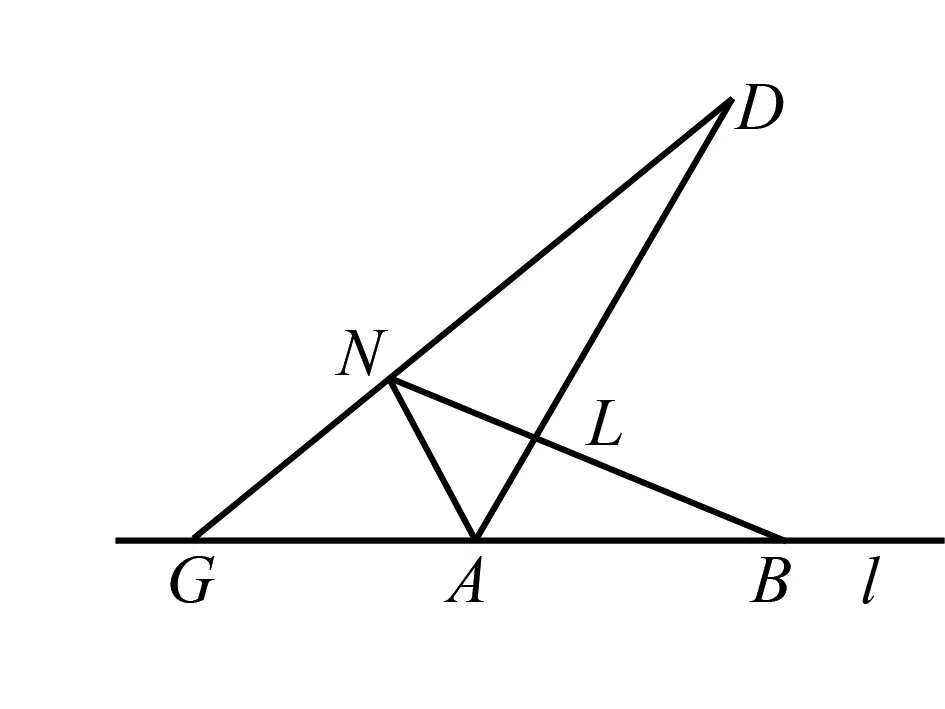
圖6
證明以A視點,分別對B,L,N及G,N,D用張角公式,得
⑧
⑨
又sin60°=sin120°,
例6凸四邊形ABCD的一組對邊BA與CD的延長線交于點M,且AD∥BC,過點M作截線交另一組對邊所在直線于H,L,交對角線所在直線于H′,L′.
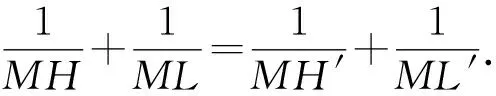
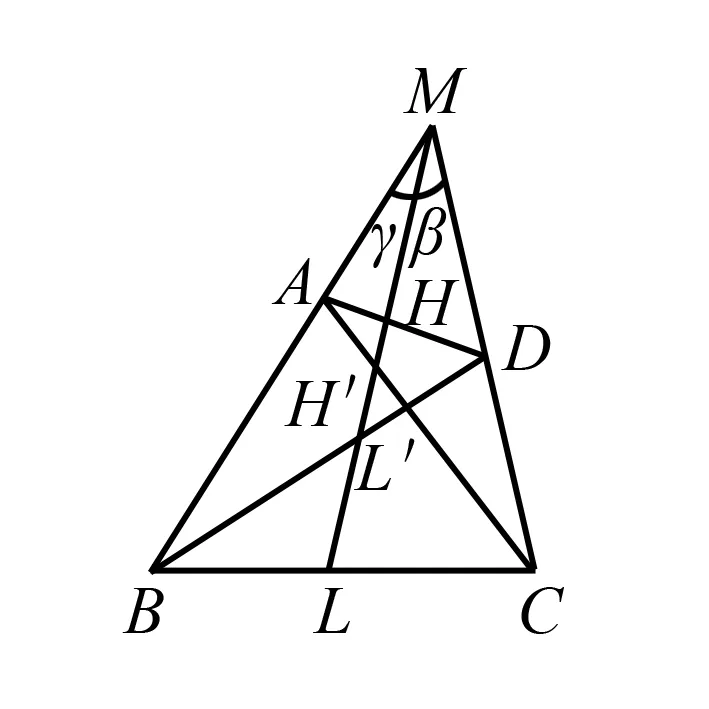
圖7
證明如圖7所示,設∠BML=γ,∠CML=β,應用張角公式得
⑩