近五年全國卷Ⅰ物理選修3-5模塊命題特點及教學啟示

陳洪軍

(江蘇省鎮江心湖高級中學 212132)

高中物理選修三系列教材中，3-5模塊主要研究動量守恒、原子原子核及波粒二象性等內容，在全國高考中的考查經歷了由2016年及之前的選考發展到今天的必考，而且有與其他物理規律綜合交叉考查的發展趨勢，彰顯出國家層面對育理工人才、選拔科技人才的新的理念，因此，對高考試題中3-5模塊試題的分析研究顯得尤為必要，這里針對全國卷I近五年3-5部分的試題作一粗淺統計分析.

1 近五年全國卷Ⅰ 3-5模塊內容考查統計

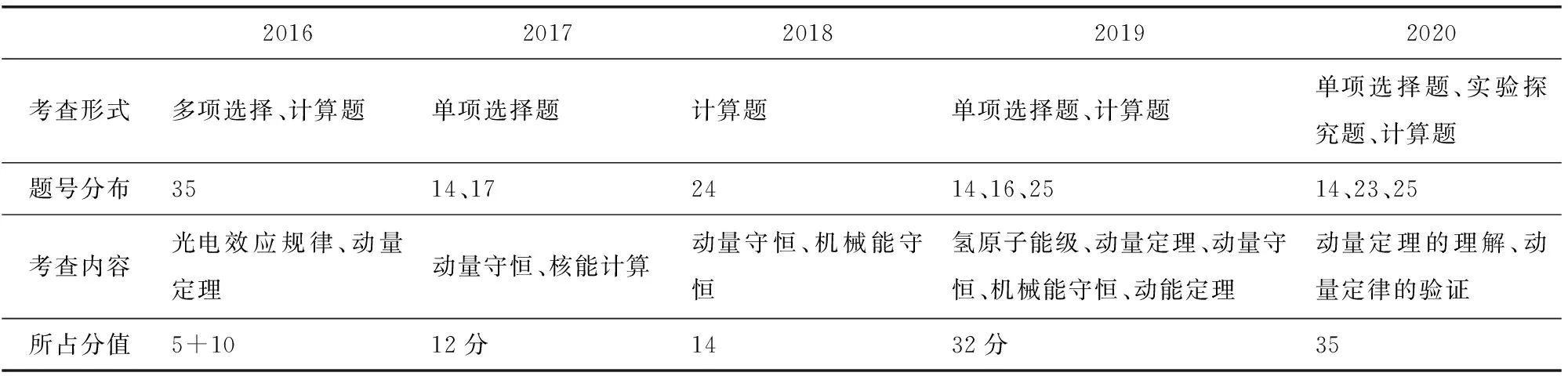
表1 近五年全國卷Ⅰ 3-5模塊內容考查統計

由表中對近五年全國卷Ⅰ 3-5部分的考查統計不難發現以下規律：

(1)試題形式上看，3-5部分的考查囊括了填空、單項選擇、多項選擇及計算等幾乎所有形式的物理題型，且近年來越來越趨向于以計算題形式呈現;

(2)題號上看，因2016及以前是選考題形式考查，2017及以后以必考題形式考查，故2016固定在第35題，而隨后的2017、2018、2019、2020在試卷中呈現的次序則從14至25不等，題號靈活多樣，不拘泥于35題一種題號;

(3)從試題數目上看，近五年呈現出由2016的固定為全卷第35一道題發展至2017年的兩道題，再縮減至2018年的一道計算題，最后上升至2019和2020年的三道題，可謂一波三折，有增有減；

(4)從設問數目來看，計算題均為多個小問形式呈現，目的是增強考查面，使知識點盡可能多的覆蓋到;

(5)從考查內容上看，以動量定理、動量守恒為高頻考點，其余如光電效應、氫原子能級、核能等時有考查，且動量守恒的考查由過去的單獨命題考查，發展至與機械能守恒、動能定理等必修系列內容的綜合滲透考查；

(6)分值上看，3-5模塊在高考中的分值占比由16年的15分降至17年的12分，再回升至2018年的14分，而2019年卻高達32分之多，2020年最多為35分，顯然，全國卷Ⅰ對3-5模塊的考查變得越發重視，試題綜合性程度變強、所涉物理定律、定理變多，所占分值也隨之變大.

2 典型試題剖析

2.1 光電效應的考查

例1(2016全國卷Ⅰ)現用一光電管進行光電效應的實驗，當用某一頻率的光入射時，有光電流產生.下列說法正確的是____.

A．保持入射光的頻率不變，入射光的光強變大，飽和光電流變大

B．入射光的頻率變高，飽和光電流變大

C．入射光的頻率變高，光電子的最大初動能變大

D．保持入射光的光強不變，不斷減小入射光的頻率，始終有光電流產生

E．遏止電壓的大小與入射光的頻率有關，與入射光的光強無關

命題意圖本例以多項選擇的形式考查學生對光電效應發生條件、光電子最大初動能和飽和光電流的影響因素及遏止電壓等光電效應規律的理解.

試題解析答案：ACE

2.2 氫原子能級的考查

例2 (2019全國卷Ⅰ)氫原子能級示意圖如圖1所示.光子能量在1.63 eV～3.10 eV的光為可見光.要使處于基態(n=1)的氫原子被激發后可輻射出可見光光子，最少應給氫原子提供的能量為( ).

A．12.09 eV B．10.20 eV

C．1.89 eV D．1.5l eV

命題意圖試題給出氫原子能級圖及可見光光子能量范圍，考查學生對原子躍遷條件、原子發光頻率條件等玻爾假設的理解.

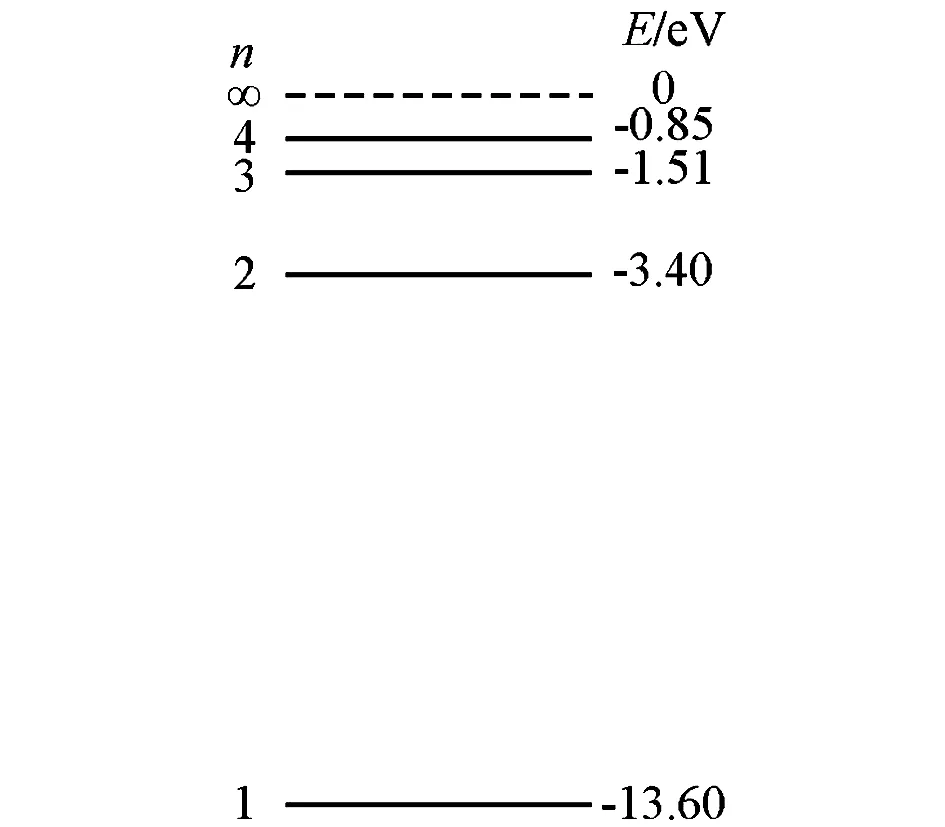
圖1

試題解析處于基態的氫原子其能量為-13.6eV，當其躍遷到量子數為2的能量狀態時，至少要向其提供-3.40eV-(-13.6eV)=12.09eV能量，而后其可向基態躍遷，輻射出可見光光子.

2.3 核能計算的考查

A．3.7MeV B．3.3MeV

C．2.7MeV D．0.93MeV

命題意圖試題給出了核聚變的經典核反應方程式，要求學生計算所釋放的核能，旨在考查學生運用質量虧損法計算核能的能力.

試題解析核能為△E=3.2585MeV≈3.3MeV,選項B正確.

2.4 動量定理的考查

例4(2016全國卷Ⅰ)某游樂園入口旁有一噴泉，噴出的水柱將一質量為M的卡通玩具穩定地懸停在空中.為計算方便起見，假設水柱從橫截面積為S的噴口持續以速度v0豎直向上噴出；玩具底部為平板(面積略大于S)；水柱沖擊到玩具底板后，在豎直方向水的速度變為零，在水平方向朝四周均勻散開.忽略空氣阻力.已知水的密度為ρ，重力加速度大小為g.求:(1)噴泉單位時間內噴出的水的質量；(2)玩具在空中懸停時，其底面相對于噴口的高度.

命題意圖知識角度，試題考查動量定理、物體平衡、勻變速直線運動、牛頓運動定律等核心知識；能力角度，試題以生活中常見的噴泉為命題背景，考查了學生將具體情境轉化為物理問題的模型構建能力、運用核心定律綜合分析推理能力及解決實際問題的能力；核心素養角度，通過對學生的模型建構、演繹推理科學思維素養的考查，旨在對學生通過學習是否形成了正確的相互作用觀、運動觀、物質觀和能量觀等物理觀念.

試題解析(1)設極短時間Δt內噴出的水柱高度為Δh，因所取時間極短，故可看成以速度v0勻速運動，則有：

Δh=v0Δt

①

由密度公式得所形成水柱質量為：

Δm=ρΔV=ρsΔh

②

由①②兩式可得在極短時間內Δt所形成的水柱質量為：

Δm=ρsv0Δt

③

將③式變形整理可得單位時間內噴泉噴出的水的質量為

(2)當玩具穩定在水柱上方時，由二力平衡得水柱對玩具的作用力：

F=Mg

由牛頓第三定律可得玩具對水柱的反作用力為：

F′=F=Mg

④

設在極短時間Δt內水柱到達玩具底部時的速度為v1，豎直方向由動量定理可得：

(F′+Δmg)·Δt=Δmv1

⑤

再由勻變速直線運動規律得：

⑥

因極短時間內水柱質量Δm很小，⑤式左邊可將其忽略為零，則由③、④、⑤三式可得高度

2.5 動量守恒與機械能的滲透考查

例5(2018全國卷Ⅰ改編)一質量為m的煙花彈獲得動能E后，從地面豎直升空，當煙花彈上升的速度為零時，彈中火藥爆炸將煙花彈炸為質量相等的兩部分，兩部分獲得的動能之和也為E，且均沿豎直方向運動.爆炸時間極短，重力加速度大小為g，不計空氣阻力和火藥的質量，求爆炸后煙花彈向上運動的部分距地面的最大高度.

命題意圖試題以學生熟悉的煙花彈的燃爆為背景，將守恒思想(動量守恒、能量守恒)植入其中，考查學生在具體生活情境中運用守恒思想解決實際問題的能力.

試題解析煙花彈自地面升至高為H1過程中根據機械能守恒定律得

mgH1+0=E+0

①

因煙花彈被炸成一上一下兩部分則爆炸前后由動量守恒得

m1v1+m2v2=0

②

又據爆炸前后兩部分動能之后仍為E得

③

由題意知被炸后的兩部分質量相等，均為均為

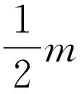
④

爆炸后的上部分自爆炸后瞬間至最高點由機械能守恒定律得

⑤

綜合①②③④⑤式可得，爆炸后煙花彈上部分距地面的最大高度為