核心素養引領下的高中數學課堂教學最優化初探
周小平
(浙江省杭州市新登中學 311404)
數學課堂教學的一個重要部分是例題教學,教師的教學應圍繞核心素養這個主題,充分發揮習題、例題的潛能作用,在教學中引導學生研討一類習題及推廣、引伸,使其問題變寬、變深、變活,從而起到鞏固基礎知識、形成基本技能、完善基本方法、總結基本經驗,達到形成學生核心素養的目的,并從中選出好的題目,好的方法,達到最優化的教學.
1 一題多變,在問題的層層推進中,滲透數學素養
設計問題鏈,在問題的層層推進中,深化問題,把這個例題達到高考的要求,進而使學生“有梯可上,有扶手可抓,步步登高”,形成學生解決這類問題的思維素養,并能使學生始終處于愉快的探索狀態,知識體系得以鞏固提升.為了達到高考對求函數零點的要求,設計了如下問題鏈.

變式1 若g(x)=log2x,判定函數F(x)=f(x)-g(x)的零點有____個.
變式2 若g(x)=log2m,判定函數F(x)=f(x)-g(x)的零點有____個.
變式3 若g(x)=log2x,判斷F(x)=f[g(x)]-1的零點有____個.

(1)y=f[g(x)]-1的零點個數;
(2)方程ag2(x)+bg(x)+2=0有四個根時,實數a,b的關系是什么?
通過這幾個問題鏈, 把零點問題提高到了高考的高度,使學生在這一系列的問題中,思維層層推進,把潛藏的思路、規律、本質發掘出來,數學素養無形中得以形成.
2 一題多法,在問題的多種解答中,提升數學素養
同一事物或現象,當人們站在不同角度來觀看、審視時,就會看到不同景觀,正所謂“橫嶺側峰”.引導學生對同一題目從不同角度快速聯想及思考問題,探求解答的不同方案,從而拓寬思路,培養思維的廣度、深度,進而讓學生選擇適合自己的方法,達到方法最優化.


圖1










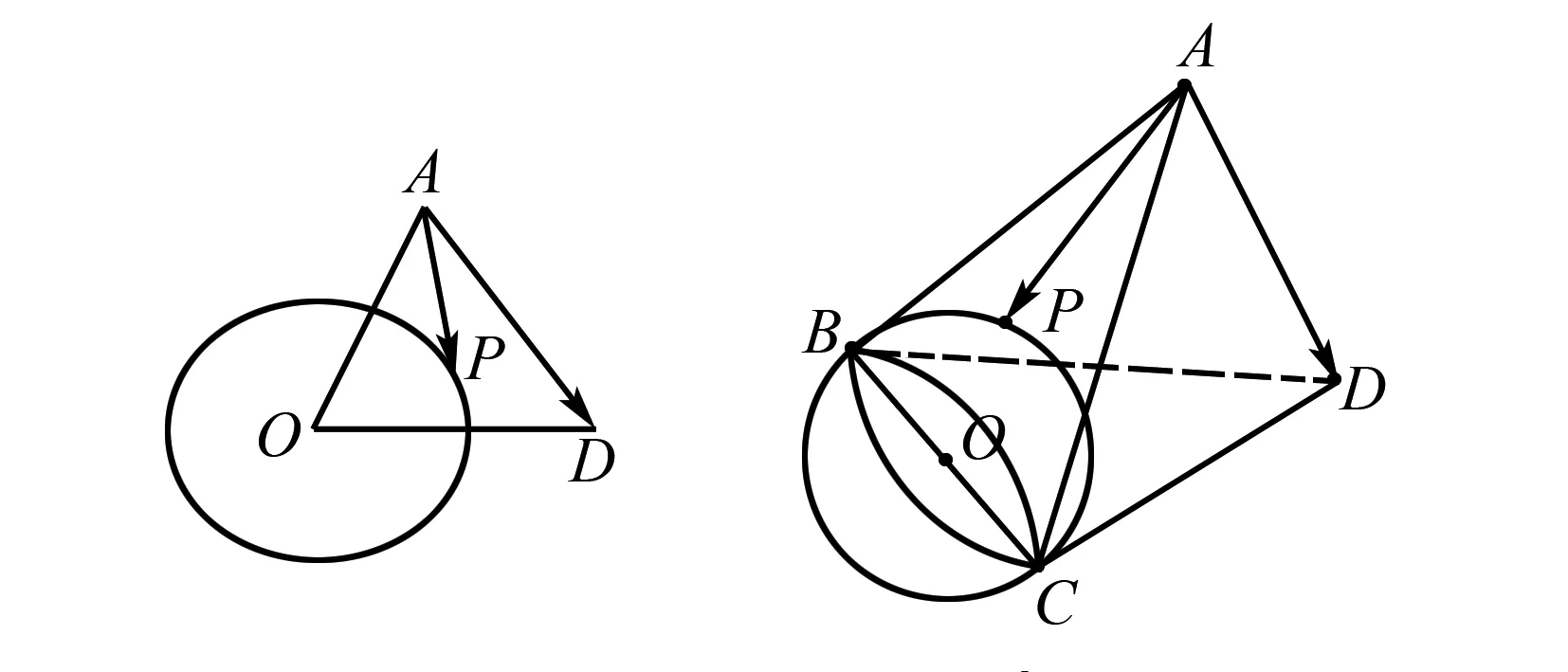
圖2 圖3





圖4
3 一法多題,在多題的類同解法中,拓展數學素養
在高考數學試題中,運用線性規劃思想,妙解函數、不等式、概率、數列、解析幾何等問題.一法通用,一法通關,從而達到熟一法、懂一類的效果,并通過這樣一種方法,尋找各個知識模塊之間的聯系,充分體現了核心素養的特性.
例3(2015年浙江文科高考試題)設函數f(x)=x2+ax+b,(a,b∈R).已知函數f(x)在[-1,1]上存在零點,0≤b-2a≤1,求b的取值范圍.


變式3 已知直線l:2tx+ty+1=0和點A(1,3)和B(5,4),若直線l與線段AB有公共點,求實數t的取值范圍____.
4 引申變式,在問題的創新轉換中,推進數學素養
研究高考問題和課本例題、習題之間的關聯, 通過引申變式,讓學生看到一題通過多次引伸后如何出現在高考試卷上,讓學生真正理解高考試題如何“源于課本,高于課本”.數學思想達到最優的提升,推進數學素養.



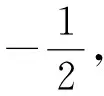
(1)求C的方程,并說明C是什么曲線;
(2)過坐標原點的直線交C于P,Q兩點,點P在第一象限,PE⊥x軸,垂足為點E,連接QE并延長交C于點G,證明:△PQG是直角三角形.
方法小結第(1)問與課本的例題是一樣的,這體現了高考試題源于課本,第(2)問可以根據例題加以引申得出結論,達到高于課本,達到高考的要求.
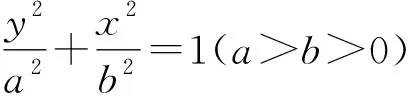
變式2 (2012年湖北理高考)設A是單位圓x2+y2=1上的任意一點,l是過點A與x軸垂直的直線,D是直線l與x軸的交點,點M在直線l上,且滿足|DM|=m|DA|(m>0,且m≠1).當點A在圓上運動時,記點M的軌跡為曲線C.
(1)求曲線C的方程,判斷曲線C為何種圓錐曲線,并求其焦點坐標;
(2)過原點且斜率為k的直線交曲線C于P,Q兩點,其中點P在第一象限,它在y軸上的射影為點N,直線QN交曲線C于另一點H.是否存在m, 使得對任意的k>0, 都有PQ⊥PH? 若存在,求m的值;若不存在,請說明理由.
數學基本知識、基本技能是雙基目標,隨著課程標準的要求,在雙基的基礎上加上數學的思想方法和數學基本活動經驗,這就形成了四基.學生四基的構建和形成,自然而然變成了學生的三維目標,進而形成學生的核心素養.
總之,指點學生往哪里走,比教會學生怎樣走路更重要,因此知識引領、能力引領、思想引領、經驗引領也更加重要.高中數學作為基礎教育課程應體現其基礎性、拓展性、發展性.從期望學生“學會什么”出發,逆向設計“學生何以學會”的過程,作為每一節課的初衷,設計上好每一節課,給每一位學生每一天一份適合的禮物,讓學生有所學、有所會、有所懂、有所用,為學科核心素養的落地指明清晰的路徑.

