直廓環面蝸桿傳動的高次方修形原理

趙亞平，李帥，陳新元，李公法

（1.東北大學機械工程與自動化學院，遼寧沈陽 110819；2.武漢科技大學機械傳動與制造工程湖北省重點實驗室，湖北武漢 430081；3.武漢科技大學冶金裝備與控制技術教育部重點實驗室，湖北武漢 430081）

直廓環面蝸桿副最初由英國的Hindley 于1765年首先發明［1］.1909 年，美國的Cone 進行了重要改進.實際上在此之前，德國的Lorenz博士就制成過這種蝸桿副，并取得了專利權［2］.

與包絡環面蝸桿副相比，直廓環面蝸桿副主要優點為：1）一般不存在邊齒變尖［3］.2）在軸截面內，相應蝸輪環面滾刀的齒廓為直線段［4］，有利于刀具檢驗和測量.但也存在一些不足之處［5］：1）其蝸輪齒面上接觸區面積較小.2）蝸桿螺旋面是不可展的直紋面，難于按成形原理精確磨削.

直廓環面蝸桿傳動有原始型和修正型之分.原始型傳動由于蝸輪齒面上存在所謂的“常接觸線”，容易造成蝸輪的早期失效，多不主張采用［6］.修正型傳動按原理可以歸結為基于實測磨損量的自然修形，和基于嚙合理論的理性修形.其中前者屬于半經驗半解析的修形方法.

自然修形最早由前蘇聯學者提出，通過實測獲得經過一定運轉時間后的蝸桿分度環面上的磨損量曲線，即所謂自然修形曲線［7］.進而采用拋物線對自然修形曲線進行擬合，實現拋物線修形.由于拋物線修形在本質上屬于變工藝傳動比修形，在數控裝置普及之前，在生產實踐中實現，有一定困難，因之曾采用變參數修形予以替代［8］.

為了提高自然修形曲線的擬合精度，80 年代曾有學者提出高次方修形.在自然修形的研究過程中，長期沒有獲得加工修形蝸桿的工藝傳動比的明確計算式，后來得到該計算式后，也沒有在嚙合分析計算的過程中，始終把工藝傳動比當作變量處理，造成嚙合分析的結果不能準確反映蝸桿副的實際工作狀況［9］.作為自然修形的一個變種，曲率修形通過建立修形量微分與蝸桿齒面曲率半徑微分間的關系，修正蝸桿齒厚達到修形目的［10］.

隨著嚙合理論的發展，誕生了理性修形.其基本原理是，在加工蝸桿或相應滾刀的過程中，蝸桿毛坯與刀座的相對位置及相對運動，和蝸桿副嚙合過程中，蝸桿蝸輪的相對位置及相對運動，存在人為設置的差異，實現修形，達到去除常接觸線擴大共軛區的目的.由于上述差異可以人為設置，意味著理性修形中，工藝傳動比可以取常值，從而降低理性修形實現的難度.

理性修形中，可調參數較多，諸如：工藝中心距、工藝傳動比、刀座垂直高度、以及刀座軸線偏轉角度等等，從而形成各色修形傳動.不過，按照嚙合特點，這些修形傳動可以劃分為：Ⅰ型傳動、Ⅱ型傳動和角修形傳動等有限的類型.理論研究表明，綜合施加不同參數修形，才能獲得嚙合性能較為優越的傳動副.

本文基于自然修形數據，對其無量綱化處理后，用高次多項式擬合得到具有普適性的高次修形曲線，推導了修形曲線與工藝傳動比i1d的關系式.根據微分幾何及齒輪嚙合理論系統地建立了具有變工藝傳動比直廓環面蝸桿副的數學模型，證明了蝸桿螺旋面是不可展直紋面.并通過相關算例分析了高次方自然修形直廓環面蝸桿的局部嚙合性能.

1 加工蝸桿工藝傳動比的計算原理

1.1 高次方修形曲線

高次方修形曲線的優劣直接影響到蝸桿副的嚙合性能，既有文獻中的修形曲線是在特定參數下得到的.為擴充修形曲線的適用范圍，進一步提高擬合精度，需建立普適型修形曲線.

在精車蝸桿螺旋面的過程中，蝸桿繞其軸線的轉角為φ，車刀的所謂標稱角度是φx，它們的幾何關系如圖1所示.據此可以把φx表示為

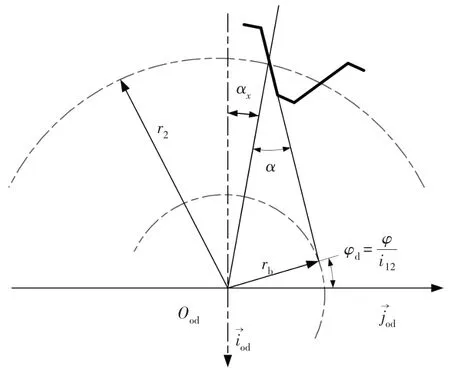
圖1 蝸桿轉角φ與標稱角度φx的關系Fig.1 Relationship between worm angle φ and nominal angle φx

式中，α是蝸桿分度環面壓力角.

文獻［9］中對中心距a=500 mm、傳動比i12=8的蝸桿副，按不同的標稱角度φx，實際測量修形量，共獲得i=35 組數據().建立修形曲線前，先對所得的數據無量綱化處理.為此首先定義轉角系數

式中，φw為蝸桿包圍蝸輪工作半角.

同樣定義修形量系數Ii=，根據文獻［8］，不同中心距、傳動比條件下蝸桿嚙入端修形量Δf/mm可按下式計算

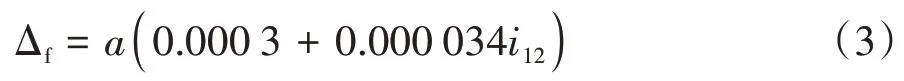
其中，a為蝸桿副標稱中心距；式中10.25≤i12≤59.

文獻［9］中的數據，經上述方法處理后，得到的無量綱化的修形數據列于表1.

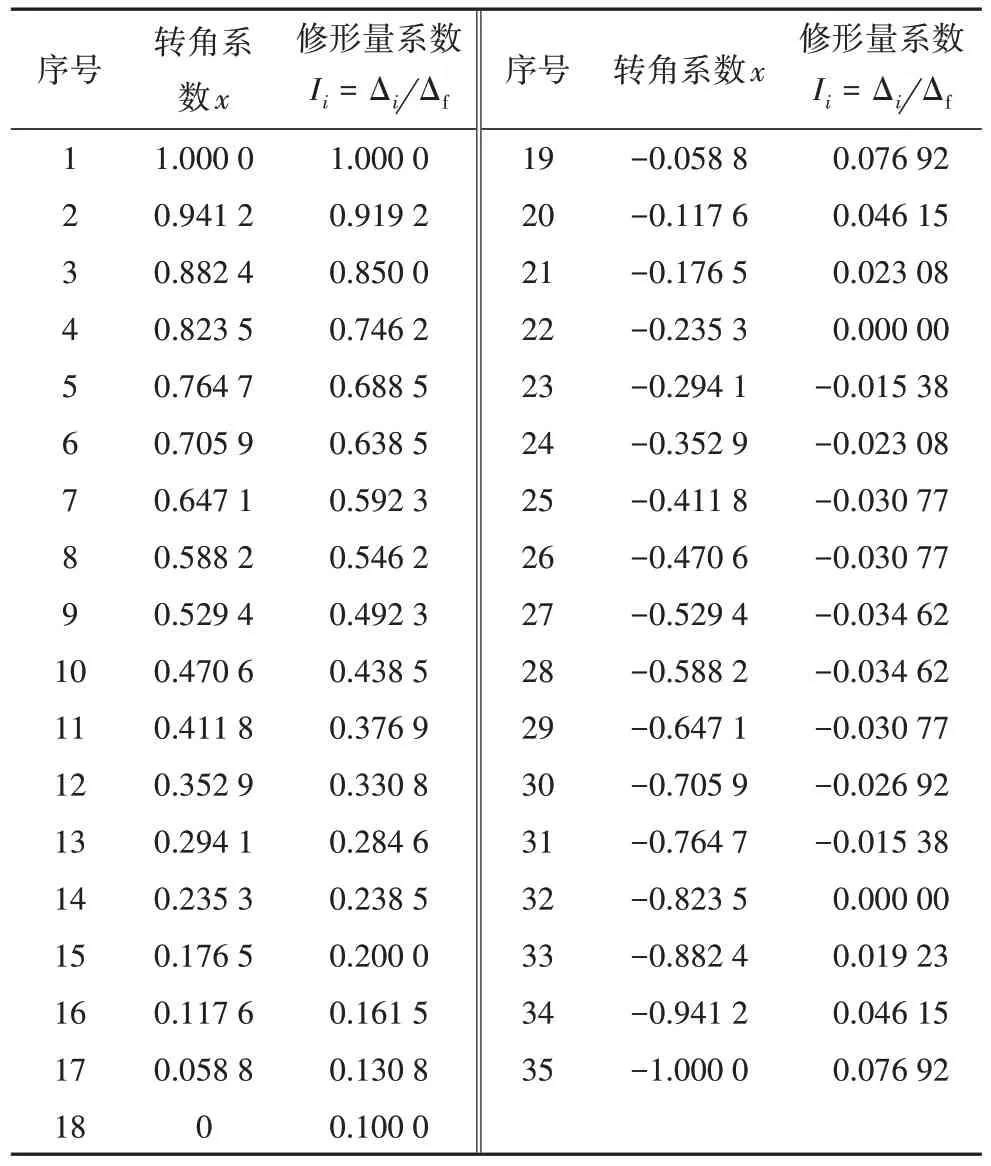
表1 無量綱化修形數據結果Tab.1 The result of dimensionless modification data

對上述修形數據以最小二乘法擬合得到修形量系數的函數為

對式中多項式冪次n取不同數值，可得到式中不同次多項式的系數ck，將計算的數值結果列于表2.

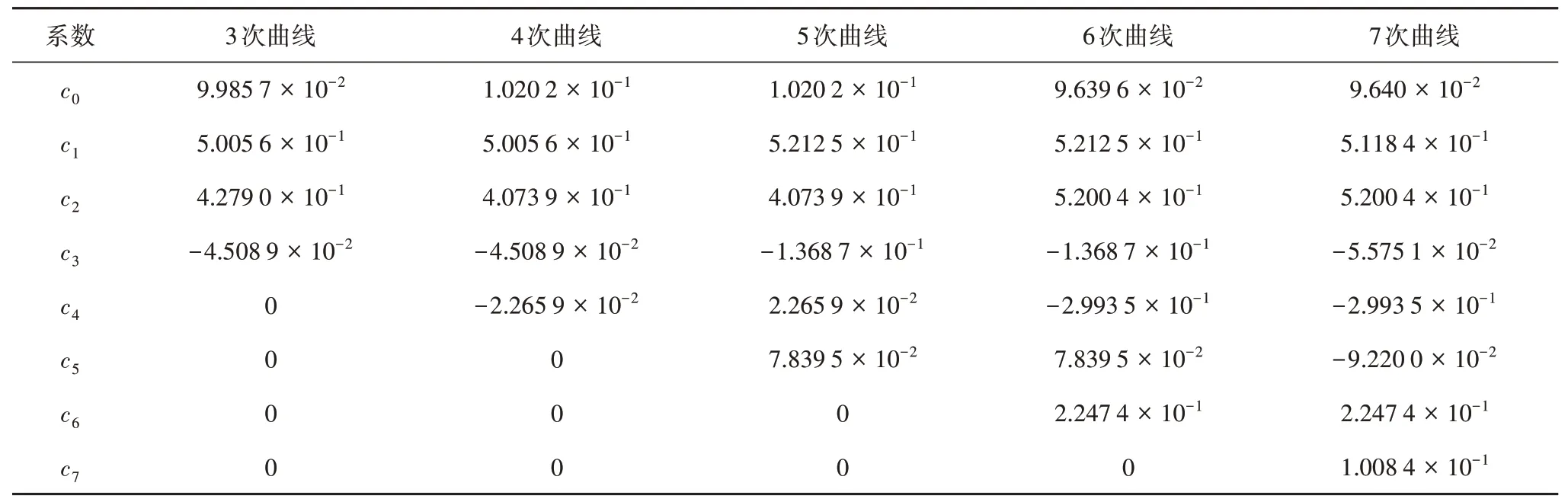
表2 各次修形曲線多項式系數Tab.2 Polynomial coefficients of various modification curves

以3 次修形量系數的函數為例，擬合得到的曲線圖像如圖2.x=-1，x=0，x=1 分別對應蝸桿副的嚙出端、喉部和嚙入端.

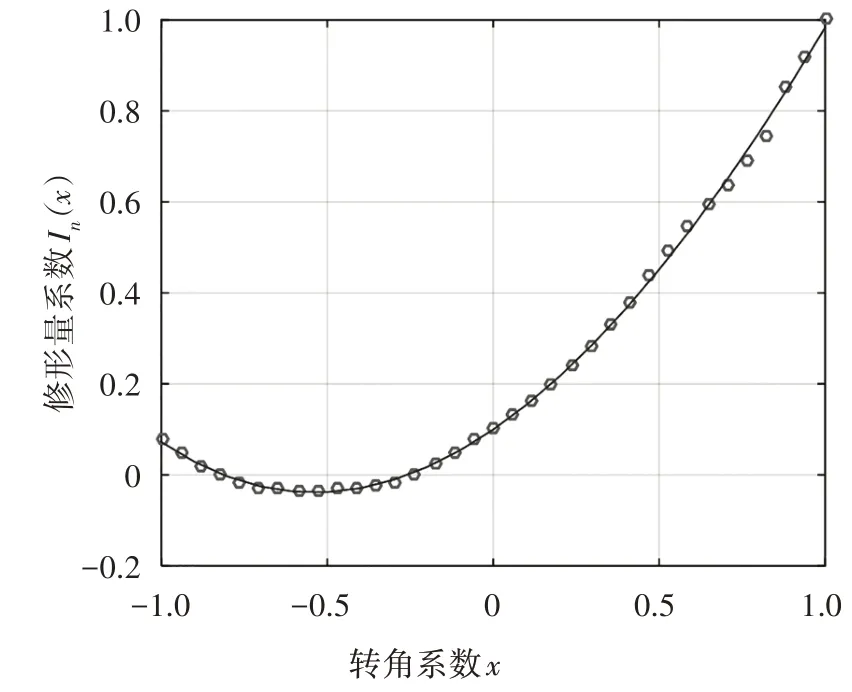
圖2 3次修形量系數的函數曲線Fig.2 The curve of the coefficient of the cubic modification amount

由式（4）和表2 中的數據得到修形曲線函數表達式為

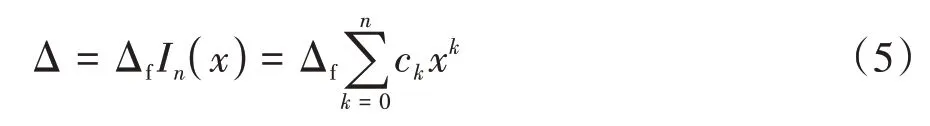
當多項式冪次n=2 時，式（5）為拋物線修形曲線函數；當n＞2，即為高次方修形曲線函數.

通過提高擬合多項式的次數n，可以提升式（4）的擬合精度.為此基于表1 中數據計算各次曲線的誤差，其結果如表3所示.

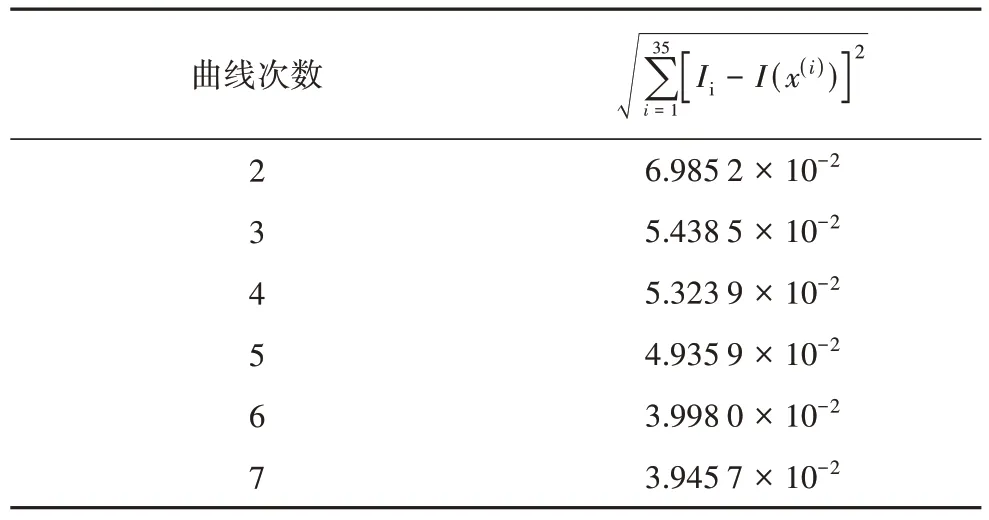
表3 各次曲線的總誤差Tab.3 Total error of various curves

由表3 可知，單純提高擬合多項式的次數，并不能顯著提升擬合精度.

1.2 工藝傳動比與修形曲線函數的關系

由圖1 可建立加工蝸桿毛坯時刀具的附加轉動Δφd與修形量變化的關系式

式中，r2為蝸輪分度圓環半徑.

因此，加工修正型直廓環面蝸桿時刀具轉角為

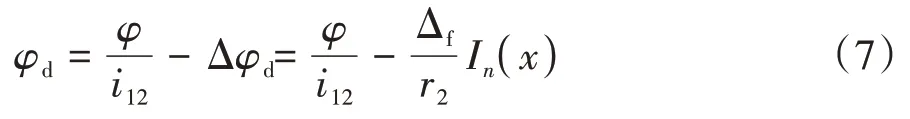
任意轉角下刀座與蝸桿的傳動比為

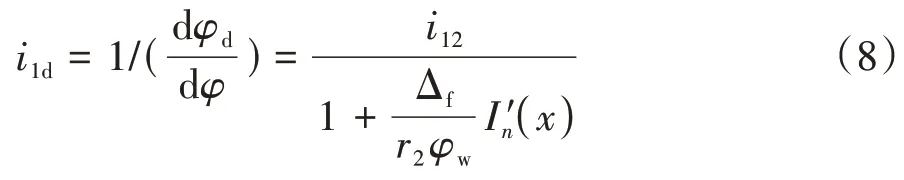
在式中，嚙入端修形量Δf、蝸輪分度圓半徑r2和工作半角φw均為常值且為正數.因此，工藝傳動比i1d與公稱傳動比i12的大小關系由決定.在圖2 中，為曲線的斜率，由此可知對應的轉角系數在x=-0.5 左右，在x=-0.5附近右側，＞0，i1d＜i12；在x=-0.5附近左側＜0，i1d＞i12.

2 高次方修形蝸桿傳動嚙合理論

2.1 坐標系的選取及直線刀刃方程

如圖3，直廓環面蝸桿的齒面是由直線刃車刀加工而成，與蝸桿相配對的蝸輪是由與蝸桿形狀相同的滾刀加工而成.

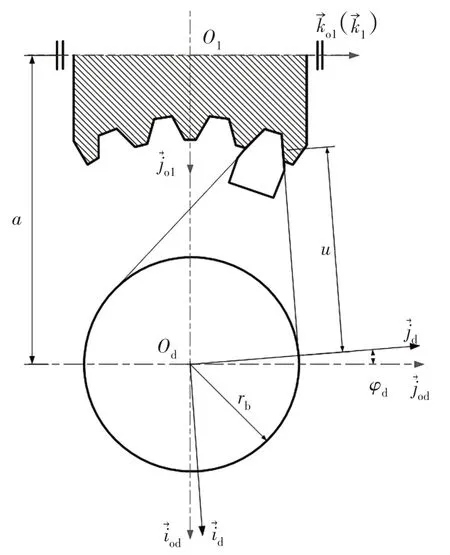
圖3 直廓環面蝸桿成型原理Fig.3 The forming principle of straight profile toroidal worm

圖3中u為直線刃車刀參數，由此可得刀刃直線方程

根據蝸桿副加工嚙合原理，可確定各坐標系的位置關系，建立如圖4坐標系系統.

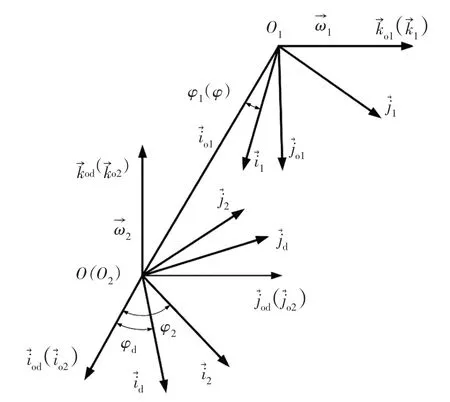
圖4 坐標系的位置關系Fig.4 The positional relationship of the coordinate system

對式（9）做旋轉矩陣變換得到σod中刀刃直線族方程為

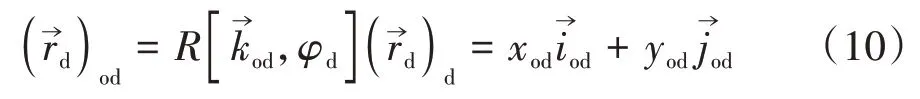
式中：xod=-ucosφd-rbsinφd，yod=-usinφd+rbcosφd，為繞旋轉的矢量矩陣［11］.進而由式（10）求得σ1中蝸桿螺旋面方程

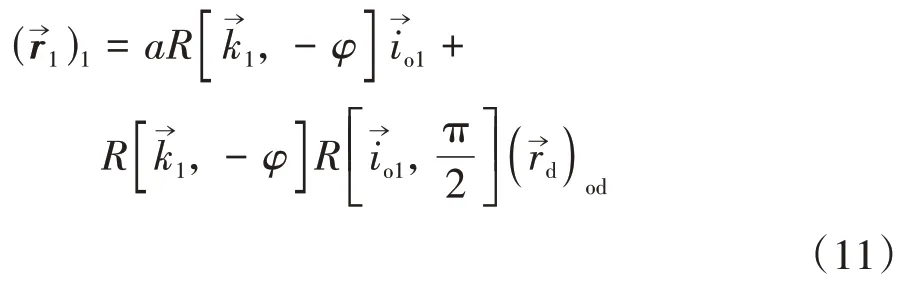
2.2 直廓環面蝸桿螺旋面不可展性的數學證明

σ1中蝸桿的螺旋面方程也可以寫成以下形式

其中

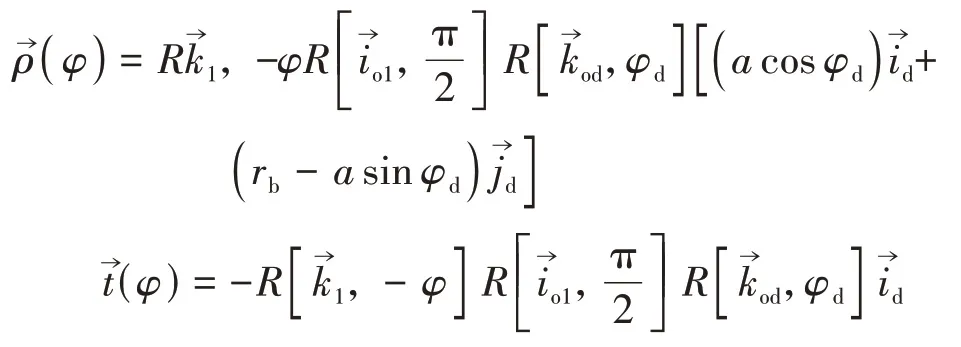
式（12）與直紋面的標準方程相符.在此基礎上證明其不可展.從式（12）計算導矢，分別令對φ求導

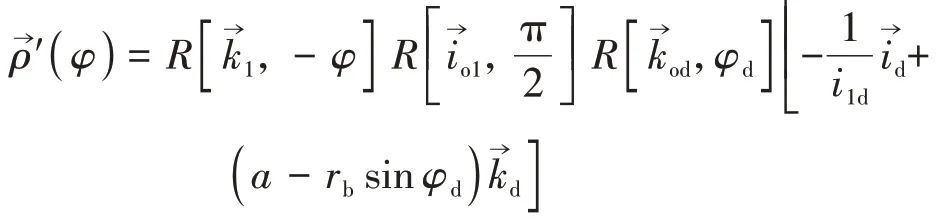
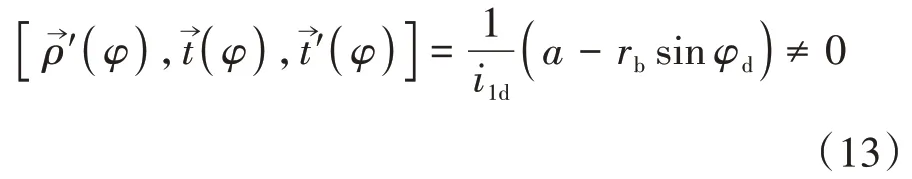
這與可展曲面的判定條件相悖，即直廓環面蝸桿的螺旋面為不可展.綜上可得，直廓環面蝸桿的螺旋面為不可展的直紋面.

2.3 蝸桿螺旋面的兩類基本量及曲率參數

由式（11）可得u、φ兩個方向偏導矢

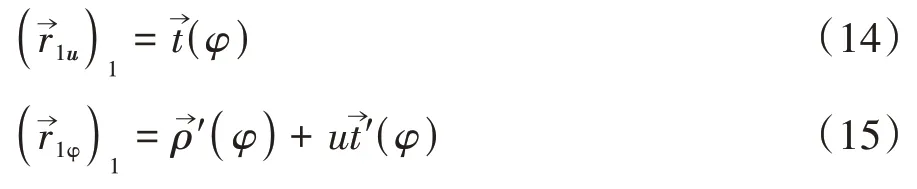
根據微分幾何理論求得直廓環面蝸桿螺旋面的第一類基本量為

由式（14）（15）及第一類基本量求得坐標系σ1中蝸桿的螺旋面單位法向量為

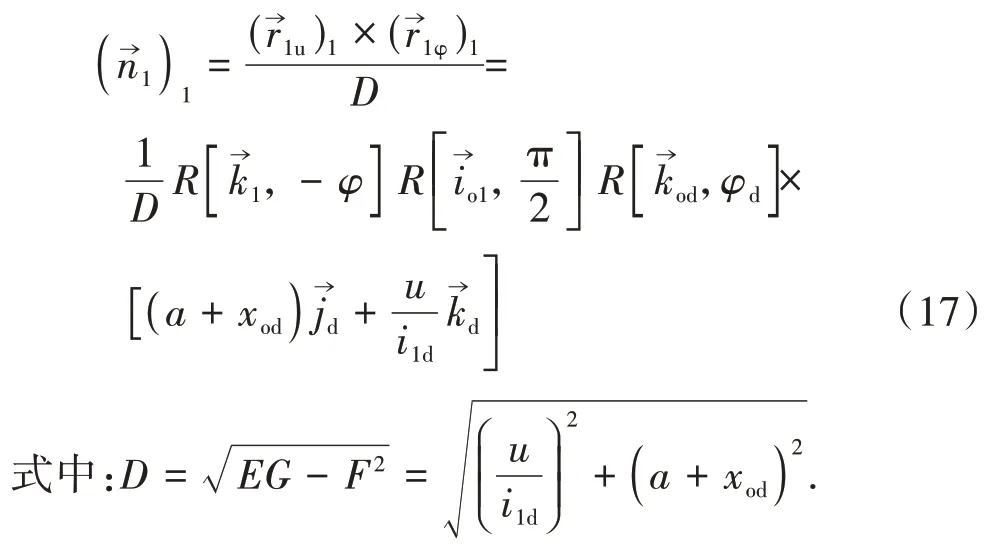
為計算螺旋面的第二類基本量，分別計算蝸桿螺旋面方程對u、φ的二階偏導矢

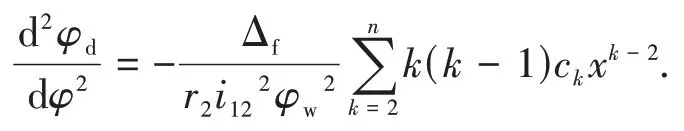
從式（17）（18）（19）和（20），可以計算出直廓環面蝸桿螺旋面的第二類基本量如下：

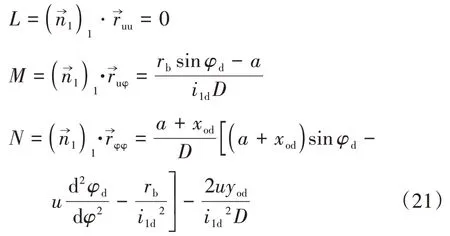
沿u方向的單位切向量和正交于的單位切矢量可表示為［12］

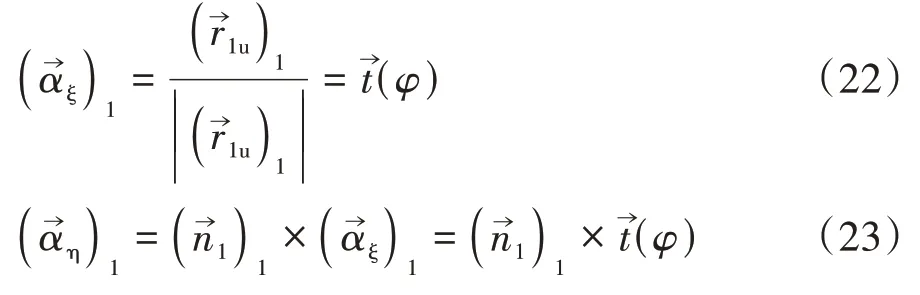
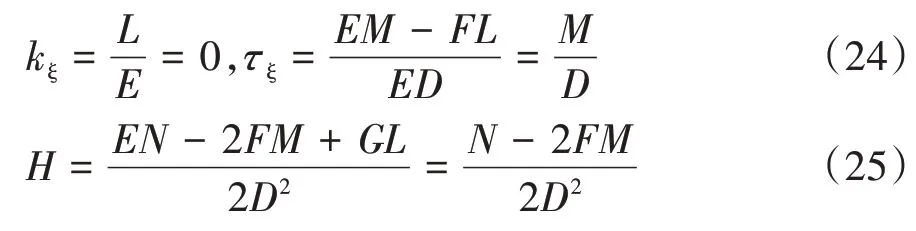
2.4 蝸輪的齒面方程及嚙合函數

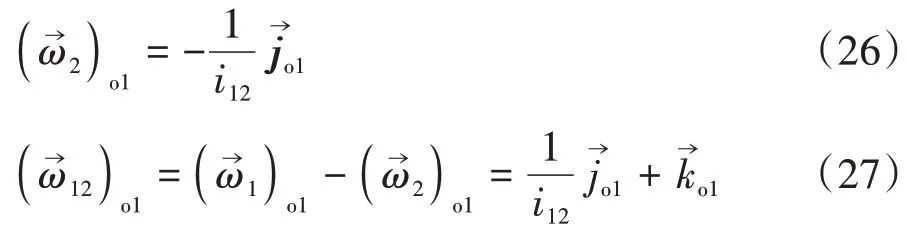
由旋轉變換得到σo1中蝸輪齒面生成面族方程

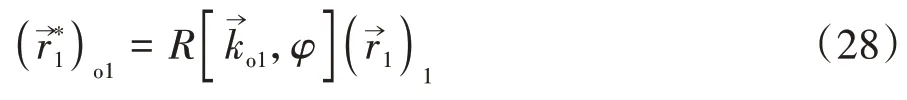
同理蝸輪齒面生成面族的單位法向量也可由旋轉矩陣變換得到

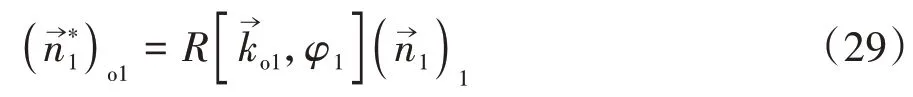
在σo1中蝸桿螺旋面和蝸輪齒面嚙合的相對速度矢量為

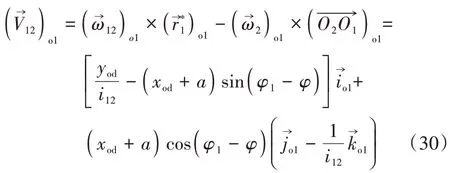
σo1中兩個單位切向量為

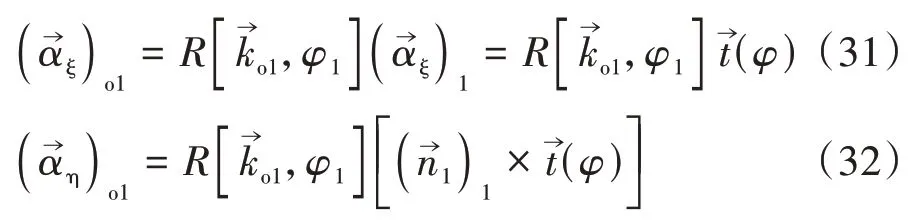
由式（29）和式（30）推導嚙合函數如下［13-15］：

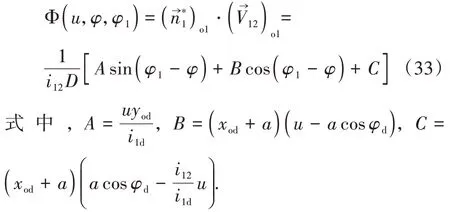
由蝸桿副滿足關系Φ(u，φ，φ1)=0可得

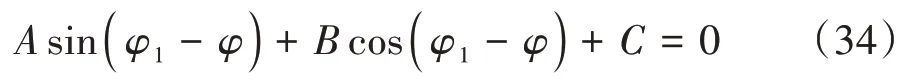
對式（34）進行三角變換

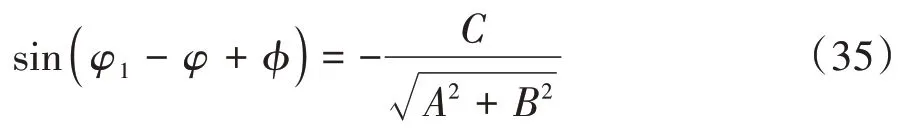
式中φ滿足以下關系：

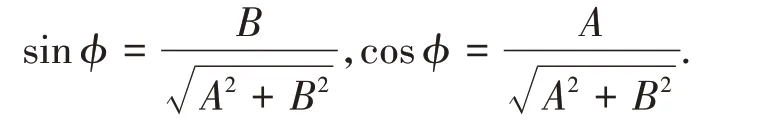
由式（35）得到一個嚙合周期內φ1的兩個解：

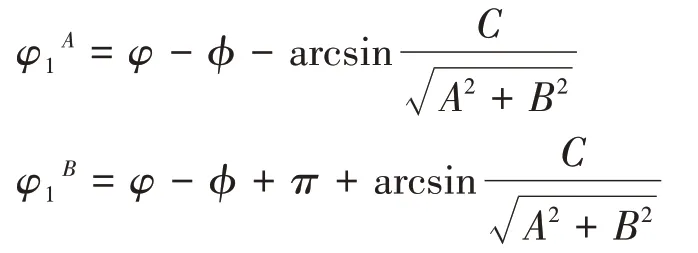
這兩個解分別表示在子共軛區ΣA和ΣB中φ1與u、φ的關系.在σ2中蝸輪齒面兩個子共軛區ΣA和ΣB的方程分別為

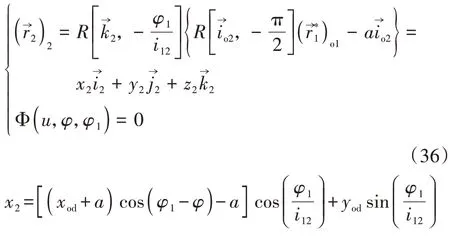
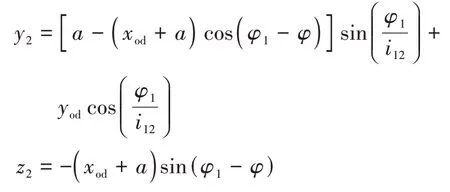
由式（33）對φ1微分得到直廓環面蝸桿副的嚙合極限函數為

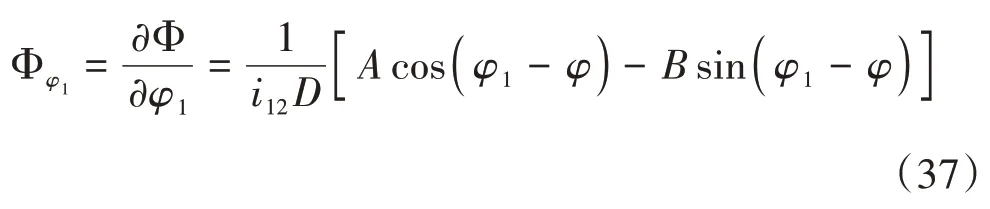
直廓環面蝸桿嚙合過程中的瞬時接觸線的法向量為

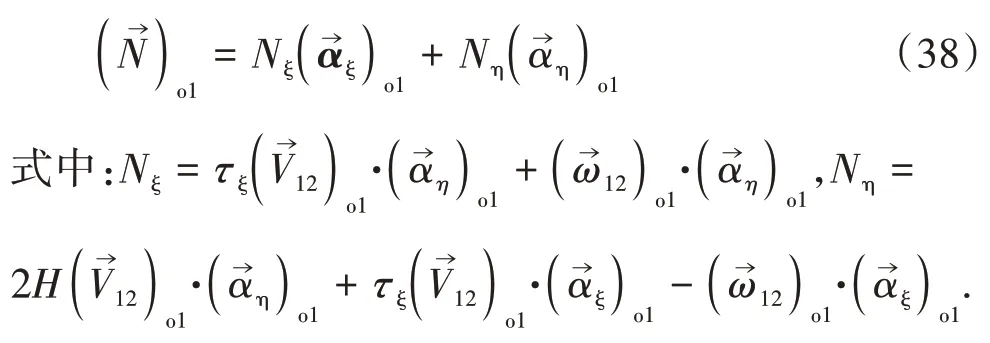
各項因式乘積的計算結果表示如下：

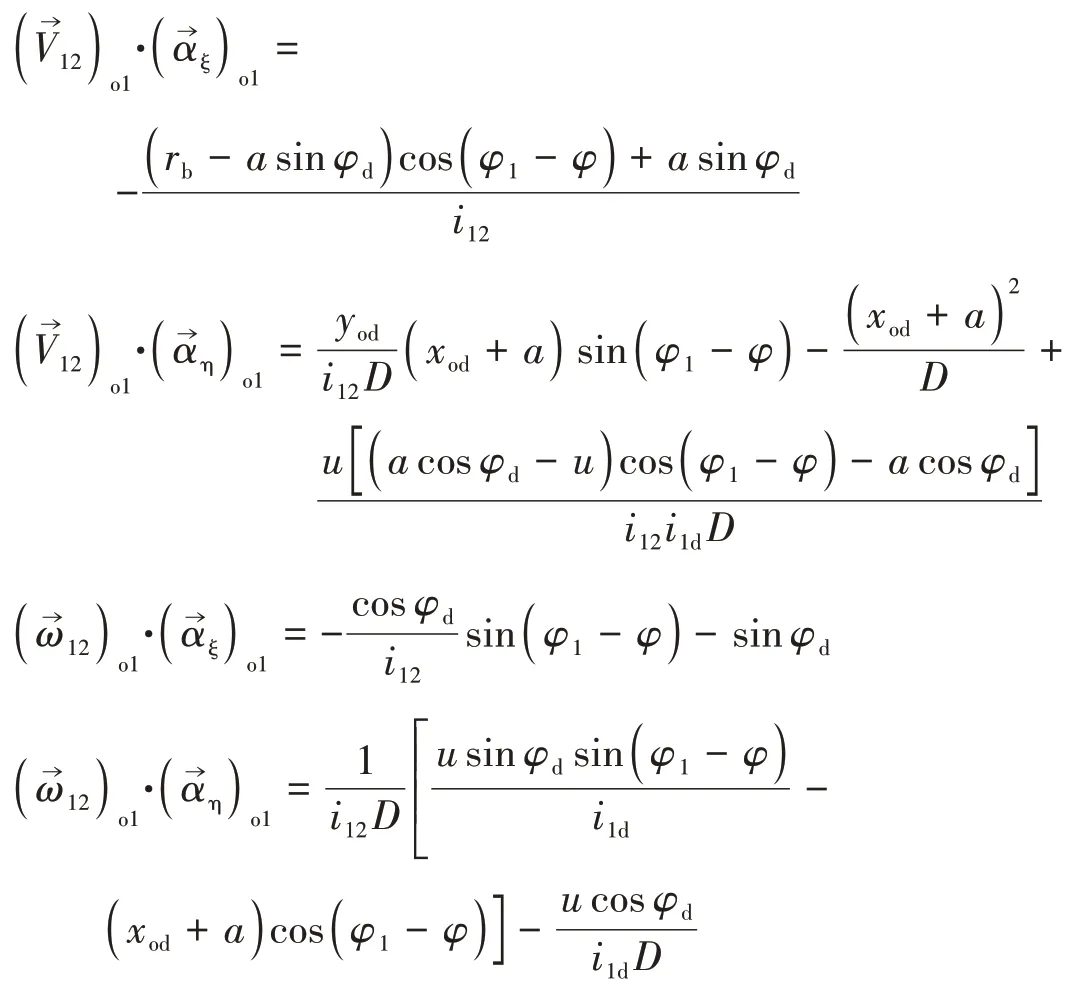
據式（37）（38）可求得曲率干涉界限函數為

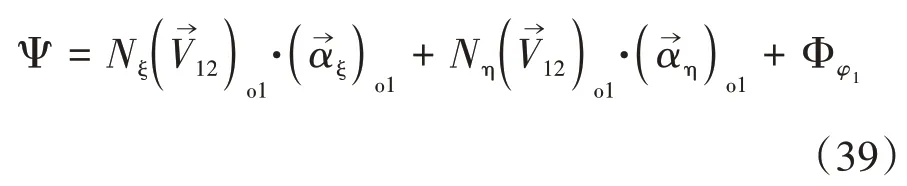
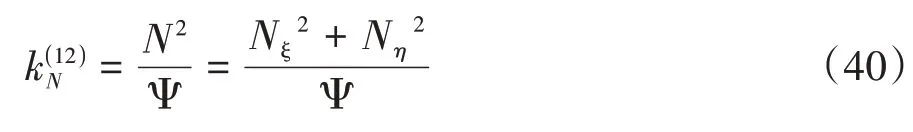
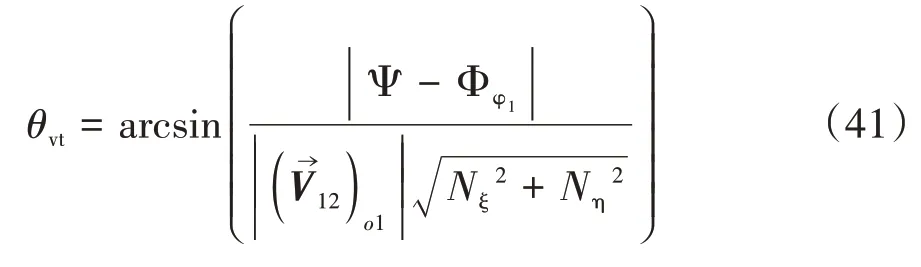
3 數值算例分析

仿真分析部分采用數值算例的蝸桿副參數為Z1=2，a=280 mm，i12=25.表4 中給出了算例所需參數的計算方法及其數值結果［16-17］.

表4 蝸桿副參數Tab.4 Worm pair parameters

3.1 原始型直廓環面蝸桿傳動的嚙合特性

圖5 基于蝸桿傳動嚙合理論，令i1d=i12可以得到無修形的原始型傳動.按表4 中的技術參數，繪出了原始型傳動的共軛區與接觸線.

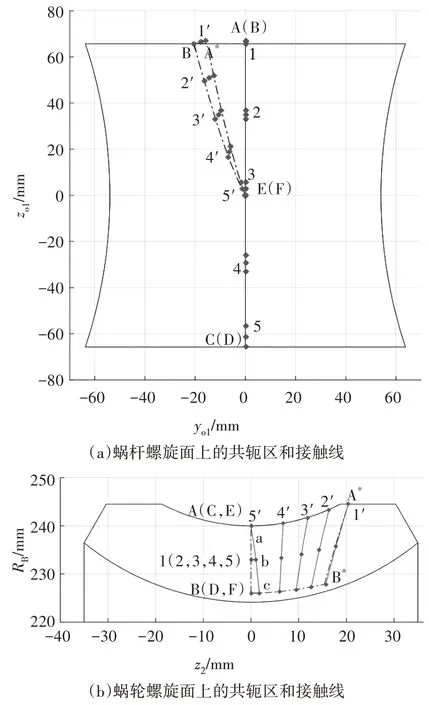
圖5 原始型直廓環面蝸桿嚙合特性Fig.5 Meshing characteristics of primitive straight profile toroidal worm

圖5（a）為蝸桿螺旋面在{O1；yo1，zo1}平面上的投影.區域ABCD為傳動副的共軛區ΣA，由式（34）可知，此區域內φ1=φ，AB線和CD線分別代表蝸桿的嚙入端與嚙出端.

圖5（b）為蝸輪齒面在{O2；z2，RB}平面上的投影，縱坐標RB=.AB線、CD線以及接觸線1-5重合，此區域退化為常接觸線.區域A*B*FE為傳動副的新接觸區ΣB.蝸桿螺旋面上的A*B*線代表共軛區ΣB的嚙入端，EF線為傳動副的曲率干涉界線，沿此線Ψ=0.同時EF線是共軛區ΣA與ΣB的公共邊界，構成傳動副嚙合界線，沿此線=0.因此在蝸輪齒面上EF線不起曲率干涉界線的作用，不引起曲率干涉，只對在蝸桿齒面上共軛區ΣB起嚙合界線的作用.沿EF線傳動副瞬時接觸線法矢量=0，因此它是瞬時接觸線的奇點軌跡.

分別在瞬時接觸線與蝸輪齒頂、蝸桿分度圓和蝸桿齒頂交點處選取3 個采樣點，計算采樣點誘導法曲率和滑動角θvt的數值結果列于表5中.數據表明，在整個ΣB區上，的值較小，即齒間的接觸應力小，油膜厚度相應增大［18］.且該子共軛區的θvt值較大，尤其在EF線附近數值接近90°，表明形成油膜的條件良好.

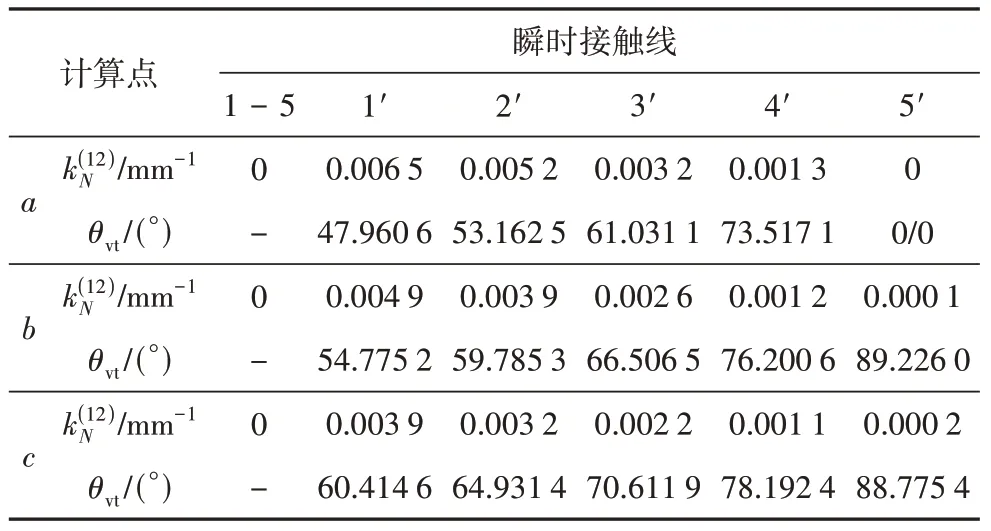
表5 原始型直廓環面蝸桿嚙合質量Tab.5 Meshing quality of original globoidal worm drive

3.2 高次方修形直廓環面蝸桿傳動的嚙合特性

為了防止過于繁冗，文中只給出3次、5次和7次曲線修形直廓環面蝸桿副的算例分析，如圖6-7 和圖8所示.

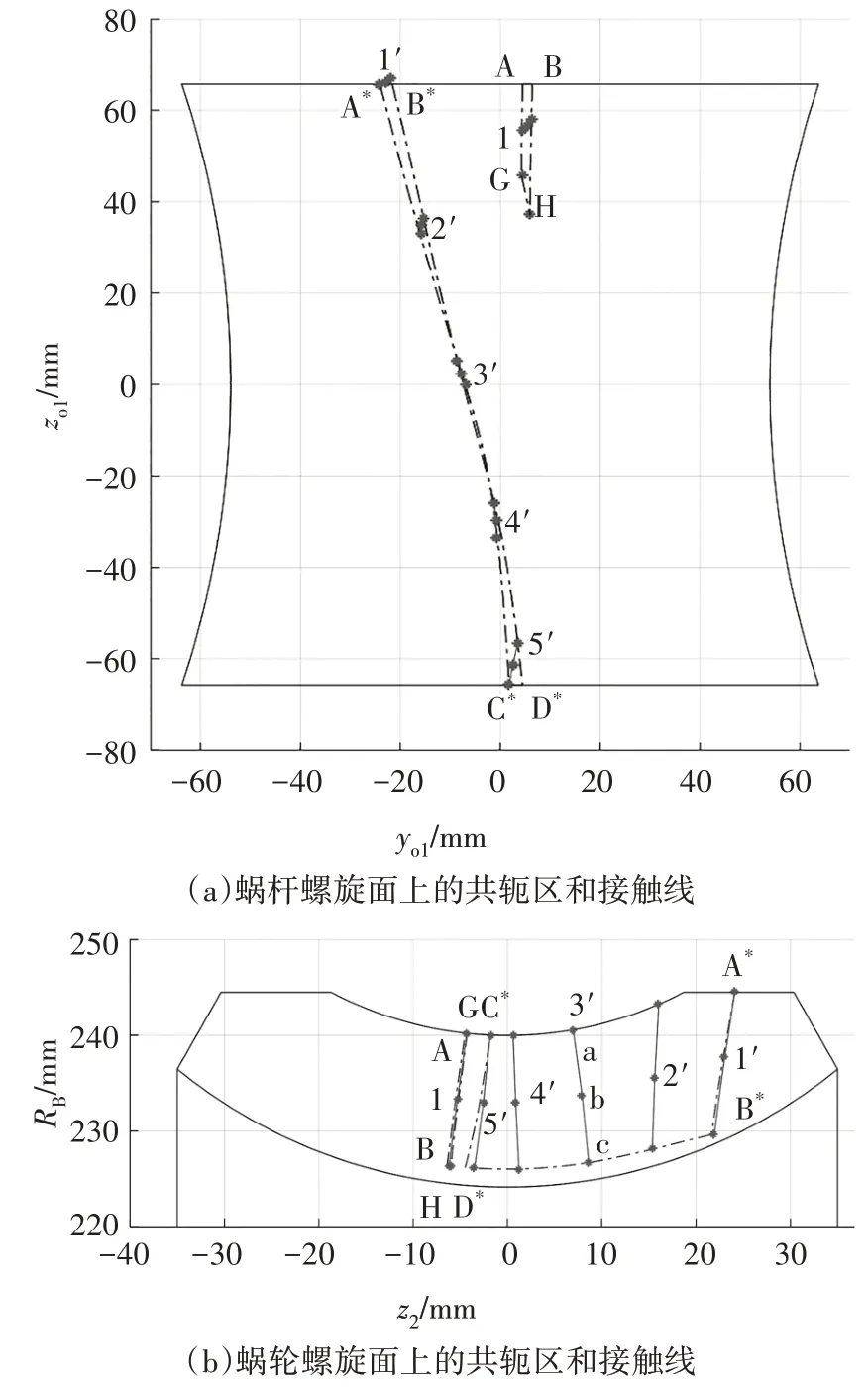
圖6 3次曲線修形后蝸桿副嚙合特性Fig.6 The meshing characteristics of the worm pair after cubic curve modification

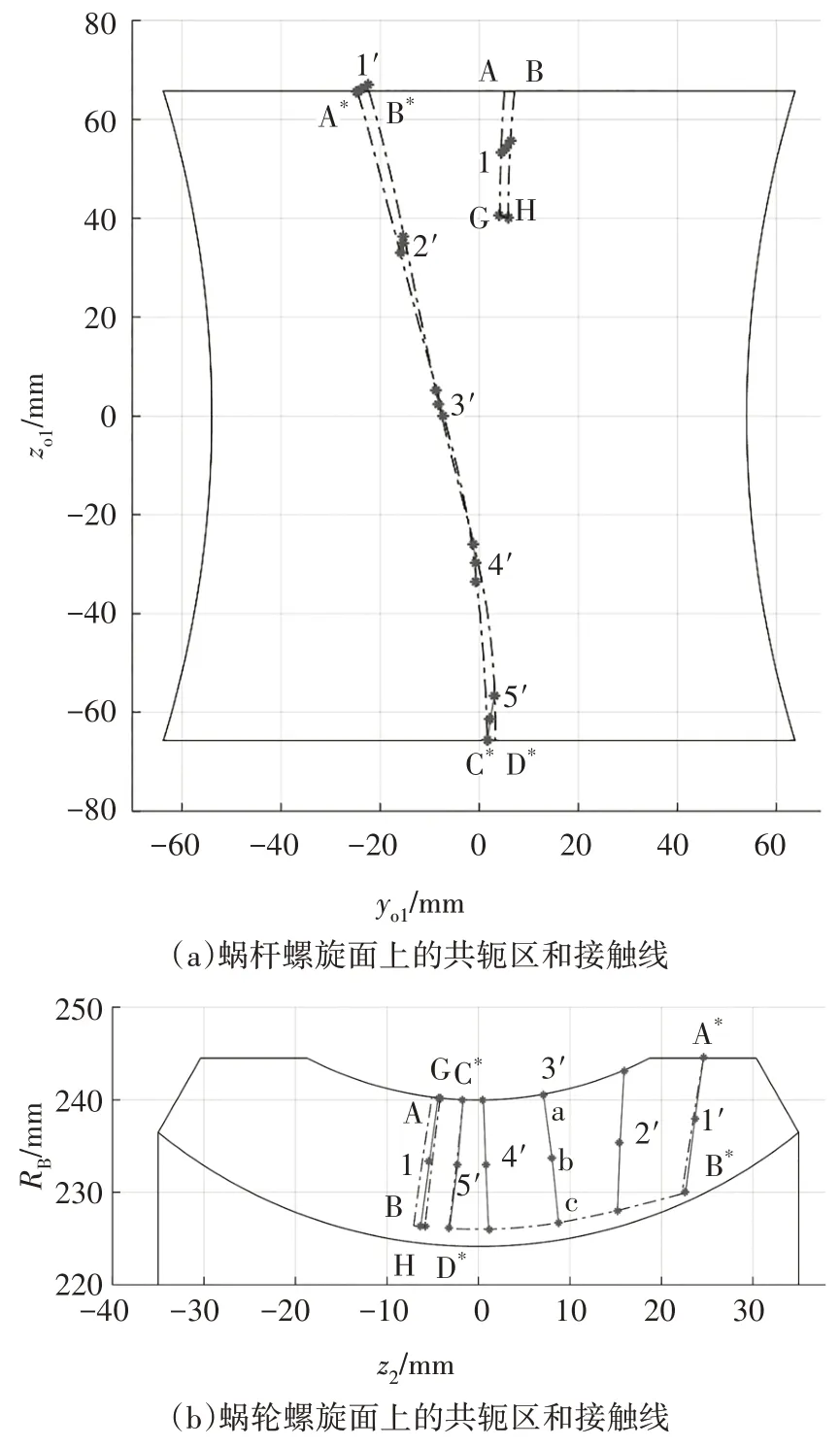
圖7 5次曲線修形后蝸桿副嚙合特性Fig.7 The meshing characteristics of the worm pair after the fifth power curve modification

圖6（a）和圖7（a）中，區域ABHG為子共軛區ΣA，相比于原始型直廓環面蝸桿副，ΣA區不再退化為常接觸線.但區域內存在曲率干涉界線GH，ΣA區不能貫徹蝸桿螺旋面的始終.區域A*B*D*C*為子共軛區ΣB，區域內的嚙合界線被消除，子共軛區ΣB擴大至蝸桿的嚙出端，C*D*線為嚙出端的反映線.這表明，修形后的蝸桿仍為全長可用，且在嚙入端附近實現部分雙線傳動.

圖6（b）和圖7（b）中，蝸輪齒面上的子共軛區ΣA和ΣB均增大.且與3 次修形相比，5 次修形的ΣA區更大一些.

表6和表7中，ΣA區的誘導法曲率值較小，滑動角θvt值較大，嚙合性能良好.相比于原始型直廓環面蝸桿，修形后ΣB區中的誘導法曲率并無明顯變化，滑動角θvt值略微增大，油膜的形成條件更良好.在曲率干涉界線GH上Ψ=0，誘導主曲率無限大，接觸應力也無限大，導致蝸桿副失效.

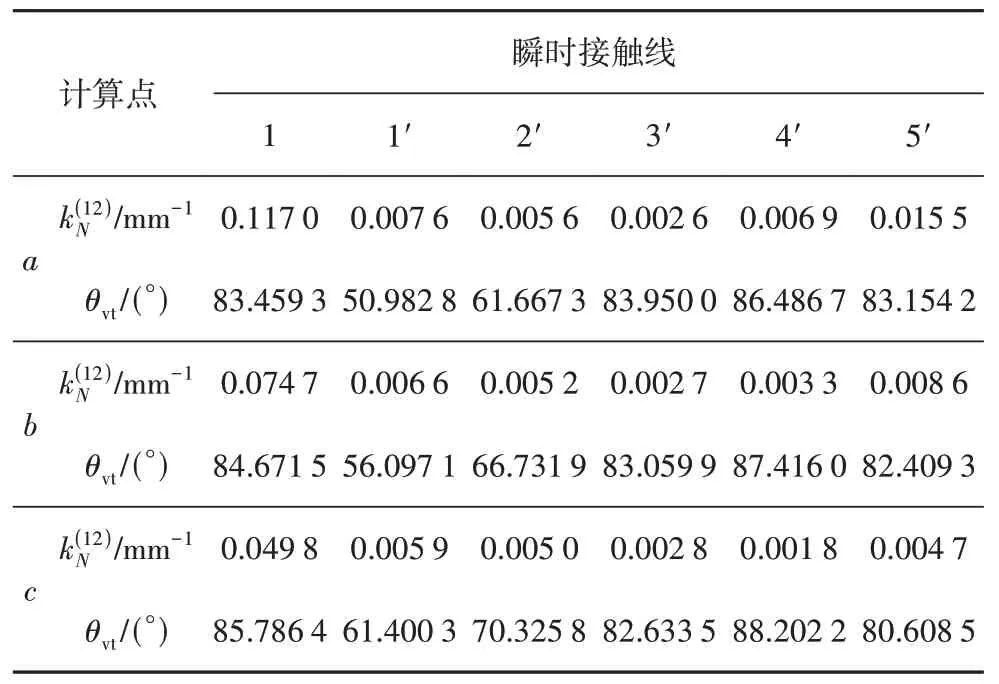
表6 3次修形直廓環面蝸桿嚙合質量Tab.6 Meshing quality of cubic curve modified globoidal worm drive

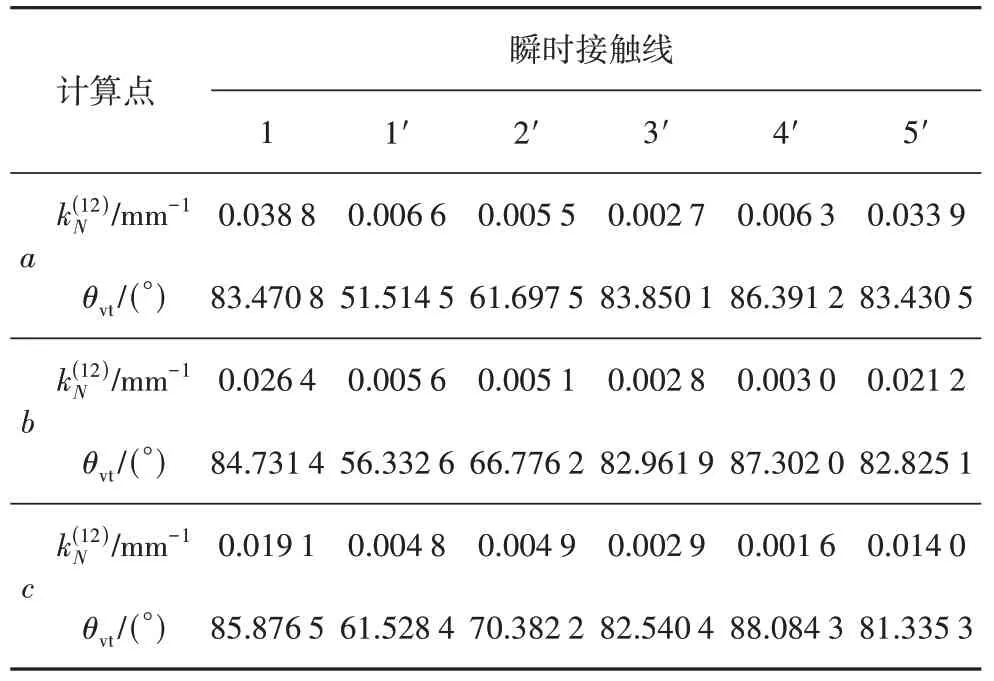
表7 5次修形直廓環面蝸桿嚙合質量Tab.7 Meshing quality of fifth power curve modified globoidal worm drive

提高修形曲線的擬合冪次后，子共軛區ΣA面積可以明顯增大，如圖8 所示，ΣB區的嚙出端反映線C*D*部分進入ΣA區.D*點的蝸桿轉角=1 357.7°，曲率干涉界線GH與蝸桿齒頂環面交點H的蝸桿轉角=286.19°.由于，說明ΣB區的蝸桿嚙出端反映線C*D*，在曲率干涉界線GH之后進入了共軛區ΣA，因此可以將其D*NH區域切除，也就是切除了曲率干涉界線GH靠近蝸輪齒根的部分NH.N點為蝸輪齒面上曲率干涉界線GH和C*D*線的交點，可通過求解由曲率干涉界線函數Ψ=0、蝸桿嚙出端邊界條件、以及ΣA和ΣB中N點在坐標系{O2；z2，RB}中橫縱坐標分別相等構成的方程組確定［19］.在蝸桿螺旋面上，D*N線是嚙出端在共軛區ΣA內的反映線，如圖8（a）所示.

位于該區上的瞬時接觸線1 是根據A點到G點蝸桿轉角的中間值得到的，其明顯更靠近邊界MNG，這說明ΣA區內瞬時接觸線分布不均勻，在邊界MNG附近瞬時接觸線更密集，在蝸桿副的傳動過程中接觸頻率更高，容易發生點蝕.

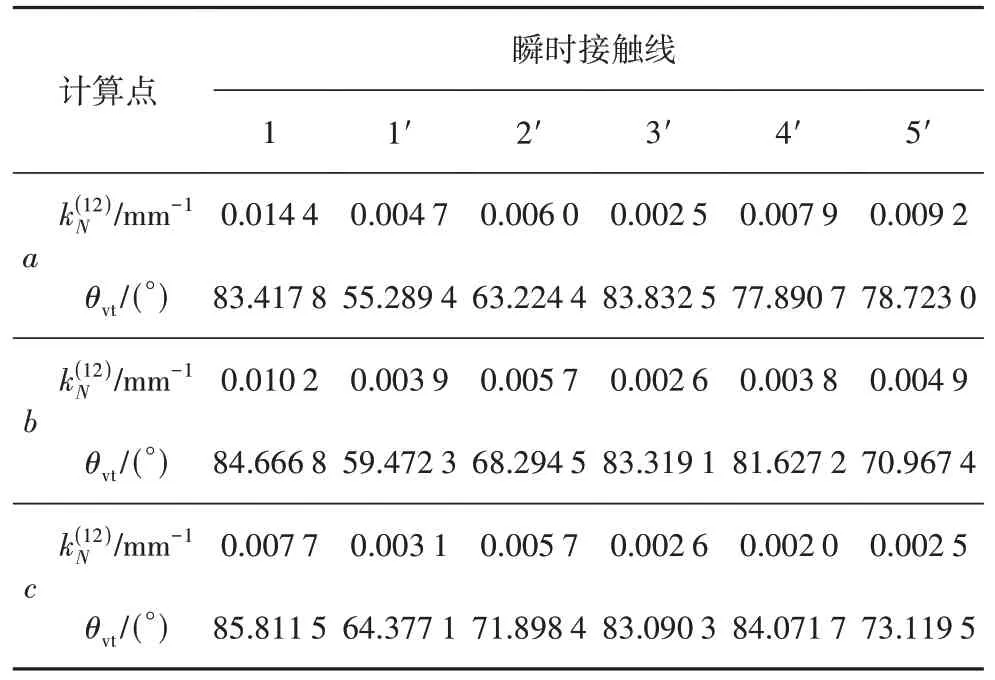
表8 7次修形直廓環面蝸桿嚙合質量Tab.8 Meshing quality of seventh power curve modified globoidal worm drive

4 結論

通過對修形數據無量綱化處理，推導出了更具普適性的高次方修形曲線函數，在此基礎上獲得了加工直廓環面蝸桿螺旋面的工藝傳動比的計算式.從而通過工藝傳動比，把修形曲線的影響引入嚙合分析的計算，改變了既有文獻中只考慮修形曲線對蝸桿齒厚影響的舊觀念.在這個意義上，基于修形曲線的修形應屬于變傳動比修形，工藝傳動比在本質上是時間的函數.數值結果表明，單純提高修形曲線函數的冪次，對于提升修形曲線擬合精度的作用是十分有限的.

基于旋轉變換矩陣，全面建立了高次方修正型直廓環面蝸桿傳動的嚙合理論，通過所得到的工藝傳動比公式，精確地考慮了修形曲線的影響，彌補了先前文獻在這方面的不足，嚴格論證了其蝸桿螺旋面為不可展的直紋面.

數值計算結果表明，高次方修形可以去除蝸輪齒面的常接觸線，并擴大接觸區，同時使蝸桿全長參與嚙合，且在入口部分保持一定長度的雙線接觸.高次方修形對誘導主曲率及滑動角等局部嚙合性能指標影響不大.主要不足之處是，蝸輪齒面中部靠近齒頂部位存在一定程度的曲率干涉，提升修形曲線函數的冪次，可以消減蝸輪齒面上曲率干涉界線的長度，但難以將其去除凈盡.

綜合考量，高次方修形需按一定規律改變加工蝸桿的工藝傳動比，在工藝方面相對比較復雜，又存在一定程度的曲率干涉，因此不宜單獨采用.