四輪驅動EV 自適應抗差無跡粒子濾波狀態估計
龍云澤,韋韜,封進,張瑞賓
(桂林航天工業學院汽車工程學院,廣西桂林 541004)
四輪驅動電動汽車(Electric Vehicle,EV)省去了傳統燃油車較長的傳動鏈,具有車輛底盤結構簡單、傳動效率高、驅動形式多樣化等優點,已成為全球汽車領域研究熱點[1].四輪驅動EV 的輪轂電機驅動力獨立可控,可實現整車多動力學狀態驅動,而整車狀態參數值的精確性是影響驅動模式優化及主動安全控制的關鍵因素.
近年來,改進卡爾曼濾波算法在四輪轂電機汽車整車狀態估計中得到了廣泛的運用[2].擴展卡爾曼濾波(extended Kalman filter,EKF)理論可實現整車非線性系統的狀態估計,但此方法需要計算復雜的雅可比矩陣,且存在線性化誤差的影響[3-4].無跡卡爾曼濾波(unscented Kalman filter,UKF)引入無損變換的思想,有效地克服EKF估計精度低、穩定性差的問題,在四輪驅動汽車狀態估計中得到了較好的應用,但其對整車參數估計結果在系統強非線性狀態下,精度會下降明顯[5].粒子濾波(particle filter,PF)的思想是利用粒子集來表示概率,從后驗概率中抽取的隨機狀態粒子來表達其分布,該濾波方法具有較強的非線性適應能力及多模態處理能力.但該方法在重采樣階段會造成樣本有效性和多樣性的損失,導致樣本貧化現象.國內外不少學者運用粒子群優化粒子濾波算法實現整車狀態估計,取得較好效果,但算法存在計算量較大,工程實現困難大的問題[6-8].無跡粒子濾波(unscented particle filter,UPF)算法運用無跡卡爾曼濾波方法生成建議密度函數,使先驗概率峰值與似然函數峰值具有良好的吻合性,達到降低粒子退化的目的,但其運算精度受系統噪聲不確定性的影響,且缺少自適應調整機制,不能對濾波增益及相關參數進行實時調節.
抗差估計濾波方法,可對濾波器參數進行實時調節,對干擾噪聲具有較好的自適應性[9].基于抗差濾波原理及無跡粒子濾波算法,構建自適應抗差無跡粒子濾波算法(adaptive robust unscented particle filter,ARUPF),通過整車動力學模型理論預測與實際測量融合的方法,實現四輪驅動電動汽車狀態的精確估計.為解決四輪驅動電動汽車狀態估計問題,建立整車七自由度整車動力學模型,通過引入權矩陣及自適應調節因子構建自適應抗差無跡粒子濾波算法,實現對整車狀態的精確估計,并運用CarSim 與Matlab/Simulink 軟件進行聯合仿真驗證該方法的有效性.
1 四輪驅動電動汽車動力學建模
從七自由度整車動力學模型、車輪運動學模型、輪胎模型三個方面搭建四輪驅動汽車動力學模型.通過魔術公式輪胎模型計算各輪胎縱向及側向驅動力,并結合七自由度整車動力學模型與車輪運動學模型進行整車動力學狀態分析[10].
1.1 七自由度整車動力學模型
建立四輪轂電機驅動車七自由度動力學模型,如圖1 所示.研究的目標為對整車行駛過程中縱向速度、側向速度、質心側偏角進行實時準確估計.因此模型考慮整車縱向運動、側向運動、橫擺運動及四輪轂電機轉動自由度.模型作了以下近似:1)忽略整車垂向運動、繞y軸的俯仰運動、繞x軸側傾3個運動的影響;2)忽略滾動阻力影響;3)忽略風阻影響;4)假設兩前輪具有相同的轉向角和側偏角;5)采用傳統的前輪轉向方式;6)假設兩后輪的側偏角一致;7)假設各輪胎動力學特性一致.七自由度四輪轂驅動汽車動力學方程如下[11-12].


式中;vx為整車縱向速度;vy為整車側向速度;γ為整車橫擺角速度;ax為縱向加速度;ay為側向加速度;Fxfl、Fxfr、Fyfl、Fyfr、Fxrl、Fxrr、Fyrl、Fyrr分別為左前輪縱向力、右前輪縱向力、左前輪側向力、右前輪側向力、左后輪縱向力、右后輪縱向力、左后輪側向力、右后輪側向力;M為橫擺力矩;β為質心側偏角;δf為前輪轉向角;m為整車質量;df、dr分別為前、后輪輪距.αfl、αfr、αrl、αrr分別為左前輪、右前輪、左后輪、右后輪輪胎側偏角.
1.2 車輪運動學模型
四輪驅動電動汽車車輪運動學模型為:

式中:Iw為車輪轉動慣量;ωfl、ωfr、ωrl、ωrr分別為左前輪、右前輪、左后輪、右后輪轉動角速度;Tfl、Tfr、Trl、Trr分別為左前輪、右前輪、左后輪、右后輪驅動轉矩;Tbfl、Tbfr、Tbrl、Tbrr分別為左前輪、右前輪、左后輪、右后輪制動轉矩;Re為車輪滾動半徑.
1.3 魔術公式輪胎模型
魔術公式輪胎模型能較好地模擬輪胎非線性動力學特性,得出各輪的縱向力與側向力.魔術公式輪胎模型公式如下:

式中:Fxij為車輪縱向力;Fyij為車輪側向力;B為剛度因子;C為曲線形狀因子;D為峰值因子;E為曲線曲率因子;λij為縱向滑移率;αij為側偏角.其中縱向滑移率λij分為驅動與制動兩情況[13]:

式中:re為車輪有效滾動半徑;ωij為車輪滾動角速度;vij為車輪中心運動速度.
2 ARUPF整車狀態估計算法
以七自由度汽車動力學模型為基礎,四輪驅動電動汽車行駛狀態估計原理如圖2 所示.基于ARUPF 算法,運用整車狀態預測值與傳感器觀測值相結合,實現對整車行駛狀態的實時估計[14].

圖2 整車行駛狀態估計算法結構原理Fig.2 Structure and theory of vehicle driving state estimation algorithm
傳統的粒子濾波算法存在迭代過程中粒子退化的缺陷,造成計算資源浪費、估計結果精度偏低等問題.為解決以上問題,常運用增加粒子數、重采樣、選擇合理的建議密度函數等方法對濾波算法進行優化.增加粒子數可有效緩解粒子退化,但增加了系統計算工作量.重采樣方法可增加粒子的多樣性,避免粒子退化.自適應抗差無跡粒子濾波算法利用無跡變換算法為每個粒子計算均值和協方差并建立合理建議密度函數,并結合抗差濾波估計算法自動調節增益矩陣及系統方差,使樣本點分布較好地與最大似然函數吻合.無跡粒子濾波算法易于工程實現,能有效減少系統計算工作量,其具體方法如下:
1)初始化,k=0,從先驗分布抽取初始狀態粒子.
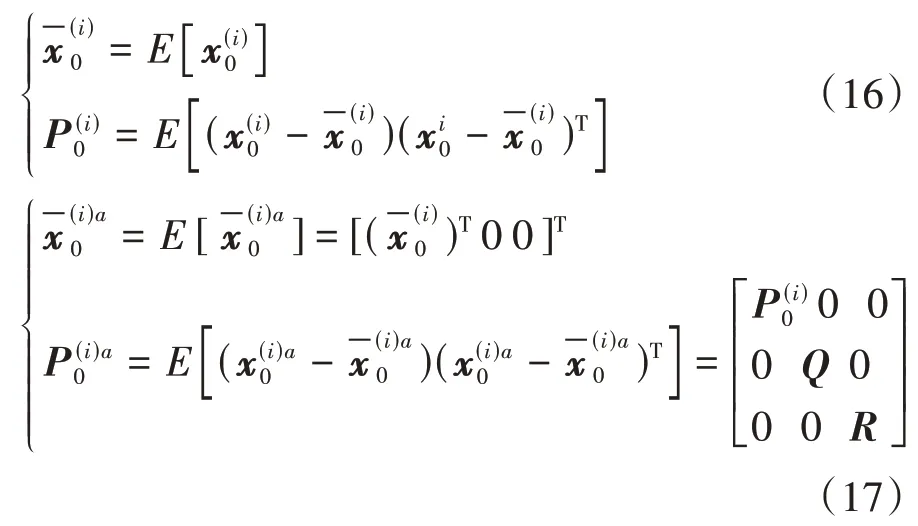
2)重要性采樣.運用無跡卡爾曼算法計算均值與方差.
(1)抽取Sigma點集合.

(2)對Sigma點集進行一步預測.

(3)融入觀測數據,更新Sigma點集均值、卡爾曼增益及協方差.

3)ARUPF 算法.ARUPF 算法基于抗差估計濾波理論,對動力學模型觀測量值異常情況加以控制,并構建自適應因子對動力學模型誤差加以控制.設為狀態向量的權矩陣,則等價權陣為.運用IGG(Institute of Geod?esy&Geophysics)方法產生等價權函數,其原理如下:

式中:Vk=為傳感器探測殘差值;調節因子參考取值范圍K0∈(1,1.5);調節因子參考取值范圍Kg∈(3,8).
令傳感器感知矩陣為Ak,根據權矩陣,對系統狀態向量進行更新.可得自適應抗差卡爾曼濾波的系統狀態解向量為:

式中:αk為自適應因子;調節因子c0參考取值范圍c0∈(1,1.5);調節因子c1參考取值范圍c1∈(3,8);tr為矩陣求跡運算符.
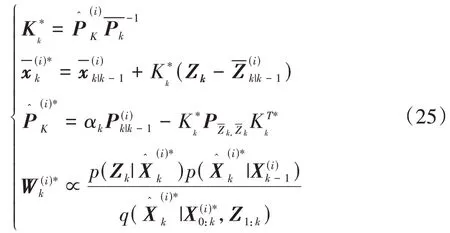
3 仿真實驗驗證
運用CarSim 與Matlab/Simulink 軟件進行聯合仿真實驗對估計算法進行驗證.CarSim 軟件專門針對車輛動力學特性搭建出各種車型動力學仿真模型,其模型的仿真性能接近于實車,仿真結果被國際眾多汽車制造商和零部件供應商所采用.在CarSim 軟件中搭建四輪轂驅動電動汽車模型,將其部分運行參數作為整車傳感器測量參數輸入Simulink 仿真軟件.在Simulink 軟件中搭建車輛動力學模型及ARUPF 濾波算法,進行車輛運行狀態估計,并將估計值與CarSim 軟件車輛模型進行對比驗證[15].整車關鍵參數如表1所示.

表1 整車動力學模型關鍵參數Tab.1 Key parameters of vehicle dynamics model
CarSim 整車模型選用B 型車,仿真實驗工況選用ISO雙移線實驗工況,車速為30 km/h,路面附著系數為0.6.所搭建CarSim 與Matlab/Simulink 聯合仿真模型如圖3所示.

圖3 聯合仿真模型原理圖Fig.3 Schematic diagram of joint simulation model
基于ARUPF 算法,選取所估計的狀態向量為x=[vx vy β]T.以Carsim 整車模型部分參數,作為傳感器所測得的車輛狀態真實值,輸入至Simulink 整車動力學模型,進行狀態預測.Carsim 整車模型的前輪轉角、車輪轉速、縱向加速度、側向加速度、橫擺角速度如圖4(a)~圖4(e)所示.將預測值與觀測狀態加入隨機噪聲,共同輸入ARUPF 濾波器進行狀態估計.將粒子濾波、無跡粒子濾波與自適應抗差無跡粒子濾波后整車狀態估值與理想值對比,所得結果如圖5(a)~圖5(c)所示.

圖4 車輛傳感器輸入參數Fig.4 Input parameters of vehicle sensors

圖5 基于ARUPF狀態估計仿真結果Fig.5 Simulation results based on ARUPF state estimation
由仿真結果可知,CarSim 軟件輸出的真實值與Simulink 中所搭建仿真動力學模型的ARUPF 狀態估計值相接近,驗證了動力學模型的正確性.PF 估計值在后期由于粒子退化的原因易造成較大的估計誤差,所采用ARUPF 狀態估計算法有效地解決了傳統粒子濾波算法樣本貧化造成的精度下降問題,其狀態估計的精度優于UPF 算法.所搭建ARUPF 濾波器針對過程噪聲的濾波效果較好,具有較好的自適應性及抗干擾能力.
4 結論
1)基于四輪驅動汽車結構特征及魔術公式輪胎模型,建立了前輪轉向的四輪分布式驅動電動汽車七自由度動力學模型.模型采用低成本傳感參數作為輸入量,實現對整車縱向車速、側向車速及質心側偏角的估計,具有實現成本低、工程易實現、抗干擾能力較強的優點.為四輪分布式驅動電動汽車狀態估計提供了一種新的思路.
2)給出了一種采用等價權矩陣解決四輪分布式驅動汽車傳感器數據粗大誤差干擾問題的新方法.運用IGG 方法產生等價權函數,通過自適應調節權矩陣,可有效抑制車輛傳感器檢測過程中因非線性因素造成的隨機誤差,減小干擾造成的數據失真影響,提高了整車狀態估計精度.
3)運用自適應抗差濾波原理,結合無跡粒子濾波算法,提出一種新的四輪驅動電動汽車整車的狀態估計方法.該ARUPF 方法具有噪聲濾除效果好、精度高等優點.搭建CarSim 與Matlab/Simulink 聯合仿真平臺,對整車狀態估計進行仿真分析驗證.仿真結果表明,基于ARUPF 算法的整車狀態估計具有精度高、抗干擾能力強、穩定性好的特點.

