一種改進的模逆算法與硬件實現

胡錦，李勇彬

（湖南大學物理與微電子科學學院，湖南長沙 410082）

RSA 密碼和橢圓曲線密碼是目前使用最廣泛的公鑰密碼算法.隨著物聯網的發展，用戶信息安全越來越重要，例如現今高速發展的智能汽車，安全性和實時性要求極高，軟件實現加密算法的方式已經無法滿足需求，采用硬件方式實現算法是發展的趨勢.模逆算法是公鑰密碼體系中的核心算法［1-2］，尤其在橢圓曲線密碼體系中［3］，也是最復雜［4］和最消耗時間的算法之一［5］.在RSA 密碼算法中，生成密鑰對時，需要計算d=e-1modφ，其中e表示公鑰，滿足1＜e＜φ且gcd（e，φ）=1，φ表示歐拉函數，d表示私鑰.為了安全，φ至少為1 024 位，用軟件實現模逆運算，運算量大，運算時間長，效率低［6］.在橢圓曲線密碼算法中，進行點加［7］、點乘和倍點運算時，用雅可比坐標進行坐標變換［8］也只能減少模逆運算使用的次數而不能完全避免.本文在現有的二進制模逆算法基礎上進行了改進，提出了一種在求逆過程中同時可以求取最大公約數的算法.此外，出于對實現算法的硬件資源考慮，對算法做了優化，最后通過VERILOG 語言進行硬件實現.

1 算法介紹

1.1 二進制模逆算法

二進制模逆算法原理是根據貝祖等式gcd（a，b）=gcd（b-a，a）=ax+by 推導得出.目前常用的模逆算法還有擴展歐幾里得算法［9-10］，但是由于算法中每步都要用到除法操作，開銷很大［11］，尤其在進行大素數模逆運算時缺點更突出.算法1 只用到了移位操作和減法運算，比擴展歐幾里得算法更加高效.

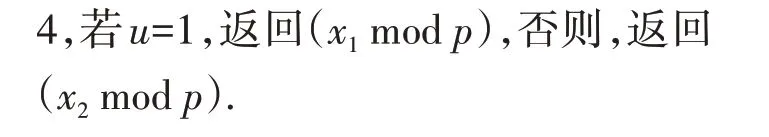
1.2 改進的模逆算法

算法1 有一個缺陷是無法判定輸入的兩數是否互質，如果gcd（a，p）不等于1 時，再用算法1 計算就會得到錯誤的結果，或者說算出的結果是沒有意義的.結合stein 算法［11］，可以將上述算法改寫為算法2，算法2 在模逆運算的同時可以求解最大公約數gcd（a，p），從而保證模逆運算的結果是在gcd（a，p）=1 的情況下得到的正確結果.在算法1 中可以看出，循環計算時u和v的計算基本上是一致的，為了節省資源，可以進行進一步優化.由于算法2 中的步驟3和步驟5.2 保證u和v每次循環最多只有一個為偶數，利用這個特點可以去掉u的循環.

2 算法硬件結構框圖

模逆算法主要通過狀態機來控制算法流程，通過ram 存儲大量的中間數據，圖1是模逆算法硬件結構框圖，主要分為兩個模塊，INV_FSM 模塊是狀態機模塊，INV_CAL是模逆算法的運算模塊，受狀態機模塊的調度.ram 為偽雙端口ram，主要用來存儲在運算過程中產生的中間數據和運算結果.

圖1 模逆算法硬件結構框圖Fig.1 Modular inversion algorithm hardware structure block diagram

2.1 算法狀態機

圖2 是模逆算法的狀態轉移圖，嚴格控制模逆算法的運算流程.該狀態機共有9個狀態，IDLE是空閑狀態，開始運算時，進入SHIFT狀態，SHIFT狀態完成x和y同時向右移位（即除以2），g向左移位，直到x和y不同時為偶數.LOAD 狀態主要完成u、v、A、B、C、D數據的裝載.INV_CAL 狀態完成模逆算法的主體運算直到v等于0 時才跳出該狀態.在GCD_CAL狀態中完成gcd（a，p）計算，在GCD_CAL 狀態計算完成后判斷A的極性進行狀態跳轉.若A為負數，則跳轉到A_NEG 狀態進行A+y運算，直到A為正數，則跳轉到DONE狀態；若A為正數，則跳轉到A_POS1狀態進一步判斷A是否大于y，若A小于y，則跳轉到DONE 狀態，若A大于y則跳轉到A_POS2 狀態進行A-y運算，直到A小于y，然后跳轉到DONE 狀態，模逆運算完成，最終回到IDLE狀態.

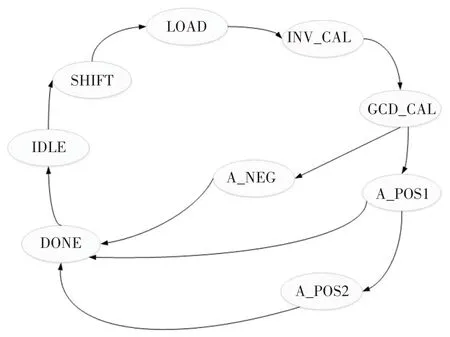
圖2 模逆算法狀態轉移圖Fig.2 State transition diagram of modular inversion algorithm

2.2 算法運算模塊

算法運算模塊主要功能是在狀態機的控制下進行數據的運算.從算法2 中可以看出，求逆的過程需要用到大數加法和大數減法，還需要進行兩數大小判斷和移位.大數加法和大數減法可以通過算法3和算法4 實現，兩數的大小比較可以通過使用大數減法的借位信號來判斷.圖3 是運算模塊主要運算電路，data_v和data_u通過mux 來進行選擇，mux 的選擇信號通過比較data_u和data_v的大小得到，data_c和data_a、data_b和data_d類似.從圖3 中可以看出：改進后的算法使用mux 可以進行u和v的選擇，從而實現資源的復用，減少了資源的消耗.運算的中間結果和運算結果保存在ram中.

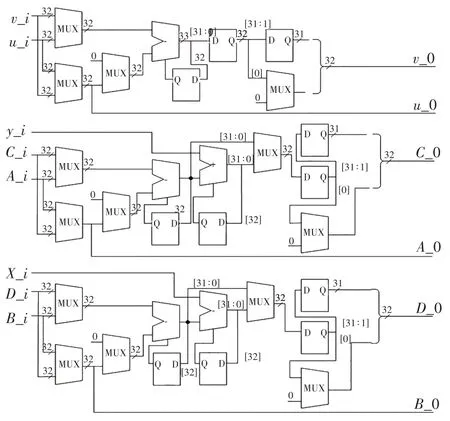
圖3 算法模塊電路圖Fig.3 Algorithm module circuit diagram

該電路中輸入數據都是以32 位為最小輸入單元，如果進行1 024 位的模逆運算，此電路需要計算32 次，可以看出此電路其實還可以實現2 048位甚至更大的模逆運算.需要注意的是.計算的位寬越大，需要保存的中間數據也越多，ram的容量就需要越大.

3 結果與分析

通過VCS 對該電路進行功能仿真，如圖4 所示.模逆算法電路能正確計算出最大公約數和模逆運算的結果，將計算的結果保存在ram 中.仿真結果表明：該設計可以正確進行32～1 024 bit的模逆運算.

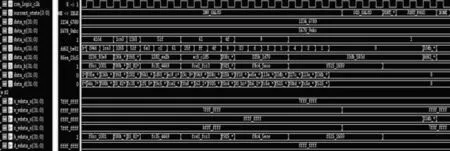
圖4 算法功能仿真圖Fig.4 Algorithm function simulation diagram

使用Xilinx virtex-II FPGA 開發板進行了板級驗證，驗證了該設計的正確性.表1 列出了該設計與同類設計的資源消耗和性能比較.表格中的時間為計算256 bit模逆運算使用的時間.

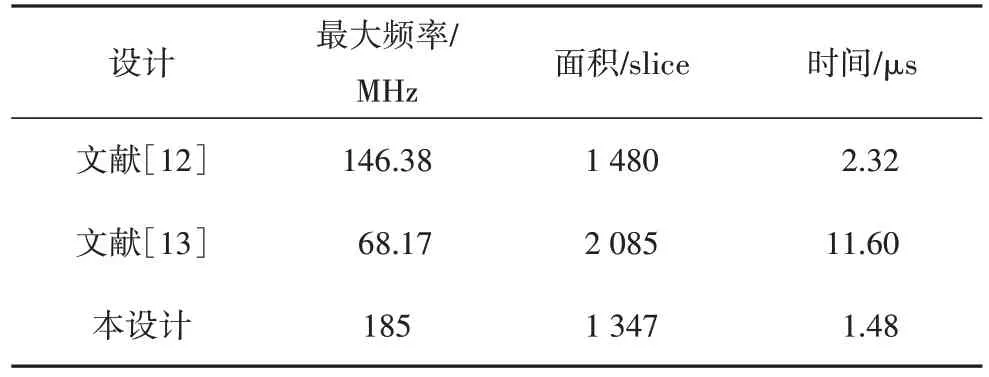
表1 FPGA結果對比Tab.1 FPGA result comparison

該設計應用于一款汽車安全芯片的PKI 模塊，用于實現RSA 和SM2 算法.圖5 為該安全芯片的版圖，采用UMC 55 nm 工藝進行流片，該芯片總面積為10 mm2，在工作電壓3.3 V，時鐘頻率為200 MHz 時，功耗僅為30.2 mW，流片測試結果表明，芯片達到設計指標要求.

圖5 芯片版圖Fig.5 Chip layout

4 結語

本文提出了一種在現有二進制模逆算法的基礎上進行改進的算法.該算法不僅可以進行模逆運算，還同時可以計算最大公約數，并且在算法上進行了優化，減少了算法實現的資源消耗，最后通過VERILOG 語言實現了該算法.該設計電路結構簡單，可擴展性強.最后該設計采用UMC 55nm 工藝進行流片，流片測試結果表明，芯片達到設計指標要求.