淺議與平面向量最值問題有關的幾種題型

■陳澤剛 杜海洋

平面向量中的最值問題是一種典型的能力考查題，它能有效地考查同學們分析問題和解決問題的能力，體現了高考在知識交匯處命題的思想。下面就平面向量最值問題有關的幾種題型舉例分析。

題型1：與數量積有關的最值問題

例1如圖1，扇形OAB的半徑為1，圓心角為，P是上的動點，則的最小值為_____。

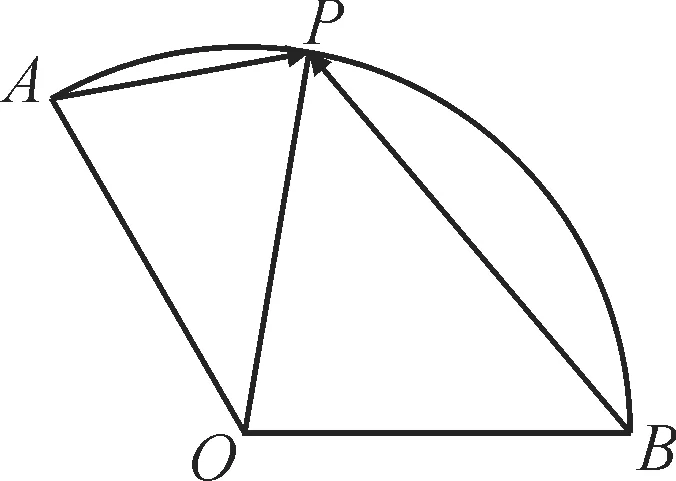
圖1

題型2：與模長有關的最值問題

題型3：與三角形有關的最值問題

題型4：與二次函數有關的最值問題

例4在△ABC中，AC＝1，BC＝2，∠ACB＝60°，點P是線段BC上一動點，則的最小值是____。

分析：建立直角坐標系，根據題意求得各點坐標，利用向量的坐標運算求得數量積，再結合二次函數求出最小值。

解：在△ABC中，由余弦定理得AB＝。由此可知△ABC是直角三角形。

以點A為坐標原點，AB所在直線為x軸，AC所在直線為y軸，建立平面直角坐標系xAy，如圖2所示。

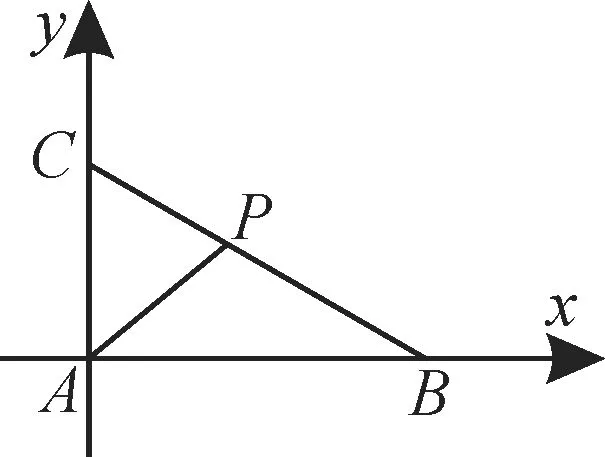
圖2

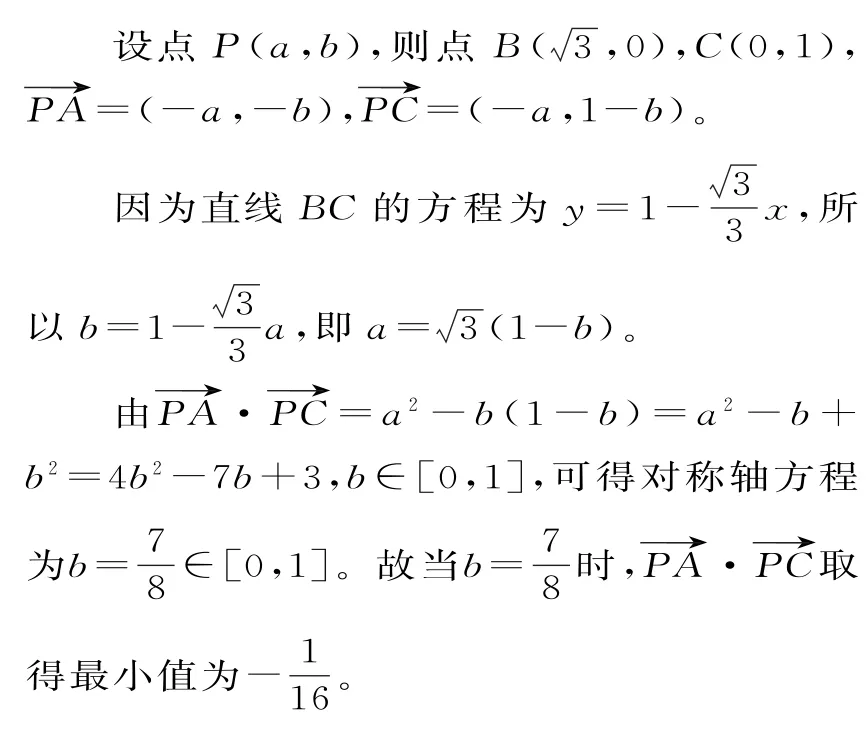
題型5：與基本不等式有關的最值問題

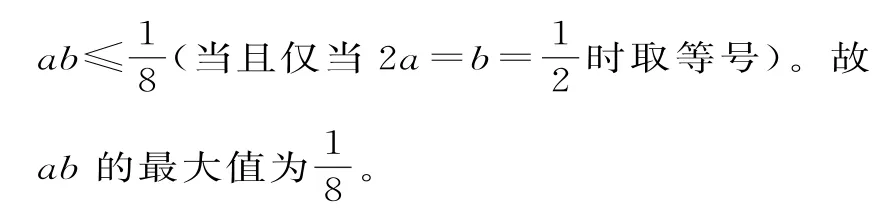
題型6：與三角函數有關的最值問題

小結：平面向量中的最值問題的求解通常有兩種思路:一是“形化”，即利用平面向量的幾何意義，將問題轉化為平面幾何中的最值問題，然后根據平面圖形的特征直接進行判斷；二是“數化”，即利用平面向量的坐標運算，將問題轉化為代數中的函數最值問題。