函數型Logistic回歸模型研究與應用

鄧 楠，羅幼喜

(湖北工業大學理學院，湖北 武漢 430068)

隨著在許多領域對數據質量的要求都越來越高，對數據的分析也從低頻數據分析向高頻數據分析進行跨越，但在很多情形，我們獲得的數據都為離散的數據，無法完全捕捉數據的信息。基于此，Ramsay于1982年提出了函數型數據分析(FDA)[1]。與傳統數據分析相比，FDA具有更多優越性，它通過對數據進行曲線性質的分析進而挖掘出更多重要的信息。在函數型數據分析中，函數型Logistic回歸是函數型線性回歸模型的一個重要應用。它針對響應變量為二分類數據，協變量為函數型數據建立回歸模型，利用樣本曲線的信息來預測某件事情發生的可能性，通過函數型變量隨時間的變化預測二元響應變量的變化。在國外，Ratcliffe等[2]基于模擬的胎兒心率軌跡構建了函數型Logistic回歸模型，將函數協變量和回歸函數用傅里葉基函數進行展開，對極大似然估計的計算使用改進的Fisher評分算法，并將此模型應用到胎兒出生風險預測。Kim等[3]考慮若函數數據高度混合，則基于整個區域的分類是無效的，因此提出了基于區間的函數型數據分類方法。該方法利用融合的Lasso懲罰自動選擇函數數據中信息最豐富的片段，同時利用函數邏輯回歸對選擇的片段進行分類。Denhere[4]考慮了當存在異常曲線時對未加處理的數據進行函數型主成分Logistic回歸不能得到良好的結果，提出了一種基于穩健主成分的函數型Logistic回歸模型。Mousavi等[5]則對許多情況下對函數協變量(作為輸入)和二元響應(作為輸出)之間的關系感興趣，由此通過3種方法對該模型的參數估計結果進行比較，并判斷這些方法正確分類的能力。在國內，王惠文等[6]針對同時包含數值型多元變量和函數型協變量的廣義線性回歸模型，采用非參數方法得到了參數部分和非參數部分的估計量，并給出了一種重加權算法進行參數求解，解決了含數值型和函數型混合數據類型自變量的回歸問題，由此擴展了函數型線性模型的應用范圍。孟銀鳳等[7]針對傳統函數Logistic模型泛化性能不高的問題，通過求解優化問題提出了線性正則化的函數Logistic回歸模型。梳理文獻發現，盡管已有文獻給出了函數型Logistic回歸模型的不同分析方法和應用實例，但通過貝葉斯方法對其分類性能的研究還較少。Crainiceanu等[8]曾介紹了在貝葉斯框架下函數型數據的分析方法，使用WinBugs對函數型數據進行分析，但未研究Logistic回歸模型的分類性能，Zhu等[9]則提出了針對二元響應變量和多元函數型協變量的貝葉斯變量選擇模型，并將其應用于宮頸癌診斷，但其對函數型Logistic回歸模型進行Probit變換時，未考慮Logit變換，因此本文考慮在貝葉斯框架下對函數型Logistic回歸模型進行Logit變換并對其分類性能進行研究。

1 函數型Logistic回歸模型

yi=πi+εi,i=1,2,…,N

(1)

其中：

πi=P[Y=1|]xi(t):t∈T}]=

i=1,…,N

(2)

α為實數參數，β(t)為參數函數，εi(i=1,2,…,N)為N個獨立且均值為零的隨機擾動項。等價地，通過Logit變換，式(2)可以表示為:

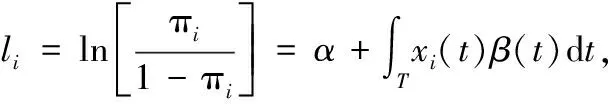
i=1,…,N

(3)

假設選取K個主成分基函數對回歸系數函數β(t)和函數數據x(t)進行展開，則

(4)

(5)

寫成矩陣形式表示為：l=α1+Cb，其中b=(b1,…,bK)T，1=(1,1,…,1)T，C=(cik)N×K為函數主成分得分，其計算方法為：

且滿足

從而在獨立條件下，模型的似然函數可以表示為：

(6)

2 基于Polya-Gamma變換的條件后驗分布推導

雖求得函數型Logisic回歸模型的似然函數，但由于一般先驗和模型似然函數的非共軛性較難求得參數后驗，因此考慮通過引入Polson[13]等提出的Polya-Gamma數據增強算法。Polya-Gamma數據增強算法對于不同模型都求得了更簡單且有效的后驗分布。該數據增強算法表示為：

記ω～PG(b,0),b>0表示服從參數為(b,0)的Polya-Gamma分布，其密度函數

則對于所有a∈R，有下列恒等式成立：

(7)

其中，κ=a-b/2，且p(ω∣ψ)～PG(b,ψ)。該數據增強算法有效規避了常用先驗分布與函數型Logistic回歸模型似然函數的非共軛性，從而在Polya-Gamma變換下，函數型Logistic回歸模型的似然函數可以改寫為：

(8)

(9)

則b的條件后驗可表示為：

(10)

即b,ω的聯合后驗為：

(11)

P(ωi|·)=PG(1,ηi)

(12)

由

(13)

(14)

則α得條件后驗為：

(15)

(16)

1)ωi|else～PG(1,ηi)，其中ηi=αi+cib；

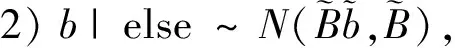
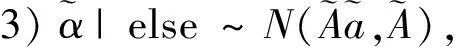
3 數值模擬

3.1 數據生成

首先生成獨立同分布的函數型隨機變量xi，再根據函數型Logistic回歸模型生成響應變量yi。該數據生成方法仿照文獻[5]設計，具體數據生成為：

i=1,2,…,150,j=1,2,…,256,tij∈[0,10]

(18)

i=1,2,…,150

(19)

其中β(t)為區間T=[0,10]上的已知函數，考慮β1(t)=sin(tπ/3)，β2(t)=-d(t∣2,0.3)+3d(t∣5,0.4)+d(t∣7.5,0.5)，其中d(·∣μ,σ)為服從均值為μ方差為σ的正態分布，采用主成分基函數進行擬合，模擬結果如圖1所示。在這里α設為0.5，使用截斷點0.5作為分割，即

則Y=1，否則Y=0[14]，圖2為參數函數為β1(t)時模擬生成的150條曲線中的40條樣本曲線。

圖 1 模擬參數函數曲線

圖 2 模擬函數曲線

3.2 模擬結果

為了檢驗該方法的分類能力，在測量誤差分別為0和0.5的情況下對模型進行驗證。由于為二分類問題，根據樣本的實際標簽與分類器給出的預測標簽，可將樣本分為4種，分別為TruePositive(正類預測為正類的個數為TP)、FalseNegative(正類預測為負類的個數為FN)、FalsePositive(負類預測為正類的個數為FP)、TrueNegative(負類預測為負類的個數為TN)。根據上述定義，可對模擬生成的100個數據集給出4個分類指標，分別是精度(Acc)、準確率(Pre)、召回率(Rec)、F1得分(F1)，其計算公式分別為[7]：

同時將此方法(Bayesian Fuctional Logistic Regression,BFLR)與普通Logistic回歸(Logistic Regression,LR)、支持向量機(Support Vector Machine,SVM)、決策樹(Decision Tree,DT)、條件推斷樹(Conditonal Inference Tree,CIT)方法進行比較。

通過對比函數Logistic回歸模型與其他分類方法在模擬數據上的分類性能，發現基于BPLR模型的方法對于數據的分類情況明顯優于其他方法，在4個分類性能指標上都有更高的準確率。樣本路徑圖、樣本密度圖和樣本自相關函數圖表明，在經過預燒期后算法已趨于穩定達到收斂，證明該抽樣算法在數據分類上的有效性。

表1 模擬數據分類性能

圖 3 N=150，b的樣本路徑

圖 4 N=150，b的樣本密度圖

圖 5 N=150，b的自相關函數

4 實際數據分析

以Tecator數據為例，該數據可在R軟件包“fda.usc”[15]中進行下載。Tecator數據集由215個碎肉樣本對波長為850～1050 nm的近紅外吸收光譜曲線及其脂肪含量構成，每條吸收光譜曲線觀測了100個通道，其中有138塊碎肉樣本的脂肪含量Fat低于20%，77塊碎肉樣本的脂肪含量Fat高于20%。以此將Tecator數據集分為兩類，圖6給出了每類的各30條樣本曲線。通過函數主成分分析發現T，ecator數據集前3個主成分已經達到99%的累積方差貢獻率，因此選取前三個主成分基函數構建函數型Logistic回歸模型。該模型可以表示為：

圖 6 Tecator數據集

圖 7 各分類器ROC曲線

其中初始值α設為0.5，bk=(0,0,0),k=1,2,3，cik為前三個主成分得分。

為檢驗模型的分類能力，畫出模型的ROC曲線。結果顯示，基于貝葉斯分析的函數型Logistic回歸模型對Tecator數據集的分類效果最優，其AUC面積達到了0.984，說明模型具有較高的分類準確率。與其他方法在4個指標上的分類性能相比，盡管BFLR方法在準確率上表現不如普通Logistic回歸、決策樹和條件推斷樹，但在精度、召回率和F1得分上都顯著優于其他方法，因此總體來說與其他模型相比擁有更好的分類能力。

表2 Tecator數據集分類性能

5 結束語

本文面向函數型數據的二分類問題，提出一種基于Logit變換的函數型Logistic回歸模型，并通過模擬數據和實際數據分析驗證了其分類能力。與其他模型的分類性能相比，在該模型上的分類結果均優，但不足是本文考慮的是單變量函數型回歸變量的情形，針對多元函數型回歸變量以及包括普通數據的函數型Logistic回歸模型可為后續研究。