基于冗余信息融合的車輛質心側偏角估計方法*

夏 秋，陳 特，陳 龍，徐 興，蔡英鳳

（1. 江蘇大學汽車工程研究院，鎮江 212013；2. 滁州學院機械與電氣工程學院，滁州 239000）

前言

隨著汽車行業的蓬勃發展和相關核心技術的不斷累積，汽車產業規模逐步增大并完善，汽車的保有量與普及率也在不斷提高。汽車工業技術的不斷成熟，促進了產品競爭力的提升以及消費者對于產品的預期，使得汽車控制功能愈發完善與人性化。近年來，得益于計算機工業技術、通信技術等相關交叉領域的發展，汽車控制系統變得越來越復雜，能夠同時接收更多的傳感器信息并作出及時合理的控制決策。對于一個完整的車輛控制系統來說，準確可靠的車輛狀態信息是車輛運動規劃與動力學控制的重要支撐，車輛狀態信息的精度將直接影響到整車運動控制品質。但是，一些車輛行駛狀態，尤其是車輛質心側偏角，難以通過車載傳感器直接測量得到。因此，為降低生產和設計成本，同時考慮到當前質心側偏角傳感器缺乏的情況，很有必要設計可靠的車輛行駛狀態估計方法，通過軟測量的方式來替代實物傳感器。

目前，關于車輛行駛狀態估計方法的研究已有許多，其中，基于模型的車輛行駛狀態估計器是最為常見的一種方式。在此研究中，研究人員通常根據公認的車輛模型，并利用相應的估計算法設計車輛狀態估計器，將現有的易得的傳感器信息作為估計器輸入來計算得到所需的車輛狀態信息。目前，已有許多先進的估計理論在車輛行駛狀態觀測中得到了應用，其中包括滑模算法、神經網絡算法、粒子群算法、卡爾曼濾波算法等等。其中，卡爾曼濾波及其改進算法應用的最為廣泛，也取得了良好的估計效果。常用的卡爾曼濾波算法包括擴展卡爾曼濾波、無跡卡爾曼濾波、容積卡爾曼濾波以及粒子濾波等。隨著研究的深入，現有研究通常關注于提高改進卡爾曼濾波算法的自適應能力，從而確保該算法的多工況適應能力及其在復雜駕駛環境下的實際效果。近年來，研究者開始傾向于研究冗余輸入信息下的車輛狀態融合估計問題。根據不同車輛模型關系，設計多個車輛狀態估計器，結合多個傳感器測量信息的冗余度，利用不同估計器之間的誤差迭代與補償，來提高整個估計系統的估計精度和可靠性。

為提高車輛質心側偏角估計精度，本文中提出了一種基于冗余信息融合的車輛質心側偏角估計方法。根據車輛動力學模型和運動學模型特點，利用容積卡爾曼濾波算法分別設計了相應的車輛行駛狀態估計器，同時，在充分分析不同估計器的潛在特性和適用場景的基礎上，設計了一種車輛質心側偏角融合估計策略，采用動態自適應加權的方式提高了質心側偏角估計的精度和多工況適應能力。

1 車輛模型

為便于車輛狀態觀測器的設計并表征不同車輛參數間的數學關系，建立了橫向和橫擺方向的車輛動力學方程。車輛動力學模型如圖1 所示，建立了動態坐標系，其中，動態坐標系原點與車輛質心重合，軸為車輛縱向行駛方向，軸為車輛橫向運動方向。本文不考慮車輛懸架系統的動力學方程，只討論了車輛在平面上的運動，忽略了車輛俯仰、橫擺、垂向運動。單軌車輛模型的動力學方程可以表示為

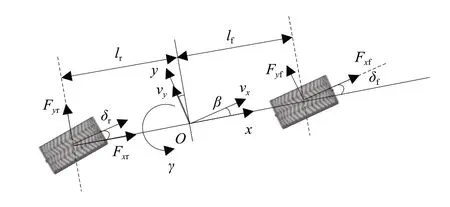
圖1 單軌車輛模型

式中：v為縱向車速；v為側向車速；為橫擺角速度；為汽車質量；I為繞軸的轉動慣量；和分別為車輛質心距前、后軸的距離；F和F分別為前、后輪胎的橫向輪胎力。

式中：和分別為前、后輪胎的輪胎側偏剛度；和分別為前、后輪胎的輪胎側偏角。

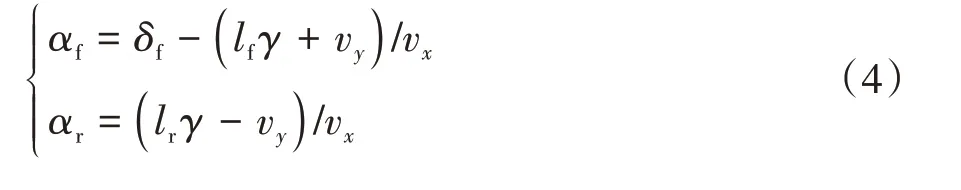
式中為車輛前輪轉角。車輛質心側偏角可表示為

聯立式（1）、式（2）和式（5），可得單軌車輛動力學模型為

縱向車速的運動學方程可以表示為

式中a為車輛縱向加速度。橫向車速的運動學方程可表示為

式中a為車輛橫向加速度。四輪轉速的運動方程可表示為

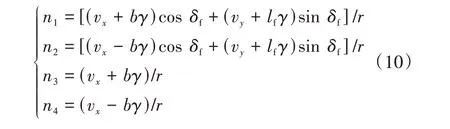
式中：、、、分別為左前輪、右前輪、右后輪、左后輪的輪速；為半輪距；為車輪有效半徑。從而，利用式（10）便可建立四輪轉速與縱向車速、橫向車速和車輛橫擺角速度之間的關系。

2 車輛質心側偏角融合估計方法

2.1 用于車輛狀態估計的容積卡爾曼濾波

式（6）、式（7）中的車輛動力學模型和式（8）、式（9）中的車輛運動學模型皆可用于車輛狀態估計，且其皆可表示為如下的離散狀態空間方程：

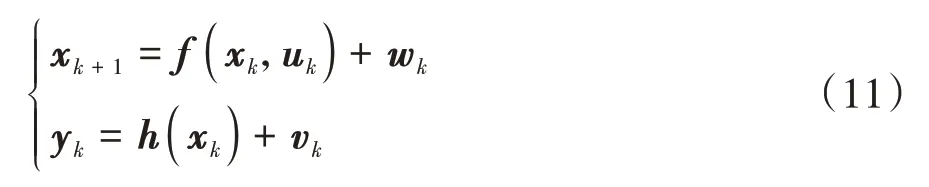
式中：x為離散系統狀態向量；y為離散系統測量向量；（·）為離散系統狀態轉移方程；（·）為離散系統測量方程；w為系統噪聲；v為測量噪聲，w和v為互不相關的高斯白噪聲。

與普通擴展卡爾曼濾波相比，容積卡爾曼濾波能有效地減小濾波發散，且其計算量僅與待估系統的狀態維數成正比，因此能有效減小計算量，近年來在許多領域得到了廣泛的應用。根據式（11）中的非線性狀態空間方程，自適應容積卡爾曼濾波算法的迭代步驟如下。

（1）選擇初始值

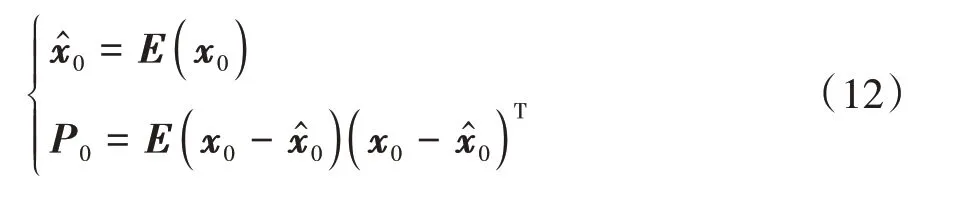
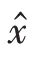
（2）計算容積點

式中：為容積點序列號；n為系統模型維數；可通過對P計算Cholesky 分解得到S且有P= SS；ξ=n[1] 為容積點。從而，分別對應車輛動力學模型估計方法和運動學模型估計方法的容積點可表示為

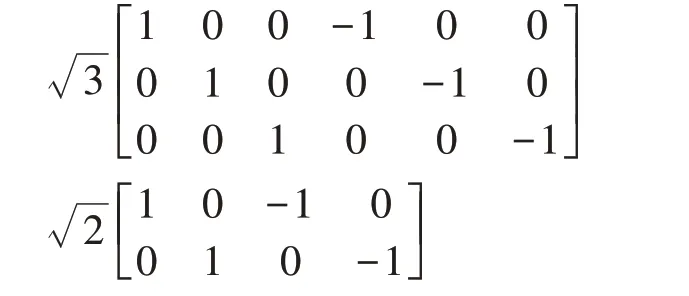
（3）時間更新

容積點傳播可表示為

一步狀態預測方程可表示為

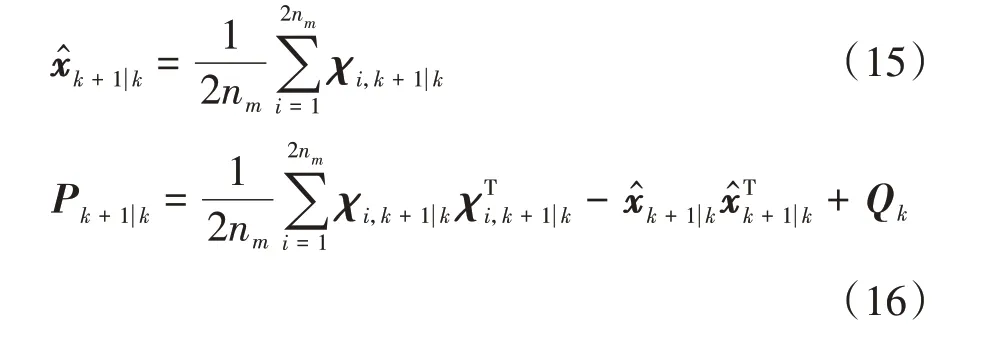
式中Q為w的協方差矩陣。

（4）測量更新

P的Cholesky分解可表示為

容積點可表示為

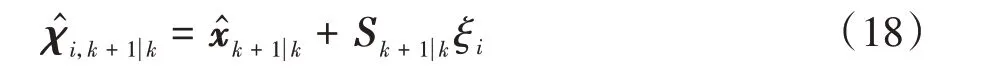
容積點傳播可表示為

測量更新預測結果可表示為

測量預測結果的協方差矩陣和互協方差矩陣可分別表示為

式中R為v的協方差矩陣。ε的預測誤差可通過計算實際測量值和預測測量值之間的差值獲得。

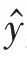
車輛狀態估計值為

車輛狀態估計的誤差協方差矩陣可表示為

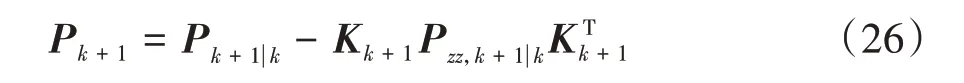
2.2 基于動力學模型的車輛質心側偏角估計

根據車輛動力學模型和容積卡爾曼濾波算法，設計基于動力學模型的車輛質心側偏角估計器。由式（5）和式（8）可得

從而，式（6）、式（7）和式（29）的離散化結果可以表示為

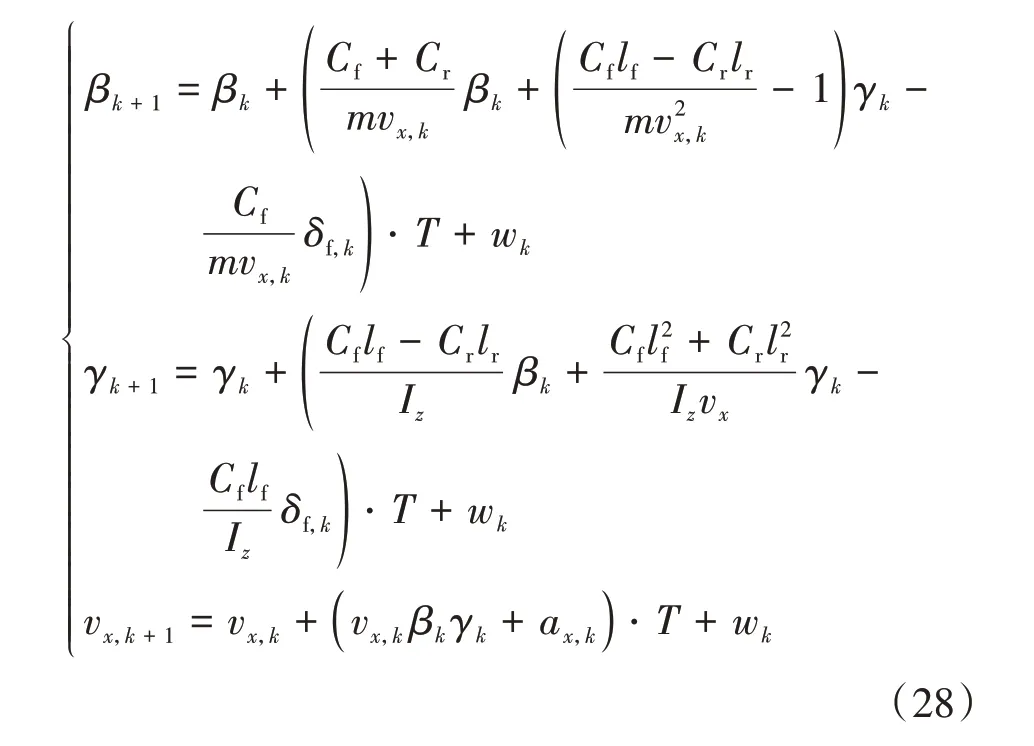
式中為卡爾曼濾波的采樣周期。根據式（5）、式（6）和式（9），可得

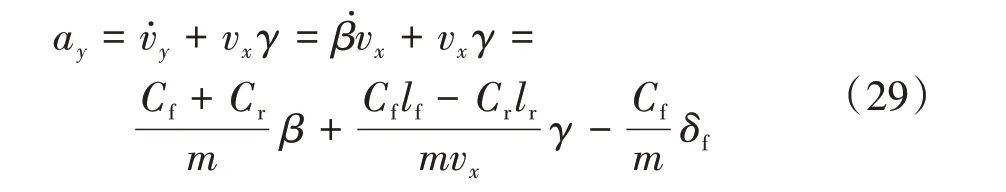
從而，式（29）可用作動力學模型估計器的測量更新方程，且其離散化形式可表示為

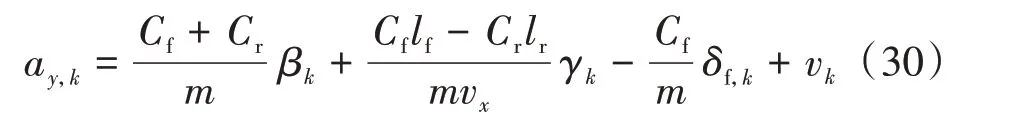
從而車輛動力學系統模型的Jacobi矩陣可表示為

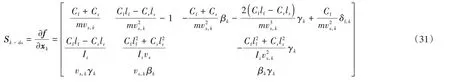
從而，動力學模型估計器的測量矩陣可表示為

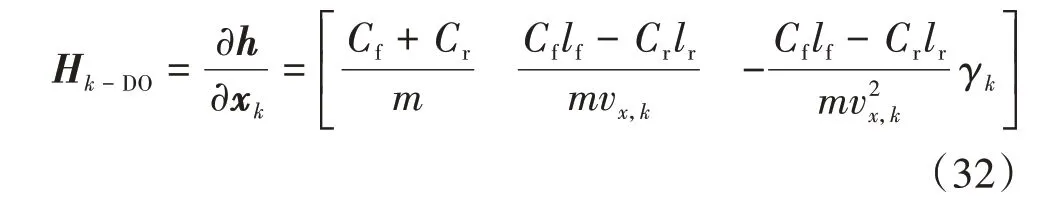
根據車輛動力學模型的離散方程，可采用如前所述的容積卡爾曼濾波算法來設計車輛狀態估計器，其中卡爾曼濾波的狀態向量為x=[β γ v]， 測 量 向 量 為y=[a]，已知輸入為u=[ a]。

2.3 基于運動學模型的車輛質心側偏角估計

然而，基于動力學模型的車輛狀態估計器只考慮了線性輪胎模型的情況，當輪胎力處于非線性區域時，估計精度會出現一定程度的下降。同時，當測量得到的車輛橫向加速度出現未知偏差時，容易造成估計誤差自循環和誤差累積，使得基于動力學模型的卡爾曼濾波估計結果偏離實際值。為了避免這一問題，利用車輛運動學模型設計車輛行駛狀態估計器，旨在利用車輛測量信息的冗余度，提高估計結果的精度和自適應能力。同樣地，式（8）和式（9）的離散化方程可表示為

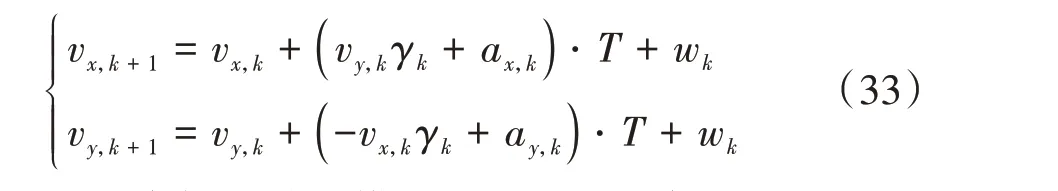
從而車輛運動學模型的Jacobi矩陣可表示為

然后，根據式（10）中的四輪轉速方程，設計運動學模型估計器的測量更新方程。從而，可利用測量信息的冗余度來提高估計結果可靠性。式（10）的離散化結果可寫成

根據式（32），運動學模型估計器的測量更新矩陣可表示為

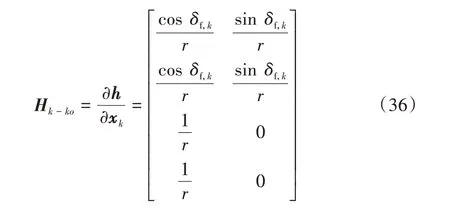
從而，利用如前所述的容積卡爾曼濾波算法，可設計基于運動模型的車輛狀態濾波器，實現對縱向車速和橫向車速的估計，其中，卡爾曼濾波的狀態向量 為x=[v v]，測 量 向 量 為y=[ n n n]， 已 知 輸 入 為 u=[ γ a a]。然后，利用式（5）并結合估計所得的縱向車速和橫向車速，即可得到基于運動學模型的車輛質心側偏角估計結果。

2.4 車輛質心側偏角融合估計策略

在基于動力學模型的濾波器設計過程中，輪胎側向力的計算公式是線性的。結合輪胎側向力和輪胎側偏角之間的關系可知，當輪胎側偏角較小時，輪胎側向力與輪胎側偏角間呈線性關系，當輪胎側偏角過大時，輪胎側向力達到飽和并隨著輪胎側偏角的增大而略微減小。也就是說，當輪胎側向力處于線性區域時，基于動力學模型的濾波器具有較高的估計精度。然而，當輪胎側偏角過大時，輪胎受力會達到非線性區域，此時車輛模型的不確定性會降低基于動力學模型濾波器的估計效果。

基于運動學模型的濾波器具有良好的穩態估計性能，故其估計能力不受輪胎側向力飽和現象的影響。然而，當輪胎受力處于線性區域時，基于輪速信息的估計方法的精度比基于動力學模型的估計方法要低。特別是當車輛輪胎力的動態響應速度較快時，由輪胎力變化產生的輪速信息變化會有一定程度的滯后，導致輪速信息不足以及時反饋車輛動態關系的變化。當輪胎力處于非線性區域時，輪胎側向力的動態變化速度減慢，使得單位幅值的輪胎力增減引起的車輪轉速變化范圍相對較小，說明基于運動學模型的濾波器在該情況下具有更好的估計效果。

根據以上分析，結合兩種估計器的優點和適用場景，如圖2 所示，提出了一種新的車輛質心側偏角融合估計策略。

圖2 融合估計策略

在圖2 中，基于車輛動力學模型的狀態估計器所得的縱向車速、橫擺角速度和質心側偏角分別表示為v、和，基于車輛運動學模型的狀態估計器所得的縱向車速、側向車速和質心側偏角分別表示為v、v和。為了避免模型不確定性和未知干擾對估計效果的影響，采用誤差補償的方式來提高車輛狀態估計精度，補償結果可表示為

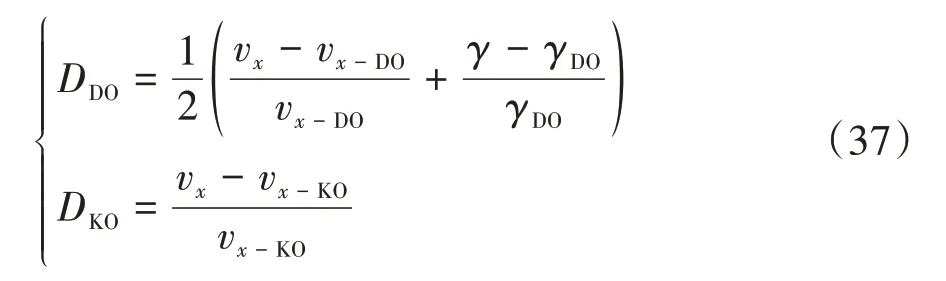
式中和分別表示動力學模型估計器和運動學模型估計器的偏差度。從而，車輛質心側偏角估計的補償結果可表示為

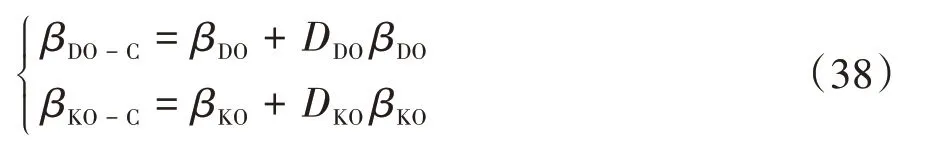
式中和分別為動力學模型估計器和運動學模型估計器補償后的車輛質心側偏角。

由圖2 可知，輪胎側偏角影響動力學模型估計器和運動學模型估計器的適用場景。為融合動力學模型估計器和運動學模型估計器的補償結果，設計了自適應權重計算模塊，依據輪胎側偏角來動態調整不同估計器間的權重系數。根據式（4）可得

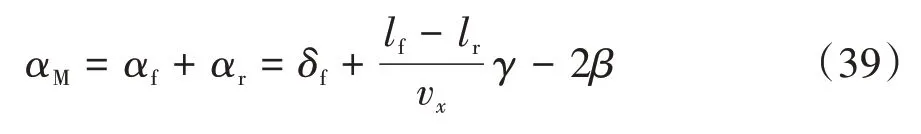
式中為標稱輪胎側偏角。因此，自適應權重系數可設計為

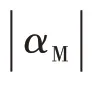
此外，調節參數和的取值也影響和增加和減小的變化速度。如果和的取值過小，則自適應權重系數對輪胎側偏角的變化將會十分敏感，其動態調節能力和多工況自適應能力將會大大下降。如果和的取值過大，則權重系數的調節范圍和動態響應能力將會下降。測試可知，當調節參數的取值分別為2.25 和5 時，融合估計效果相對較好。根據自適應權重系數，可得車輛質心側偏角的融合估計結果為

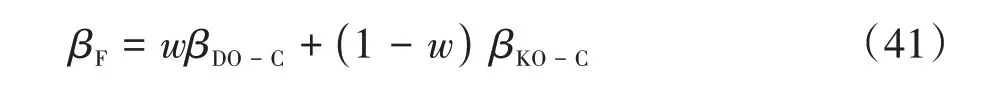
式中為質心側偏角融合估計值。同時，所得的質心側偏角融合估計值被用作自適應權重計算模塊的輸入量。

3 仿真驗證

為了驗證文中提出的車輛質心側偏角融合估計策略的應用效果，利用Carsim-Simulink 聯合仿真平臺進行了仿真驗證，對應的車輛參數如表1所示。

表1 車輛參數

3.1 正弦轉向工況

首先進行了正弦轉向工況下的車輛仿真驗證，仿真中所設置的轉向盤轉角如圖3 所示。分別進行了低速和高速兩種情況下的仿真測試，對應車速分別為36 和72 km/h。低速正弦轉向工況下的狀態估計仿真結果如圖4 所示。該工況下車輛轉向運動相對較為平緩，故基于動力學模型的狀態估計器的估計效果略好于基于運動學模型的狀態估計器，同時，自適應權重系數能夠隨著車輛行駛狀態的變化而動態調整，從而確保融合估計結果更好地跟蹤實際的車輛質心側偏角，提高了整體估計精度。圖5 所示為高速正弦轉向工況下的車輛狀態估計結果，可知動力學模型估計器和運動學模型估計器都能保持良好的觀測效果且動力學模型估計器效果略好，而融合估計結果能動態調整兩種估計器間的權重系數，從而進一步提高估計效果。

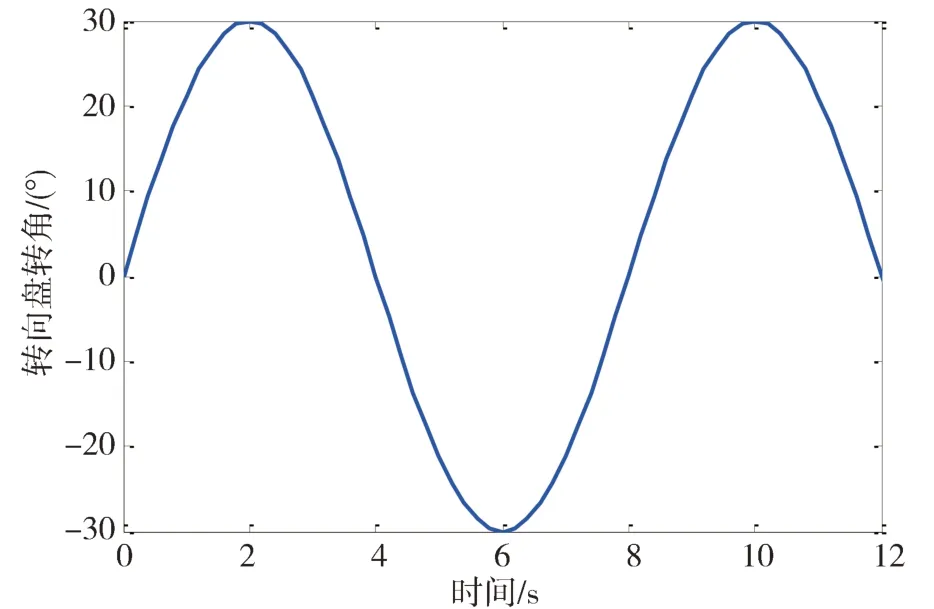
圖3 正弦轉向工況轉向盤轉角

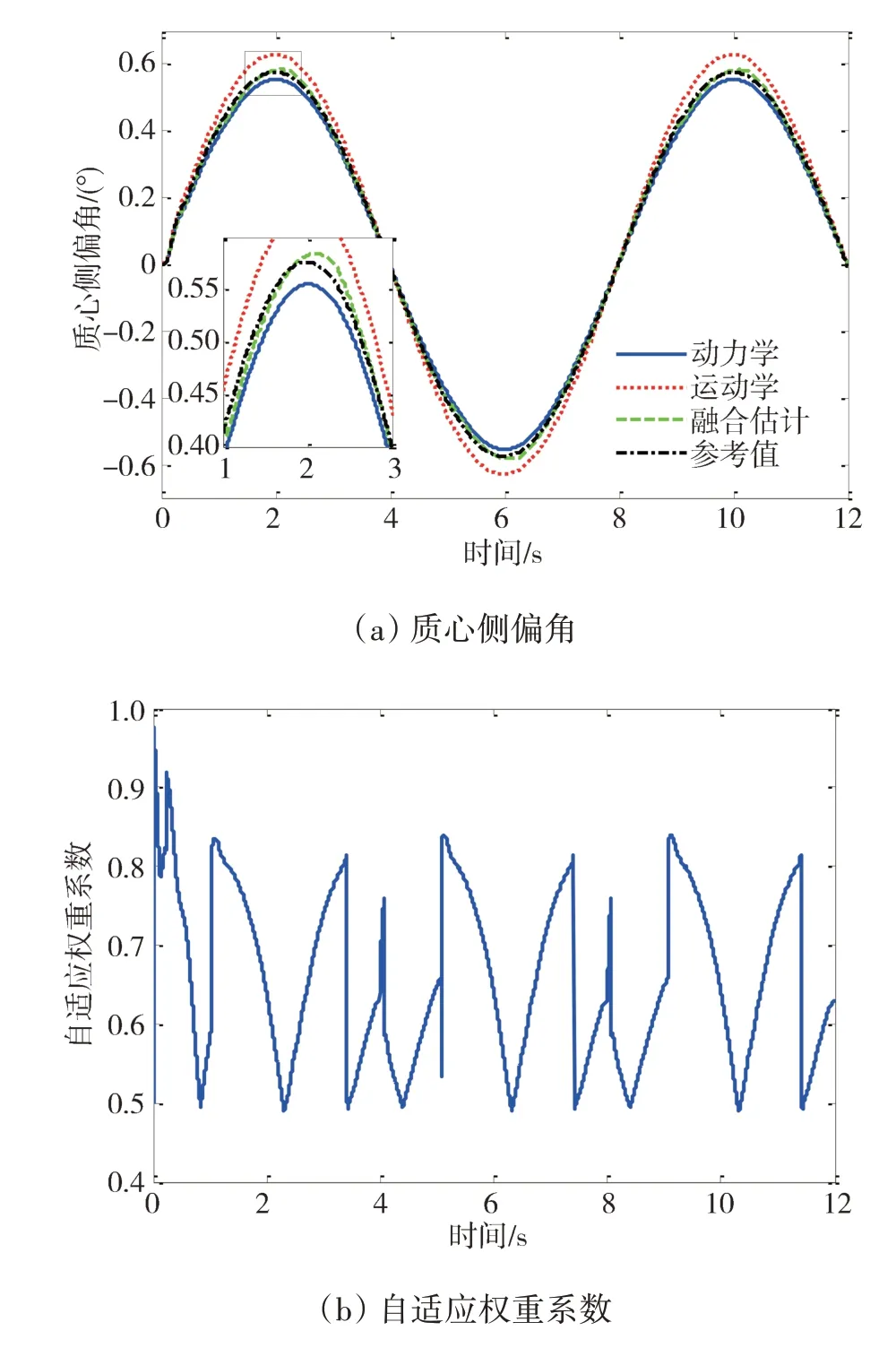
圖4 低速正弦轉向工況估計結果

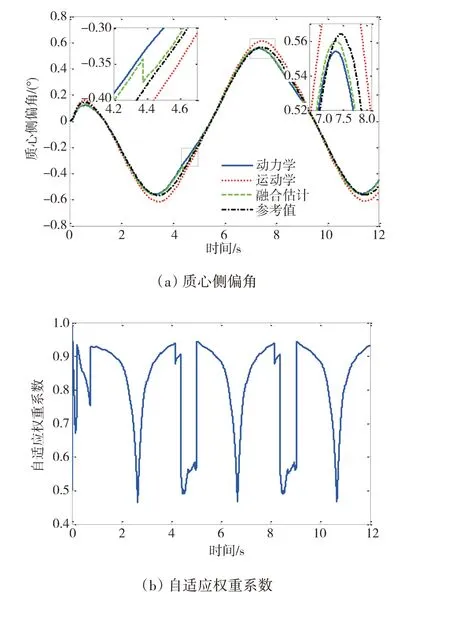
圖5 高速正弦轉向工況估計結果

3.2 魚鉤轉向工況

為了進一步體現文中方法的效果，進行了轉向操縱更為劇烈的魚鉤轉向工況下的車輛仿真驗證，仿真中所設置的轉向盤轉角如圖6所示。

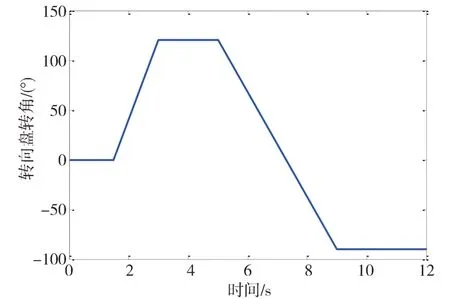
圖6 魚鉤轉向工況轉向盤轉角

首先進行了定車速魚鉤轉向工況下的聯合仿真測試，仿真中車速設定為90 km/h，所得的車輛狀態估計結果如圖7 所示。由于魚鉤轉向工況下的轉向盤轉角及其變化率相對正弦轉向工況來說都更加劇烈，故此時車輛的質心側偏狀況也相對較大。從而，魚鉤轉向工況下，基于動力學模型的狀態估計器的觀測效果相對來說有所下降，而基于運動學模型的估計器此時效果更優。因此，該工況下的自適應權重系數相對較小，提高了運動學模型估計器在融合估計結果中所占的權重，從而可有效確保融合估計結果的估計精度。同時，由于車輛質心側偏角的大小與輪胎側偏角的大小直接相關，觀察可知，在車輛質心側偏角數值增大時，自適應權重系數傾向于被控制在一個較小的數值來提升估計精度，從而反映了融合估計方法的動態調節能力。

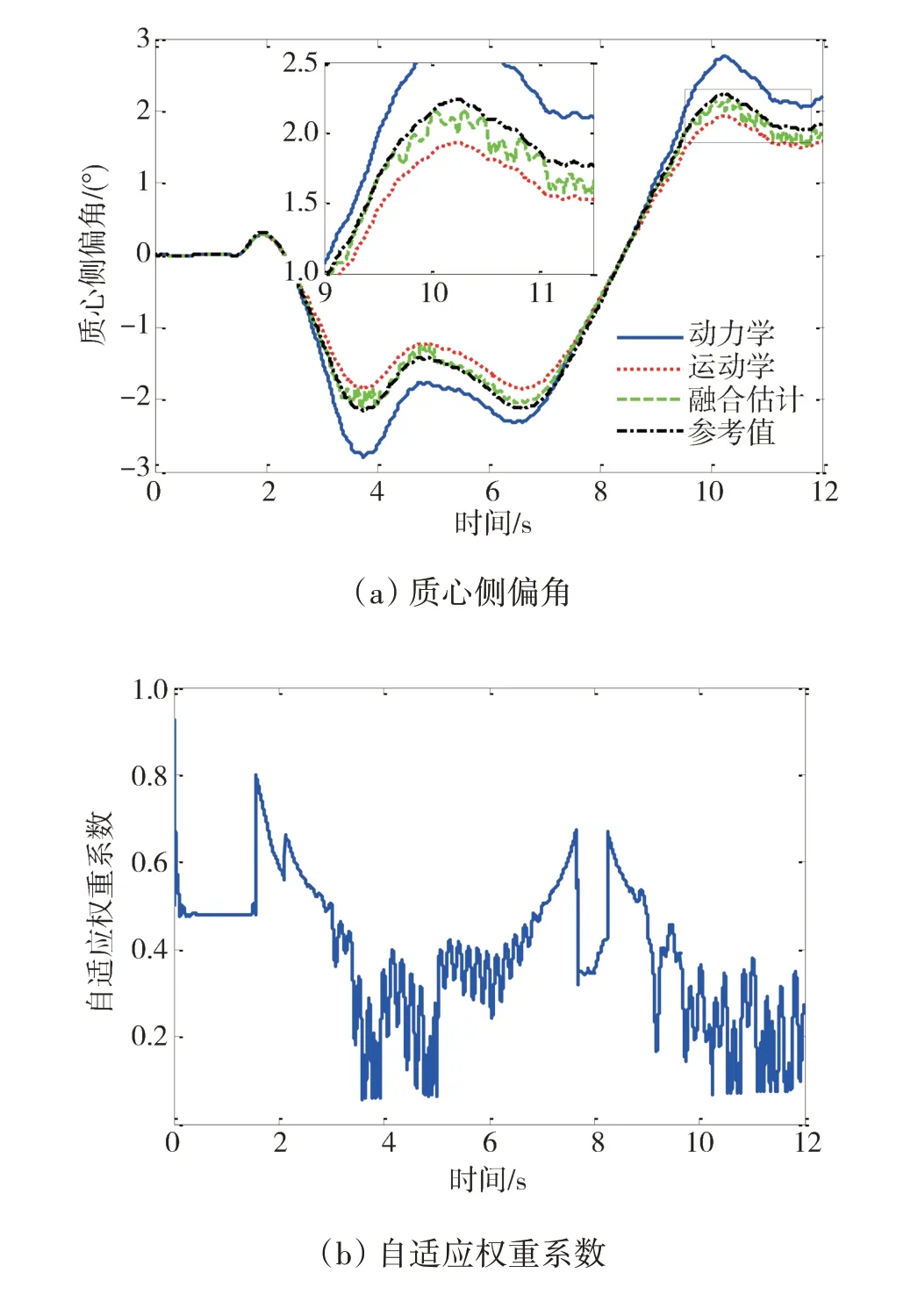
圖7 定速魚鉤轉向工況估計結果

此外，進行了變車速魚鉤工況下的車輛仿真測試，仿真中對應的車速變化情況如圖8 所示，所得的車輛狀態估計結果如圖9所示。

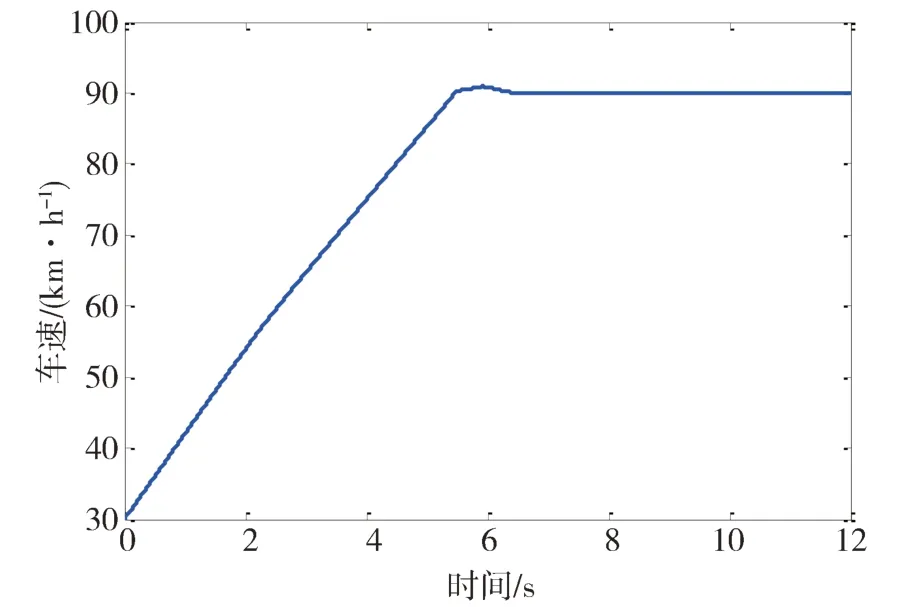
圖8 車速變化情況

圖9 變速魚鉤轉向工況估計結果

同樣地，由于轉向盤轉角和車速的劇烈變化，該工況下車輛質心側偏角的幅值和波動變化也相對較大，同時，由于該工況下動力學模型估計器的估計效果有所下降，故此時自適應權重系數相對偏小，使得融合估計結果中運動學模型估計器所占比重增加，從而確保整體估計效果。通過對比正弦轉向工況和魚鉤轉向工況下的自適應權重系數可知，車輛起步初期，融合估計結果中傾向于對動力學模型估計器匹配較大的權重系數。這是由于車輛起步初期輪胎模型大多處于線性區域，且動力學模型估計器的動態響應能力相對更快。

4 試驗驗證

為進一步驗證融合估計策略在車輛實際應用中的效果，進行了實車道路測試。實車道路測試條件如圖10 所示。試驗時，利用安裝于4 個車輪處的輪速傳感器采集四輪轉速，利用GPS/INS 慣導系統采集車身姿態，前輪轉角由轉向盤轉角傳感器測量值轉化得到，采用Vehicle SPY 對試驗數據進行記錄并保存于筆記本電腦。實車試驗采集得到的車輛狀態如圖11 所示，試驗驗證結果如圖12 所示。由圖12可知，在實車應用中，基于動力學模型和基于運動學模型的車輛狀態估計方法都能整體跟蹤實際車輛行駛狀態，同時，根據局部放大圖可知，采用融合估計方式所得的車輛質心側偏角具有更高的估計精度。此外，自適應權重系數能夠隨著車輛行駛狀態的變化而動態調整，反映了融合估計方法的自適應調節能力。由于實際道路測試中的車速和轉向盤轉角與仿真工況對比都相對較小，故整體上來說自適應權重系數基本在0.6～0.9 之間變化，也就是說，在融合估計結果中基于動力學模型的質心側偏角估計結果占有更大的比重。該分配趨勢與理論設計和仿真結果中的權重分配方式相吻合，從而進一步驗證所提出的融合估計方法在實車應用中的效果。

圖10 實車道路試驗

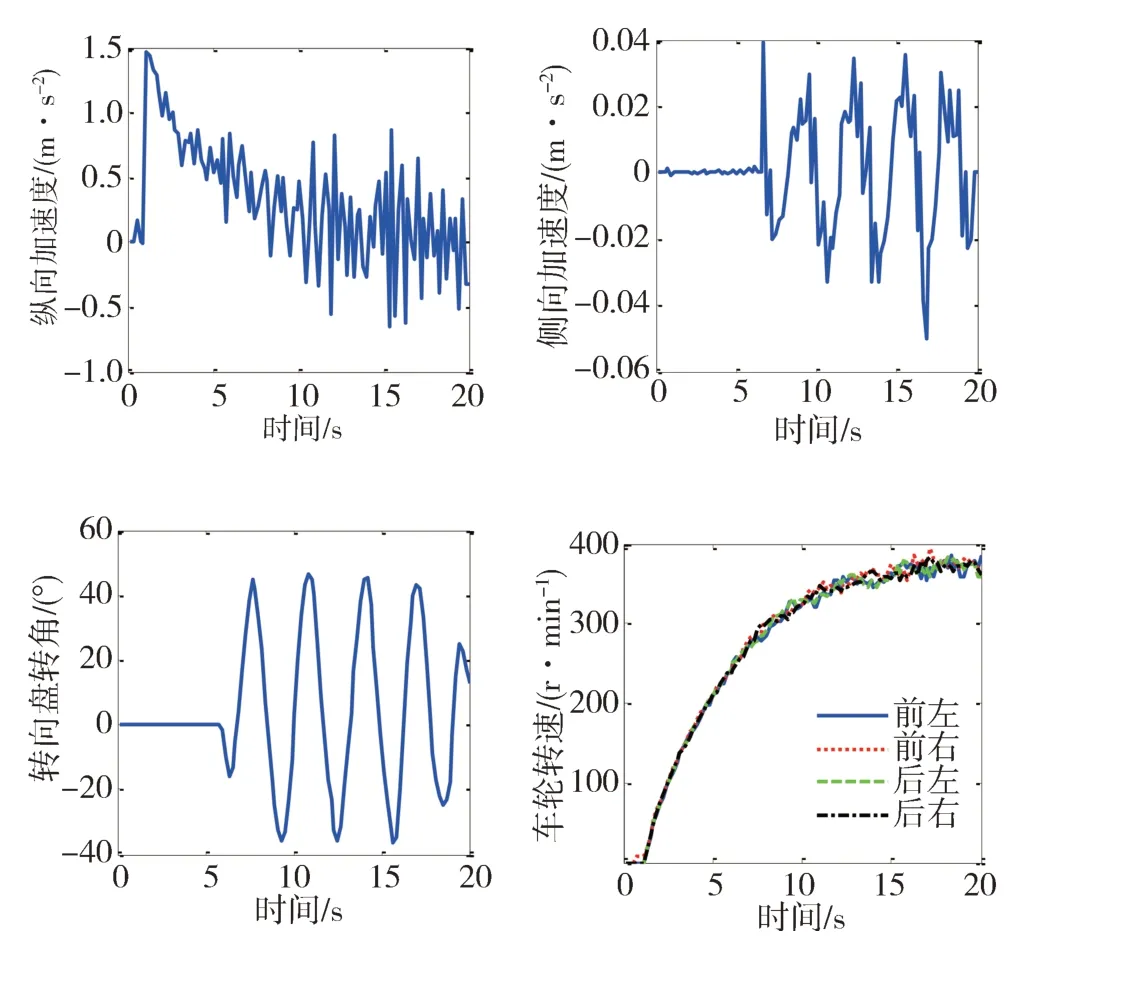
圖11 實車道路試驗車輛狀態

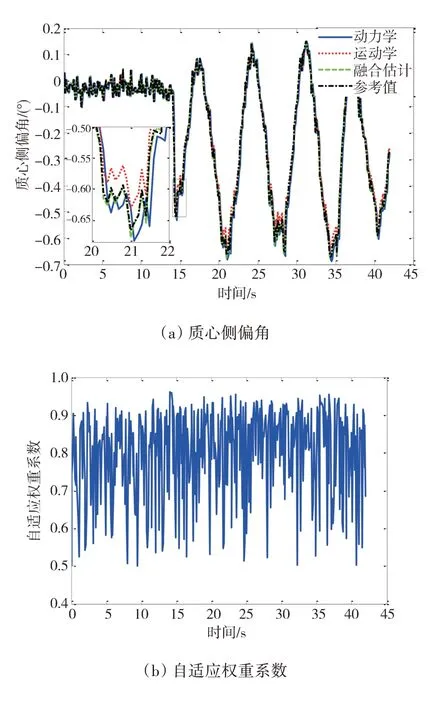
圖12 實車道路試驗估計結果

5 結論

（1）基于動力學模型的車輛狀態估計器和基于運動學模型的車輛狀態估計器適用于不同的車輛行駛狀態。當輪胎側偏角較大時，運動學模型估計器的估計精度相對較高，當輪胎側偏角相對較小時，動力學模型估計器的估計精度相對較高。

（2）所設計的車輛質心側偏角融合估計策略能夠根據車輛行駛狀態的變化而動態調節動力學模型估計器和運動學模型估計器之間的權重系數，從而提高融合估計效果。

（3）所提出的融合估計方法在正弦轉向工況和魚鉤轉向工況的仿真測試和實車道路測試中都能保持良好的估計效果，整體估計精度相比單獨的動力學模型估計器和運動學模型估計器都得到了提升。