線性EIV模型參數的LASSO估計方法
趙明清,席甜甜
(山東科技大學 數學與系統科學學院,山東 青島 266590)
針對線性EIV模型參數的最優估計問題,國內外學者對其進行了廣泛而深入的研究,先后提出了整體最小二乘(TLS)法和加權整體最小二乘(WTLS)法,并在此基礎上進行了拓展性研究[1-10]。但以上研究只考慮了模型的擬合優度,而忽略了其復雜度,這易導致過擬合現象,并因此會降低模型的泛化能力。為此,王樂洋等[11]在WTLS的基礎上添加參數向量的2-范數懲罰項,并做某種近似處理后得到了參數估計的解析解;Zhu等[12]在LS的基礎上添加隨機誤差矩陣的F-范數和參數向量的1-范數懲罰項,將單層優化問題轉化為雙層優化問題進行求解,給出了具體的參數估計數值解算法,并在WTLS的基礎上添加參數向量的1-范數懲罰項,采用類似的技巧進行了討論,但沒有給出其具體求解算法。本文基于結構風險最小化原則,提出線性EIV模型參數的LASSO估計(LE)方法,通過運用該方法對2001—2017年我國個人衛生支出占比影響因素的實證,與WTLS、LS兩種方法進行對比分析,以說明LE方法的有效性。
本文所有數據處理均使用Python語言。
1 線性EIV模型參數的LASSO估計
線性EIV模型的矩陣形式為[7-10,13]
y-ey=(A-EA)β,
(1)
式中:y=(y1,y2,…,yn)T表示被解釋變量觀測值;ey=(e1,e2,…,en)T表示y的隨機誤差;A=(aij)n×(m+1)表示解釋變量觀測值矩陣;EA=(eij)n×(m+1)表示A的隨機誤差矩陣;β=(β0,β1,…,βm)T表示未知參數向量;eA=vec(EA)是將EA按列向量化后得到的列向量;隨機誤差向量

(2)
記
Q0=P-10,Q1=P-11,
(3)
式中:?表示矩陣的Kronecker積[14];Py為y的權陣;PA為A的權陣;P0為A的列向量權陣;P1為A的行向量權陣。關于偽逆陣的求解見文獻[15]。
文獻[7]給出了該模型的WTLS數值解迭代算法。本文基于結構風險最小化原則[16],借鑒LASSO回歸思想[17],在所有數據加權殘差平方和(反映擬合優度)的基礎上加上一個1-范數懲罰項(反映復雜度),即為線性EIV模型參數的LASSO估計(LE)方法,模型如下:
(4)
式中μ≥0為懲罰參數。令
Φ(ey,eA,λ,β)=
2λT(y-ey-(A-EA)β)=
2λT(y-Aβ-ey+(βT?In)eA),
(5)
又令
(6)
(7)
(8)
(9)
在式(9)中
r=(r0,r1,…,rj,…,rm),
(10)
由式(6)、式(7),得
ey=Qyλ,
(11)
eA=-(Q0?Q1)(β?In)λ=
-(Q0β?Q1)λ。
(12)
根據恒等式[7]
vec(HFGT)=(G?H)vec(F),
(13)
并由式(12),得
EA=-Q1λ(Q0β)T=-Q1λβTQ0。
(14)
將式(11)、式(12)代入式(8),得
y-Aβ=ey-(βT?In)eA=
Qyλ+(βTQ0β?Q1)λ,
(15)
因此,有
λ=(Qy+(βTQ0β)Q1)-1(y-Aβ)。
(16)
將式(16)分別代入式(11)、式(14),得
ey=Qy(Qy+(βTQ0β)Q1)-1(y-Aβ),
(17)
EA=-Q1(Qy+(βTQ0β)Q1)-1(y-Aβ)βTQ0。
(18)
將式(16)、式(18)代入式(9),得
(19)
式中:
v=(y-Aβ)T(Qy+(βTQ0β)Q1)-1Q1·
(Qy+(βTQ0β)Q1)-1(y-Aβ)。
(20)
由式(19),得
β=(2AT(Qy+(βTQ0β)Q1)-1A-2vQ0)-1·
(2AT(Qy+(βTQ0β)Q1)-1y-μr),
(21)
式(21)是優化問題(4)的最優解所滿足的條件方程。令
U=2AT(Qy+(βTQ0β)Q1)-1A-2vQ0,
(22)
V=ββT,
(23)
W=2VAT(Qy+(βTQ0β)Q1)-1,
(24)
則式(21)可寫為
VUβ-Wy=-μVr,
(25)
考慮式(25)等號兩邊的第j個分量,有
(VUβ-Wy)j=-(μVr)j,j=0,1,…,m。
(26)
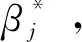
由以上分析,可以給出LE方法數值解的求解算法如下:
(1)取初始值v(0)=0,β(0)=N-1C,[N,C]=ATPy[A,y],i=0,并給定迭代誤差允許范圍ε。
(2)計算第i+1次迭代β(i+1):
①j=0
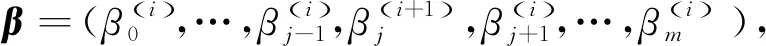
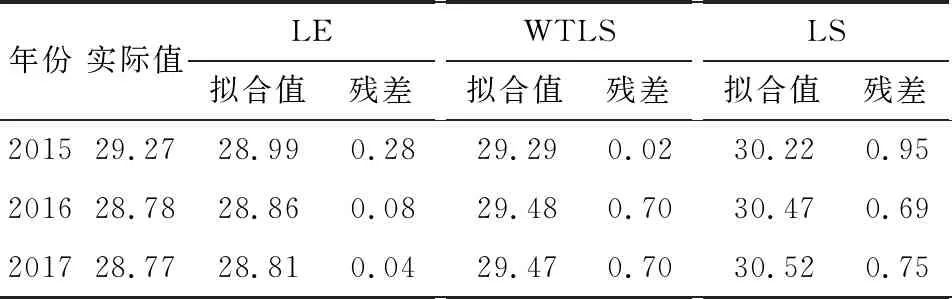
③如果intercept>yA,則rj=-1,否則如果intercept ⑤j=j+1 ⑥如果j≤m,則轉② (4)i=i+1,轉(2)。 (5)結束。 在實際應用時,算法中的權陣通常賦予特殊形式[7]。 本文利用LE方法對2001—2017年我國個人衛生支出占比(y)的影響因素進行分析,并與WTLS、LS兩種方法進行比較,以進一步驗證本方法的有效性。 我國個人衛生支出占比的影響因素很多,根據相關文獻[19],本文從衛生總費用、人口、政策、經濟、醫療技術水平、醫療服務供給收入6個觀察點選取了12個指標作為影響我國個人衛生支出占比的因素,詳見表1。 表1 個人衛生支出占比影響因素 本文所用的個人衛生支出占比及其各影響因素指標數據均來源于中國統計年鑒以及中國衛生統計年鑒。其中,2001—2014年的14組數據作為訓練數據集,2015—2017年的3組數據作為測試數據集。 2.3.1 多重共線性診斷 本文對上述12個解釋變量做多重共線性診斷,結果見表2。由表2可以看出:9—13維度的特征值約等于0,并且其條件索引的值遠大于10,說明解釋變量間存在較嚴重的多重共線性。 表2 多重共線性診斷 2.3.2 基于LE方法的建模 為計算方便,本文對權陣進行了一定的簡化,即令 P0=diag(0,1,1,1,1,1,1,1,1,1,1,1,1), P1=I14,Py=I14。 給定ε=0.5×10-8,通過K-折交叉驗證法[17](這里K=10)選取懲罰參數μ=0.002 6,參數估計結果為 0.123 0X4+0.000 2X7-0.036 2X8。 (27) 由此可知,12個指標中7個指標的系數已壓縮為0,其影響被完全忽略,僅留下5個指標,還可以看出:政府衛生支出占衛生總費用比例、社會衛生支出占衛生總費用比例、城鎮人口比和嬰兒死亡率對個人衛生支出占比都呈現負向影響;人均GDP對個人衛生支出占比呈現正向影響。 2.3.3 對比分析 本文分別采用WTLS、LS兩種方法對回歸模型參數進行估計,其結果為: 1.598 1X3-0.273 4X4-0.492 4X5- 0.086 0X6-0.000 3X7-0.009 1X8- 2.327 5X9+0.504 3X10+0.000 7X11+0.000 1X12, (28) 1.548 9X3-0.261 4X4-0.466 5X5- 0.091 4X6-0.000 3X7-0.007 2X8- 2.327 5X9+0.519 2X10+0.000 7X11+0.000 1X12。 (29) 可以看出,在WTLS和LS兩種方法中,政府衛生支出占衛生總費用比例、社會衛生支出占衛生總費用比例、城鎮人口比、失業率、衛生總費用占GDP比例、人均GDP、嬰兒死亡率和每千人口床位數對個人衛生支出占比都呈現負向影響;65歲及以上老年人口比、每千人口醫生數、城鎮人均純收入和農村人均純收入對個人衛生支出占比都呈現正向影響。 但是,WTLS和LS兩種方法的估計都存在系數正負號不符合實際的狀況,如人均GDP的系數為負,這與實際情況不符。因為隨著人均GDP的增長,生活水平越來越好,人們更加注重身體健康,從而會促進個人衛生支出占比。該結果可能是由解釋變量間多重共線性的影響造成的。 根據上述三種估計方法所求的回歸方程對測試數據集進行預測,并與實際數據進行對比,結果見表3。顯然,LE方法得到的預測值更準確。 表3 個人衛生支出占比預測值與實際值對比 將本文提出的LE方法與WTLS、LS兩種方法進行對比分析,結論如下: 1)LE方法全部系數正負號都符合實際,但在WTLS與LS兩種方法中,部分系數正負號不符合實際。 2)LE方法預測精度更高。LE、WTLS和LS相對于實際值的均方根誤差分別為0.169 7、0.571 7、0.806 6,可見LE方法的精度更高。 3)LE方法的擬合優度更高。各方法的決定系數R2如下:WTLS的為0.990 4、LS的為0.960 5、LE的為0.999 1,可見LE的擬合效果更好。 本文提出了基于結構風險最小化原則的線性EIV模型參數的LE方法,并給出了其數值解的快速迭代算法。如果直接由條件方程設計求解算法,那么算法的效率不高,為此本文做了技術上的處理。另外,算法還考慮到了解的唯一性問題。為了說明該方法的有效性,本文結合實證與WTLS、LS兩種方法進行了對比分析,結果表明: LE方法能夠進行高維回歸系數壓縮,實現降維的目的,明顯提高預測精度,具有更強的泛化能力,達到更高的擬合優度。這樣的結果和文獻[20]相比更理想。本文的研究還需要進一步完善,如可以針對參數估計的統計性質進行深入探討等。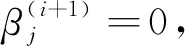
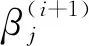
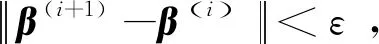
2 模型比較
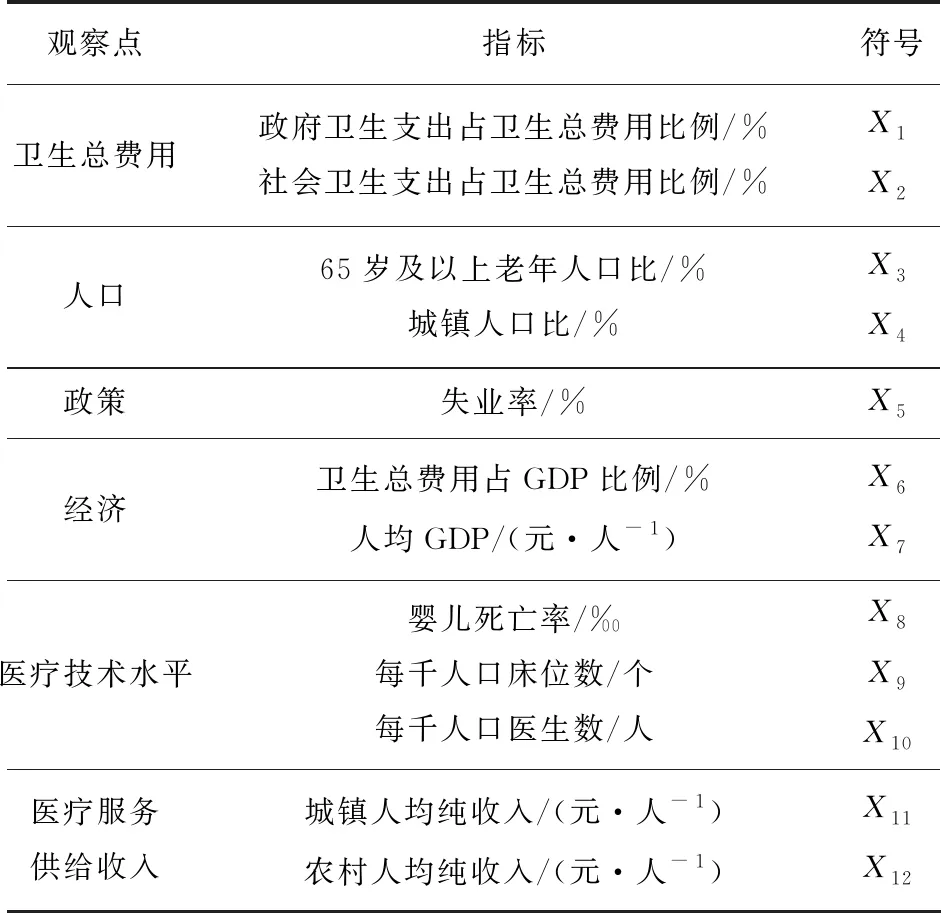
2.1 指標體系構建
2.2 數據獲取
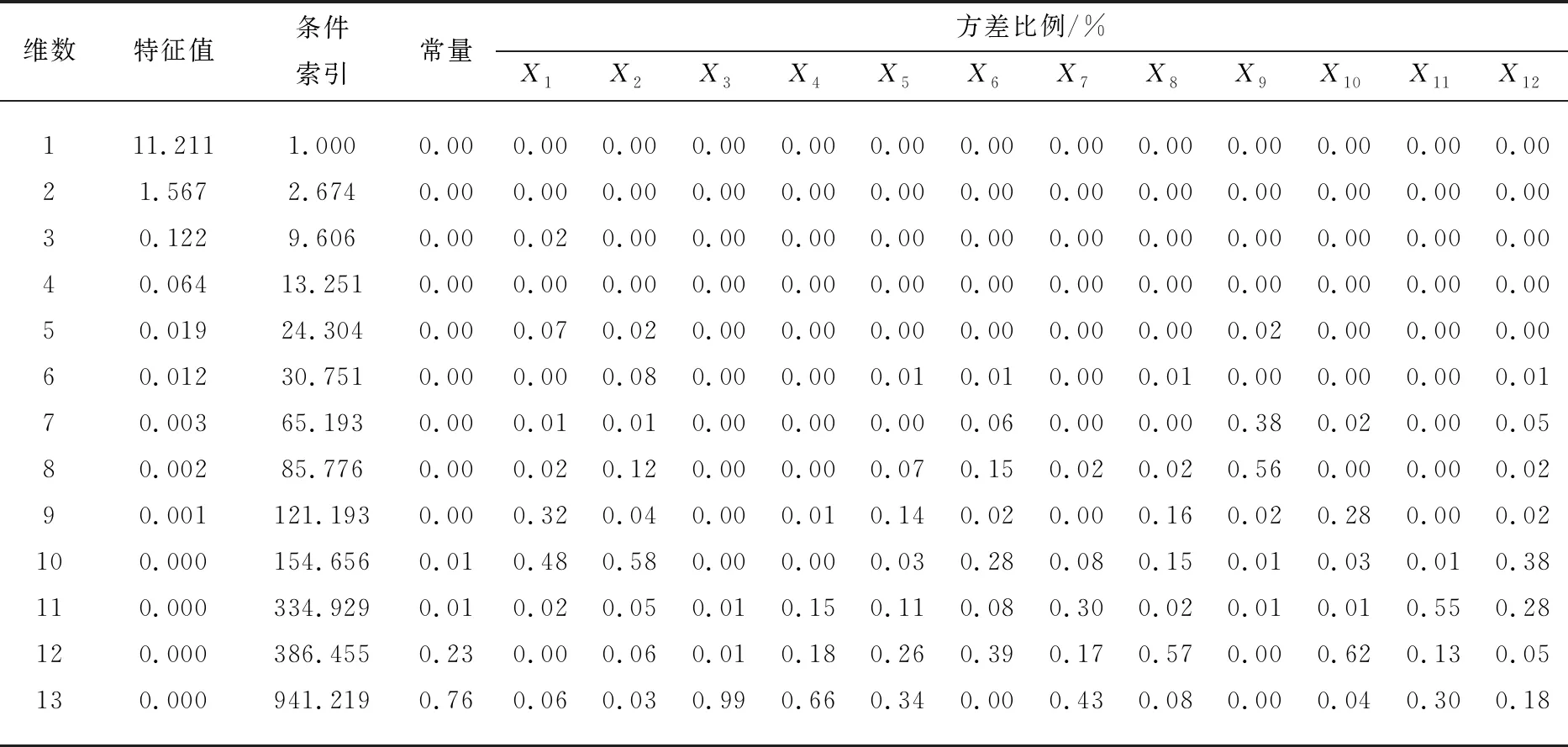
2.3 模型建立與對比分析
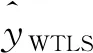
3 結束語

