混合灰色預測模型HGM(1,1)

適越通，秦華，白成昊，劉子祥

(山東理工大學 物理與光電工程學院，山東 淄博 255049)

灰色理論首先由鄧聚龍教授[1]提出，國際上給予了很高的評價。灰色系統為部分清楚、部分未知的數據信息[2-5]，此理論認為盡管信息復雜、朦朧，但有一定的發展趨勢和整體功能。本文研究分析了GM(1,1)[1]、基于緩沖算子和時間響應函數優化的GM(1,1)[2]、VWGM、FGM(1,1)[3]等理論有關的諸多模型，發現它們存在的不足之處，并采用FGM(1,1)和VWGM的混合模型即HGM(1,1)對數據處理。混合的模型不僅將變權緩沖算子引入灰色模型，并且基于灰色關聯分析和粒子群優化算法確定模型最優參數，不僅解決傳統緩沖算子作用強度不可調的問題[6]，還可能實現對原始數據的動態預處理，改善模型預測精度，保證預測結果盡可能地保持原有序列的內在趨勢以及變化規律，提高模型擬合和預測的穩定性和綜合性能。

1 傳統GM(1,1)

灰色預測方法的特點：首先把離散數據看作連續曲線上的離散值，由于連續函數可微分，從而轉變為微分方程處理這些數據；其次由原始數據產生累加生成數，對累加生成數使用微分方程模型，以便找到數據的規律性。灰色系統理論的微分方程模型為GM(1,1)[1]，表示1階的、1個變量的微分方程。

設有原始數據列X(0)為

X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)} ,

(1)

式中n為數據個數。根據X(0)數據列建立GM(1,1)來實現預測功能，得預測后數據為

(2)

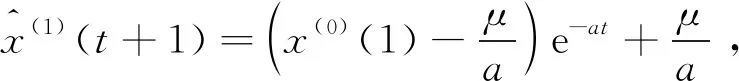
可得

(3)

式中：a為灰色發展系數；μ為灰色作用量。

2 首輸入GM(1,1)

2.1 傳統GM(1,1)原始數據列的首項x(0)(1)無效

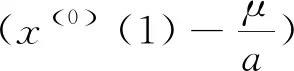
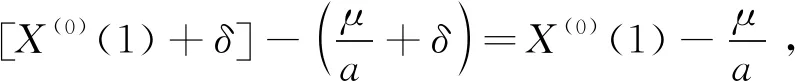
(4)

因此，由GM(1,1)得到的模擬值以及預測值，均與任意常數δ和原始數據列的首項無關。

2.2 FGM(1,1)建模方法

在原始數據首項前加入任意常數，以便獲取原始數據列首項的信息。FGM(1,1)的具體建模方法如下：設原始序列為

X(0)={X(0)(0),X(0)(1),X(0)(2),…,X(0)(n)},

其中首項X(0)(0)為任意常數。由最小二乘法得

t=1,2，…,n。

這樣原始數據的首項信息也被利用，原始數據的整體性不被破壞，FGM(1,1)預測得到的數據更加準確。

3 變權緩沖GM(1,1)

3.1 基于變權緩沖算子的數據預處理

傳統緩沖算子是一恒量，緩沖效果不是過弱就是過強，因此對于數據預處理適應性不強。把緩沖算子進行變權弱化以及運用背景值優化對傳統GM(1,1)進行改進[8]，可實現對原始數據預處理動態化，增強數據適應性。設X=[x(1),x(2),…,x(n)]為原始數據列，有

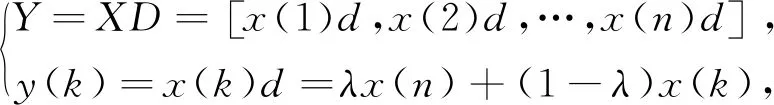
(5)

式中：0≤λ≤1；x(k)>0，k=1,2,…,n。當X為單調增、單調減或振蕩序列時，稱D為變權弱化緩沖算子，λ為變權緩沖系數。設原始數列為非負序列系統，r(k)表示數據序列X中從x(k)到x(n)的平均變化率，X經緩沖算子D作用后的數據序列為，XD=[x(1)d,x(2)d,…,x(n)d]，則稱

(6)

為緩沖算子D在k點的調節度[9]。緩沖算子D在各點調節度均為常數，且與變權緩沖系數相等，即δ(k)=λ。

3.2 變權緩沖GM(1,1)建模過程

構建變權緩沖GM(1,1)(VWGM)建模，使用變權緩沖算子D對原始數據預處理，并構造變權背景值Z(1)

(7)

式中η為背景值生成權重系數，0≤η≤1。通過最小二乘法求解，累減還原得預測值

(8)

上述模型是傳統GM(1,1)的拓展，當λ和η取0.5時，模型退化為傳統GM(1,1)。

3.3 基于灰色關聯分析和粒子群優化算法的模型參數優化

為尋找最優λ和η值，用粒子群優化算法求解[10]，可得到最優解。為確保預測結果最大限度保持原有數據內在變化規律，避免陷入局部最優，基于灰色關聯分析，以擬合值與實際值的灰色關聯度最大構建適應度函數。

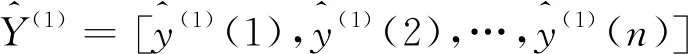
(9)

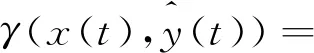
(10)

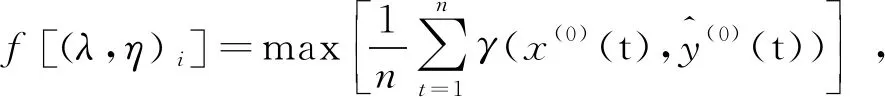
4 混合GM(1,1)

由以上論述知，FGM(1,1)以及VWGM各有其優點和其不足，經分析驗證，其優缺點是可以互補的。將以上兩模型整合得到混合GM(1,1)(HGM(1,1))，這就可以充分利用兩者的優點，避免缺點影響預測結果。HGM(1,1)的具體建模步驟如下：

1)基于灰色關聯分析和粒子群優化算法優化模型參數。

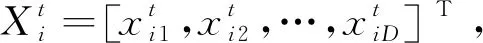
(11)

式中：t為粒子當前更新迭代次數；c1和c2為加速因子，均為常數；r1和r2為[0,1]區間的隨機數；ω為慣性權重因子。粒子通過式(11)不斷更新速度和位置，直到到達最大迭代次數或搜索到的位置滿足預定適應度值時停止搜索；

2)利用FGM(1,1)對原始數據列處理，步驟如3.2中所述。

3)利用1)中求解的最優參數λ和η，對原始數據列進行預處理并求出預測。

(1)使用變權緩沖算子D對原始數據列預處理，弱化隨機性增強趨勢性，得處理后

(12)

(2)一次累加生成，將預處理后的數據進行累加得

(13)

(3)構造變權背景值Z(1)

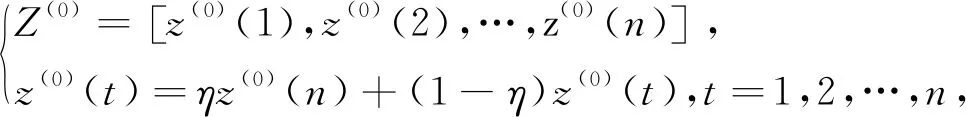
(14)

式中η為背景值生成權重系數，0≤η≤1。構建GM(1,1)模型y(0)(t)+az(1)(t)=μ式中a和μ為模型的灰色發展系數和灰色作用量，可通過最小二乘法求解,求得模型的解，累減還原得預測值

5 實例分析

為了檢驗分析HGM(1,1)模型在中長期預測中的有效性，用文獻[11]中的數據對模型進行驗證。以某地1998—2005年負荷數據為建模數據(表1)，對2006—2008年的負荷進行預測。由表1可知建模負荷數據既有逐年增長的趨勢，也有不確定的波動。分別使用4種模型建模預測，擬合結果見表1，預測結果見表2。

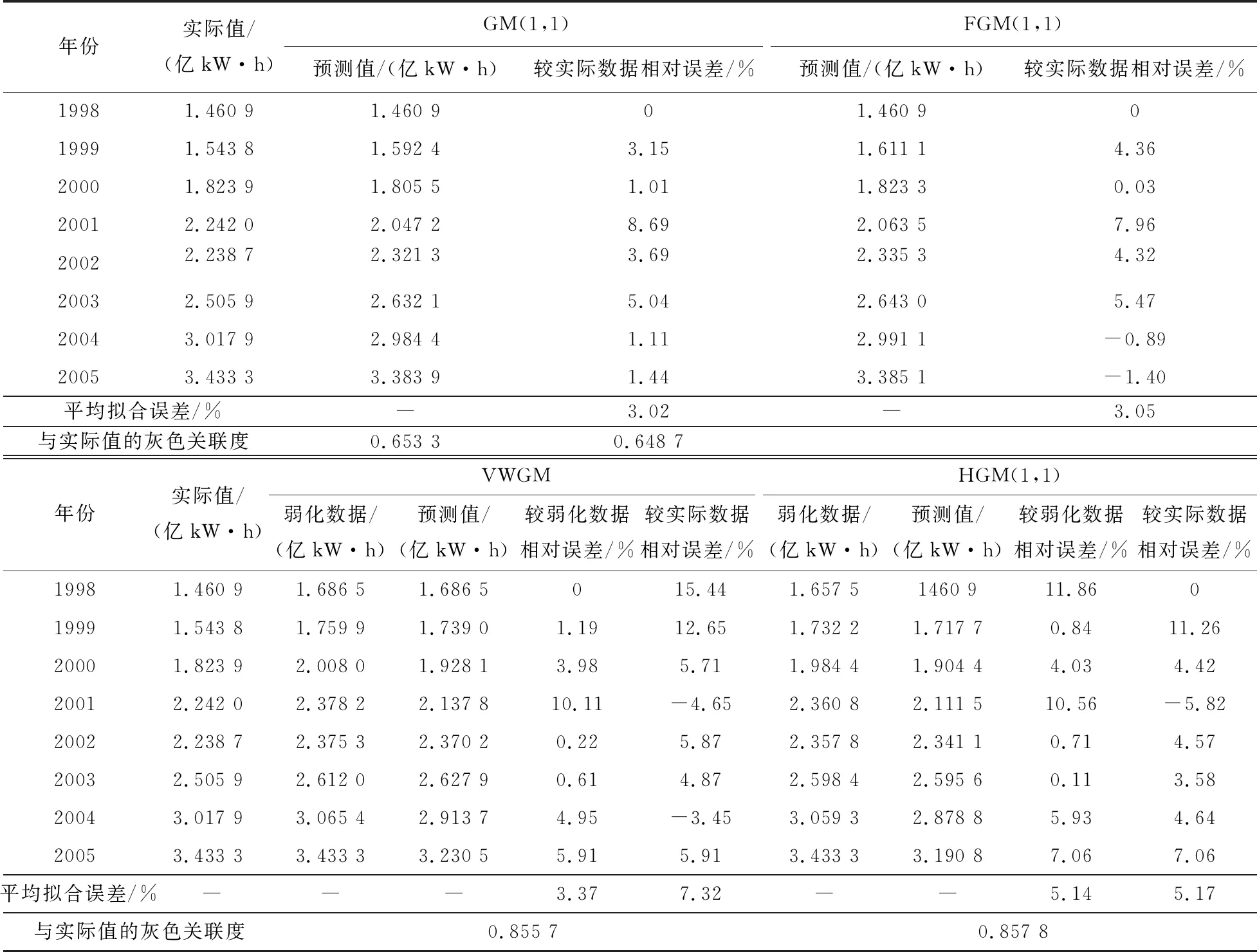
表1 四種模型的擬合結果

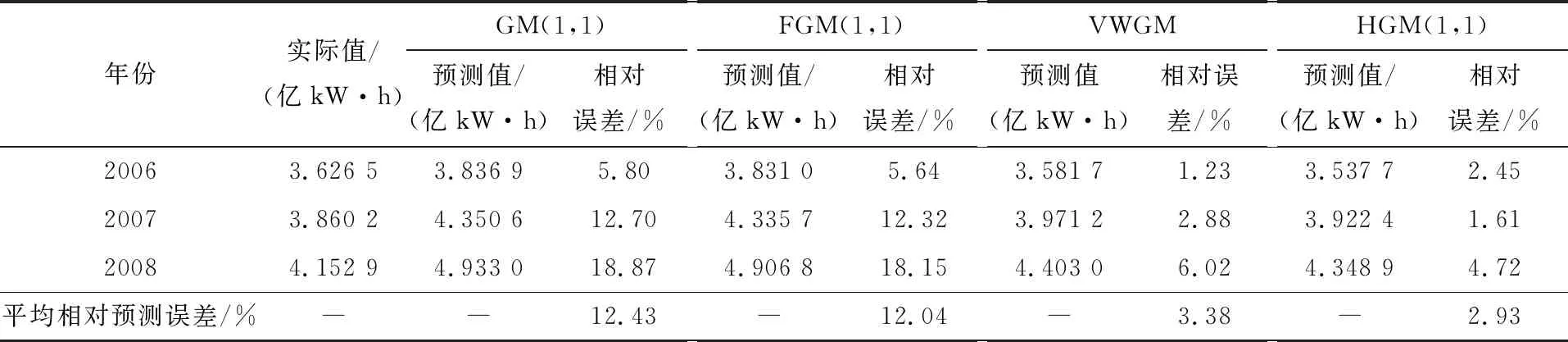
表2 四種模型的預測結果

模型1為傳統GM(1,1)，平均模擬相對誤差為3.02%，擬合效果不錯，但沒有把握和弱化原始數據的波動性，平均預測相對誤差達到了12.43%，預測效果不好。

模型2為改進模型FGM(1,1)，平均模擬相對誤差為3.05%，擬合效果也不錯，但是平均預測相對誤差達到了12.04%，較傳統GM(1,1)有所改進，預測效果仍不好，但它有充分利用原始數據列的優點。

模型3 用粒子群優化算法選擇最優的變權緩沖系數，粒子群算法基本參數設置為：種群規模m=30，最大迭代次數tmax=2 000，c1=c2=2，ωmax=0.9，ωmin=0.4，尋得模型最優參數為λ=0.1144，η=0.756 7。擬合值較實際值的平均擬合相對誤差為7.32%，灰色關聯度為0.855 7，平均預測相對誤差為3.38%，擬合與預測效果較穩定，對于中長期預測精度較高。

模型4 仍采用模型3運用的粒子群優化算法選擇最優的變權緩沖系數，粒子群優化算法基本參數設置相同，尋得模型最優參數為λ=0.099 7，η=0.754 6。然后與模型2進行整合優化，形成混合HGM(1,1)模型，由表可知，擬合值較實際值的平均擬合相對誤差僅為5.17%，灰色關聯度為0.857 8，平均預測相對誤差僅為2.93%。擬合與預測效果較以上模型均更加較穩定可靠，與以上所有模型相比，無論在實際值擬合誤差，預測值擬合誤差，平均擬合誤差，灰色關聯度等等性能指標均優于以上所有模型，非常適用于中長期預測，性能改進明顯。

6 結束語

提出的模型引入粒子群優化算法、變權緩沖算子以及FGM(1,1)模型，先對原始數據進行動態預處理，再通過變權緩沖系數對算子作用強度實現微調，這樣就有效解決了傳統緩沖算子作用強度不可調、緩沖效果過強或過弱的問題，以及忽略首項原始數據信息造成的信息不完整等問題，增強了模型的適應性，充分利用原始數據信息，提高模型的預測精度，實用性很強。

其次，提出的模型以擬合值與實際值的灰色關聯度最大為目標進行參數優選，運用灰色關聯分析和粒子群優化算法，充分運用所有原始數據信息，最大程度地保持了原始數據的內在變化規律，實現了數據預處理與原有預測問題的有機統一，模型擬合與預測效果均更加穩定可靠。模型可以運用到環境管理、資源管理、城市規劃等實際生活當中。