高效的基于數據與模型的信道估計算法

梅鍇，趙海濤，劉瀟然，劉軍，熊俊，任保全，魏急波

（1.國防科技大學電子科學學院，湖南 長沙 410073；2.軍事科學院系統工程研究院，北京 100076）

0 引言

近年來，機器學習技術的研究取得了進展，相關前沿技術成功應用到了語音識別、圖像識別、自然語言處理以及機器視覺等領域[1]。這也激起了在無線通信系統中應用機器技術的研究熱潮。機器學習獲得廣泛關注的重要原因之一是它具有強大的數據挖掘能力。具體而言，它通過在大規模數據集上訓練神經網絡，以挖掘出數據中的潛在規律，從而完成復雜任務。目前，大多數研究也是利用機器學習技術的這一特性，突破無線通信系統中的瓶頸問題。其中，一些研究提出用深度神經網絡（DNN,deep neural network）來代替無線收發機系統的物理層中的某一個模塊，比如數據檢測[2]、信道估計[3-5]、信道譯碼[6]等，甚至是完全打破傳統的無線通信系統結構，將收發機分別用一個神經網絡實現[7-8]。

這類方法將神經網絡視為黑盒子，依靠大規模訓練數據集賦予神經網絡所需的功能。這在一定程度上簡化了工程師需要承擔的工作，并且在模型難以精確描述系統的復雜場景下，其取得的性能可超越經典基于模型的算法中的最優方案。然而，這類方法也存在幾點固有的局限性[9]。首先是訓練問題。目前，在通信領域還沒有用于訓練和測試的標準化數據集。此外，網絡需要預先進行離線訓練再使用。在使用過程中，網絡的參數不能再進行調整，因此難以應對動態變化的無線通信環境。再者是可解釋性。現在并沒有一種系統的方式來理解深度學習方法成功與否背后的原因。這導致很難再進一步改進基于深度學習（DL,deep learning）的算法。最后是基于深度學習的方法需要消耗大量計算資源以及存儲資源，在目前大多數通信設備中都難以直接應用。

不同于圖像識別等機器學習成功應用的領域，通信系統設計有堅實的理論作為支撐，并且無線通信技術已歷經幾十年發展，現有基于模型的解決方案有著很好的性能。因此，一些研究通過結合2 種方法各自的優勢對現有系統進行改進，設計更具實踐價值的算法。這類方法稱為基于混合數據與模型的方法，或者數據與模型聯合驅動下的方法[9]。現有相關研究可以粗略地分為2 種：模型驅動的機器學習方法[4,10-11]和增強模型的學習方法[9]。

模型驅動的機器學習方法的基本思路是將通信系統的領域知識集成到神經網絡，建立模型驅動的深度學習框架。這樣的設計范式不依賴于準確的模型假設，而是利用數據來提升性能。同時，獲得了一些模型帶來的優勢，比如降低訓練所需的數據量。然而，這類方法依然面臨著訓練與可解釋性方面的問題。

增強模型的學習方法的基本思路是利用數據訓練一個自適應的信道模型，然后直接通過訓練好的模型設計算法。這類方法不是利用數據直接去修正或者訓練一個算法，而是利用數據從備選模型中選出一個符合當前真實環境的模型來完成模型的修正。該方法與模型驅動的機器學習方法的顯著差別在于訓練過程中，通過修正模型所學到的是模型參數，這些參數是有具體的物理意義的。這樣可以帶來幾點好處：1)基于有具體的物理意義的參數進行設計，使算法具有理論解釋；2)在基于修正模型設計算法時，由于存在閉合表達式，不再需要訓練數據，可以在線完成算法設計，因此，可以適應動態變化的無線通信環境；3)相比基于數據的網絡，待學習的參數被極大地降低，這樣模型修正所需要的數據在實際系統中是可以保證的。然而，這類方法不具備無模型特性帶來的優勢。當備選模型都不符合當前真實信道環境時，這類方法仍存在由模型失配帶來的問題。

上述2 種基于混合模型與數據的方法分別以基于模型的方法或者基于數據的方法為側重點，從最終的算法特性上看，很大程度上會與其中一種方法保持一致，所以會保留其中一種方法的局限性。本文探索一種更為折中的設計范式，更深層次地融合2 種方法，從而得到一種具有全新特性的算法。本文基于文獻[12]提出的信道估計方法進一步融合基于模型的方法設計信道估計算法。文獻[12]針對目前常用通信體制的基礎單元——正交頻分復用（OFDM,orthogonal frequency division multiplexing）系統，提出了一種可在線訓練的學習型估計器。由于該方法采用在線訓練的模式，因此可以適應動態無線通信環境。此外，學習模塊采用線性結構，計算復雜度低，并且便于從理論上解釋其成功實現信道估計的原因[13]。在該方法中，訓練數據的生成依賴于塊狀導頻，即一個OFDM 符號內所有子載波都傳輸導頻信號。通常，在基于數據的方法中，訓練數據僅用于訓練，不能用于完成最終的任務，所以發送塊狀導頻僅僅是為了對估計器進行訓練。而在經典的估計方法中，利用塊狀導頻本身就可以完成信道估計任務。因此，本文進一步借助基于模型的方法，以數據與模型聯合驅動的方式，實現對訓練數據的高效使用。具體而言，在用塊狀導頻生成訓練數據進行訓練后，直接將訓練結果用于塊狀導頻上的信道估計任務，以提升系統效率。

本文主要的研究工作如下。

1)針對采用塊狀導頻的OFDM 系統，提出一種數據與模型聯合驅動下的信道估計算法。該算法利用訓練數據獲得了比傳統信道估計算法更好的性能，同時利用模型使訓練數據可用于完成信道估計任務，避免了因生成訓練數據所導致的系統效率的損失。首先利用塊狀導頻基于最小二乘（LS,least square）估計獲得信道頻率響應的初始估計結果，然后通過濾波處理抑制LS 估計結果中的噪聲，從而提升估計精度。其中，濾波器的系數以數據與模型聯合驅動的方式獲取，主要包含2 個步驟：以基于數據的方法獲取插值系數和以基于模型的方法利用插值系數解析地求解濾波器系數。

2)基于文獻[12]提出的方法，設計了基于數據的插值系數獲取方案。文獻[12]構造了一種可在線獲取的訓練數據結構，并提出基于該訓練數據學得具備信道估計功能的線性模型。事實上，該線性模型屬于一種插值器，而線性模型的系數即插值系數。本文對該方法進行了擴展，設計了可通過訓練獲取插值系數的算法的一般形式，以求得求解濾波系數所需的插值系數。

3)在最小均方誤差（MMSE,minimum mean square error）準則下，推導了一種濾波系數展開為插值系數表示的解析關系，使基于數據所獲取的學習結果，即插值系數，能夠用于實現濾波功能，完成信道估計任務。這使塊狀導頻不僅可用于生成訓練數據，還可用于實現信道估計，從而實現了對訓練數據的高效使用，提升了系統效率。

4)本文對本文算法的可行性與復雜度進行了分析。此外，基于OFDM 系統進行了仿真實驗，仿真結果驗證了本文算法的性能、穩健性以及對實際非理想因素的適應性。

1 系統模型與問題描述

OFDM 系統結構如圖1 所示。令x=[x1,…,xK]T表示經過調制的發送信號，y=[y1,…,yK]T表示頻域接收信號，上標T 表示轉置。假設接收機的時頻同步準確，第k個子載波上的接收信號可表示為

圖1 OFDM 系統結構

其中，zk為高斯白噪聲；hk為第k個子載波上的頻率響應，通常假設hk為平穩隨機變量且服從零均值復高斯分布。令h=[h1,…,hK]T表示信道頻率響應；r(Δ)表示信道的自相關系數，即r(Δ)=，其中 E[·]表示求解期望，上標*表示共軛操作。不失一般性地，本文假設信道響應功率為1，即r(0)=1。

文獻[12]針對OFDM 系統提出了一種學習型信道估計方法。該方法可以在線收集訓練數據，并實時地快速地完成訓練，這有助于通信系統的智能化發展[14]。本文首先對該方法進行簡要介紹。考慮學習模塊的輸入維度為2，輸出維度為1，則學習模塊可表示為

由式(2)可以看出，學習模塊的輸出是輸入的線性組合，或者叫加權和。這不同于很多現有的基于機器學習的信道估計方案，在現有方案中，輸出通常是輸入的非線性映射。相反，上述方案與大多數基于模型的信道估計方法在結構上是一致的，因為許多經典的信道估計方法都可以表示為式(2)的形式[17]。由于結構上與經典算法是一致的，這使上述基于機器學習（或者基于數據）的方法便于與經典的基于模型的算法相結合。

在上述方法中，為通過訓練獲得插值系數ω，需要發送一個額外的塊狀導頻符號，即一個OFDM符號中所有的子載波都傳輸導頻信號。首先，利用塊狀導頻基于LS 估計算法獲得信道的頻率響應，如式(3)所示。

其中，w=[w1,w2,w3]T為3 維向量，包含連接輸出與輸入的3 個權系數，在本文中稱w為濾波系數。

從另一個角度講，上述過程也違背了機器學習的一般流程。在一個機器學習任務中，訓練數據通常只用于用來優化學習模塊參數，任務是在后續新的數據上完成的。上述過程是要實現在利用生成訓練數據并學得濾波系數w后，又直接將學得的w用于處理得到更高精度的估計。這意味著訓練數據不僅用于優化學習模塊參數，還要完成最終任務，這在通常的機器學習方法中是不可實現的。因此，僅憑借文獻[12]中的方法無法完成上述設計目標。

本文考慮在文獻[12]的方法基礎上，進一步借助基于模型的方法來實現上述目標。采用基于模型的方法推導出濾波系數展開為插值系數的表達式，其中，插值系數用文獻[12]的方法以基于數據的方式得到。這樣以數據與模型聯合驅動的方式可以實現通過訓練優化信道估計，同時訓練過程不會造成額外數據消耗。

2 算法設計

2.1 基于模型部分的算法

在現有基于模型的方法中，有多種計算濾波系數、插值系數的方式。眾所周知，其中的最優方法是MMSE 算法[18]。因此，本文在MMSE 準則下推導出濾波系數展開為插值系數的表達式，作為基于模型部分的算法。

以濾波系數w為例，MMSE 準則可以表示為如下優化問題

式(6)從形式上看是線性最小均方（LMMSE,linear MMSE）準則，但在本文考慮的模型下，MMSE準則與LMMSE 準則下的算法有相同的解析形式[18]。推導借鑒經典的卡爾曼濾波器的推導思路[18]。以上述濾波任務為例，在卡爾曼濾波中，為了得出對g1的估計，首先求解出對g1的MMSE 估計，該過程稱為預測。然后求解包含的新息，新息是指中與不相關的那一部分，求新息的過程也稱為正交化。在對g1的預測基礎上加入新息對g1的MMSE 估計，最終得出對g1的MMSE 估計。

其中，ωa表示估計g1的MMSE 插值系數，；表示對g1的MMSE 估計，為新息。附錄1 推導了的表達式，如式(8)所示。

其中，r1,2=[r(1),r(2)]T表示h的自相關向量，H 表示共軛轉置，表示中包含的噪聲的功率。

令bm為估計g1+m的MMSE 插值系數，有

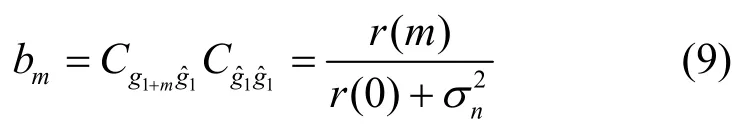
將式(9)代入式(8)中，式(8)可進一步化簡為

其中，ωb=[b1,b2]T，b1和b2分別為m=1 和m=2 時bm的值。將式(10)代入式(7)，可得

在式(11)中，等式右邊除b0外，變量均為插值系數。注意到，本文的目標是將濾波系數展開為插值系數，即等式右邊的參數均需為插值系數。否則，等式右邊的變量將不能用基于數據的方法統一求解。因此，本文用近似替代b0，可得出由插值系數ωa和ωb求解w的公式，即

至此，本文得出在MMSE 準則下，濾波系數展開為插值系數的表達式。

基于模型部分的算法為根據式(12)，利用插值系數計算出濾波系數w。

2.2 基于數據部分的算法

基于第1 節介紹的可在線訓練的學習型信道估計方法，獲取插值系數ωa和ωb。

令ω為待學習的參數，有yO=ωTxI。這樣可以對不同訓練數據集的訓練算法做統一的闡述，也就是對ωa和ωb的獲取算法做統一描述。

上述優化問題存在解析解，即

式(14)即基于數據求解插值系數的方法。由于訓練通過求解解析解完成，因此該訓練過程總能獲得最優參數。針對不同的插值系數，利用，根據文獻[12]中導頻輔助的訓練數據生成（PATDG,pilot aided training data generation）方案產生相對應的訓練數據。對于ωa，XI和分別為(K-2)×2維矩陣和(K-2)×1維向量，其具體形式為

對于bm(m=1,2)，XI和分別為(K-2)×1維矩陣和(K-2)×1維向量，其具體形式為

2.3 算法流程

其中，系數w為M維向量。

w擴展為M維向量后，基于模型部分的算法，即式(12)給出的濾波系數與插值系數的解析關系需要相應擴展。而基于數據部分的算法，即式(14)為一般形式，所以不需要進行修改，但式(15)和式(16)給出的訓練數據集的形式需要進行擴展。

式(12)擴展后的形式為

其中，插值系數ωa、ω b為M-1維向量。可以看到，式(18)與式(12)的形式基本一致。這是因為在第2.1 節基于模型部分的算法的推導中，所采用的參數的符號標記不受w的維度的影響，因此便于對推導結果進行擴展。

為獲取ωa，式(14)中XI和的具體形式為

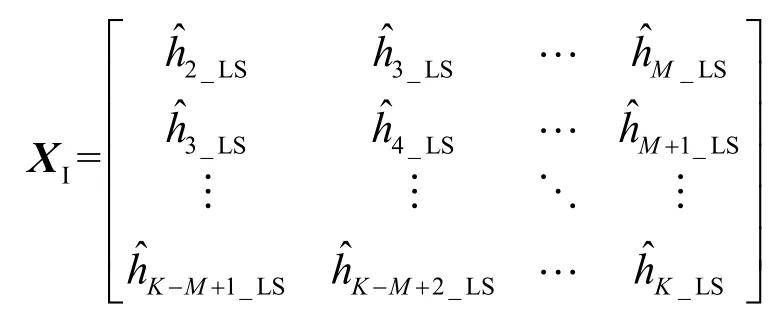
為獲取ωb中的bm(m=1,…,M-1)，式(14)中XI和的具體形式為

基于第2.2 節介紹的基于數據的插值系數獲取方法以及第2.1 節設計的濾波系數與插值系數的解析關系，可以設計一種數據與模型融合驅動的信道估計算法，如圖2 所示。算法流程如下：首先，利用生成訓練數據，如式(19)和式(20)所示；然后，用基于數據的方法，即式(14)，得到插值系數ωa、ωb，再通過基于模型的方法，即式(18)，由ωa、ωb求解出濾波系數w；最后，利用得到的濾波器對進行處理，抑制中的噪聲，完成整個信道估計任務。

圖2 信道估計方法流程

從圖2 可以看到，不同于基于模型的方法，算法中沒有用到信道的統計參數。以一種典型的基于模型的方法——MMSE 算法為例，在該算法中需要用到關于中包含的噪聲的功率以及h的自相關函數等信息。在實際系統中，這些關于的統計模型的信息是未知的，通常需要通過較為復雜的算法來獲取。此外，獲取參數的偏差還會帶來性能損失。而本文算法中不需要用到模型參數，所以避免了上述問題。

本文算法也不同于基于數據的方法，算法中的訓練數據可以直接用于完成信道估計任務。根據現有基于數據的方法（基于機器學習的方法），為學得估計器，首先需要一個數據集，該數據集可以是通過仿真離線生成的[4]，也可以是基于塊狀導頻生成的[12]，在使用估計器時，又是基于新的數據，數據集的作用僅僅是用于訓練。而在本文算法中，導頻信號既可以用于產生訓練數據，又可以用于完成信道估計任務，從而大幅提升了數據使用的效率。

通過數據與模型融合驅動的方式，本文算法集成了基于數據的方法和基于模型的方法各自的優勢。基于數據的方法使算法不需要模型參數，避免了模型參數的獲取以及由于參數偏差導致的性能損失。基于模型的方法使訓練數據可以用于完成最終任務，從而提升數據使用的效率。

3 性能分析

3.1 可行性分析

本節主要分析本文算法結合基于數據的方法與基于模型的方法的可行性，以及在本文算法中訓練數據可被使用的原因。

文獻[12]已經驗證了當樣本量充足時，用其提出的基于數據的方法可學得插值器，且其性能十分接近于MMSE 插值。所以在樣本量充足的條件下，基于數據的方法可以視為一種MMSE 插值的近似實現方式。為保證基于數據部分的算法有充足的訓練數據，需要h有較高的維度，即一個OFDM 符號中包含較多的子載波，如子載波數為512、1 024 等。此時，所提的數據與模型融合驅動下算法可視為一種針對MMSE 準則的算法。具體而言，首先用基于數據的方法獲得近似的MMSE 插值系數，然后用MMSE 準則下插值系數與濾波系數的解析關系得出近似的MMSE 濾波系數。因此，本文算法可以視為一種以基于混合數據與模型的方式實現MMSE 估計的算法。

值得注意的是，濾波系數w不僅可用于處理產生訓練數據的LS 估計，也可用于處理與獨立同分布的數據。換言之，計算得出w后，在信道統計特性不變的情況下，可以直接用之前計算得到的w處理本次塊狀導頻上的LS 估計結果。這受益于基于數據方法的泛化能力。從另一個角度講，由于w是近似的MMSE 濾波系數，在信道統計特性不變的條件下，MMSE 濾波系數不變，因此只用計算一次濾波系數w，后續塊狀導頻上的信道估計可以直接使用此次計算的w的值。

本文算法可以使用訓練數據最重要的原因在于其特殊的訓練數據結構。在通常的基于數據的方法中，訓練數據不會被使用的原因在于，訓練數據的標簽一般為輸入數據所對應的理想輸出。對于訓練數據，由于理想輸出是已知的，因此輸入這部分數據所得到的輸出沒有價值。因此，通常的訓練數據僅用于訓練，不會被再次使用。而在本文算法中，訓練數據的標簽是信道響應的LS 估計結果，并非理想輸出（準確信道響應h）。LS 估計結果對噪聲功率敏感，通常需要進一步處理以抑制噪聲影響，所以在理想輸出未知的條件下，訓練數據仍具有使用的價值。

3.2 復雜度分析

本節采用復數乘法（CM,complex multiplication）的數目來表征計算復雜度。為了簡化，令Cpinv(NM2)、Cinv(M3)分別表示計算M×N(M＜N)矩陣廣義逆和M×M矩陣逆的復數乘法數目。

本文算法可以分為2 個步驟，即計算濾波系數w和用w對LS 估計結果進行濾波處理。其中，第二個步驟包含了MK次復數乘法，M和K分別為w的維度和的維度。對于大多數方法，這個步驟的計算量是相同的，主要區別在于計算w的復雜度。

在本文算法中，計算w需要(M-1)(Cpinv(N)+2N+1)+Cpinv(N(M-1)2)+M次復數乘法，其中N為訓練數據量。在MMSE 信道估計中，計算w需要Cinv(M3)+M2次復數乘法。實際系統中，信道響應的相關系數和噪聲功率通常是未知的，所以MMSE 信道估計通常還需要額外的運算以獲取其所需的統計信息。本文算法的計算復雜度比MMSE信道估計稍高，甚至與之相當。

4 仿真分析

為驗證本文算法的性能，本節搭建了OFDM 仿真系統，系統模型的數學表達式如式(1)所示，系統參數如表1 所示。本節將通過仿真實驗對本文算法的參數設置（即輸入維度M）進行討論，檢驗其穩健性與對實際非理想特性的適應性，以及與現有方法進行對比。采用如式(21)所示的歸一化均方誤差（NMSE,normalized mean square error）衡量信道估計的性能。

表1 系統參數

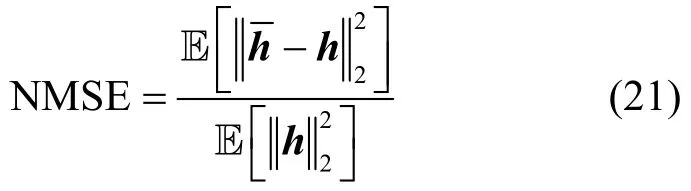
在仿真中，假設一幀內的信道響應不變，而不同幀之間的信道響應相互獨立。信道延遲功率譜（PDP,power delay profile）采用指數衰減譜[15]，如式(22)所示。

其中，C表示歸一化系數，τmax表示最大多徑時延。

圖3 比較了不同輸入維度下本文算法的NMSE性能。通常，輸入維度M越高，估計性能通常越好。但在本文算法中，M越高，基于數據部分的算法所需的訓練數據量越大。由于每個導頻符號可提供的訓練數據量是固定的，因此隨著M的增加，所提供的訓練數據將難以滿足訓練需求，這將導致基于數據部分的算法性能下降，最終導致整個信道估計性能的下降。因此，M值的選取需要根據實際提供的訓練數據量選擇一個適中的值。根據式(20)易得訓練數據量等于K-M+1，其中K對應一個OFDM符號中的可用子載波數，仿真中K=410。從圖3中可以發現，隨著M的增加，信道估計的性能先是逐漸提升，但是當M=8 時，在高信噪比下，其性能較M=7 有所下降；當M=10時，在低信噪比下，其性能仍略有提升；當M=30時，與M=10相比，M的增加反而導致性能有明顯下降。這說明在K=410時，M最優的取值是7。M在趨近7 時，訓練數據量逐漸難以滿足基于數據部分算法的訓練需要。再增加M，不僅會導致計算復雜度的增加，還可能導致性能的降低。

圖3 不同輸入維度下本文算法的NMSE 性能

圖4 進一步仿真了本文算法的NMSE 性能隨可用子載波數的變化。令信噪比（SNR,signal to noise ratio）為0，通過調整虛擬子載波數目來控制可用子載波數K。從圖4 中可以看到，在K較小時，本文算法的性能有明顯損失，特別是在M取較大值時。隨著K的增大，本文算法的NMSE 逐漸下降。對于M≤4，當K>300，NMSE 的下降趨于平緩，說明此時提供的訓練數據已較為充足。對于M≥5，當K接近410 時，NMSE 的下降趨勢仍較為明顯，說明一個OFDM 導頻符號所能提供的數據不足以滿足其訓練需求。在后續的仿真實驗中，為保證基于數據部分的算法的訓練數據量充足，M取較小的值4。

圖4 本文算法的NMSE 性能隨可用子載波數的變化

圖5 仿真了不同最大多徑時延下本文算法與LMMSE 算法的性能對比。不同最大多徑時延取值表征了不同的信道環境。仿真中將本文算法與LMMSE算法進行對比。與本文算法相同，LMMSE 算法算法也使用一個塊狀導頻符號。從圖5 可以發現，當SNR在0 左右時，本文算法性能均十分接近LMMSE算法，這說明本文算法對于信道環境有穩健性。此外，還可以看到，在低信噪比下，本文算法相比LMMSE 算法有較大的性能損失，這是由噪聲能量對基于數據部分的算法性能的影響導致的[12]。此外，在高信噪比下，當τmax=8 μs 時，本文算法也會產生性能損失。針對此現象，下一個仿真實驗將會進行深入分析。

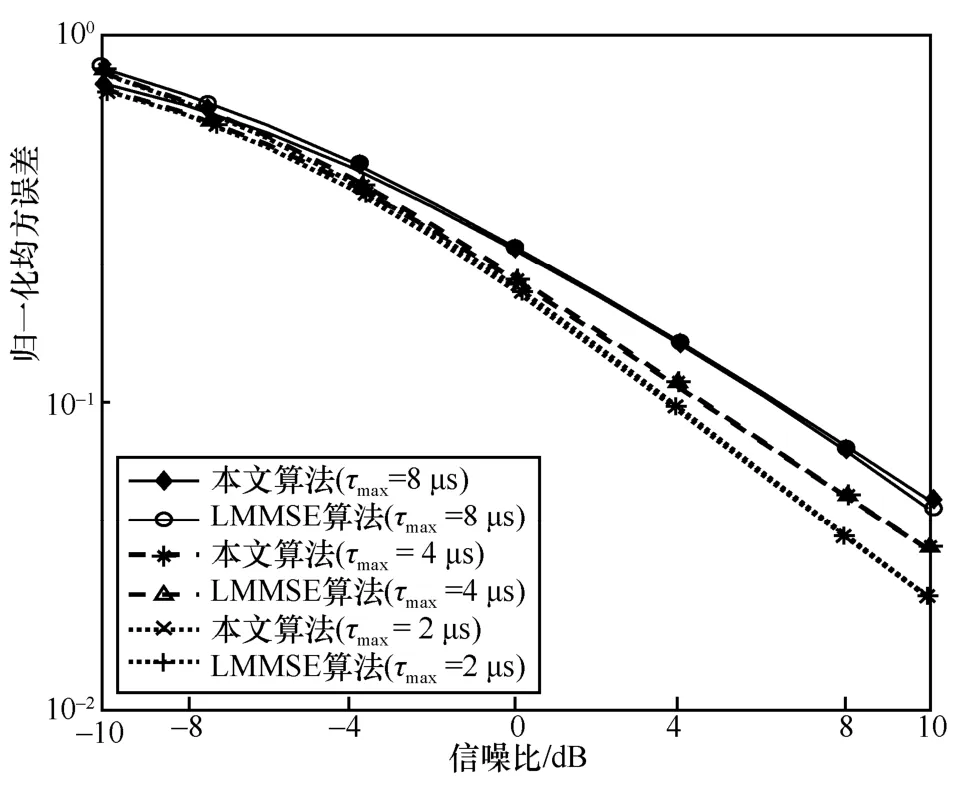
圖5 不同最大多徑時延下本文算法與LMMSE 算法的性能對比

圖6 仿真了極高信噪比下本文算法的性能。從圖6 可以看到，隨著信噪比的增加，性能反而會變差，這是因為在基于模型部分的推導中，本文用參數近似地替換b0，如式(12)所示。該近似導致的性能損失在高信噪比下尤其明顯。曲線修正算法代表的是本文算法在基于模型部分采用精確b0值的性能。值得注意的是，由于b0精確已知的條件在實際系統中不能滿足，因此修正算法僅用作性能分析，不具備實踐性。

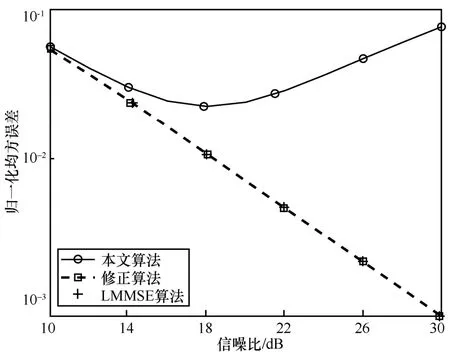
圖6 極高信噪比下本文算法的性能

從圖6 中可以看到，修正算法在極高信噪比依然十分接近于LMMSE 算法。這表明本文算法在高信噪比下的性能損失主要是由用替換b0的近似操作導致的，而b0又不能通過基于數據的方式獲取。如何補償該近似造成的高信噪比下的性能損失是本文算法面臨的一個難題。

圖7 比較了本文算法與經典估計算法在不同信噪比下的NMSE 性能。雖然本文算法的性能會稍微劣于理想LMMSE 算法，但在實際系統中，信道估計的統計參數未知，需要通過估計獲取。相比采用估計參數的LMMSE 算法[20]（估計信道統計參數利用的是同一塊狀導頻符號），本文算法有明顯的性能優勢，特別是在低信噪比條件下。這是因為在低信噪比下，信道二階統計參數的估計存在較大偏差，導致整體估計性能的惡化。而本文算法受噪聲功率的影響要小很多。該仿真結果說明，當實際系統中的信噪比條件較差時，采用本文算法的系統性能將明顯優于基于LMMSE 估計原理的信道估計算法。

圖7 本文算法與經典估計算法在不同信噪比下的NMSE 性能

基于數據的方法的一個重要的優勢是可以適應實際非理想特性。文獻[12]中的方法可以通過學習補償實際非理想的影響。為檢驗本文算法是否保留了這一特性，本文仿真了存在定時誤差（STO,symbol timing offset）的場景下本文算法的性能。仿真中，假設STO 均勻分布于[θmin,…,0]。為進一步體現信道估計對系統性能的影響，本文用誤碼率（BER,bit error rate）來表征信道估計性能，采用迫零均衡（ZF,zero-forcing）和硬判決來恢復信息比特。

圖8 描述了不同θmin取值下3 種算法的性能對比。在該場景下，信道自相關函數會隨STO 的值變化，進而影響LMMSE 算法的性能[21]。因此，在不考慮STO 的影響時，LMMSE 算法有明顯的性能損失。在修正LMMSE 算法[21]中，利用STO 的統計信息可以補償STO 對LMMSE 算法造成的影響，從而提升信道估計的性能。在本文中，稱修正LMMSE也為平均LMMSE（ALMMSE,average LMMSE）。從圖 8 中可以看到，本文算法的性能仍優于ALMMSE 算法，并且θmin的取值越小（定時誤差越大），優勢越明顯。這是因為基于數據部分的算法可以利用訓練數據學到定時偏差并且很好地進行了補償，所以本文算法也可以很好地補償STO 產生的影響。

圖8 不同 θmin 取值下3 種算法的性能對比

圖9 比較了本文算法與2 種基于深度學習的信道估計算法的性能[3,22]。信道條件與圖8 對應的實驗相同，且θmin=-4 0。在仿真中，本文假設采用基于深度學習的信道估計的系統可以利用仿真數據進行離線訓練（數據量為 2×107），并且除信噪比外，訓練階段信道的統計特征與使用時一致。訓練階段的信噪比為可能的最大值[3]，即10 dB。卷積神經網絡（CNN,convolutional neural network）和DNN 的結構在原文獻的基礎上進行了調整，使之與本文算法的輸入與輸出保持一致，輸入層和輸出層維度分別為8 和2。CNN 的卷積核大小為3×3，有3 個卷積層，分別包含4、8、8 個卷積核。DNN 有3 層，其中隱藏層包含20 個神經元。除輸出層外，激活函數為ReLU，輸出層激活函數為線性函數。從圖9 中可以看到，本文算法的性能優于2 種基于深度學習的信道估計算法。這是因為在這2 種算法中訓練階段和使用階段是分離的過程，且使用階段不能進行訓練。而本文算法結合數據與模型，使訓練階段和使用階段采用的是同一批數據，從而保證了2 個階段的數據特征是完全一致的。在使用階段，本文算法通過實時訓練及時適應新的信道條件，如信噪比的改變，從而獲得了更好的性能。

圖9 本文算法與2 種基于深度學習的信道估計算法的性能

從上述仿真結果可以看到，本文算法通過結合數據與模型，彌補了數據與模型各自的不足。相比基于模型的方法，即LMMSE 算法，避免了由于獲取的信道統計參數的誤差而導致的性能損失，在低信噪比下性能優勢尤其明顯。相比基于數據的方法，即基于深度學習的信道估計，避免了由于訓練階段與使用階段數據特征的差異而導致的性能損失，能夠適應信道條件的變化。

5 結束語

本文設計了一種新的數據與模型融合驅動下的信道估計算法。該算法避免了基于數據的方法與基于模型的方法各自的弱點。與基于模型的方法相比，本文算法不需要模型參數，以及可以適應實際非理想特性。與基于數據的方法相比，本文算法可以使用訓練數據，既不需要離線訓練，也沒有因為在線產生訓練數據給系統帶來額外的導頻消耗。為驗證本文算法的性能，本文搭建了OFDM 仿真系統。仿真結果顯示，本文算法具有良好的穩健性以及對實際信道環境的適應性，并且在低信噪比下，其性能明顯優于實際條件下的LMMSE 估計。

附錄1的表達式推導

根據MMSE 的估計公式[18]，有

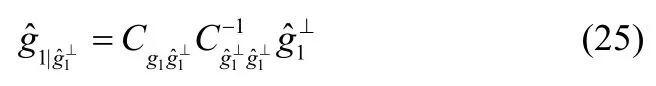
其中，r1,2=[r(1),r(2)]T表示2 維自相關向量。