基于載波相位的高精度室內快速定位算法

范紹帥，榮志強，田輝，李立華

（北京郵電大學網絡與交換技術國家重點實驗室，北京 100876）

0 引言

隨著5G 時代的到來以及無線終端的不斷普及，基于位置信息服務（LBS,location-based service）與人們日常生活的聯系日益緊密。可靠的LBS 基于精準的位置信息，而精準的位置信息由高精度定位技術獲取。因此，高精度定位技術成為近年來定位領域的熱點問題。目前，基于全球導航衛星系統（GNSS,global navigation satellite system）的定位技術已經趨于成熟，在大多數室外定位場景中可以為用戶提供穩定可靠的位置信息，精度可達亞米級。與室外定位場景不同，室內定位場景較復雜。隨著城市建設的不斷發展，包括大型工廠、大型商業中心、大型辦公樓等在內的復雜建筑物與日俱增。建筑物的墻體會造成衛星信號的遮擋，建筑物的結構和其中的物品則會引起復雜的多徑效應。除了定位場景不同，室內定位精度的需求遠遠高于室外定位。已經凍結的5G Release 16 標準要求在室內室外精準定位場景中，定位技術的定位精度需求為米級[1]。考慮到定位技術與工業物聯網等應用的結合，未來Release 17 標準將進一步將室內定位精度提升至厘米級[2]。在智能制造領域，位置信息主要用來提升生產效率及供應鏈管理，對工具防錯以此提高產品質量。智能制造領域的許多應用都需要高精度位置信息，對定位精度有較高要求，精度在厘米級[3]。車輛高精度定位是實現智慧交通和自動駕駛的必要條件。在一些高級的駕駛業務中，如自動駕駛、遠程駕駛和編隊駕駛中，穩定的厘米級定位是其安全可靠服務的必要保障[4]。

目前，主流的室內定位技術，包括射頻識別（RFID,radio frequency identification）定位技術[5]、超寬帶（UWB,ultra wide band）定位技術[6]、超聲波定位技術[7]和雷達定位技術[8]等，已經在特定環境下得到了應用，但是它們往往需要額外的設施部署，導致建設成本較高。在智能制造等典型應用場景中，大量的高速移動機器人、自動導引車（AGV,automated guided vehicle）、可移動裝配平臺和可移動裝配材料工具等移動設備都需要接入現有的蜂窩移動通信系統來完成高可靠低時延通信。結合已部署的網絡進行定位技術，包括基于到達時間（TOA,time of arrival）[9]、到達時間差（TDOA,time difference of arrival）[10]、到達角度（AOA,angle of arrival）[11]和接收信號強度（RSSI,received signal strength indicator）[12]等定位技術，不需要額外部署，但是定位精度不高，只能達到米級。將載波相位測量應用于現有蜂窩通信系統中可以解決上述成本和精度的問題。載波相位最早由文獻[13]提出獨立應用于蜂窩系統，并成為3GPP Release 17 及Release 18的備選定位技術。該技術將系統中傳輸連續的參考信號作為載波相位定位參考信號（C-PRS,carrier phase positioning reference signal），支持終端基于C-PRS 進行載波相位測量。在整周模糊度解算準確的情況下，載波相位可以進行精準的測距。文獻[13]指出將載波相位測量應用到定位中有可能達到亞米級甚至厘米級定位精度。在室內無線環境中，除了信號的多徑效應和噪聲會影響定位精度外，設備之間的鐘差也是一個重要因素。文獻[14]證明了基于TDOA 的定位算法的均方誤差隨著鐘差的L2 范數而增加，文獻[15]證明了鐘差會在載波相位定位的測量值引入誤差項，從而影響定位結果。現有的室內定位算法往往忽略鐘差對定位精度的影響，或者事先對鐘差進行估計。例如，文獻[16-17]采用凸優化的方法來估計鐘差，但估計殘差仍對定位精度有明顯的影響。因此，在實際應用中鐘差的消除對于高精度定位是十分必要的。

此外，實時定位是室內定位的一個典型應用領域，在實際中有著廣泛的應用，如查找定位室內的資產、追蹤定位人員、遠程監控等[18]。以上應用都要求室內定位技術在保證定位精度的條件下可以對待定位目標的位置進行快速響應，即快速解算出位置信息。當前，已有大量研究人員在該領域取得豐碩的研究成果。文獻[19]提出了一種基于AOA 的室內實時定位方法，該系統利用Wi-Fi 信號的多載波特性在天線和數據包較少的情況下快速估計信號的AOA，保證了定位的實時性。文獻[20]設計了一種利用智能天線的實時定位系統，該系統利用智能天線接收的信號強度進行定位，避免了離線階段密集型數據庫的建立，提高了效率。上述研究雖然保證了定位的實時性，但是定位精度都在米級，難以滿足愈發嚴苛的精度要求。文獻[21]提出了一種基于載波相位測量的高精度定位算法，該算法基于多個時間點的測量數據，可以對整周模糊度進行解算，進而實現高精度定位。該算法可以達到亞米級甚至厘米級的定位精度，前提是累積足夠數量采樣時間點的測量數據。對于實時定位中的應用場景，短時間內往往不能提供足夠多的測量數據，導致該算法在實際應用中存在局限性。因此，設計可以兼顧定位精度和解算速度的定位算法具有重要的現實意義。

基于上述考慮，本文提出了一種基于載波相位的高精度室內快速定位算法。

本文主要研究工作如下。

1)引入參考終端消除設備間鐘差對定位算法的影響。具體來說，結合移動終端及參考終端的測量值，利用TDOA 差分測量和載波相位雙差測量消除設備間鐘差的影響。

2)利用鎖相環（PLL,phase lock loop）不失鎖期間整周模糊度不變的特性，設計了一種結合多時間點測量數據的整周迭代解算算法，該算法可以加速整周模糊度的解算，進而縮短定位所需的時間。

3)在消除設備間鐘差和結合多時間點測量數據迭代解算整周模糊度的基礎上，提出了一種基于載波相位的高精度室內快速定位算法。

4)仿真結果表明，本文所提基于載波相位的高精度室內快速定位算法可以完全消除設備間鐘差對定位的影響，在短時間內精確解算整周模糊度，實現高精度的三維定位。當存在周跳殘余時，本文所提基于載波相位的高精度定位算法依然可以保持比較高的定位精度。

1 系統模型

1.1 定位場景

本文所提基于載波相位的高精度室內快速定位算法的定位場景設定在一個室內三維空間內，其中有M個位置已知的固定無線接入點，編號分別為1,2,…,M，位置坐標為ui=(xi,yi,zi)T，i=1,2,…,M。將編號為1 的無線接入點設為參考無線接入點，其他無線接入點分別結合其測量值來獲取相應的TDOA值。除了無線接入點外，三維空間內還有2 個終端，一個是移動終端s，位置未知，在t時刻的坐標為，可以在三維空間內隨機移動；另一個是參考終端r，位置已知且固定，坐標為u(r)=(x(r),y(r),z(r))T。假設在定位過程中，2 個終端始終可以與各個無線接入點進行直接通信。各個無線接入點可以接收2 個終端發射頻率為fc的C-PRS信號[13]，并觀測接收信號的TOA 值和載波相位值。

1.2 TDOA 測距模型

在t時刻，編號為i（i=1,2,…,M）的無線接入點收到移動終端s發射的連續信號并觀測得到TOA值為

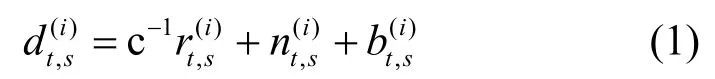
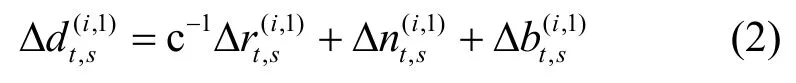
其中，Δ(·)(i,1)=(·)(i)-(·)(1)。同理，參考終端r的TDOA 觀測值可以表示為

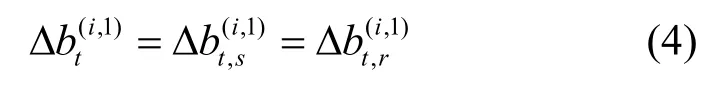
編號為2,3,…,M的無線接入點在t時刻分別結合參考無線接入點的測量值獲取相應的TDOA 觀測值。這里將它們統一表示成向量的形式

1.3 載波相位測量模型

載波相位測距常應用于GNSS 中，由于載波相位信號的周期性，信號接收機只能觀測到一個小于一個周期的相位φr，稱為相位的殘余部分，而相位的整數倍周期部分2πN未知，其中N為整周模糊度。真實的相位可以表示為

想要得到真實的相位，就需要精確地解算整周模糊度N。在觀測初期，信號接收機觀測到相位的殘余部分φr，同時鎖相環或者鎖頻環（FLL,frequency lock loop）對載波相位的跟蹤進行鎖定，隨著時間的變化，信號發射機和信號接收機之間的距離可能會發生變化，這意味著真實相位可能發生變化，只要鎖相環或者鎖頻環不失鎖，信號接收機在初期觀測的整周模糊度N就保持不變，真實相位的變化量體現在相位殘余部分[22]。移動終端s在t時刻觀測到來自編號為i的無線接入點的載波相位信號的相位可以表示為

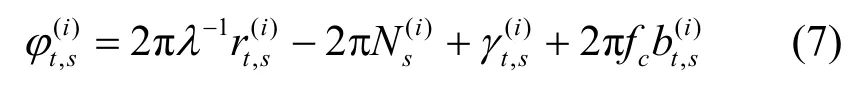
2 算法描述

2.1 消除鐘差

從式(2)和式(7)可以看出，TDOA 觀測值和載波相位觀測值都存在鐘差。為了消除設備間的鐘差對定位精度帶來的影響，本文所提基于載波相位的高精度定位算法引入了位置已知的固定參考終端r。對于TDOA 觀測值，考慮編號為1 的參考無線接入點、編號為i的無線接入點、移動終端s以及參考終端r，將式(2)和式(3)做差可得TDOA 差分測量值或TOA 雙差測量值

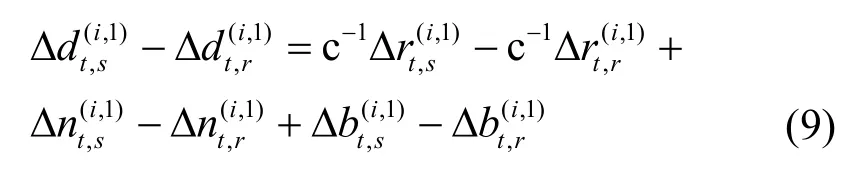
由于參考終端r的位置已知，因此為已知量。根據式(4)可知=0，將所有已知量移到等式左邊可得移動終端s消除鐘差之后的TDOA 觀測值為

對于載波相位觀測值，考慮編號為1 的參考無線接入點、編號為i的無線接入點、移動終端s，將做差可得載波相位單差測量值

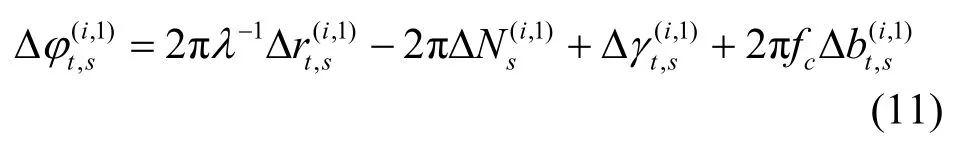
同理，對于參考終端r有載波相位單差測量值

將式(11)和式(12)做差可得載波相位雙差測量值

其中，Δ(·)s,r=(·)s-(·)r，，為4 次（2 個無線接入點分別觀測終端s和終端r的載波相位）載波相位測量誤差方差的和。與TOA 測量同理，在消除鐘差的同時引入了更大的測量方差。由于，因此=0，將已知量移到等式左邊可得雙差方程

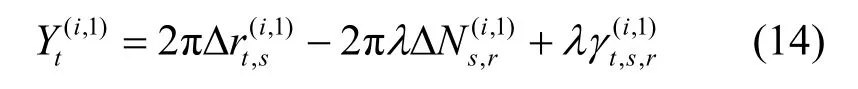
2.2 基于多時間點的整周迭代解算算法

載波相位測距比TDOA 測距具有更高的精度，那么應用載波相位測距得到的距離信息進行定位可以取得更高的定位精度。載波相位高精度測距的關鍵在于整周模糊度N的精確解算。觀察式(14)可知，除了未知的雙差整周模糊度和雙差測量誤差之外，還存在未知量，將展開可得

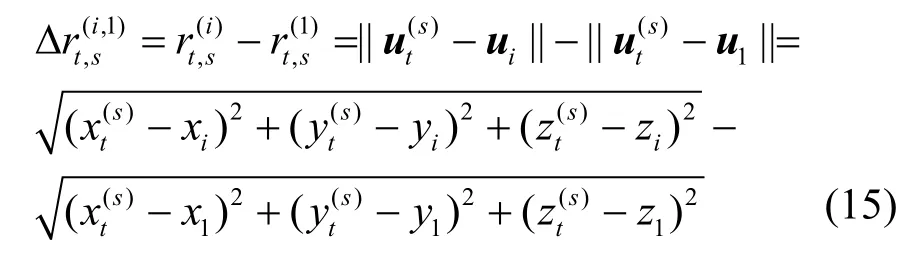
將TDOA 測距模型中觀測得到的TDOA 向量Δdt代入傳統的TDOA 定位算法（如Chan 算法[24]）得到一個t時刻關于移動終端s的粗定位結果ut,p。限于TDOA 的測距精度和三維定位場景，粗定位結果ut,p的定位精度往往不能達到很高的定位精度。

假設在第k-1 輪次迭代的結果為ut,k-1=(xt,k-1,yt,k-1,zt,k-1)T，將式(15)在ut,k-1上進行泰勒展開，從而達到線性化方程的目的，展開形式如下

將式(16)代入式(14)得到泰勒展開方程，并將i分別等于2,3,…,M得到的泰勒展開方程組成方程組，形式如下

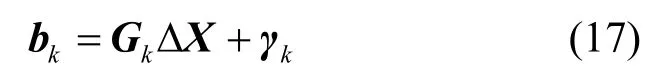
其中，bk=-2π(||ui-ut,k-1||-||u1-ut,k-1||)，Gk=[Ut,-λE(M-1)(M-1)]，Ut為泰勒展開系數矩陣，E(M-1)(M-1)是規模為M-1的單位矩陣，ΔX=[xt,k-xt,k-1,yt,k-yt,k-1,zt,k-zt,k-1,。

方程組(17)有唯一解的必要條件是方程數量≥未知數的數量。方程組(17)中的方程數量是M-1，未知數的數量為3+M-1，不滿足上述條件，所以方程組(17)顯然沒有唯一解。為了解決這一維度問題，假設鎖相環或者鎖頻環在n（n≥2）個時間點上不失鎖，即整周模糊度N保持不變，將n個時間點上（t,t+1,…,t+n-1）的雙差方程組成如式(17)所示的方程組，則方程組(17)中元素更新為，，Z是規模為（M-1）×3 的零矩陣，ΔX=[xt,k-xt,k-1,yt,k-yt,k-1,zt,k-zt,k-1,…,zt+n-1,k-zt+n-1,k-1,。運用加權最小二乘法求解方程組(17)可以得到

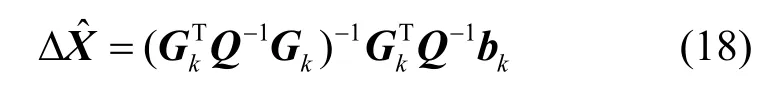
其中，Q為測量誤差的協方差矩陣。通過

可得第k輪迭代的結果uk，其中中前3n個元素組成的向量。將uk作為泰勒展開點繼續進行迭代，以此類推，直至解算結果收斂。本文所提基于多時間點的整周迭代解算算法流程如圖1所示。

圖1 整周迭代解算算法流程

2.3 最終定位

當解算出整周模糊度的浮動解后再利用LAMBDA（least-square ambiguity decorrelation adjustment method）算法[25]求得整周模糊度的固定解。這里的整周模糊度固定解為雙差整周模糊度，按照式(20)可以修正相位差并計算出距離差。

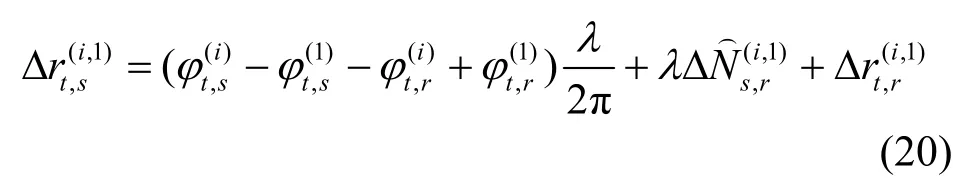
將距離差代入傳統TDOA 定位算法即可解算出最終的位置估計uf。

3 仿真分析

仿真定位場景設定在一個三維空間內，如圖2 所示。三維空間的長L=100 m，寬W=20 m，高H=10 m，參考終端r位置已知且固定于房間正中間，移動終端s可以在房間內隨機移動，2 個終端始終在各個無線接入點的通信范圍內，所有無線接入點及參考終端的坐標均在圖2 中標出。在仿真中，所用信號載頻fc為3.5 GHz，無線接入點數量M=6，光速c=3×108m/s。

圖2 仿真場景

3.1 一般場景下算法性能仿真分析

為了驗證所提算法對整周模糊度解算的加速效果，仿真實驗分為兩部分：該算法與自身的對比實驗以及該算法與現有相關算法的對比實驗。

在與自身的對比實驗中，相同的仿真場景下，設置迭代組和非迭代組的對比實驗來驗證本文所提基于多時間點的整周迭代解算算法對整周模糊度解算的加速效果。兩組實驗分別在不同數量的采樣時間點上進行多次位置估計，并計算位置估計的均方根誤差來量化定位精度。兩組實驗的流程除整周模糊度的解算部分不同外，其余均相同。針對整周模糊度解算部分，迭代組采用本文所提基于多時間點的整周迭代解算算法解算整周模糊度浮動解，而非迭代組只使用方程組(17)一次解算的結果作為整周模糊度的估計值，即方程組(17)在代入初始迭代點ut,0（ut,0為傳統TDOA 算法估計的位置）之后進行一次解算的結果中的整周模糊度部分作為整周模糊度浮動解。不同采樣時間點數上算法的性能如圖3 所示，從迭代組的仿真曲線可以看出，當采樣時間點數n取不同值時，本文所提基于載波相位的高精度定位算法的性能不同。隨著n的增大，位置估計的均方根誤差變小，算法的定位精度變高，注意，這里n需不小于4，這是因為當無線接入點數量M=6，采樣時間點數n＜4 時，方程組(17)為欠定方程組或者迭代結果無法收斂，鑒于相關算法在采樣時間點數n=4 時均方根誤差的仿真結果大概在幾十米量級，為了更好地展示對比效果，圖3 從采樣時間點數n=5 開始。通過對比迭代組和非迭代組的曲線可以看出，在相同測量標準差下，迭代組在采樣時間點n=5 時位置估計的均方根誤差小于非迭代組在采樣時間點n=50 時位置估計的均方根誤差。本文所提算法相對于非迭代的解算算法在達到更好的精度效果時可以使用更少采樣時間點的測量數據，這說明本文所提算法可以加速整周模糊度的解算，進而縮短定位所需時間。

圖3 不同采樣時間點數上算法的性能

在與現有相關算法的對比實驗中，相同仿真場景下，與文獻[21]中所提算法進行對比。分別在不同數量的采樣時間點上進行多次位置估計，并計算位置估計的均方根誤差來量化定位精度。仿真結果如圖3 所示，通過對比迭代組和相關算法的曲線可以看出，在相同測量標準差下，迭代組在采樣時間點數n=10 時位置估計的均方根誤差和相關算法在采樣時間點數n=50 時位置估計的均方根誤差相當。在達到相同的定位精度性能的同時，本文所提算法相對于現有相關算法可以使用更少采樣時間點的測量數據，這說明本文所提基于載波相位的高精度室內快速定位算法可以在短時間內實現高精度定位。

圖4 為不同誤差標準差下的整周模糊度收斂情況。仿真中，采樣時間點數n=4，誤差標準差分別取不同值，整周模糊度殘差由計算。

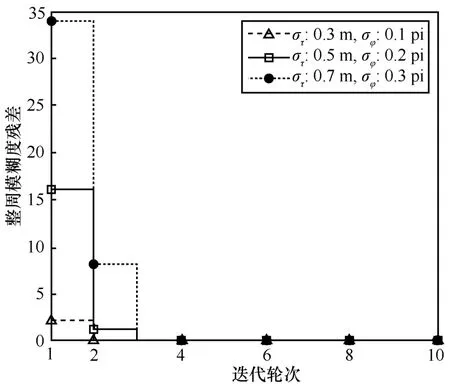
圖4 不同誤差標準差下的整周模糊度收斂情況

如圖4 所示，本文所提基于多時間點的整周迭代解算算法的整周模糊度解算結果在不同的誤差標準差下均能收斂。為了證明本文所提算法的整周模糊度解算結果在不同采樣時間點上均能收斂，表1 統計了不同誤差標準差及不同采樣時間點下本文所提算法解算結果收斂所需迭代輪次，將算法分別仿真1 000 次，求得迭代輪次后進行求和平均。從表1 中可以看出，在不同的仿真場景下，本文所提基于多時間點的整周迭代解算算法的整周模糊度解算結果均能在4 次以內得到收斂。

表1 不同誤差標準差和不同采樣時間點下所需平均迭代輪次

除了采樣時間點數n之外，TOA 距離標準差和載波相位測量標準差也是影響算法性能的重要因素。固定采樣時間點數n，分別分析不同的TOA距離標準差和不同的載波相位測量標準差對本文所提基于載波相位的高精度定位算法的整體性能的影響。圖5 為不同誤差標準差下所提算法的位置估計的性能對比。從圖5 中可以看出，當載波相位測量標準差不變時，僅改變TOA 距離標準差，3 條累積概率分布曲線幾乎重合為一條線。因為TOA 距離標準差只會影響迭代算法初始點的精度，隨著迭代算法的進行，迭代的結果將會收斂于真實值，對整周模糊度浮動解的解算影響不大。而當TOA 距離標準差不變時，隨著載波相位測量標準差的增大，算法精度性能下降，這是因為載波相位測量誤差量存在于方程組中，不能在迭代過程中消除或者減小其影響。

圖5 不同誤差標準差下所提算法的位置估計的性能對比

為了驗證本文提出的鐘差消除方法對鐘差的消除效果，將本文所提基于載波相位的高精度定位算法在無線接入點間存在鐘差和無線接入點間完美同步2 種情景下分別仿真并進行定位精度性能對比。假設設備之間的鐘差在0～50 ns上均勻分布，仿真結果如圖6 所示，從圖6 中可以看出，當測量標準差一定時，2 種情景下絕對誤差的累積概率分布曲線重合，當測量標準差不同時，2 種情景下絕對誤差的累積概率分布曲線均重合。這說明在不同的測量標準差條件下通過引入參考終端都可以完全消除設備間鐘差對定位精度的影響。

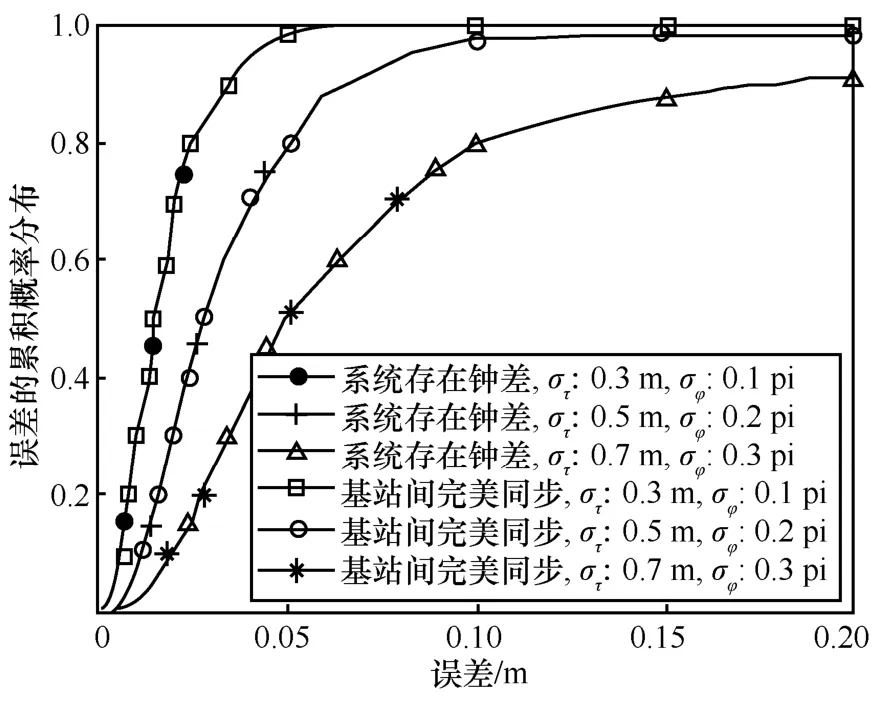
圖6 有無鐘差條件的所提算法的性能對比

圖7 為本文所提基于載波相位的高精度定位算法與傳統TDOA 定位算法的性能對比。如圖7所示，在相同的TDOA 測量標準差下，所提算法的定位誤差有90%的概率在0.07 m 內，而傳統TDOA 定位算法的定位誤差則在3.56 m 內，前者顯著優于后者2 個數量級。當減小傳統TDOA 定位算法的測量標準差時，所提算法仍然優于傳統TDOA 定位算法。這說明本文所提基于載波相位的高精度定位算法相比于傳統定位算法具有很高的定位精度優勢。

圖7 所提算法與傳統TDOA 定位算法的性能對比

3.2 考慮周跳殘余場景下性能仿真分析

在獲取載波相位觀測值時，無線接入點需要始終保持對載波相位參考信號的跟蹤。由于室內信號傳播環境比較復雜，多徑效應、物體的遮擋以及信號的干擾都可能使接收信號產生短暫中斷，從而導致觀測相位的整周數產生跳變，上述現象稱為周跳。周跳發生后，無線接入點可以恢復對載波相位定位參考信號的跟蹤觀測，使觀測結果中相位的小數部分不受影響，但是整數部分發生跳變，從而導致載波相位的整體觀測結果發生錯誤。在連續觀測載波相位的系統中，周跳不僅會影響當前時刻的載波相位觀測值，同樣將影響該時刻之后的載波相位觀測值。

在基于載波相位的高精度定位算法中，周跳往往是影響定位精度的一個重要因素，因此，周跳的檢測與修復是十分必要的。在現有的研究中，很多周跳檢測與修復算法[26-30]已經被提出。本文所提基于多時間點的整周迭代解算算法可以利用現有的周跳檢測與修復算法對周跳進行處理。例如，利用多個采樣時間點上的載波相位觀測值的高次差[30]可以實現周跳的檢測與修復，即確定周跳發生的時刻以及估計周跳的大小并對整周部分進行補償。但由于虛警概率的存在，現有的周跳檢測與修復算法有時不能完美修復周跳，偶爾存在少量的周跳殘余，即未完美修復的周跳以及未檢測到的周跳。

下面給出存在周跳殘余情況下本文所提基于載波相位的高精度定位算法的仿真，以驗證存在周跳殘余下該算法的性能。參照文獻[25-28]中的關于周跳殘余的描述，假設在50 個采樣時間點上隨機2 個采樣時刻存在周跳殘余，周跳殘余大小在[-5,+5]中的非零整數離散值上均勻分布，TOA 距離標準差為0.5 m，載波相位測量標準差為0.2 pi。圖8 為采樣時間點分別取25 和45 下，是否存在周跳殘余下所提算法位置估計的性能對比。

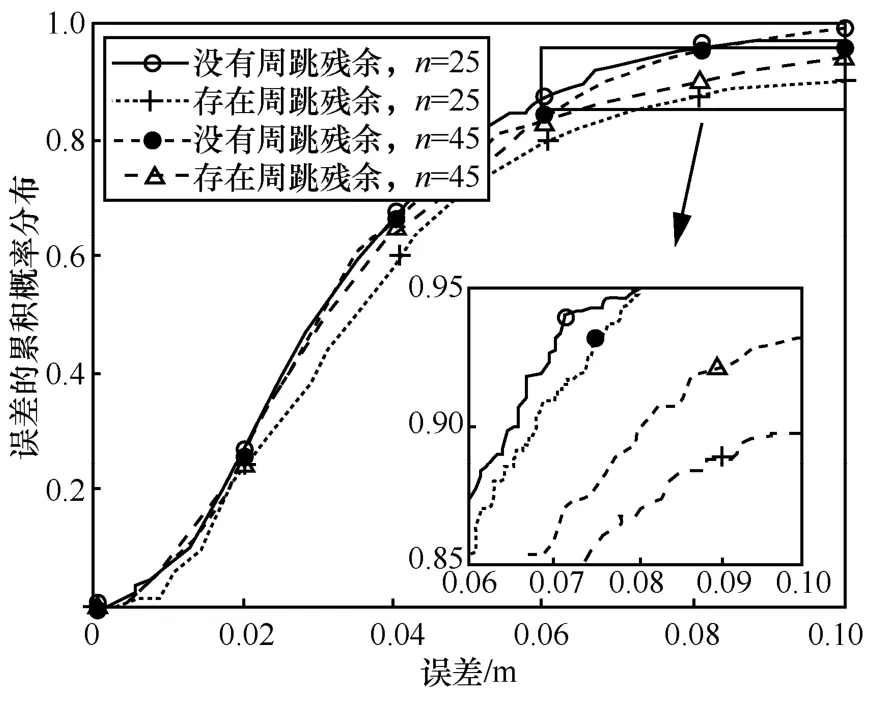
圖8 是否存在周跳下所提算法位置估計的性能對比

圖9 為是否存在周跳對不同采樣時間點上算法性能的影響。從圖9 中可以看出，存在周跳殘余和沒有周跳殘余下所提算法的CDF 曲線非常接近，這說明本文所提算法在存在周跳殘余的情況下依然能保持很高的定位精度。在圖9 中，周跳殘余存在于隨機的2 個采樣時刻，存在周跳殘余下本文所提算法位置估計的RMSE 在某些采樣時間點上相對于沒有周跳殘余下算法的RMSE 略有升高，但是依然保持良好的定位性能。

圖9 是否存在周跳對不同采樣時間點上算法性能的影響

4 結束語

本文分析了室內無線環境影響定位算法的因素，提出一種基于載波相位的高精度室內快速定位算法。考慮到設備間的鐘差會降低定位算法的定位精度，該算法通過引入參考終端，利用載波相位的雙差測量值來消除鐘差的影響。考慮到鎖相環不失鎖整周模糊度不變的特性，設計了一種解算整周模糊度的迭代算法。此外，分析了周跳對本文所提算法的影響。仿真結果表明，該算法可以完全消除鐘差的影響，并在短時間內精確解算整周模糊度，實現厘米級的三維定位。