修正的R-S水泥漿流變模式及其評價
盧勁鍇
(同濟大學土木工程學院, 上海 200092)
0 引言
注漿工藝在幾十年前就已經大規模用于工程實踐之中,注漿理論是注漿工程設計與評價的重要依據,其中漿液的擴散距離是一個重要的指標。現在大多數的注漿理論都是建立在漿液為牛頓流體,且服從穩定滲流的基礎上,而真實注漿過程則具有明顯的非穩定特性,注漿漿液也具有很強的非牛頓流體特性[1],漿液的擴散受漿液的動切力、塑性粘度和水化程度的流變特性影響較大[2]。漿液的流變特性與漿液的水化程度、水泥漿體凝聚結構形成和發展密切相關[3]。因此,研究注漿材料的流變性顯得尤為重要。
本文從水泥凈漿入手,圍繞其流變模式進行探究和討論,提出了一種新型的流變模式——修正R-S模式,以便為今后的工程實踐提供理論參考。
1 描述水泥漿液流變特性的常見模式
1.1 流變模式的評價標準
水泥漿的空間網狀結構在靜置時凝聚加強,受到剪切力作用則被打散,若剪切速率固定,又能形成一種新的空間結構狀態。適用于水泥漿的流變方程應該能夠反映水泥漿的三點特性:
(1)水泥漿流變方程應體現水泥漿液的靜切力0,這決定著低剪切速率區域流變方程的準確性。
(2)當剪切速率趨近于正無窮時,水泥漿空間網狀結構的形成速率與破壞速率相等,水泥漿粘度應趨近于某一定值,即極限粘度∞。
(3)當剪切速率為0+ 時,其粘度也應是某一個定值(初始粘度),而不是無窮大。
除了要滿足上述三點特性以外,流變方程還應該具有曲線形狀控制參數和參數物理意義明確等優點。
1.2 常見流變模式及局限性
用來描述剪切速率與剪切應力之間函數關系的關系式,稱為流體的流變方程或流變模式[4]。非牛頓流體的流變方程主要有:賓漢模式[5]、冪律模式[6]、H-B模式(赫巴模式)[7]、卡森模式[8]、R-S模式(羅伯遜-史蒂夫模式)[9]、雙曲模式[10]、Sisko模式[11]、GHB模式[12]、L-M模式[13]、基于Sisko的四參數模式[14]、多項式模式[13]。
在雙參數的流變模式的局限性主要有:賓漢模式的屈服應力是一個計算值,一般高于水泥漿的實際屈服應力;冪律模式中并沒有反映屈服應力的參數,描述低水灰比的水泥漿時誤差很大;卡森模式描述水泥漿的能力不突出,還存在參數物理意義不明確的缺點。在三參數流變模式中,H-B模式不能反映卡森流體的流變特性,且當剪切速率無限增大時不存在極限粘度,不符合大多數非牛頓流體的實際情況[12]。Sisko模式不具有靜切力,不能很好地反映水泥漿具有空間網狀結構的物理特性;雙曲模式和R-S模式在剪切速率趨向無窮大時,不存在極限粘度;GHB模式表達式過于復雜,計算困難;Ⅰ型多項式模式在剪切速率無窮大時,粘度為無窮大,不符合實際;Ⅱ型多項式模式的參數物理意義不明確等。因此,尋找一種適用于水泥漿的三參數流變模式十分必要。
2 修正R-S模式的提出
綜合考慮以上要求,提出一種新的適用于水泥漿液的流變模式:修正R-S模式。

其中:0為屈服值;為控制系數;∞為極限粘度。
修正R-S模式的粘度表達式為:

當 =0時,=0,即符合水泥漿液具有靜切力的物理特性;由于水泥漿具有剪切稀釋性,屬于假塑性流體,m∈(0,1),則當 →∞時,→∞,即符合水泥漿存在極限粘度的情況;當 =0時,=0+即初始粘度是由屈服值與控制系數的乘積和極限粘度兩部分構成,是一個有限的定值。其中,初始粘度可以理解為空間網狀結構凝聚提供的粘度與水泥顆粒與分散介質間的內摩擦之和。屈服值與控制系數的乘積表示空間網狀結構凝聚提供的粘度;極限粘度表示水泥顆粒與分散介質間的內摩擦。
3 基于實驗的流變模式對比分析
將實測數據用賓漢、冪律、H-B、卡森和修正R-S模式分別進行回歸,得到回歸系數2和均方誤差MSE。圖1反映了常見流變模式的回歸系數隨水灰比的變化情況。賓漢模式在[0.7,1.5]的中水灰比區間對水泥漿流變性能的描述能力較強,但在[0.45,0.6]的低水灰比區間(濃漿)和[1.5,2]的高水灰比區間(稀漿)的回歸系數2都有所下降,說明賓漢模式在濃漿和稀漿中的表現較差,描述能力不穩定。
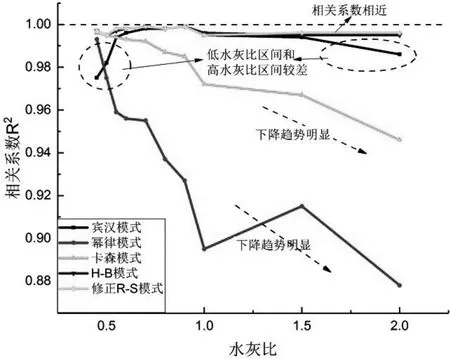
圖1 常見流變模式相關系數隨水灰比變化曲線
H-B模式和修正R-S模式的回歸系數2始終維持在較高的水平,說明二者無論對濃漿還是稀漿都有較為優秀且穩定的描述能力,在水灰比大于1.0時,二者的相關系數都有一個輕微的下降,但水灰比更大時,二者的相關系數在保持穩定的基礎上仍有輕微增加,可見H-B模式和修正R-S模式對水泥漿流變性的描述能力都非常好。
濃漿實測點有較明顯的下彎趨勢,這是由于濃漿具有較強的觸變性造成的。而賓漢模式是一條直線,從實測點中穿過,可見誤差較大;冪律模式則彎曲過度,也不能很好地擬合實測數據點,描述能力較差。卡森模式、H-B模式和修正R-S模式在水灰比為0.5的濃漿中擬合效果較好(見圖2)。
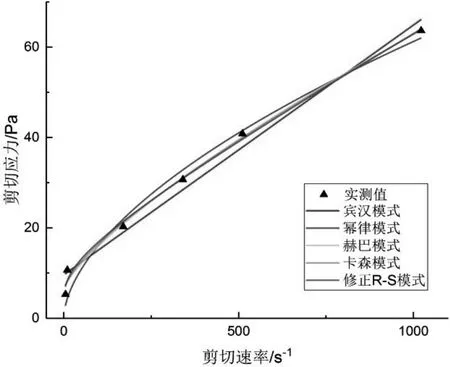
圖2 水灰比0.5的常見流變模式回歸曲線
盡管在某一特定水灰比下的效果不一定最好,但綜合全部水灰比來看,修正R-S模式和赫巴模式回歸系數最接近1、均方誤差最小,描述能力和回歸效果最好,其次分別是賓漢模式、卡森模式和冪律模式。綜合來看,修正R-S模式在雙參數和三參數的常見流變模式中表現更優秀,相對四參數模型來說也更簡潔。
4 結束語
在分析水泥漿流變特性和常見流變模式局限性的基礎上,提出了修正R-S模式。修正R-S模式參數物理意義明確、適用濃度范圍廣,優勢突出。

