融合改進天牛須搜索的教與學優化算法
歐陽城添,周 凱
江西理工大學 信息工程學院,江西 贛州341000
教與學優化(teaching-learning based optimization,TLBO)算法[1]是印度學者Rao 等人于2011 年提出的一種模擬班級教學過程的群智能算法。將優化問題的解空間描述為一個班級,班級里的每個學生對應于解空間的各個解,其學習成績對應于解的適應度值,教師則代表當前適應度值最好的解。該算法原理簡單,參數較少,收斂速度較快,已被成功應用于多個學術或工業領域,如神經網絡的參數優化[2]、視覺跟蹤[3]、數據分類[4]、PID控制[5]等。
然而,在面對維度較高的復雜優化問題時,標準TLBO 算法往往無法收斂到全局最優,存在易早熟、解精度低、陷入局部最優等問題。因為標準TLBO算法種群個體采用隨機初始化產生,在初始種群沒有覆蓋到全局最優解的情況下,如果在有限迭代次數內無法搜索到最優解,那么算法早熟是難以避免的。求解單峰問題時,若最優解所在區域種群個體適應度值相差較大,或最優個體和次優個體的適應度相差較小,則算法容易提前收斂。求解多峰問題時,若解與解之間相距較遠,則無法保證種群覆蓋到所有最優區域,這時算法也容易提前收斂。此外,迭代過程中學生個體在教學階段會向教師所在區域靠近,雖然有利于算法快速收斂,但是當前最優不一定是全局最優,持續的迭代會使學生個體高度聚集,將導致算法陷入局部最優。
為提高算法求解性能,近年來不少專家學者對標準TLBO 算法進行了改進研究。Rao 等人[6]引入精英策略和變異機制,提出精英教與學優化(elitist teachinglearning based optimization,ETLBO)算法,能有效提高學生整體學習水平,有利于算法快速收斂,但容易收斂到局部極值。于坤杰等[7]在ETLBO 算法的基礎上引入反饋機制,增加差生與老師之間的反饋交流,提出一種基于反饋的精英教與學優化(Feedback ETLBO,FETLBO)算法,實驗證明該算法可以有效抑制種群的過早收斂,然而也存在求解精度不高的問題。童楠等[8]提出一種基于反思機制的教與學優化(teaching-learning based optimization based on reflection,RTLBO)算法,利用高斯正態分布和教師與學生之間的差異實現兩者各自的局部搜索,達到同步提高的目的,實驗表明該改進算法具有穩定的魯棒性,但在多峰高維測試函數上,收斂精度明顯下降。李麗榮等[9]提出具有動態自適應學習機制的教與學優化(teaching-learning based optimization with dynamic self-adapting learning,DSTLBO)算法,在教學階段加入非線性的動態學習因子和動態隨機搜索策略,有效提高了收斂速度和解精度,但依然存在過早收斂的現象。王培崇等[10]提出一種融合加權中心學習的教與學優化(teaching-learning based optimization with weighted center,WCTLBO)算法,以加權中心取代教師個體,在學習階段引入小組討論,有效避免種群陷入局部最優,但收斂精度一般。
針對標準TLBO 算法的問題和以上改進算法的不足,本文提出融合改進天牛須搜索的教與學優化(teachinglearning based optimization with improved beetle antennae search,BASTLBO)算法。該算法進行了三方面的改進:首先,針對種群隨機初始化,多樣性無法保證的問題,提出Tent 映射反向學習策略,使初始種群在解空間分布得更加均勻,盡可能覆蓋到全局最優解,有利于算法快速收斂而又避免早熟;其次,在教學階段,先對教師個體執行二次插值天牛須搜索,然后再讓學生向老師學習,進行自我更新,以此來提高算法全局尋優和對當前最優解區域進行精細搜索的能力;最后,由于教學階段會引導種群向最優個體所在空間收斂,為保證算法在陷入局部最優時能迅速跳出,提出自適應混合變異策略,結合柯西變異和高斯變異自身特性,使算法達到全局開發與局部搜索的動態平衡。
1 標準TLBO算法
TLBO 算法的原理是利用教師和班級平均學習水平之間的差異性來引導學生進化學習,之后學生之間也要相互學習,進而提高整個班級的成績。具體過程分為教學和學習兩個階段。
1.1 教學階段
教學過程的數學描述如式(1)所示。
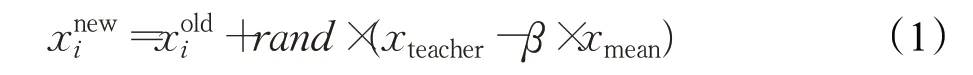
1.2 學習階段
學生xi與另一名隨機選擇的學生xj相互學習,比較其對應的目標函數值f(xi)和f(xj),讓學習差的向學習好的進行學習,即:
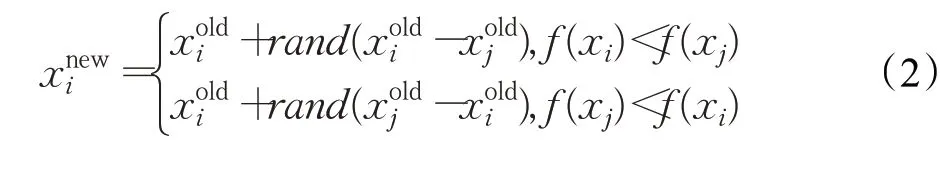
2 融合改進天牛須搜索的教與學優化算法
2.1 種群初始化策略
為了增強種群的多樣性,在BASTLBO 算法中,首先使用Tent映射產生混沌初始種群,然后通過反向學習產生反向種群,最后對混沌初始種群及其反向種群進行排序,從中選擇適應度值較優的解組成初始種群。
Tent映射產生混沌粒子序列的公式定義如下:

式中,表示第t次迭代粒子i在第d維分量上的混沌變量,t=1,2,…,T,d=1,2,…,D。
通過式(3)迭代T次可以得到t個混沌變量Yt=(Yt,1,Yt,2,…,Yt,D)組成的混沌序列,再經過式(4)進行逆映射,即可得到t個初始解Xt=(Xt,1,Xt,2,…,Xt,D),記為種群X。
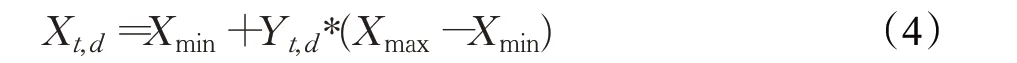
其中,Xmax和Xmin來自搜索空間的取值范圍[Xmin,Xmax]。
作為一種提高隨機搜索算法搜索能力的有效方法,反向學習(opposition-based learning,OBL)策略的原理[11]是若在D維空間中存在一個點x=(x1,x2,…,xD),xi∈[ai,bi]則其反向點為,其中,i∈[1,D]。因此由種群X計算反向種群OX:

將種群X和反向種群OX合并得到新種群,即Xnew={X?OX},然后計算Xnew的目標函數值并排序,若是極小值尋優,則從小到大排序,若是極大值尋優,則從大到小排序,然后選取其中適應度值最好的前N個個體作為初始種群。
2.2 改進天牛須搜索
TLBO 算法有一個明顯的缺點是教師個體缺少學習機制,即教師沒有進一步地尋優,沒有對所在的空間進行精細的局部搜索。而天牛須搜索(beetle antennae search,BAS)算法[12]不同于其他優化算法,它恰好只需要一個個體,不需要知道函數具體形式和梯度信息即可實現高效尋優,運算量小,尋優速度快。BAS 算法流程如下:
(1)因為天牛頭的朝向隨機,所以天牛左須指向右須的向量表示為:

其中,rands(k,1)表示生成k維的隨機向量。
(2)設置天牛步長δ,以線性方式進行遞減,t為當前迭代次數,則第t次迭代時天牛的移動步長為:

式中,eta_δ為步長遞減系數。
(3)設置天牛兩須距離d,同樣以線性方式遞減,其遞減系數為eta_d,第t次迭代時兩須的距離為:

(4)天牛左右兩須進行位置更新:

式中,左須xl、右須xr都是k維向量,xt表示第t次迭代時天牛質心的位置。
(5)計算左右兩須xl和xr的適應度值f(xl) 和f(xr),根據二者大小關系,判斷天牛的前進方向:

其中,sign 為符號函數。
(6)計算天牛移動后的適應度值。
(7)判斷是否符合迭代結束條件,符合就結束迭代,否則重復(1)到(6)直到符合條件。
雖然BAS算法原理簡單,收斂速度快,但是單個天牛在高維空間中的尋優能力還是有所欠缺,容易陷入局部最優,有必要對其進行改進。因此,引入二次插值算子:
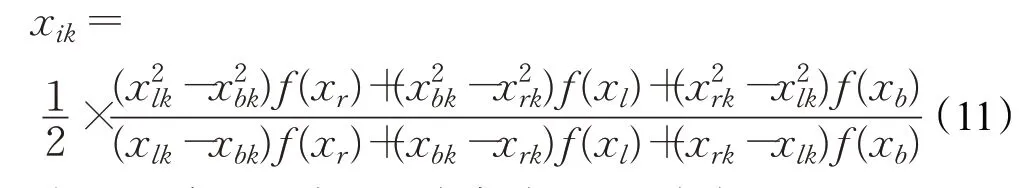
其中,k表示維度,xb為當前全局最優解。
采用二次擬合函數法,在每一次天牛位置更新時,都可以利用二次插值得到一個異于當前解xt的新解xi,對比它們的適應度值,若f(xi) 改進BAS 算法雖然高維尋優能力有所增強,但是該算法搜索到的最優點不一定是全局最優點。因此要給BAS 設置兩個終止條件來保證算法整體搜索效率:第一個是解的精度;考慮到在某些問題的求解過程中,精度要求即使較低,BAS 算法可能也會迭代很多次,因此第二個是要設定固定的迭代次數。當精度達到要求或迭代次數達到設定值,則搜索完畢,直接應用所得到的點替換教師個體。 由高斯變異、柯西變異自身的概率分布特性以及在其他優化算法中的應用效果可知,高斯變異可以賦予算法更好的局部搜索能力,柯西變異則具有較強的全局探索能力,因此可以結合二者特性,通過混合變異使教與學優化算法能夠自適應調節學生之間互相學習的效果。在學生個體更新公式中引入服從混合變異分布的隨機向量,如式(12)所示。 在算法迭代過程中,前期需要更強的局部搜索能力,使算法能夠快速地收斂到全局最優附近,節省算法尋優時間。而后期為了使TLBO逃脫局部極值的束縛,避免早熟收斂,則需要加強算法的全局探索能力,因此TLBO 算法前期要側重高斯變異,后期要側重柯西變異。α(t)與γ(t)隨迭代進程計算如下: 其中,t是當前迭代次數,T是算法最大迭代次數,G(0,1)為標準高斯分布,C(0,1)為柯西分布。 步驟1以個體X0(0)為起點,依據式(3)、(4)進行迭代得到混沌種群X,種群X通過式(5)迭代得其反向種群OX。令Xnew={X?OX},計算Xnew的目標函數值并排序,選取其中適應度值最好的前N個個體組成初始種群POP(0)。 步驟2計算適應度值,選出最佳個體,設為教師xteacher,并計算班級平均值xmean。 步驟3對教師個體xteacher執行天牛須搜索。設置改進BAS 算法相關初始參數,迭代次數t=0,依據式(10)、(11)進行天牛迭代,判斷是否滿足BAS算法終止條件,若是,則進入下一步,否則繼續迭代。 步驟4更新教師個體xteacher=xt。 步驟5依據式(1)進行教師的“教”行為。 步驟6依據式(12)、(13)、(14)進行學生的相互“學”行為。 步驟7BASTLBO算法滿足結束條件,則輸出最優解Xgbest,結束算法,否則返回步驟2。 為了檢驗本文改進算法的尋優能力,選取6個經典benchmark 測試函數進行仿真實驗,分別是f1:Sphere、f2:Rosenbrock、f3:Schwefel2.22、f4:Rastrigin、f5:Griewank、f6:Ackley,它們的理論最優值均為0。其中f1到f3是單峰函數,可以測試算法收斂速度與精度,f4到f6是多峰函數,可以測試算法逃出局部極值的能力。表1給出了標準測試函數的具體信息,包括表達式和取值范圍。 表1 標準測試函數Table 1 Benchmark functions 此外,本文所有實驗運行環境始終一致,均在AMD A10-7300 處理器、Windows 10 操作系統下基于軟件Matlab2016a實現。 2.2 節中在原始天牛須搜索算法的基礎上引入二次插值算子,目的是得到尋優性能更好的BAS,然后將其嵌入到TLBO算法中。為了驗證二次插值的改進效果,設計實驗如下。 首先通過單因素實驗、正交分析確定BAS 的內部最優參數:初始步長δ0取1,兩須初始距離d0取2,步長和兩須距離的遞減系數均取0.95。然后通過3.1節中的標準測試函數對改進BAS和原始BAS進行優化性能比較。實驗條件為函數維度30 維,最大迭代次數1 000次。算法對不同函數均獨立運行30 次,結果取平均值并計算方差。對比數據如表2所示。 從表2可以看出,改進天牛須搜索的收斂精度和穩定性較原始算法有明顯提升。其中在30次的函數測試中,改進BAS 對多峰函數f4都成功收斂到了理論最優值0,方差也為0,同時在多峰函數f6上方差為0,說明改進算法具有較高的穩定性,驗證了引入二次插值算子的改進BAS的尋優有效性。 表2 原始BAS和改進BAS函數測試結果Table 2 Functional test results of original BAS and improved BAS 通過以上實驗可以確定改進BAS的可行性與優越性以及此種算法特有的內部參數值,為后續將其嵌入到TLBO 算法中提供了理論依據。然而為了保證本文實驗的嚴謹性,根據2.2節中的分析,還需要考慮固定迭代次數的設置問題,如果固定迭代次數過大,則會影響改進TLBO 算法的整體收斂效率,如果過小,則可能體現不出改進優勢。因此針對上述改進BAS,將最大迭代次數分別取200、1 000、2 000,在標準測試函數上進行獨立30次優化實驗,計算并統計最優解和均值,如表3所示。 表3 最大迭代次數對改進BAS優化性能影響Table 3 Effect of maximum iterations on improved BAS optimization performance 由表3可知,最大迭代次數對天牛須搜索算法的影響不大,因此為了保證BASTLBO改進算法的整體尋優效率,后續實驗中在給改進BAS設置終止條件時,固定迭代次數取值為200。 將僅使用Tent映射反向學習初始化策略的TLBO_1、僅加入改進天牛須搜索的TLBO_2、僅加入組合變異的TLBO_3 與標準TLBO 算法進行比較,探討本文每部分改進對算法整體效果影響,驗證不同策略的改進有效性。TLBO_2中加入的改進BAS內部參數設置同3.2節一樣,并且設置其迭代終止條件為固定搜索精度0.001,固定迭代次數200次。統一實驗條件,各算法種群規模為20,測試函數維度均為30維,最大迭代次數1 000次。獨立運行30次,統計各算法的解平均值和方差,結果如表4所示。 表4 不同改進策略結果比較Table 4 Comparison of results of different improvement strategies 結合表4數據,分析每種改進策略,TLBO_2對于單峰函數f3和多峰函數f4、f5,都可以收斂到函數最優值0,雖然在f1和f6上沒有尋到理論最優,但也是表現最優秀的。因為TLBO 算法的核心便是利用教師與學生之間的差異來尋優,始終讓當前最優個體指導整個種群進化,而加入了改進BAS的TLBO_2可以在算法每次迭代過程中獲得更優秀的當前最優個體,一方面提高了尋優精度,一方面使得種群在算法初始階段快速向可能最優解區域靠近,加快了收斂速度。實驗證明了在TLBO中引入改進天牛須搜索的有效性和優越性。在函數f2上,三種改進策略相比標準TLBO提升效果不是特別明顯,但TLBO_3表現最優,并且在f4上找到了理論最優值,在f5中方差為0,穩定性良好。這是因為TLBO_3中的組合變異策略有效增強了算法前期的局部勘探能力和后期的全局開發能力,實驗說明此策略對本文改進算法性能提升具有顯著影響。另外,使用了本文Tent映射反向學習策略的TLBO_1 相比于標準TLBO 算法優化性能也有一定提升。下文將繼續通過實驗測試融合了以上三種改進策略的BASTLBO算法的尋優性能。 將本文所提出的BASTLBO 算法與標準TLBO 以及兩種典型TLBO 改進算法FETLBO[7]、DSTLBO[9]進行對比,分別在維度為30 維、100 維的條件下,在3.1 節中的標準測試函數上進行尋優測試,參數設置同3.2 節一樣,FETLBO和DSTLBO的實驗參數參考各自文獻。獨立運行30次,計算并統計結果如表5所示。 從表5數據可以看出,函數維度為30維時,BASTLBO算法可以成功找到單峰函數f1的最優解,而參與對比的TLBO、FETLBO、DSTLBO算法雖然無法搜索到全局最優值,但FETLBO、DSTLBO 的性能較于TLBO 仍有較大提升。四個算法在f2上都沒有找到最優解,但觀察各算法的解均值和方差,可以看出BASTLBO表現最優。f3也是單峰函數,多峰函數f4極值點較多,但三種改進TLBO 算法均收斂到了全局最優。對于多峰函數f5,TLBO 算法解精度較低,而FETLBO、DSTLBO、 表5 不同維度下算法尋優結果對比Table 5 Comparison of algorithm optimization results in different dimensions 如圖1 所示,繪制出了30 維度下TLBO、FETLBO、DSTLBO、BASTLBO 算法在不同函數上的平均收斂曲線,結合表5 數據,進一步評估算法尋優性能。可以看出,在六個測試函數上,三種改進算法的解精度和收斂速度較標準TLBO 均有所提高,在f3上DSTLBO 前期收斂速度比BASTLBO 要快,除此之外,本文所提出的BASTLBO 算法無論在單峰還是多峰函數上始終都保持著較高的穩定性和尋優精度,且收斂速度最快,在其他算法陷入局部最優時,依然可以持續尋優。綜上,加入了本文提出的三種改進策略的BASTLBO 算法的綜合優化性能得到了有效驗證。 圖1 30維度下不同函數平均收斂曲線Fig.1 Average convergence curves of different functions in 30 dimensions 為了更好地評估BASTLBO算法的尋優能力,選取CEC2013 函數集中的10 個基準函數進行仿真實驗,具體函數信息如表6 所示,包括函數名稱、搜索空間范圍BASTLBO算法在本實驗中均成功收斂30次。在f6中,DSTLBO 表現最優,BASTLBO 與FETLBO 算法求解精度相當,但就方差而言,BASTLBO算法顯得更穩定些。 表6 CEC2013函數(部分)Table 6 CEC2013 functions(part) 當測試函數維度增加到100維時,四個算法均沒有在1 000 次迭代內找到函數f1的全局最優值,但是BASTLBO 算法的解精度要優于其他三種算法。對于f3、f4,BASTLBO均成功收斂30次,而FETLBO、DSTLBO在f4上表現相當,在f3上可以收斂到理論最優。三種改進TLBO 算法在30 維時可以找到f5函數的最優值,但在100維度時,尋優精度和穩定性均有不同程度的下降,而且可以注意到,此時DSTLBO、BASTLBO 還要稍遜于FETLBO 算法。在f6函數上,BASTLBO 算法100維下的求解精度較30 維時幾乎沒有下降,而FETLBO、DSTLBO均有所下降,說明本文改進算法具有更好的魯棒性,適用于高維尋優。和理論最優值。參與對比的新型群智能算法有螢火蟲算法(FA)[13]、布谷鳥算法(CS)[14]、人工魚群算法(AFSA)[15]。設置各算法種群規模為40,最大迭代次數為1 000,分別在10維、30維、50維條件下,獨立運行30次取解平均值和方差,結果如表7所示。 表7 CEC2013函數優化結果對比Table 7 Comparison of CEC2013 functions optimization results 分析表7 數據,最優指標數據已經加粗顯示,可以看出,與其他算法相比,無論是低維還是高維,BASTLBO算法均能在CEC2013單峰、多峰以及復合函數上找到更好的結果,進一步證明BASTLBO具有較好的收斂精度和魯棒性。 上述實驗中僅使用了平均值和方差兩種評價指標,為了增強實驗結果的說服力,采用顯著性水平α=5%的Wilcoxon 秩和檢驗[16]方法來進一步評估BASTLBO 算法的性能。如表8所示,其中符號“+”“-”和“=”分別表示BASTLBO算法的結果優于、劣于和相當于對比算法的測試結果。 當p值小于5%時,拒絕零假設,說明兩種算法之間具有顯著性差異。從表8的Wilcoxon統計結果來看,當顯著性水平為5%時,BASTLBO算法與另外三種群智能對比算法之間具有顯著性差異,且BASTLBO明顯更優。 表8 Wilcoxon秩和檢驗結果統計Table 8 Statistics of Wilcoxon test results BASTLBO 算法求解無約束測試函數的有效性和優越性已經得到驗證,為了驗證其對約束問題的求解能力,選擇壓力容器設計優化這一實際結構優化問題來進行實驗,使用BASTLBO求解最小總成本。式(15)給出了該問題的目標函數,約束條件見式(16)。其中x1、x2、x3、x4分別表示實際問題中的半球形封頭厚度Ts、圓柱形壓力容器厚度Th、內徑R和圓柱長度L。 其中,1×0.062 5 ≤x1,x2≤99×0.062 5,10 ≤x3,x4≤200。 為評判求解結果的優劣,將BASTLBO算法與廣泛學習粒子群算法(CLPSO)、協同差分進化算法(CEDE)以及人工免疫混合遺傳算法(GA-AIS)進行比較實驗[17]。為保證公平性,各算法種群規模設置為50,均獨立運行30次,取優化結果均值。對比數據如表9、表10所示。 表9 壓力容器設計問題中約束函數值對比Table 9 Constraint function values comparison in pressure vessel design problem 表10 不同算法在壓力容器設計問題上的優化結果對比Table 10 Optimization results comparison of different algorithms in pressure vessel design problem 綜合表9、表10數據可以看出,BASTLBO算法的優化結果更好一些,其迭代50 000次得到的總成本比其他三種算法要更低。約束函數值也證明了BASTLBO 求解此問題的有效性和優越性,g3函數值達到了0,約束函數g1、g2、g4的值也更接近0,其中g1、g2約束函數值至多提升了9個數量級。 針對TLBO算法易陷入局部最優、求解精度低的弱點,本文提出如下三方面的改進。 (1)在種群初始化階段,結合Tent 映射和反向學習機制,根據適應度值排序,擇優組成初始種群,提高了種群多樣性,且有利于算法快速收斂。 (2)在迭代過程中對教師個體執行BAS搜索,并對BAS進行改進,增強TLBO算法對當前最優個體周圍區域的精細搜索,提高跳出局部最優的能力。 (3)在學生個體更新公式中加入混合變異算子,利用柯西函數較強的局部變異能力和高斯函數較強的全局變異能力,使算法隨迭代進程自適應調節探索方向,既維持了算法的收斂速度,又可以在陷入局部最優時迅速跳出。 實驗結果表明,本文提出的BASTLBO算法在低維和高維下的尋優均具有較好的求解精度和魯棒性,收斂速度快。并通過對壓力容器設計優化問題的求解,驗證了BASTLBO 算法解決約束優化問題的有效性和優越性。未來還會借鑒其他隨機搜索算法的優點,來進一步改善算法性能,同時也將深入研究拓展該算法的應用領域。2.3 學生的混合變異
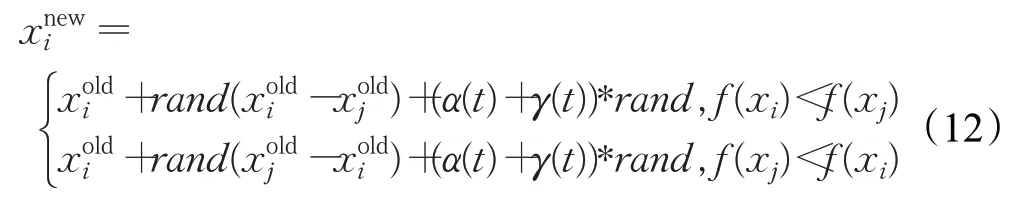
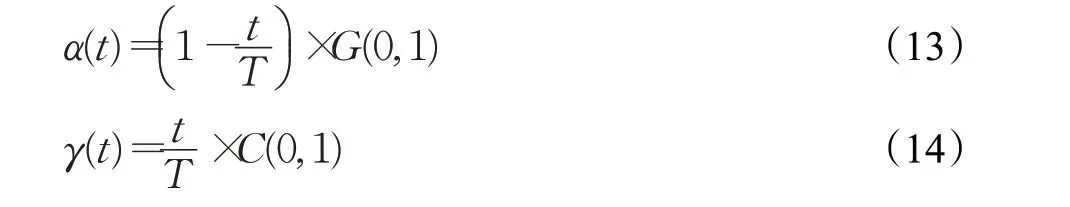
2.4 BASTLBO算法的步驟
3 實驗與分析
3.1 標準測試函數

3.2 天牛須搜索改進有效性分析
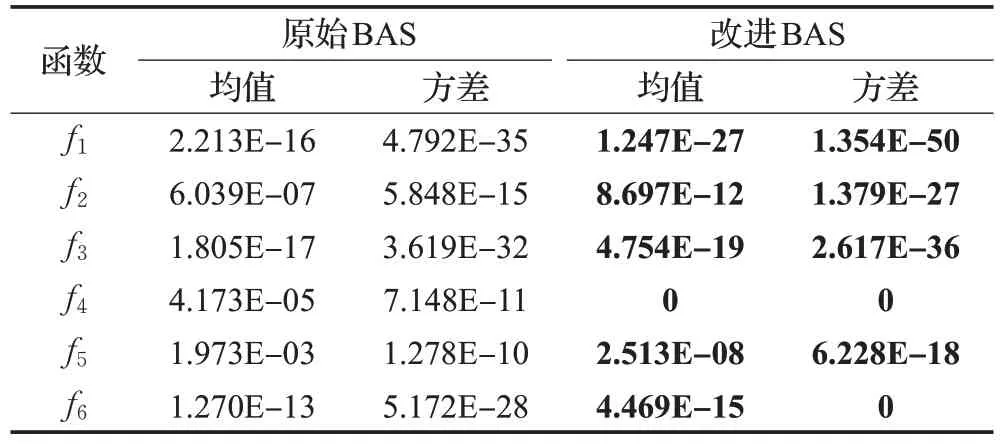
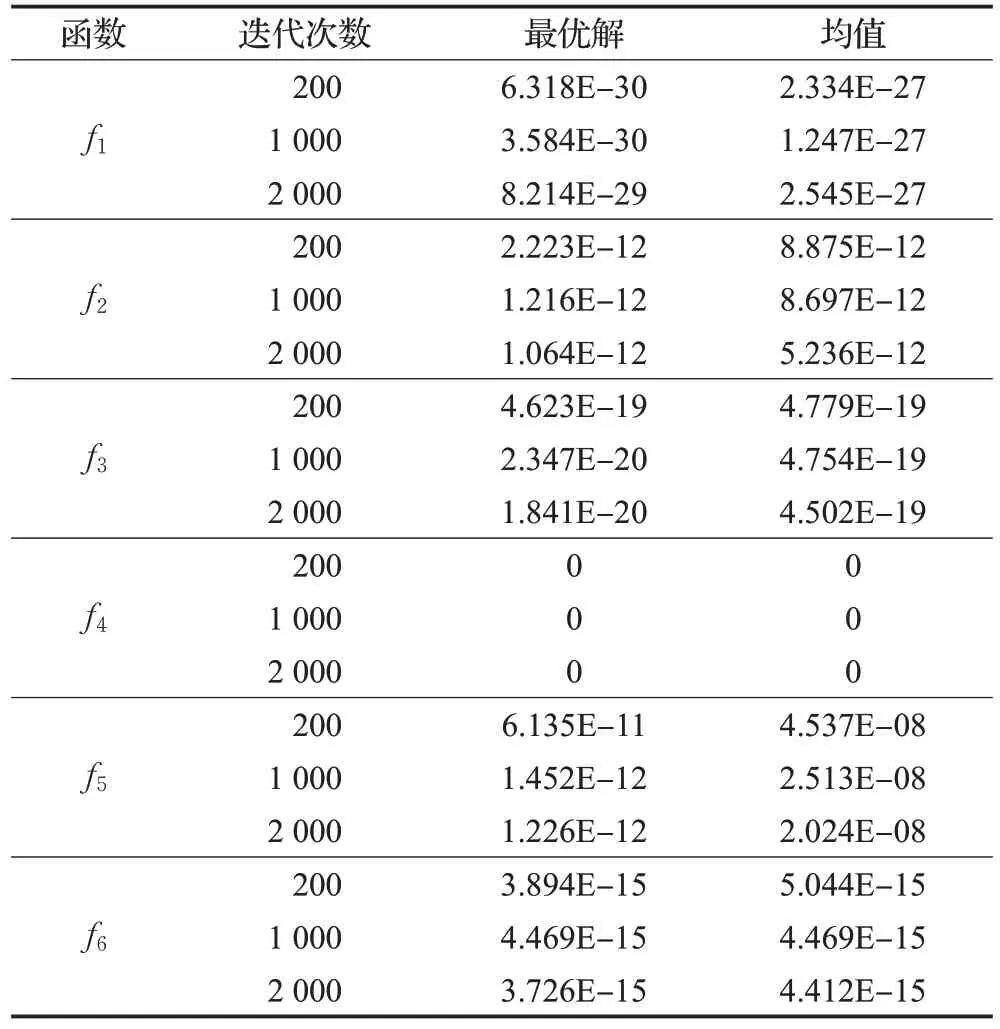
3.3 不同改進策略單一有效性分析
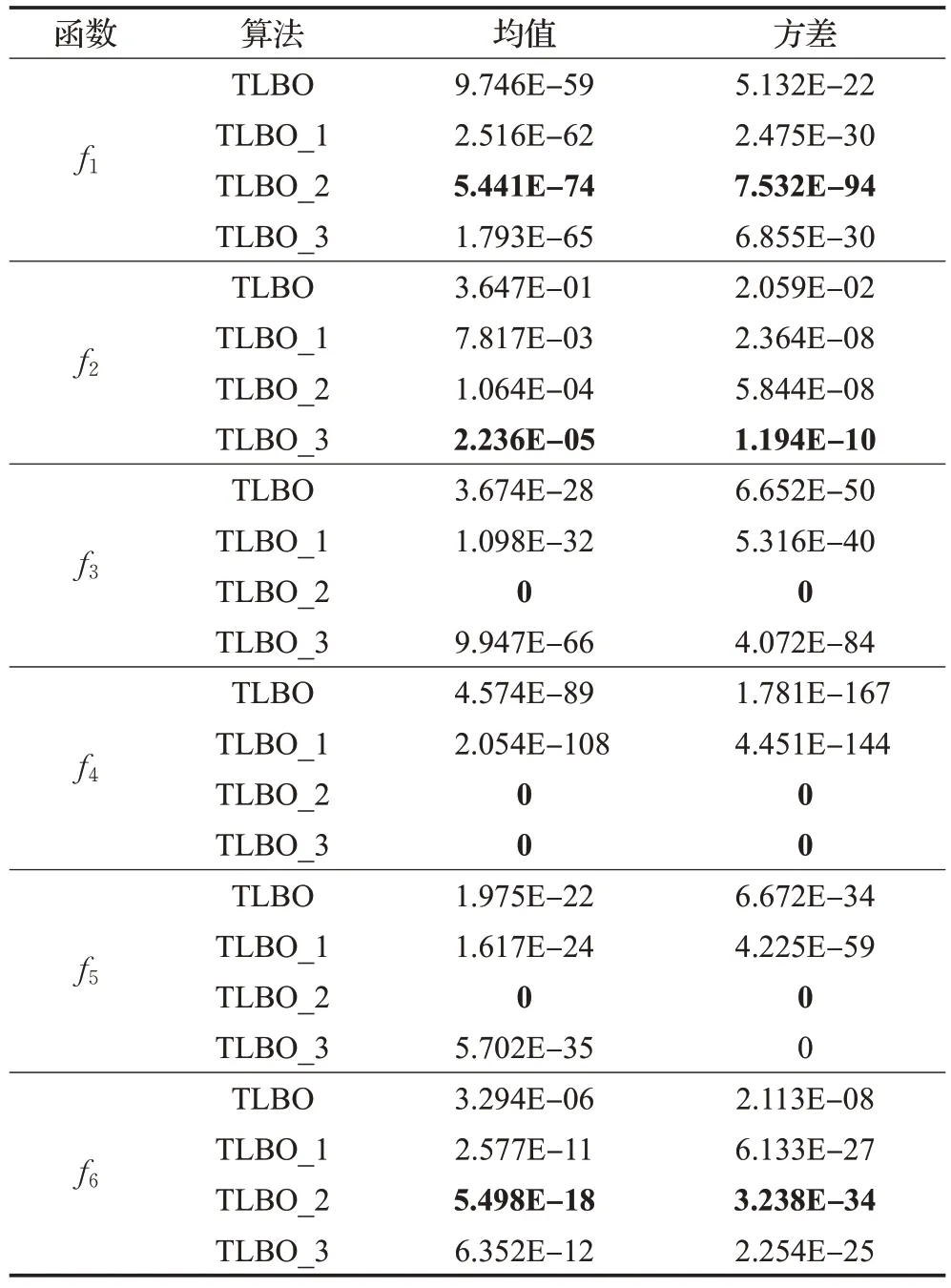
3.4 BASTLBO算法性能測試
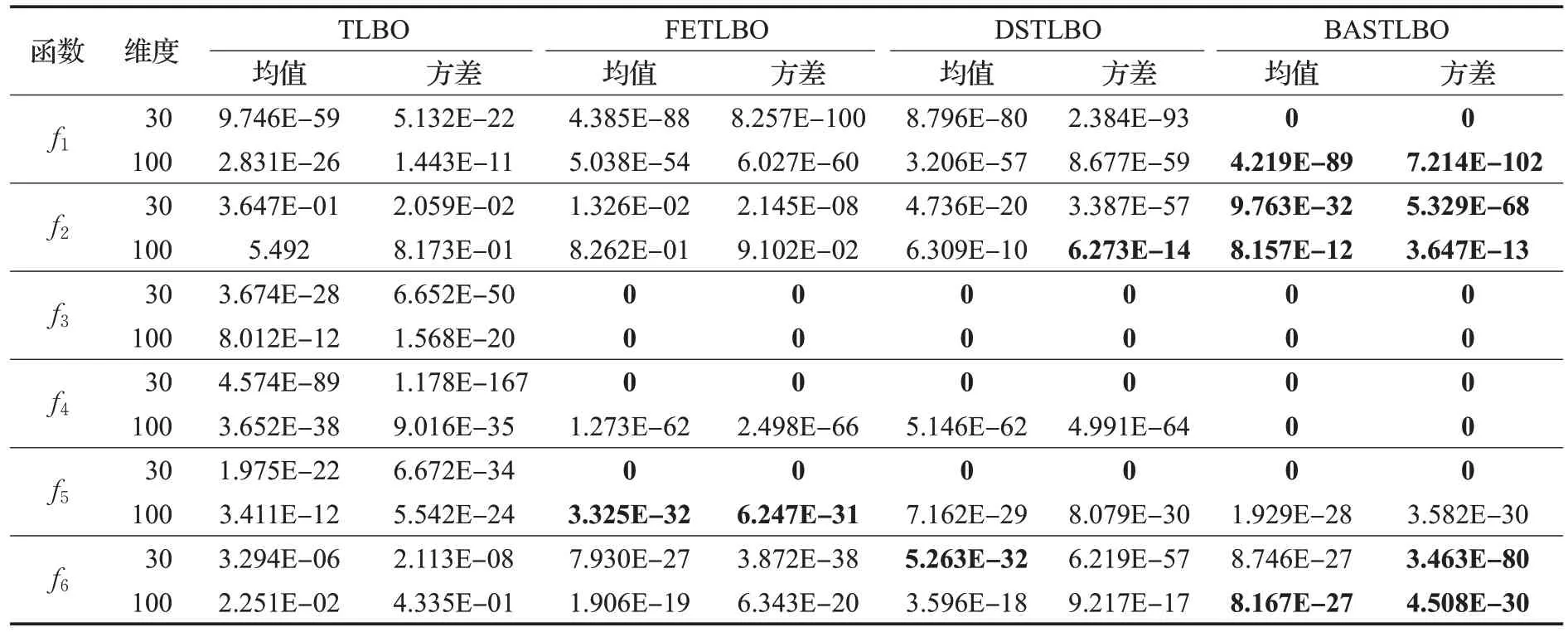
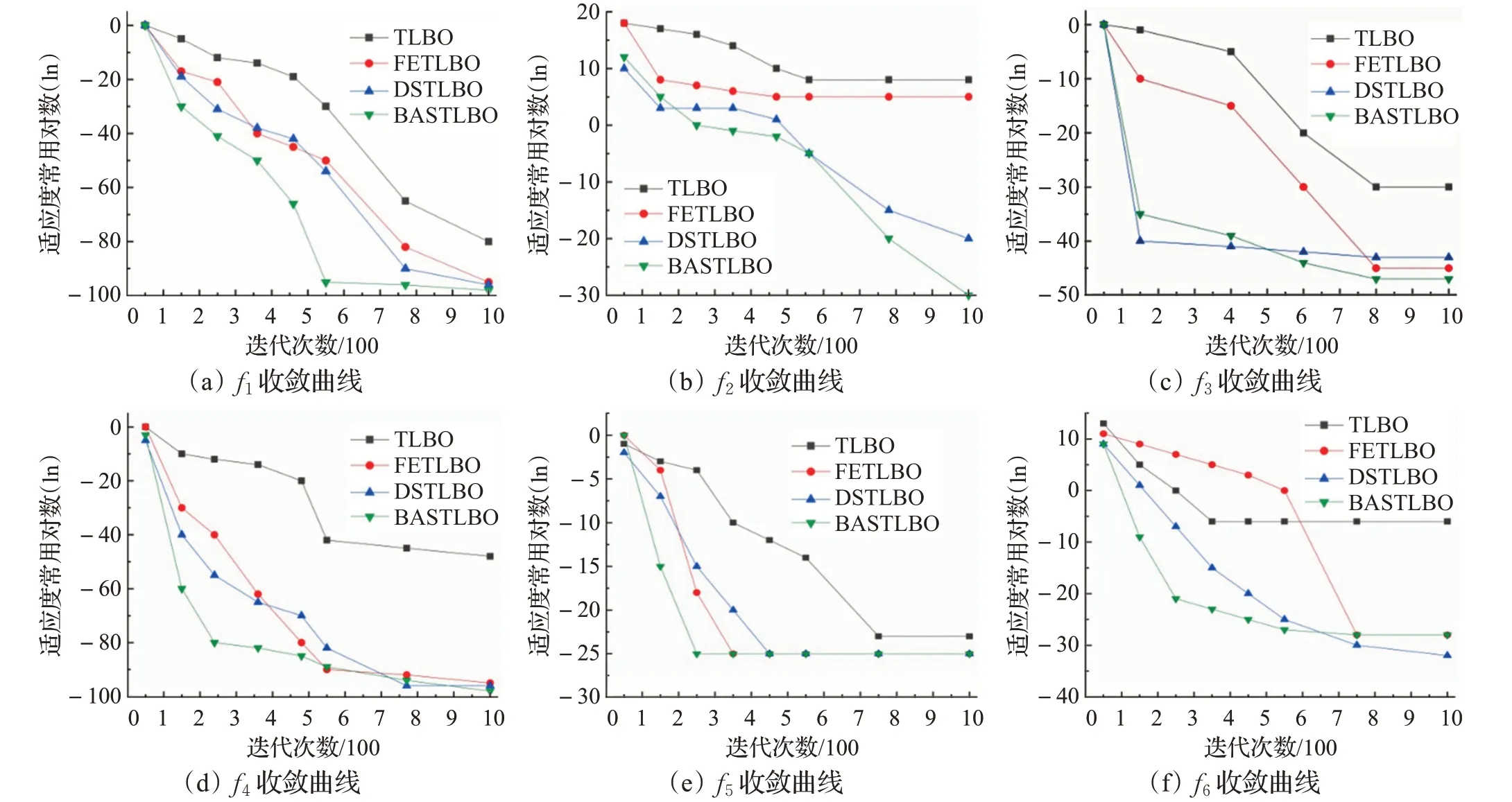
3.5 與其他群智能算法對比
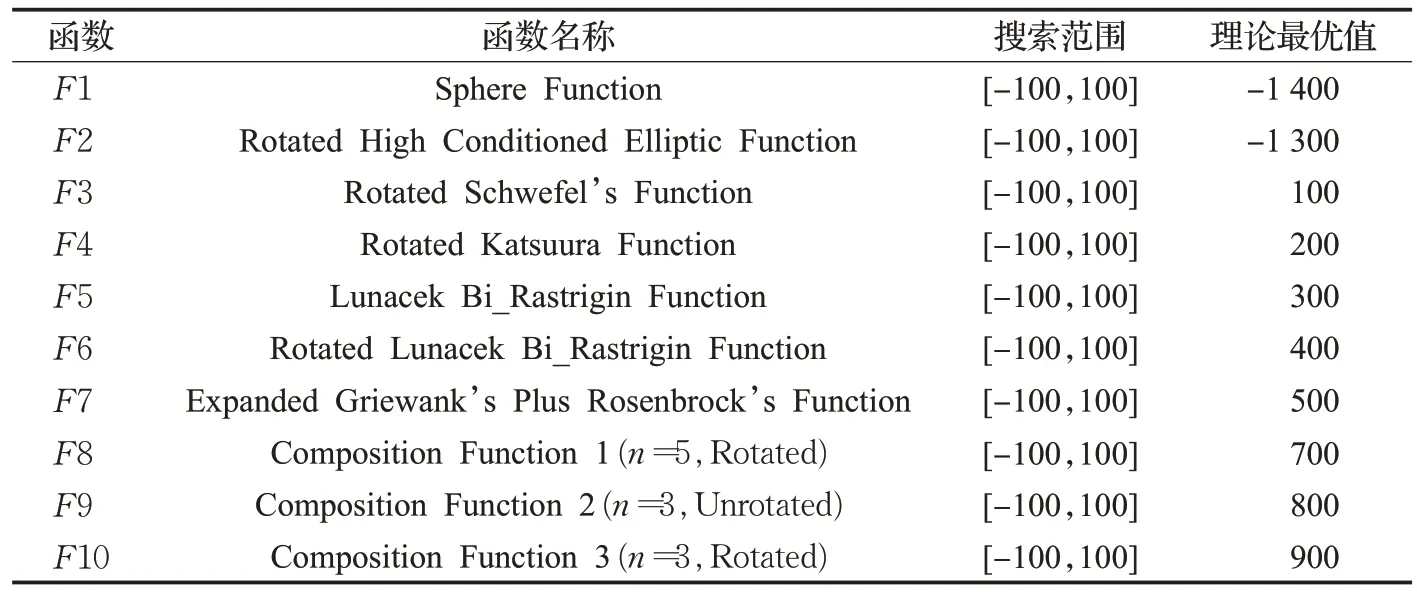
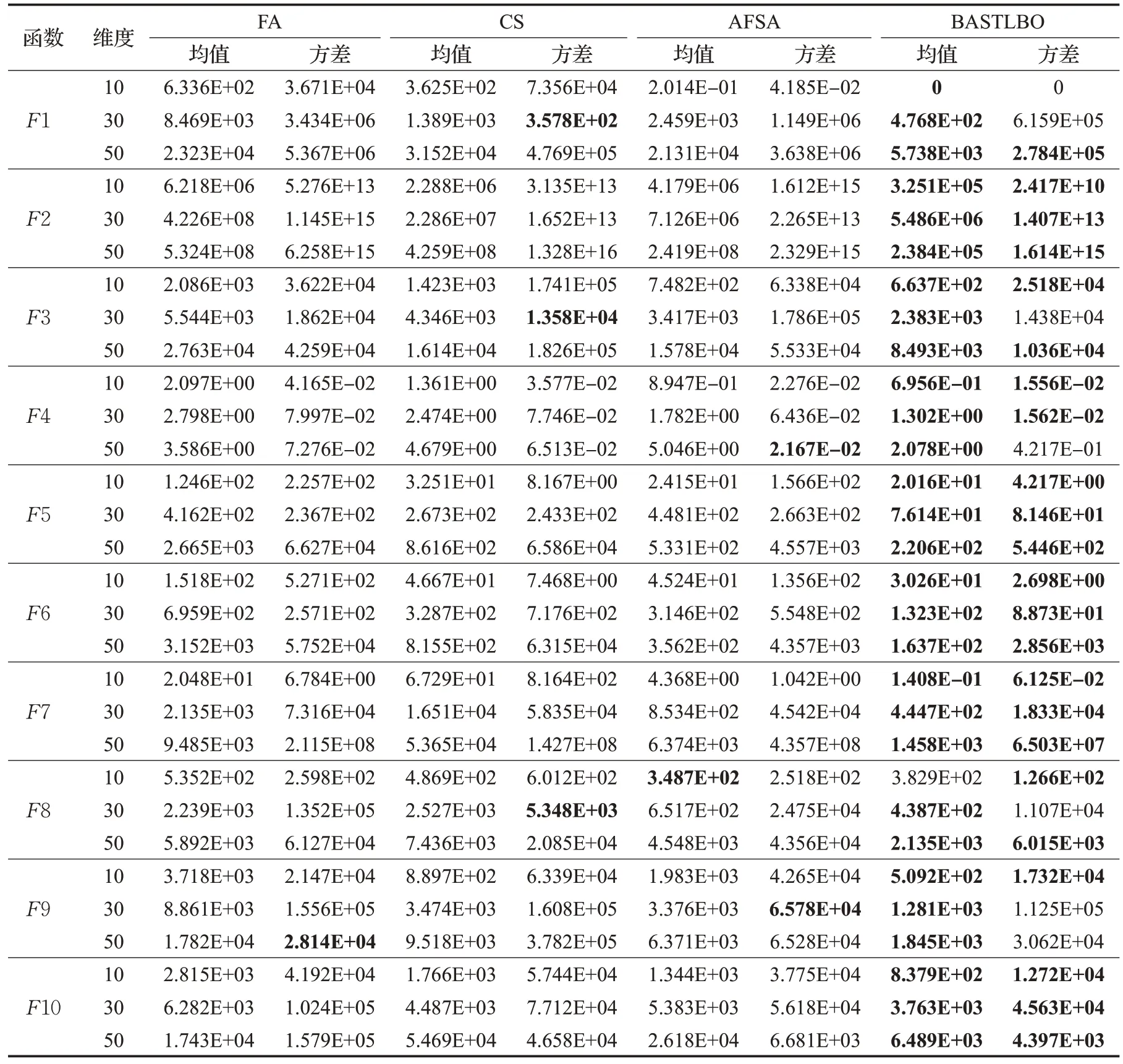
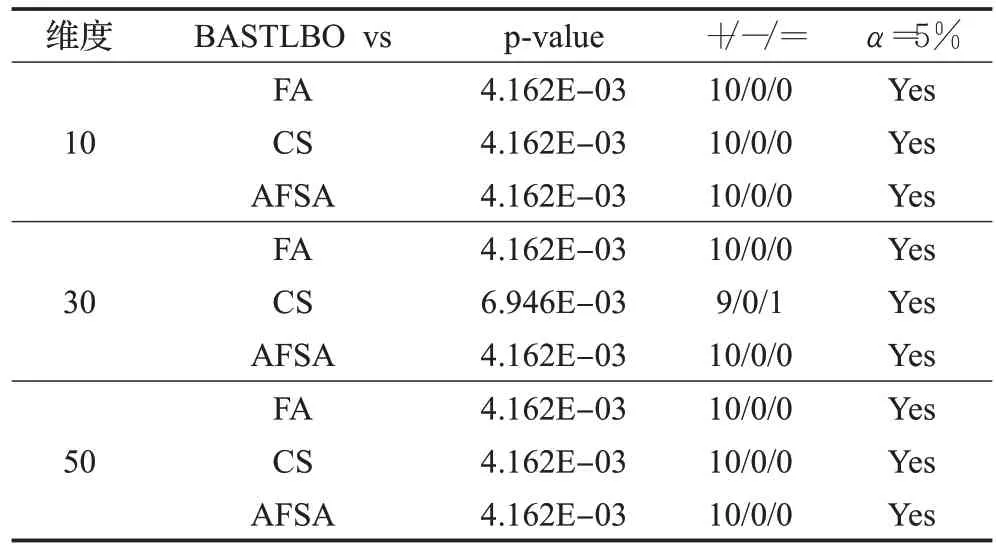
3.6 用壓力容器設計優化問題驗證算法
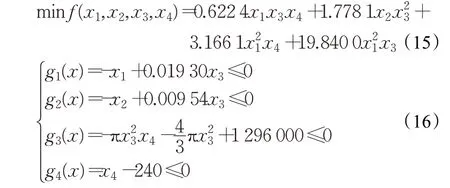


4 結束語

