壓力對實際氣體熱力學能影響的宏觀及微觀分析*
張克舫 王照亮 劉安源 吳明鉑
[中國石油大學(華東)新能源學院 山東 青島 266580]
1 引言
熱力學能(也稱為內能)u和焓h=u+pv是物質重要的狀態參數,也是工程技術中用途廣泛的熱力學函數[1].J.L.Gay-Lussac在1807年,J.P.Joule在1843年,分別做了著名的Joule實驗[2],推導出理想氣體的內能u與焓h都僅為溫度T的單值函數而與壓力p和體積V無關.J.P.Joule和W.Thomson在1852年進行了Joule-Thornson實驗[2],推導出實際氣體的內能與焓都不只是溫度的函數,而是與壓力、體積都有關,即對于實際氣體有u=F1(T,p),h=F2(T,p).
實際氣體的熱力學能和焓值不僅與溫度T有關,還取決于壓力p或比體積v.工程上遇到的實際氣體(例如水蒸氣、油氣田開采的天然氣等),相同壓力下,溫度T越高,熱力學能和焓越大,這很容易理解.那么相同溫度下,壓力越高,實際氣體的熱力學能和焓值如何呢?我們選取工程上常見的水蒸氣和天然氣為例回答這個問題.
水蒸氣是實際工程中廣泛應用的工質,表1是從過熱蒸汽熱力學性質圖表中截取的不同壓力和溫度下水蒸氣的狀態參數.從表1中數據可以看出,在相同溫度下,壓力分別為0.5 MPa,1 MPa,2 MPa時,2 MPa時的熱力學能和焓最小,壓力為0.5 MPa時,熱力學能和焓值最大.

表1 不同溫度、壓力下過熱蒸汽的熱力學能和焓值[3]
REFPROP是一款國際權威工質物性計算軟件[4],圖1是根據REFPROP軟件的數據繪制的水蒸氣焓熵圖,圖中橫坐標是熵,縱坐標是焓,右邊3條實線是干度x為0.9,0.95,1.0的等干度線,兩條虛線是溫度T分別為350 K(77 ℃)和400 K(127 ℃)的等溫線,兩條點劃線是壓力p為 0.15 MPa和0.9 MPa的等壓力線.從圖1可以看出,在相同溫度時(例如T=400 K的等溫線上),p=0.15 MPa的過熱蒸汽比焓大于p=0.9 MPa時過熱蒸汽的比焓值.也就是說,相同溫度下,壓力越高,過熱蒸汽的熱力學能u和焓h越小.

圖1 水蒸氣的焓熵圖
表2是根據REFPROP軟件查到的某組分天然氣的狀態參數,從表2可以看出,天然氣組分一定時,相同溫度下,壓力越高,天然氣的熱力學能u和焓h越小.

表2 組分一定,不同溫度、壓力下天然氣的熱力學能和焓值
表1、表2和圖1的數據都表明了,相同溫度T下,壓力越高,水蒸氣和天然氣的熱力學能和焓值越小,這與我們一般的感性認識背道而馳,怎么解釋此現象呢?其他的實際氣體是否也具有相似的規律呢?在《大學物理》及《工程熱力學》等教材中,都沒有給出答案以及解釋,學習者特別是工程技術人員很容易產生困惑, 本文從宏觀的實際氣體狀態方程及熱力學能統計定義微觀的角度出發,推導分析壓力對實際氣體的熱力學能的影響,從理論上證明了在相同的溫度下,壓力越高,比熱力學能和焓值越小.
2 從實際氣體狀態方程角度分析
對于實際氣體,人們已經提出了上百個半經驗與純經驗狀態方程,盡管方程的復雜性和精度不同,但都考慮了氣體分子自身大小和分子之間的相互作用力,是對實際氣體pVT行為的一種近似描述.其中范德瓦耳斯方程是最經典的方程之一, 即
(1)
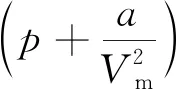
熱力學能的全微分表達式為
(2)

2.1 單獨考慮分子體積修正項時
當單獨考慮分子體積修正項時有
p(Vm-b)=RT
(3)
從式(3)可以求得
代入到式(1)可得
(4)
(5)
由式(5)可見,分子體積修正項對du沒有影響.
2.2 單獨考慮分子引力時
單獨考慮分子引力時有
(6)
從式(6)可以求得
代入到式(2)可得
(7)
(8)
由式(8)此可見,隨著體積的增大,熱力學能是增大的.而體積與壓力成反比,因而壓力增大時,體積減小,熱力學能減小.
2.3 同時考慮分子體積修正及分子引力時
范德瓦耳斯方程在理想氣體狀態方程的基礎上,對分子體積項以及分子間的引力項進行了修正.由以上分析可知,在定溫條件下,分子體積修正項對熱力學能的變化沒有影響,也就是壓力變化(或比體積的變化)時,熱力學能不變化;但對于分子間的引力一項,隨著壓力的增大(比體積減小),熱力學能是減小的.因此兩者的綜合作用就是,隨著壓力的增大(比體積減小),熱力學能是減小的.
3 從熱力學能的統計定義角度分析
從統計角度看,單原子經典氣體的熱力學能U等于分子動能與分子勢能之和,當氣體的密度不是很高時
(9)
其中,pi是第i個分子的動量,即第一項是體系中分子的動能;ri,j是兩個分子之間的距離,φ(ri,j)是兩分子相互作用勢能[9],反映兩個分子間相互吸引作用的強弱.
由式(9)中第一項可以看出,分子的動能與其質量和速度有關,溫度一定時,體系中分子的動能是確定的,不隨分子間距或壓力而變化.但是考慮分子間的引力,即表現為式(9)的第二項,式(10)的Lennard-Jones勢是常用分子勢能曲線的表示分子作用勢的半經驗公式[9]
(10)
式中,r0和φ0是相互作用勢能的兩個參量.當兩個分子相距r0(10-10m的數量級)時,相互作用勢能達到極小值-φ0.
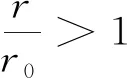
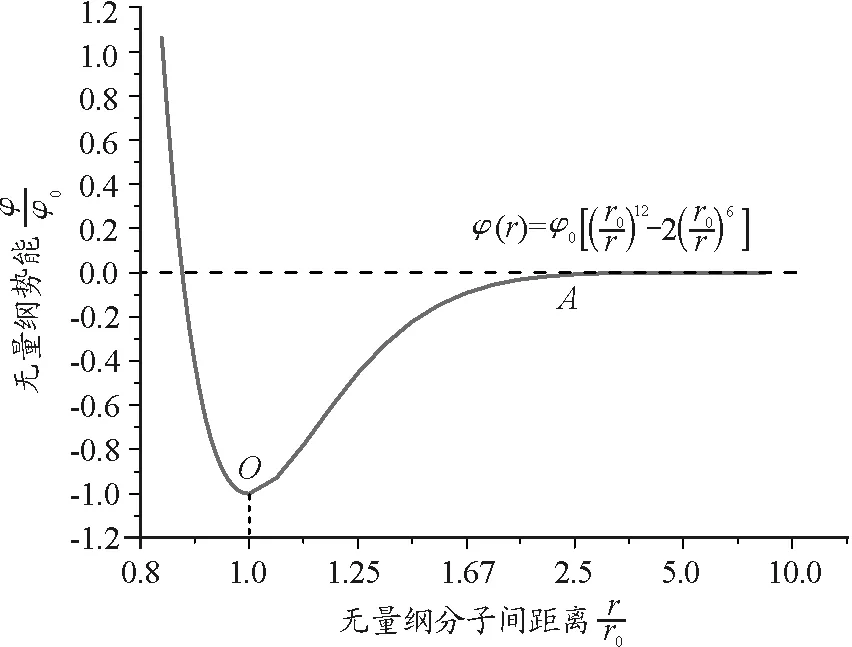
圖2 Lennard-Jones分子勢能曲線
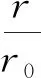
氣體壓力p增大時,熱力學能減小,也可以從能量角度定性分析.由于實際氣體的分子間總存在著相互作用(吸引力),當壓力減小或體積增大時,必須吸收能量以克服分子間的吸引力,所以吸收的能量導致熱力學能增加.
4 結論
(1)對水蒸氣和天然氣這樣的實際氣體來說,溫度相同時,壓力越高,比熱力學能和焓值越小.
(2)根據宏觀的范德瓦耳斯實際氣體狀態方程,在定溫條件下,分子體積修正項對熱力學能的變化沒有影響;但對于分子間的引力一項,隨著壓力的增大(比體積減小),熱力學能是減小的.兩者的綜合作用是,隨著壓力的增大(比體積減小),熱力學能是減小的.
(3)根據微觀的熱力學能統計定義,溫度一定時,體系中分子的動能不隨分子間距或壓力而變化;根據Lennard-Jones勢能曲線和公式,當r>r0時,隨著氣體分子間距r的增大,分子作用勢φ是增大的.
(4)宏觀的范德瓦耳斯實際氣體狀態方程及微觀的熱力學能統計定義,都證明了相同溫度下,實際氣體的熱力學能U隨著壓力的增大而降低.

