范德瓦耳斯氣體體積修正的新計算方法*
藍善權
(嶺南師范學院物理科學與技術學院 廣東 湛江 524048)
1 引言
1 mol理想氣體物態方程為
pVm=RT
(1)
理想氣體模型中的氣體分子是質點,沒有體積.而實際氣體分子是有體積的,特別是當氣體很稠密時,體積對物態方程的修正是很明顯的,它的效果相當于分子間的排斥力.再考慮到分子間的吸引力作用,實際氣體物態方程可以更好地近似為范德瓦耳斯方程[1,2]
(2)
式中參數b表征的就是因分子體積而帶來的修正值,它由實驗測定.此外,也可以從理論上證明參數b的數值約等于1 mol氣體所有分子體積總和的4倍[3~5].本文介紹一種新的計算方法求參數b.
2 體積修正的新計算方法
如圖1所示,設有兩半徑為r的全同小球1和小球2相互碰撞,其中小球2固定不動,小球1可以從各個方向撞向小球2,則小球1的質心不可到達的區域如圖2虛線所示,該區域的體積是

圖1 兩小球相互碰撞示意圖

圖2 碰撞過程中小球的有效體積示意圖
(3)
設想有1 mol氣體在體積為Vm的容器中,現在要計算這NA個氣體分子的有效活動空間Vm-b,即計算參數b的值.首先,對NA個氣體分子進行編號,令第1個分子為質點,其他分子都“凍結”在一定的位置上,在分子1和其他分子碰撞的過程中,其他分子小球的有效半徑為d,如圖2虛線所示.則對于第1個分子,它的不可活動空間是(NA-1)V0.然后,令第1,2個分子為質點,在分子2和其他分子碰撞的過程中,其他有效半徑為d的分子球都處于“凍結”狀態.則對于第2個分子,它的不可活動空間是(NA-2)V0.接著,令第1,2,3個分子為質點,在分子3和其他分子碰撞的過程中,其他有效半徑為d的分子球都處于“凍結”狀態.則對于第3個分子,它的不可活動空間是(NA-3)V0.以此類推,可得對于第NA個分子,它的不可活動空間
(NA-NA)V0=0
對所有NA個分子來說,總的不可活動空間是
V=[(NA-1)+(NA-2)+(NA-3)+
(4)
因此,對任意一個分子,平均的不可活動空間(即參數b的值)為
(5)
為什么在計算第2個分子的不可活動空間時,要把第1個分子當成質點?因為第1,2個分子之間的相互碰撞,已經在計算第1個分子的不可活動空間時考慮了,不能重復計算碰撞事件,以此類推,在計算后面分子的不可活動空間時,需要把前面的分子當成質點.
3 總結和討論
采用新方法,通過考察每一對分子的相互碰撞,計算得到了因分子體積不能忽略而給系統帶來的有效體積的修正,結果與其他方法得到的結果一致.下面簡要介紹參考文獻中的計算方法,并與本文的新方法進行比較.
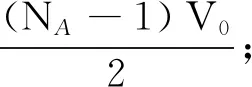

參考文獻[4]中參數b的數值為

參考文獻[5]介紹了由臨界點的參數來表示參數b,對氦氣的參數b給出了5種表達式和相應的數值,有些數值與4倍所有分子體積總和近似,而有一個數值偏差較大.

