基于無監督學習的岸邊集裝箱起重機關鍵部件故障診斷方法*

張 氫 李帥杭 陳 星 肖炳林 李 恒

1同濟大學機械與能源工程學院 上海 201804 2海南省鍋爐壓力容器與特種設備檢驗所 海口 570203

3廣州港股份有限公司南沙集裝箱碼頭分公司 廣州 510100

0 引言

海洋運輸是最主要的國際物流運輸方式，它承擔了我國進出口貨運總量的90%。岸邊集裝箱起重機（以下簡稱岸橋）是整個碼頭完成貨物從海洋到陸地轉移的核心裝備。為防止岸橋發生故障導致的碼頭效率降低、停工，甚至人員安全事故，針對岸橋的故障檢測是十分必要的。如今，我國的集裝箱碼頭正在陸續進行智能化改造，同時建設新的自動化、智能化碼頭。

目前，對齒輪箱的故障診斷研究正在飛速發展，針對齒輪箱振動數據的診斷方法較多[1-3]。然而這些方法大耗費時間較長，需要額外設計診斷模型的自我更新等問題。在對齒輪箱的無監督故障診斷領域中，現有的研究并不多。Luo J等[4]提出了一種基于流形學習和支持向量機的半監督學習方法，通過少量的標記樣本訓練，從行星齒輪箱試驗臺中獲取數據，實驗驗證了其方法的有效性。Cheng G等[5]將從EMD分解后獲得的能量特征值作為無監督的SOM網絡的數據輸入，進行故障分類，實驗證明該方法能夠準確地提取和區分這些信號的故障特征。李狀[6]利用C均值聚類算法對ART2神經網絡的分類性能進行了優化，在風電機組齒輪箱的實機信號上成功進行了無監督的故障診斷。這些方法能夠在試驗臺數據或運行較為穩定的風機齒輪箱中獲得較好的診斷結果，但岸橋齒輪箱的工況更加復雜、存在大量的加速減速和正反轉運動，使得其故障診斷尤其是無監督的故障診斷難度增大。在基于岸橋齒輪箱的大數據故障檢測中，遇到的很大的問題是故障數據缺失，無法訓練，也無法自行學習更新。

本文提出了一種基于無監督機器學習的岸橋齒輪箱故障檢測方法。通過對岸橋的振動信號進行處理，提取能夠反應其狀態的特征值，然后通過無監督的機器學習方法判斷齒輪箱的健康狀態。

1 振動信號的特征值

在對信號進行聚類分析前，首先要明確聚類的對象，性能良好的對象應該能夠表征當前信號的數據模式，這些數據模式不應受到轉速、載荷等其他因素的影響，能夠正確區分正常模式的數據與故障模式的數據。此外，為了減少無監督聚類的訓練時間，聚類對象需要盡可能的正交，即去除冗余的特征值，保留下能夠充分表征當前信號的特征值。

1.1 特征值提取

實際中采集到的振動信號為一段隨機的離散信號，為了反映該段信號的振動模式，以該段信號的統計特征值作為表征該信號的特征值。振動信號的統計特征值可分為兩類，時域統計特征值與頻域統計特征值。

本文采用的時域統計特征值包括均值、標準差、均方根值(有效值)、峰值指標、脈沖指標、波形指標、峭度指標、偏度指標、裕度指標等。其中標準差反映了信號圍繞均值的波動程度，描述了信號的波動分量；均方根值描述了振動信號的能量，穩定性好，重復性好；峰值指標和脈沖指標可用來檢測信號中是否存在沖擊；峭度指標對信號的沖擊特征很敏感，當數值過大時，表明機械中可能存在由于間隙過大、滑動副表面存在破損等原因導致的沖擊性振動；裕度指標可用于檢測機械設備的磨損情況；偏度指標反映振動信號的非對稱性。

頻域統計特征包括功率譜重心指標、均方譜、功率譜方差、相關因子、諧波因子、譜原點矩等。功率譜是反映單位頻帶內信號功率隨頻率的變化情況，也就是信號功率在頻域內的分布情況。功率被定義成幅值的平方的時間平均分量，而這個過程也可以看做是去除頻域諧波分量的相位信息的過程。功率譜重心指標反映了能量重心位置的變化程度，可以較好地描述信號頻域特征的變化；功率譜方差反映了能量分布的離散程度；功率譜均方頻率表征功率譜主頻帶的位置；相關因子反映了譜能量分布的相關程度；諧波因子反映了譜的分布狀態和譜寬情況；譜原點矩反映功率譜的總體能量情況。

這些時域、頻域特征值能夠較好地反映機械設備在故障狀態與非故障狀態下的差異[7,8]，選擇其構成的特征矩陣作為機器學習的對象。

1.2 特征值歸一化

不同的特征值之間存在較大的數量級差異，需通過各特征值歸一化來避免某一較大的特征值占據主導地位。

Z-Score標準化既適用于數值比較集中的情況也適用于數值分散的情況，且能保證歸一化結果相對穩定。此外，Z-Score標準化在分類、聚類算法中或者使用PCA等技術進行降維時，其性能表現較好，故本文選用Z-Score標準化。

Z-Score標準化后數據符合標準正態分布，即均值為0，標準差為1，其轉化函數為

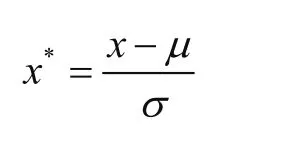
式中：μ為所有樣本數據的均值，σ為所有樣本數據的標準差。

1.3 特征值降維

因為各特征值之間可能存在信息重疊，為了提升機器學習的效率，減少不必要的計算量，在提取了上述信號特征之后需要對特征值進行降維，本文采用主成分分析法（PCA）對特征進行降維，利用正交變換來對一系列可能相關的變量的觀測值進行線性變換，從而投影為一系列線性不相關變量的值，這些不相關變量稱為主成分。

求解歸一化后的特征值矩陣的協方差矩陣，再求出其協方差矩陣的特征值，就可以得到各個成分的貢獻率。貢獻率表明主成分綜合變量數據的能力，貢獻率越大說明其綜合原始變量數據的能力越強。一般選取排名靠前且累計貢獻率大于80%的主成分。

2 無監督聚類

在有監督機器學習方法中，需要獲取大量的有標簽數據作為輸入，具體到故障檢測領域中，即需要大量的實際故障數據作為訓練集與測試集。然而，目前在港口機械中，由于機型眾多，機構組成復雜，工況各異，這些小樣本的監督學習標簽局限性比較大，同時這些標簽數據由于歷史原因又少，在效果上差強人意。

本文考慮使用無監督的方法進行岸橋的故障檢測，目前常用的無監督方法主要有：K-Means、ART2網絡、SOM網絡等聚類方法。K-Means聚類作為一種啟發式算法，極適用于大數據處理任務，目前已經在計算機視覺、天文學、故障診斷等領域取得成功應用。

2.1 K-Means聚類

K-Means算法源于信號處理中的一種向量量化方法，其聚類的目的是：把n個點劃分到k個類別中，使得每個點都屬于離他最近的均值對應的類別[9]。K-Means聚類的步驟為：

1）選取k個聚類中心，也稱其為該類的質心。若完全隨機選取質心，則可能使聚類過程計算量過大，增加不必要的迭代步驟。因此，在選擇質心時需要增大距已選質心較遠的點的被選中的概率。

2）對每個樣本點i，計算其所屬的類別

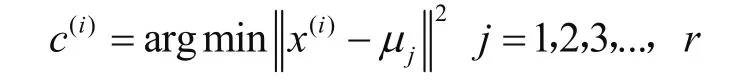
式中：x(i)為樣本，μj為類的質心，c(i)為計算出的樣本所屬的新類，‖a－b‖2為計算兩者間的歐幾里得距離。

此步可具體分為計算距離與尋找新類2步，主要的計算量發生在距離計算中。為加快迭代聚類過程，通過elkan K-means算法，利用三角形的幾何特性可減少大量的計算步驟。

3）對每個類別，重新計算其質心位置

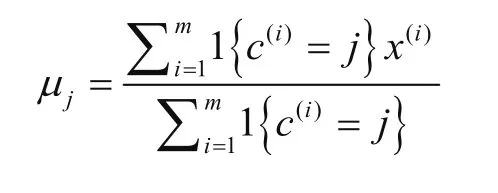
重復2）、3），直至收斂或達到終止條件。

損失函數為

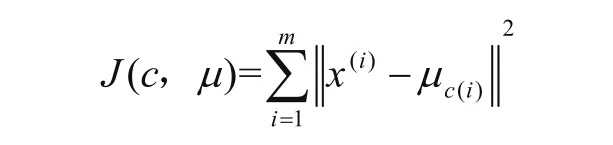
2.2 無監督機器學習流程

本文基于聚類的無監督故障診斷方法由3部分構成：對振動信號進行預處理得到特征矩陣；然后通過PCA算法對特征進行降維；最后通過K-Means算法對簡化后的特征矩陣進行聚類。無監督故障診斷模型如圖1所示。

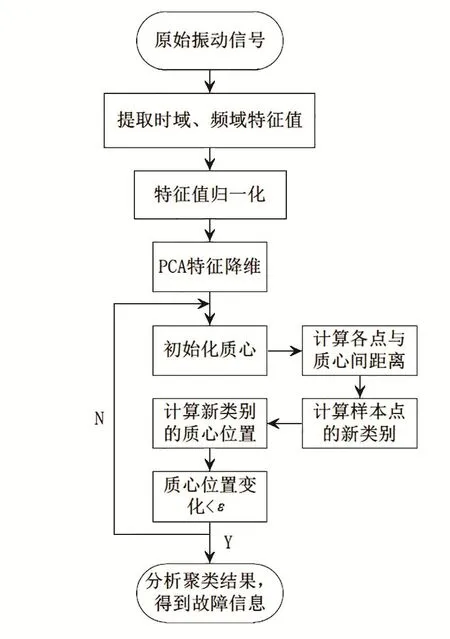
圖1 無監督故障診斷模型

3 實際實驗

3.1 實驗1

采用某大學的公開數據集對本文提出的方法進行驗證。該實驗選擇了安裝有14 in的軸承在采樣頻率12 kHz下的驅動端數據，軸承存在內圈故障、滾動體故障、6點鐘方向的外圈故障，轉速為1 797 r/min。

從3組故障數據中各選出10條故障樣本，再加上從3組對應的正常數據中各選出30條樣本，組成總數90的數據集。

每條數據可計算出20維特征值，對特征值矩陣歸一化后進行PCA主成分分析。為了便于可視化分析與展示，設置約簡后的特征維數為3，可以計算出最終的3維特征值主成分貢獻率之和為88.83%，認為能夠表征原特征空間。

表1所示為某大學數據集中部分樣本特征值示例，0～5為正常樣本特征值，70～72為滾動體故障樣本特征值，87～89為外圈故障樣本特征值。對比表中各特征值可知，經過上述處理流程后，不同故障類型的樣本能夠明顯區分開。

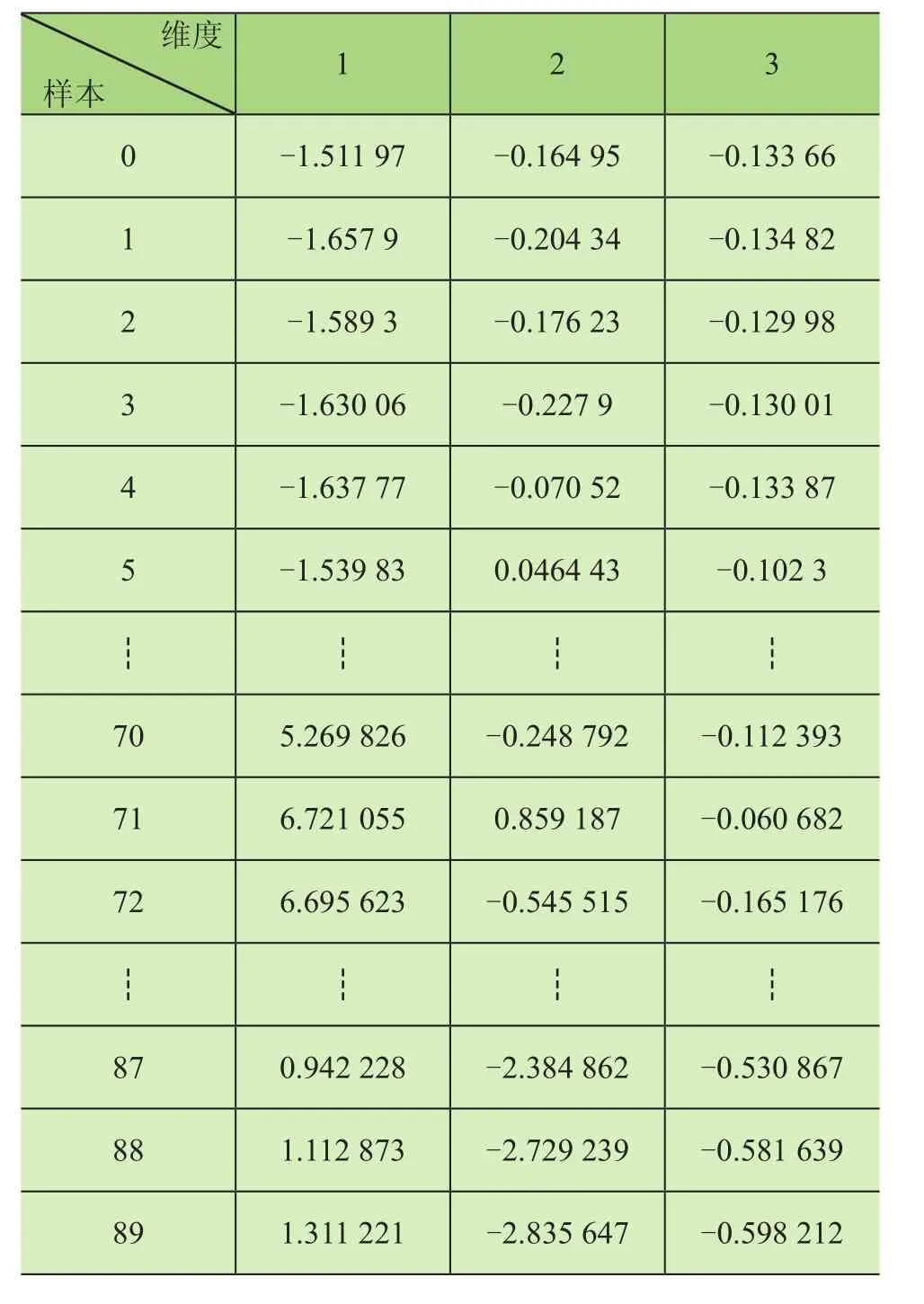
表1 各樣本特征值

在對經過PCA后的特征矩陣進行聚類分析，設置聚類類別為4。通過K-Means算法將這90條數據分為4類，每類樣本數分別為60、17、12、1。選取前2維特征值對聚類結果進行可視化，如圖2所示。

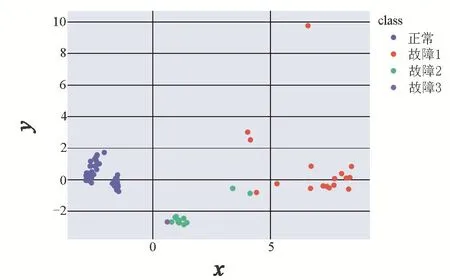
圖2 某大學數據集聚類結果

3.2 實驗2

采用國內某碼頭岸橋設備的實機振動信號作為數據源。如圖3所示，為岸橋起升機構的傳感器安裝示意圖，共7個測點。

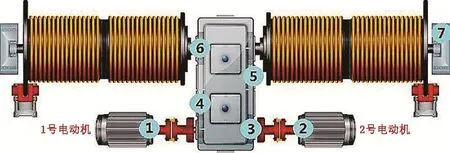
圖3 傳感器布置

起升機構上7個傳感器的采樣頻率為51 200 Hz與25 600 Hz。電動機轉速800～1 200 r/min，岸橋裝卸集裝箱質量范圍為28～65 t。

當該岸橋出現異常時，將該時刻的數據添加到總數據集中，即可運用本文提出的無監督方法分辨出該異常數據。此次實驗的數據集中包含示例岸橋的某一個時刻檢測到的異常實際數據，后經停機拆箱檢查后確認此為一軸承發生故障所致。

起重機原始數據中，各個測點間數據獨立，文以單個岸橋的機構為分析對象，首先對原始數據進行整理，將機構的多測點數據整合為一條。

之后對振動數據進行特征值提取，得到特征矩陣。通過數據歸一化消除特征值間的數量級差異，同時使得后續特征約簡與聚類分析過程的性能得以提升。

將歸一化后的特征值矩陣通過PCA進行降維，確定最終的特征維數為5。此時，各主成分貢獻率之和為88.06%，表明約簡后的特征仍能夠較為全面的表征原始信號。

通過K-Means方法進行聚類分析，設置最終聚類類別為3，得到聚類結果后發現添加的故障數據被單獨分為一類。選取前2維特征值對聚類結果進行可視化，如圖4所示。實驗證明本文提出的方法能夠分辨出異常的岸橋振動數據。

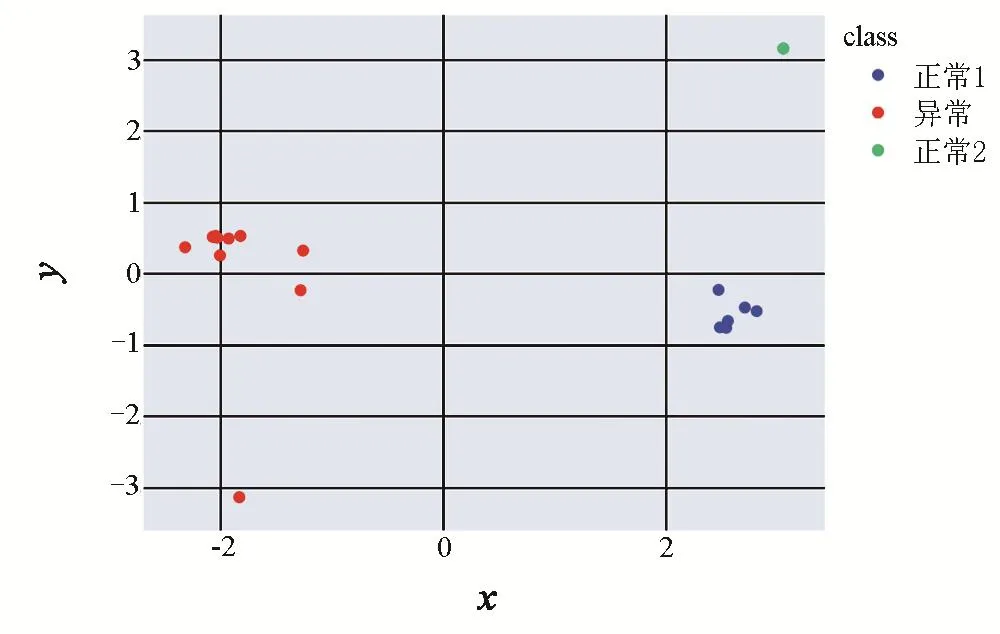
圖4 岸橋實際振動數據聚類結果

4 結論

本文以港口中實際運行的岸橋為對象，進行了故障檢測的研究。針對目前港機缺乏充足的故障標簽數據的情況，提出了一種基于無監督方法的岸橋故障檢測方法。通過提取反映設備當前狀況的特征值，對其進行必要的歸一化與降維，優化數據集，增強了下一步聚類分析的性能。通過實機檢測到的數據進行驗證，實驗結果驗證了該方法的有效性。