快速路上交通事件所致延遲的實時預測*

李翠，張春雨

(江西交通職業技術學院 信息工程系，江西 南昌 330013)

為保證快速路的正常通行能力，路上發生的各種交通事件(如車輛刮蹭、貨物灑落、車輛拋錨等)應得到及時處理。除交通事件的及時偵測外，交通延遲的實時預測也是交通管理部門的重要需求。交通延遲的預測方法大致分為波動法和隊列法。波動法引入沖擊波、擾動清除時間和最大隊列長度等構造由交通事件引起的交通流時空變化模型，其理論模型較精細，需要大量數據支撐。隊列法通過計算到達曲線和離開曲線圍合的面積得到總的交通延遲，意義明確、計算簡單。隊列法又可分為確定性隊列法和隨機性隊列法，前者參數(如到達曲線、交通事件持續時間、離開曲線等)均為已知常數，而后者將各種參數視作隨機變量。確定性隊列法只給出確定的交通延遲預測結果，預測精度往往較差，且只能用于事后評估分析。隨機性隊列法能給出具有一定保證率的交通延遲預測結果，可用于實時預測，但計算較復雜。因此，有必要開發可兼顧預測實時性和計算簡便性的交通延遲預測新方法。為實時預測快速路上由交通事件引起的交通延遲，該文提出改進隊列法，并通過算例分析驗證其有效性和實用性。

1 隊列法的基本原理

如圖1所示，S1表示交通事件被清除后的通行能力，S2表示輸入事件地點的平均速率，S3表示事件持續時間內道路的通行能力，T1表示交通事件從發生到被清除(或稱結束)所持續的時間，T2表示交通事件從發生到道路通行恢復正常所經歷的時間，dmax表示個體車輛的最大延遲。S2對應到達曲線，表示交通需求；S1和S3對應離開曲線，表示通行能力(或服務能力)。

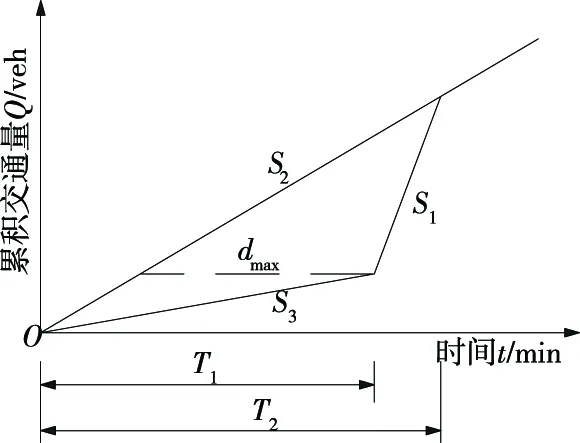
圖1 隊列法計算交通延遲示意圖

到達曲線、離開曲線和事件持續時間均為已知常量，到達曲線和離開曲線圍合的面積即為交通總延遲，其數學表達式為：

(1)

對于在時刻t流入事件地點的個體車輛，其時間延遲為：

(2)

式中：T2按式(3)計算。

(3)

根據圖1，當個體車輛在時刻t=S3T1/S2到達事件地點時，其離開事件地點的延遲最大，為：

(4)

式(1)～(4)描述的是確定性隊列法。該方法計算簡單，但要求各參數均為已知，故只適用于交通事件被清除后的評估分析。如果對以往積累的交通事件數據進行統計分析，可考慮事件持續時間的隨機變化對交通延遲的影響，也可進一步考慮到達曲線和離開曲線的隨機變化，從而構成完整的隨機性隊列法。隨機性隊列法引入概率思想對交通延遲進行分析，計算較復雜。

2 改進隊列法

為實時預測快速路上交通事件所致延遲，對傳統隊列法進行改進。基本思路為：1)基于上游監測斷面采集的交通量信息，利用K近鄰法對到達曲線進行預測；2)利用線性回歸方法估計交通事件的持續時間；3)將下游監測斷面采集的交通量信息和路段的最大通行能力相結合對離開曲線進行擬合；4)參照確定性隊列法預測交通延遲。

圖2為改進隊列法計算交通延遲示意圖。與圖1相比，到達曲線不再為直線，而是呈波浪上升的曲線。到達曲線可根據上游監測斷面采集的交通量信息，利用K近鄰法(或其他預測方法)進行預測得到。離開曲線依然為2段折線，第1段折線根據下游監測斷面短時采集的交通量信息進行平均處理后得到，第2段折線為路段的正常通行能力。在利用線性回歸方法預測事件持續時間的基礎上，將2段折線相連便得到擬合的離開曲線。S2仍然對應到達曲線，但為不斷變化的速率；S1和S3對應離開曲線，均為平均速率。此外，到達曲線并非直線，而是由離散的多個采樣點相連而成。

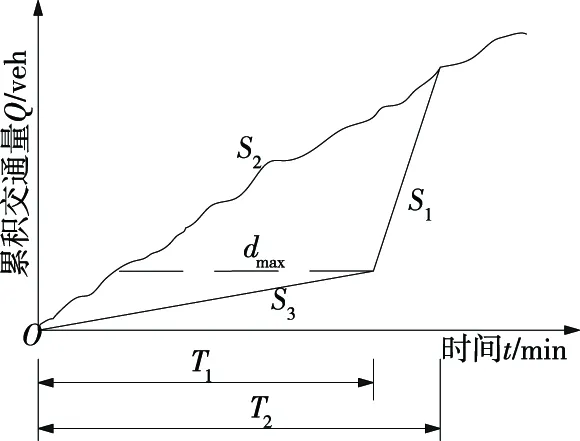
圖2 改進隊列法計算交通延遲示意圖

對式(1)～(4)進行修改以獲得準確的交通延遲計算結果。通過尋找到達曲線和離開曲線的交點(此時到達曲線的累積交通量為QT2)，得到T2：

(5)

由于到達曲線由離散采樣點連接而成，到達曲線與離開曲線的交點可能在2個采樣點之間。因此，采用簡單的線性插值法在2個采樣點之間的交點處增加1個虛擬采樣點，對應QT2和T2。

通過計算到達曲線和離開曲線圍合的面積，得到交通總延遲：

T1)2-S3T1(T2-T1)

(6)

式中：N為0～T2時段內采樣點數量(包括虛擬采樣點)；Qi為第i個采樣點對應的累積輸入交通量；Δti為到達曲線第i個采樣點對應的采樣間隔。

同理，作1條累積交通量等于S3T1的水平線，在該水平線與到達曲線的交點處采用線性插值法新增1個虛擬采樣點，該虛擬采樣點對應的累積交通量和時刻分別記為QT3、T3，則對于在時刻t流入事件地點的個體車輛，其時間延遲為：

(7)

式中：Q(t)為到達曲線在t時刻的累積輸入交通量。

由于到達曲線不再為直線，不能直觀判斷個體車輛的最大延遲。可基于式(7)計算的所有采樣點延遲按式(8)提取個體車輛的最大延遲。

dmax=max(di)；i=1,2,3,…,N

(8)

改進隊列法參照確定性隊列法進行計算，但引入到達曲線、事件持續時間和離開曲線的預測結果，既可參照確定性隊列法進行簡單計算，又能保證實時預測功能。若以若干分鐘為間隔進行更新，隨著時間的增長，即可提供更準確的實時預測結果。

3 算例分析

假設某快速路上發生交通事件并被及時發現，定義此時為零時刻。根據交通事件的性質、天氣狀況等，經線性回歸得到交通持續時間預測值T1=30 min。假設采樣間隔Δt=3 min，S1=6 000 veh/h，S3=2 000 veh/h。上游監測斷面的預測交通流量及其他相關數據見表1。

表1 上游監測斷面的預測交通流量及其他相關數據

根據表1中積壓交通量數據，在57～60 min存在1個虛擬采樣點(即到達曲線與離開曲線的交點)。經線性插值得到T2=57.15 min。根據式(6)得到總延遲Dtotal=30 837 veh·min，根據式(7)得到個體車輛在各輸入時刻的個體延遲dt，根據式(8)得到個體車輛最大延遲dmax=15.15 min。

1個采樣間隔后，根據上游監測斷面采集的輸入交通流數據更新Qup和Qa，根據下游監測斷面采集的輸入交通流數據更新S3、Qout和Qd，并更新交通事件影響消散時間T2、總延遲Dtotal、個體車輛延遲dt及個體車輛最大延遲dmax。以此類推，不斷實時更新交通延遲的預測值。

4 結語

確定性隊列法計算簡單，但只能用于事后的評估分析。隨機性隊列法能給出具有一定保證率的交通延遲預測結果，但計算較復雜。改進隊列法引入到達曲線、事件持續時間和離開曲線的預測結果，既可參照確定性隊列法進行簡單計算，又能提供實時預測功能，其實用性強，具有較大的應用潛力。