無砟軌道路橋過渡段動力分析

許思遙

(湖南省交通科學研究院有限公司，湖南 長沙 410014)

列車通過路橋過渡段時，因路基與橋臺剛度差異明顯，列車和線路振動加劇，導致過渡段受力環境復雜，容易發生軌道變形、扣件喪失剛度等，不利于列車安全運行及過渡段正常服役。針對該問題，李雙龍等以蒙華(浩勒報吉—吉安)重載鐵路為背景，建立輪軌-路基耦合模型，研究過渡段剛度及輪軌接觸力變化特性，認為倒梯形過渡段動力擴散效果優于一般路基；常文浩等以CRTSⅡ型板為研究對象，建立嚴寒地區路橋過渡段無砟軌道有限元模型，研究過渡段凍脹對過渡段的影響，認為過渡段長度較小時，凍脹變形會導致路橋過渡段層間離縫嚴重；李泰灃等建立輕質填料路橋過渡段模型，分析列車荷載作用下輕質填料路橋過渡段的動力響應，結果表明輕質填料路橋過渡段的動力性能滿足高速鐵路運營標準；周文濤等建立CRTSⅡ型板式無砟軌道路橋過渡段數值模型，計算列車和路橋過渡段的動力響應，認為隨過渡段不均勻沉降增大，過渡段列車和軌道的動力響應明顯增大，應嚴格控制過渡段不均勻沉降。為模擬列車-軌道-路橋過渡段真實工作狀態，并減少現場測量，該文以CRTSⅡ板式無砟軌道為研究對象，建立列車-軌道-路橋過渡段有限元模型，計算不同工況下列車與軌道的動力響應并分析其特性，為路橋過渡段優化設計提供參考。

1 列車-軌道-路橋過渡段模型構建

1.1 列車模型

列車以CRH3為研究對象，考慮車體、兩系懸架、轉向架及輪對。為提高計算效率并保證結果準確，適當簡化列車結構，車體、轉向架及輪對采用剛體模型(見圖1)。

圖1 列車模型

基于牛頓第二定律和動量矩理論建立列車動力方程：

(1)

式中：M、C、K分別為質量、阻尼和剛度矩陣；X為列車廣義位移向量；F為列車廣義荷載向量；t表示列車。

根據式(1)，利用ABAQUS多體動力模塊建立列車數值模型，列車的動力參數見表1，列車有限元模型見圖2。

表1 列車的動力參數

續表1

圖2 列車有限元模型

1.2 軌道模型

因輪軌相互作用較復雜，軌道模型采用連續分布模型，相關部件均采用實體單元。CRTSⅡ型板式無砟軌道由鋼軌、支撐層、CA砂漿及軌道板構成，軌道有限元模型見圖3。鋼軌模型(見圖4)采用60 kg/m鋼軌，相關參數見表2。

圖3 軌道有限元模型

圖4 鋼軌有限元模型

表2 鋼軌的截面尺寸及特性

扣件間距取0.6 m，亦為單節鋼軌長度。針對硬軌道振動特性，鋼軌單元尺寸取0.6 m。利用Merge將350個單節鋼軌合并，鋼軌總長度為210 m。為快速準確建模，利用MATLAB編寫子程序，批量建立Wire，模擬扣件形態。

1.3 路基模型

路基結構分3層，逐層填筑，基床上為壓實性級配碎石，底層為填料組A、B，路基采用壓實土。采用ABAQUS軟件建立路基有限元模型，路基采用C3D8R單元模擬，基本尺寸為500 m×13 m×5 m(長×寬×高)，邊坡坡度1∶1.5。路基結構剖面見圖5，有限元模型見圖6。

圖5 路基剖面(單位：m)

圖6 路基有限元模型

1.4 橋梁模型

以二跨箱形簡支橋梁為研究對象，單跨長30 m，其縱向剛度為400 kN/cm。橋梁相關參數見表3，橋梁剖面見圖7，有限元模型見圖8。

表3 橋梁的材料屬性

圖7 橋梁剖面(單位：m)

圖8 橋梁有限元模型

1.5 列車-軌道-路橋過渡段模型

過渡段形式為倒梯形，其模型見圖9。過渡段長度按式(2)計算，過渡段有限元模型見圖10。

圖9 路基-過渡段-橋梁連接剖面

圖10 軌道—路橋過渡段模型

L=a+(H-h)n

(2)

基于相關鏈接屬性，將上述模型在Assembly模塊中裝配。考慮列車與軌道輪軌的接觸關系，建立輪軌接觸屬性，模擬輪軌動態接觸。根據赫茲理論，輪軌接觸關系與輪軌接觸力、相對位移、接觸材料性質及接觸面形狀有關，將鋼軌和車輪視為圓柱體，由赫茲公式得：

y=Gp2/3

(3)

式中：y為輪軌法向相對位移；G為鋼軌撓度系數，其值為4.57R-0.149×10-8，車輪為磨耗性踏面時取3.86R-0.149×10-8，R為車輪半徑；p為輪軌法向接觸力。

輪軌接觸模型見圖11。

圖11 輪軌接觸模型

2 列車-軌道-路橋過渡段動力分析

2.1 列車運行安全性指標

高速鐵路規范采用列車運行安全性作為評價列車動力響應的主要依據，具體評價指標有脫軌系數和輪重減載率。

(1)脫軌系數。式(4)為脫軌系數表達式。根據文獻[5]，脫軌系數安全指標如下：H/F≤1.2為危險限度，H/F≤1.0為容許限度。

脫軌系數=H/F

(4)

式中：H為車輪橫向力；F為車輪縱向力。

(2)輪重減載率。式(5)為輪重減載率表達式。根據文獻[5]，輪重減載率安全指標如下：ΔP/P≤0.65為危險限度，ΔP/P≤0.60為容許限度。

輪重減載率=ΔP/P

(5)

式中：ΔP為輪重減載量；P為平均凈輪重。

2.2 列車運行平穩性評價指標

旅客乘車舒適度由列車運行平穩性來評價。采用列車垂向振動加速度和橫向振動加速度作為列車運行平穩性評價指標，評價標準見表4。

表4 列車振動加速度評價標準

2.3 軌道結構動力響應評價

由于橋梁和路基剛度不同，列車高速通過橋梁和路基連接部分會加劇輪軌沖擊作用，對軌道幾何形位、軌道結構穩定及路基結構產生不利影響。采用輪軌垂向力和輪軌橫向力評價高速鐵路路橋過渡段軌道結構的動力響應。

(1)輪軌垂向力。輪軌垂向力由輪軌垂向振動產生。為限制輪軌振動幅度，《高速試驗列車動力強度及動力學性能規范》規定，列車通過道岔、橋梁、曲線等部位時，最大垂向作用力不大于170 kN。

(2)輪軌橫向力Q。軌道結構存在軌道不平順、路基剛度不均勻等，會導致輪軌橫向力過大，引起軌道橫向變形、扣件損傷及列車脫軌。輪軌橫向力評價標準為Q≤43.8 kN。

3 動力特性分析

建立列車-軌道-路橋過渡段有限元模型，采用ABAQUS/Explicit求解器計算，分析不同過渡段長度和不同過渡段填料彈性模量下軌道和列車的動力響應。

3.1 過渡段長度對軌道動力響應的影響

依次計算不同過渡段長度下軌道垂向力和三向振動加速度等動力學指標，分析過渡段長度對軌道動力響應的影響，結果見圖12～15。

圖12 過渡段長度對輪軌垂向力的影響

由圖12可知：無過渡段時，輪軌垂向力為135.3 kN；輪軌垂向力隨著過渡段長度的增大逐漸降低，過渡段長度為15、20、25、30 m時，輪軌垂向力分別為124.4、123.1、122.9、122.9 kN。表明過渡段長度達到20 m后，繼續增加過渡段長度對降低輪軌垂向力無明顯作用。

由圖13可知：無過渡段時，輪軌垂向加速度為242g；輪軌垂向加速度隨著過渡段長度的增大逐漸降低，過渡段長度為15、20、25、30 m時，輪軌垂向加速度分別為222.5g、220.3g、218.5g、218.3g。表明過渡段長度達到20 m后，繼續增加過渡段長度對降低輪軌垂向加速度無明顯作用。

圖13 過渡段長度對輪軌垂向加速度的影響

由圖14可知：無過渡段時，輪軌橫向加速度為449.8g；橫向加速度隨著過渡段長度的增大略有降低，但衰減幅度并不明顯，與過渡段長度為20 m時相比，過渡段長度為30 m時橫向加速度僅降低0.20%。

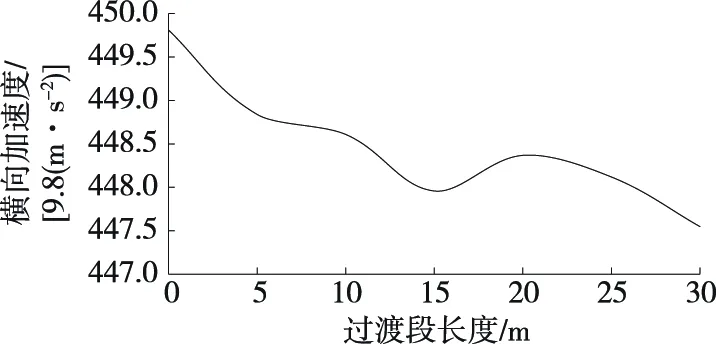
圖14 過渡段長度對輪軌橫向加速度的影響

由圖15可知：無過渡段時，輪軌縱向加速度為394.8g；縱向加速度隨著過渡段長度的增大趨于平緩；過渡段長度為20 m時，縱向加速度比無過渡段時降低0.33%。

圖15 過渡段長度對輪軌縱向加速度的影響

3.2 過渡段長度對列車動力響應的影響

依次計算不同過渡段長度下列車的輪重減載率、脫軌系數、車體垂向加速度，分析過渡段長度對列車動力響應的影響，結果見圖16～18。

圖16 過渡段長度對列車輪重減載率的影響

由圖16可知：無過渡段時，列車輪重減載率為0.638，大于容許限度；過渡段長度為5 m時，輪重減載率為0.546，小于容許限度；過渡段長度小于15 m時，隨著過渡段長度的增大，輪重減載率明顯降低；過渡段長度大于15 m時，隨著過渡段長度的繼續增大，輪重減載率無明顯變化。

由圖17可知：無過渡段時，脫軌系數為0.460；過渡段長度增加為20 m時，脫軌系數為0.235，比無過渡段時減小48.9%；過渡段長度大于20 m，繼續增加過渡段長度，脫軌系數變化不明顯。

圖17 過渡段長度對列車脫軌系數的影響

由圖18可知：無過渡段時，列車垂向加速度為0.138g；列車垂向加速度隨著過渡段長度的增加逐漸減小，過渡段長度達到20 m時列車垂向加速度為0.060g，比無過渡段時減小56.5%；繼續增加過渡段長度，列車垂向加速度變化不明顯。

圖18 過渡段長度對列車垂向加速度的影響

3.3 過渡段填料對軌道動力響應的影響

依次計算不同過渡段填料(填料不同彈性模量)下軌道三向振動加速度，分析過渡段填料對軌道動力響應的影響，結果見圖19～21。

圖19 過渡段填料對鋼軌垂向加速度的影響

由圖19可知：填料彈性模量為80～90 MPa時，鋼軌垂向加速度無明顯變化；填料彈性模量為90～120 MPa時，隨著填料彈性模量的增加，鋼軌垂向加速度逐漸減少，與填料彈性模量為90 MPa時相比，填料彈性模量為120 MPa時鋼軌垂向加速度減小22.43%，填料彈性模量在該范圍內對鋼軌垂向加速度有明顯影響；填料彈性模量為120～140 MPa時，鋼軌垂向加速度趨于平緩；填料彈性模量大于150 MPa時，鋼軌垂向加速度略有增加。

由圖20可知：填料彈性模量為80～120 MPa時，軌道板垂向加速度隨填料彈性模量的增加逐漸減小，與填料彈性模量為80 MPa時相比，填料彈性模量為120 MPa時軌道垂向加速度減小24.22%；填料彈性模量為120～150 MPa時，隨填料彈性模量增加，軌道板垂向加速度無明顯變化；填料彈性模量大于150 MPa時，軌道板垂向加速度略有上升。

圖20 過渡段填料對軌道板垂向加速度的影響

由圖21可知：填料彈性模量為80～90 MPa時，支撐層垂向加速度變化不明顯；填料彈性模量為90～110 MPa時，隨填料彈性模量增加，支撐層垂向加速度逐漸減小，與填料彈性模量為80 MPa時相比，填料彈性模量為110 MPa時支撐層垂向加速度減小15.6%；填料彈性模量大于110 MPa，隨著填料彈性模量的增大，支撐層垂向加速度無明顯變化。

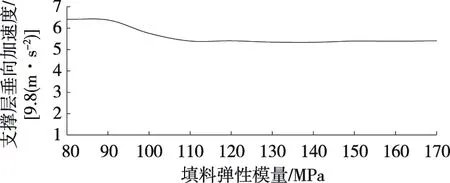
圖21 過渡段填料對支撐層垂向加速度的影響

3.4 過渡段填料對列車動力響應的影響

依次計算不同過渡段填料下列車的輪重減載率、脫軌系數、車體垂向加速度，分析過渡段填料對列車動力響應的影響，結果見圖22～24。

圖22 過渡段填料對列車輪重減載率的影響

由圖22可知：填料彈性模量為80～90 MPa時，列車輪重減載率無明顯變化；填料彈性模量為90～110 MPa時，隨填料彈性模量增大，列車輪重減載率逐漸降低，與填料彈性模量為90 MPa時相比，填料彈性模量為120 MPa時輪重減載率減小31.34%；填料彈性模量為110～150 MPa時，輪重減載率無明顯變化，趨于平穩；填料彈性模量大于150 MPa時，輪重減載率隨著填料彈性模量的增大而逐漸增大。

由圖23可知：列車脫軌系數隨填料彈性模量增加而逐漸減小；填料彈性模量為100～120、130～140 MPa時，脫軌系數趨于平緩；填料彈性模量為80、90 MPa時，脫軌系數較大，分別為0.469、0.464，均未超過容許限度。

圖23 過渡段填料對列車脫軌系數的影響

由圖24可知：填料彈性模量為80～120 MPa時，隨著填料彈性模量的增大，列車垂向加速度減小，與填料彈性模量為80 MPa時相比，填料彈性模量為120 MPa時列車垂向加速度降低58.62%；填料彈性模量為120～140 MPa時，列車垂向加速度趨于平緩；填料彈性模量大于150 MPa時，列車垂向加速度略有增加。

圖24 過渡段填料對列車垂向加速度的影響

4 結論

(1)路橋過渡段長度為0～20 m時，軌道和列車的動力響應隨著路橋過渡段長度的增大逐漸降低；過渡段長度大于20 m時，列車和軌道的動力響應隨著過渡段長度的繼續增大無明顯變化。

(2)隨著過渡段填料彈性模量的增大，列車脫軌系數逐漸減小；過渡段填料彈性模量為80～110 MPa時，其他動力響應隨填料彈性模量的增大逐漸降低；過渡段填料模量大于140 MPa時，列車動力響應增大。