面向智慧小鎮建設的機房電氣管線多目標優化布置方法

張 威

（北京北控京奧建設有限公司，北京102199）

北京延慶區作為2022年冬奧會的場地，需要以科學技術為背景，打造一個以綠色能源為中心，以物聯網智能感知技術為骨架的數字云小鎮。由于我國還沒有建設該類城鎮的經驗，因此在這個過程中，不可避免地需要重新設計電氣管線的排布，使其能夠適應物聯網感知技術的應用，并能夠在協調調配電力資源的基礎上，降低村鎮地下施工對電力系統與管線埋設的不良影響[1]。

文獻[2]總結分析了以往的電氣管線優化布置方法，以此提出了一個包括年平均管線損耗、管網彈性力比較、電力幅域加權平均值的指標分析，并將這些指標分別進行變量優化，構成了一個優化算法，但是這種算法缺乏有關于管線的電氣特性指標，難以與電氣布置相融合，實用性較差。文獻[3]將BIM 技術應用于建筑管線布置中，可以直觀展示管線綜合排布及機房局部布置，簡化了建筑電氣管線網絡的設計步驟，但該方法運算量較大，有待進一步完善。文獻[4]為了解決建筑環境中的多管道布局問題，設計了一種基于概率選擇生成的初始路徑管道，并采用協同進化和人工蜂群算法進行求解，研究了人工蜂群協同進化算法在多管道自動布局中的應用，但該算法只能針對單目標進行分析，無法解決過于復雜的問題。

本文基于以上文獻，基于多目標優化的算法，提出了一種機房電氣管線的布置方法，實現了對管線布置的安全性優化，并設計實驗，驗證該算法的性能優于常規的3 種算法。

1 設計機房電氣管線布置方法

1.1 設置電氣管線約束條件

在智慧小鎮內，由于地理環境的特殊性，能夠對電氣管線的安全性構成威脅的指標主要包括電壓均值、單位時間內電流量、電氣管線損耗恢復能力。設計機房電氣管線的布置優化方法，需要提前分析以上3 點指標的約束條件，并建立約束優化模型，式（1）～式（3）為這3 點約束指標的計算方法。

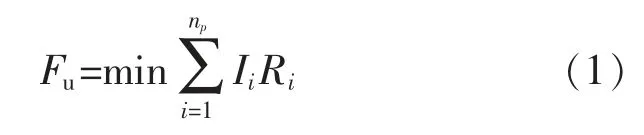
式中：Fu表示電壓均值在電氣管線優化布置中的適應度；np表示該模型中電氣管線的總數量，一般將其分為橫向管線與縱向管線2 種；Ii表示電氣管線的電流均值；Ri表示電氣管線的總電阻[5]。在計算以上電壓均值的過程中，需要綜合考慮管線所能夠承受的電流量與電線總電阻的問題，除此以外，管線長度也是可以影響電壓均值的指標之一。在計算單位時間內電流量時，可以通過式（2）計算其適應度。

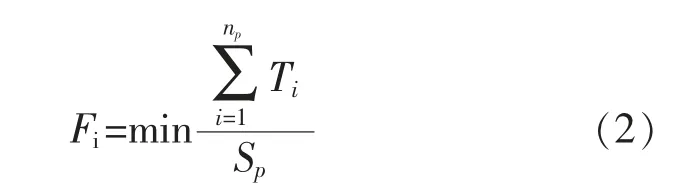
式中：Fi表示在單位時間內一段管線能夠流通的電流量的適應度；np表示該模型中電氣管線的總數量，一般將其分為橫向管線與縱向管線2 種[6]；Ti表示電氣流通管線對其造成的壓力；Sp表示管線的總長度，以米做單位[7]。電氣管線損耗恢復能力的適應度計算如式（3）所示。

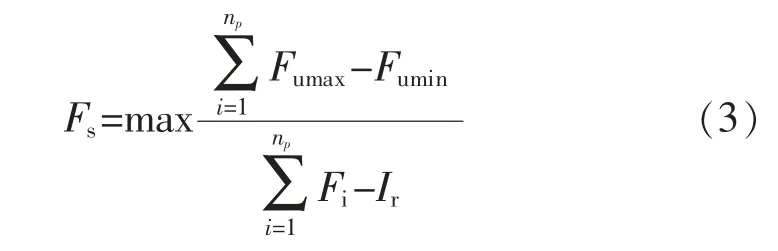
式中：Fs表示電氣運行時管線損耗恢復能力的適應度；Fumax表示電氣運行時管線的電壓均值最大值，其取值范圍為［0，1］；Fumin表示電氣運行時管線的電壓均值最小值，其取值范圍為［5，8］；Fi表示電氣運行時管線的電流量均值；Ir表示電氣運行時管線的電阻均值[8]。除此以外，還需要詳細設置管線之間的夾角系數、線頭松動指數、周邊土體平衡量等系數，使多目標規劃過程中的評價不會受到這些系數的干擾。

1.2 優化管線布置全局搜索

在設計電氣管線的多目標優化布置時，可以適當以安全性為基礎，約束電氣流速的平衡條件，保證其能夠處于正常值的范疇。在適應度函數中加入以上函數，以保證得到的算法能夠求得全局最優解。結合上文中設置的優化目標，可以得到管線優化的取值范圍為Si=｛S1，S2，…，Si｝[9]。其中，S1表示第一個優化的全局目標，以此類推Si表示第i個優化的全局目標。在針對性地進行目標優化時，可以適當使用編碼的方式進行管線直徑的計算與優化[10]，其編碼方式如圖1所示。

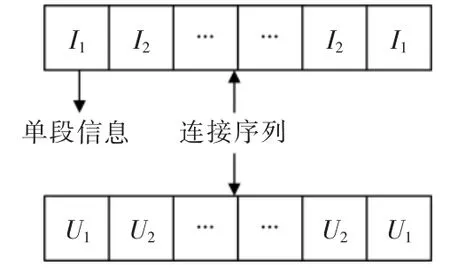
圖1 電氣管線優化編碼Fig.1 Optimal coding of electrical pipelines

如圖1所示，在電氣管線中設置初始的連接狀態，可以通過設定連接集解的方式，在雙序列的編碼中，I1和I2表示在該段電氣管線中電流信息編碼的具體信息[11]，U1和U2表示在該段電氣管線中電壓信息編碼的具體信息。在I1和I2之后，還有若干個電流信息編碼，直至編碼到Ii，再重新倒序編碼，返回到I2和I1[12]。電壓編碼中同樣如此，在U1和U2之后直至Ui，然后從Ui返回到U2和U1。這樣的編碼形式被稱為電氣管線的初始信息，也可以稱其為基因編碼。想要實現管線布置的全局搜索最優解，需要將以上編碼交叉操作，將其優點互相雜交，直至出現一種效率更高、條件更好的解，其交叉操作的方式如圖2所示。

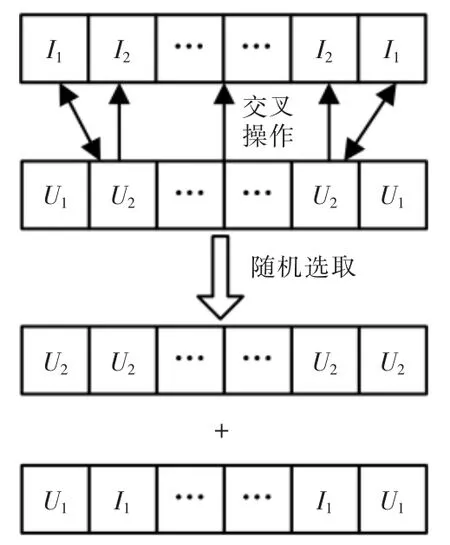
圖2 編碼交叉優化Fig.2 Coding cross optimization

如圖2所示，經過交叉編碼后，得到的編碼結構可能會發生優化現象，也有可能會出現回退現象，此時就需要將被優化后的編碼挑選出來，集中在一個外部檔案中，以便隨時查看與計算[13]。同時還可以將交叉過后的檔案集解通過種群迭代的方式傳遞到下一代，通過增加新個體的方式增強全局最優解的搜索效率。

1.3 建立多目標優化電氣管線模型

根據上文中的內容，設計智慧小鎮中機房電氣管線的多目標優化流程如圖3所示。

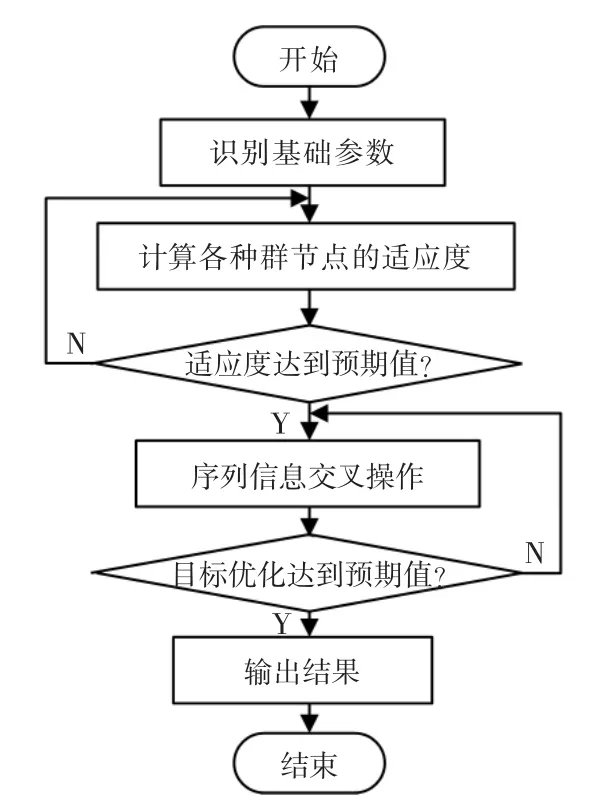
圖3 算法設計流程Fig.3 Algorithm design flow chart

綜上所述，想要實現多目標的機房電氣管線布置優化，就像也要根據以上約束條件建立規劃目標，同時通過管線模型實現目標函數的優化，其數學模型可以表示為

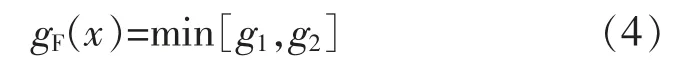
式中：g1和g2可以表示目標函數的約束條件。將其進行多目標優化的條件累計[14]，可以得到：

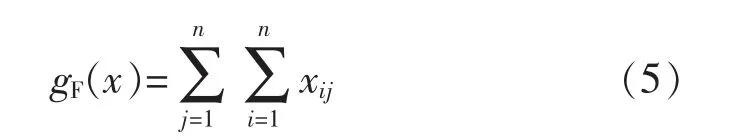
式中：xij表示從節點i到節點j中的管線參數，n表示管線的個數[15]。且通常情況下，當xij大于0 時，則表示從節點i到節點j存在多條管線，當xij等于0時，則表示從節點i到節點j存在一條管線，當xij小于0 時，則表示從節點i到節點j不存在管線。

2 實驗與分析

2.1 實驗準備

本實驗根據以上設計的多目標優化布置方法，對其在智慧小鎮機房中鋪設的電氣管線安全性能進行探究，并與常規的3 種方法相對比，判斷該多目標優化的方法是否存在安全性能的優化。將文中設計的多目標優化方法設置為實驗組，將常規的3種方法設置為對照組1～對照組3。在工程設計的軟件中設置20 根橫向與縱向的管線，其中兩兩一組，將橫向的管線設置為L 組，將縱向的管線設置為M組，并將其分別編號如圖4所示。

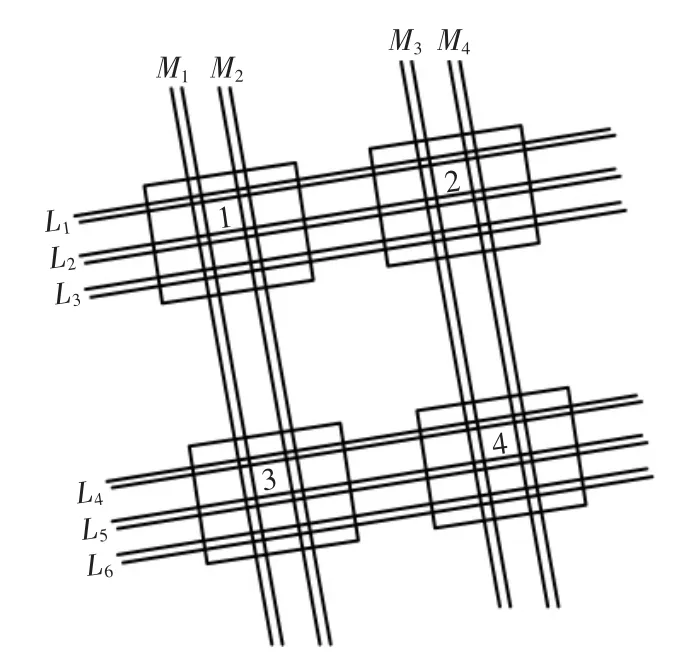
圖4 機房電氣管線鋪設簡圖Fig.4 Schematic diagram of electrical pipeline laying in machine room

如圖4所示，橫向管線與縱向管線交叉的集中區域為電氣管線的節點，本實驗共有4 個節點。在多目標優化的算法中設置初始種群數量為200，循環次數為1000，假設每次循環后向種群中添加10個新的個體。將以上1000 次循環實驗作為數據集，并在交叉驗證中分成若干個不同的組別，以N重交叉驗證的方式驗證該管線布置方法的解集優化程度。

2.2 算法測試

為了測試文中設計的多目標優化算法與常規的3 種算法的適應性，將其運用在機房電氣管線布置的實驗中，分別將以上數據集分為5 份與10 份，并計算其適應參數。

根據表1 和表2 中的測試結果可知，在五重交叉驗證中，實驗組數據集的平均適應度為47.776，而3 個對照組的平均適應度分別為41.932、40.386、40.462。在十重交叉驗證中，實驗組數據集的平均適應度為58.835，而3 個對照組的平均適應度分別為52.393、51.796、50.988。因此可知文中設計的多目標優化算法更好，能夠適應不同情況下的機房電氣管線布置，使項目施工更安全。

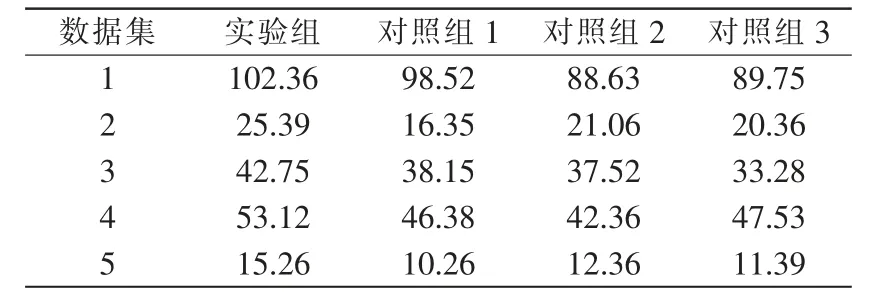
表1 五重交叉驗證Tab.1 Five-fold cross-validation

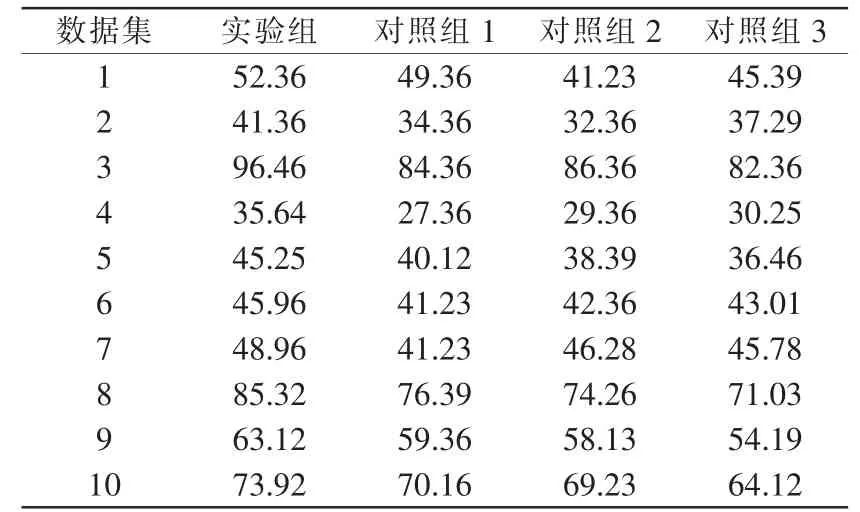
表2 十重交叉驗證Tab.2 Ten-fold cross-validation

2.3 機房電氣管線布置安全性測試

使用計算機計算在一切理想的前提下，圖3 中機房電氣管線布置完成后的安全指標，然后使用文中設計的多目標優化方法，得到該方法下的量化評價指標。接著將常規的3 種優化方法同樣應用在該目標下，得到如圖5所示的管線布置安全性測試結果。

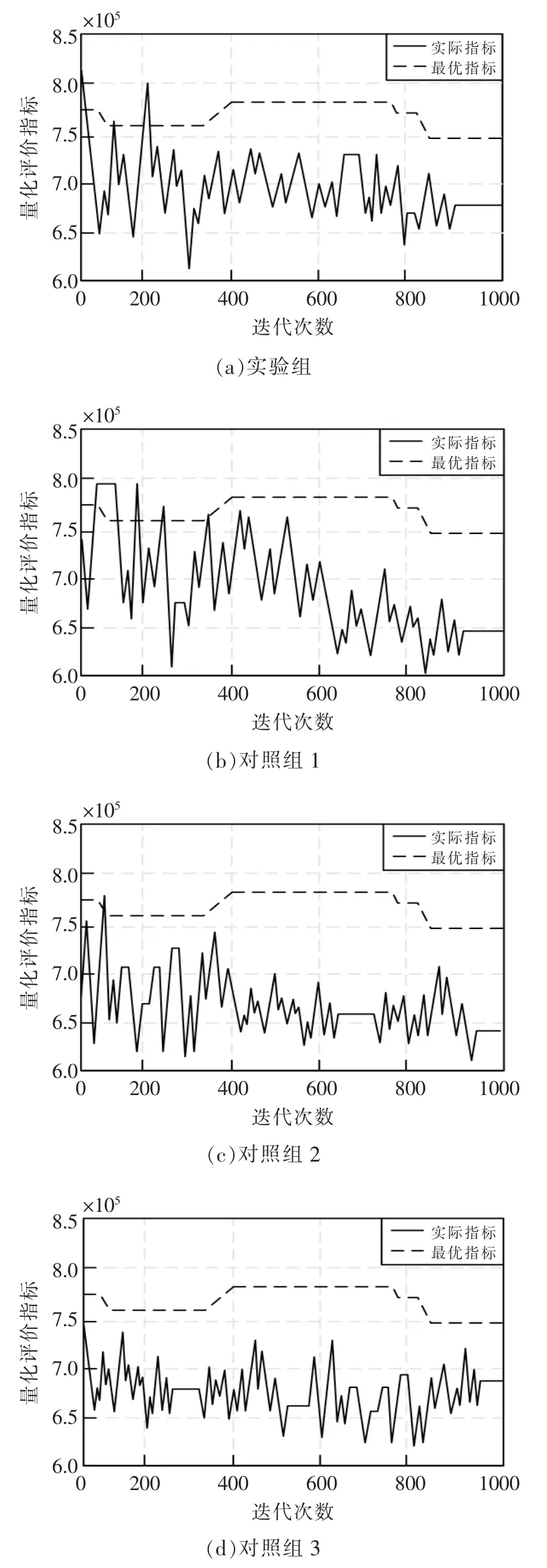
圖5 管線布置安全性測試Fig.5 Safety test of pipeline layout

根據圖5所示的管線布置安全性測試可知，量化指標在1000 次迭代中有著不同的結果，4 組實驗的實際指標與最優指標對比結果如表3所示。

如表3 可知，實驗組的平均量化指標最貼近最優指標，因此可以得到判斷：文中通過多目標優化算法得到的機房電氣管線布置方法擁有更好的安全性能，可以在工程施工時有更好的安全防護效果。

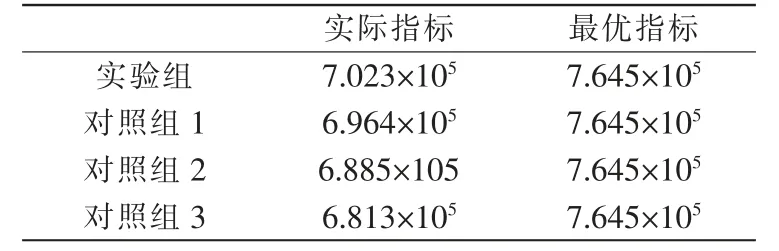
表3 結果對比Tab.3 Comparative results

3 結語

為了實現安全性能的提升，設計一個基于多目標優化的機房電氣管線布置方法，并設計實驗模擬該種方法在電氣管線工程中的作用。通過對比實驗可以得知，這類多目標優化的電氣管線布置算法優于常規的三種管線布置方法，能夠更貼合實際的管線布置工程。同時，其在實際應用時，安全性的量化指標也更貼合理論的最優指標。因此可知，該種基于多目標優化的管線布置方法實現了其優化目的，提高了管線布置的合理性與科學性。