山藥切片真空干燥特性及模型研究

張 欣，張 記，彭桂蘭，張宏圖，羅 森，楊 玲

（西南大學工程技術學院，重慶 400715）

山藥（Dioscorea oppositifoliaL.）屬于薯蕷科薯蕷屬植物，別名薯蕷、薯藥、山芋和懷藥等，其地下塊莖富含多糖、皂苷、蛋白質、氨基酸等多種功能性成分和營養成分，以及鈣、鐵、鋅、硒等微量元素，具有很高的藥用和食用價值[1]。但新鮮山藥含水率較高，在儲藏和運輸過程中易發生霉變和腐爛，造成較大的資源浪費和經濟損失。干燥是山藥儲藏的常用方法，通過去除部分水分、降低其水分活性，達到保持品質穩定和延長儲藏時間的目的。因此，山藥高效、高品質的試驗研究對山藥儲藏運輸、深加工以及提高產品附加值具有重要意義。

目前山藥干燥處理仍以熱風干燥和自然干燥為主，但自然干燥易受天氣影響，干燥效率低，且衛生安全不達標干燥品質差；熱風干燥具有生產能力大、生產效率高、操作方便和設備投資小等優點，但物料容易發生氧化和褐變。而真空干燥作為一種新興的綠色干燥技術，與常壓環境下的干燥方式相比，在節能、環保和干燥品質等方面具有較強優勢，近年來在果蔬干燥領域應用愈加廣泛。Orikasa等[2]分別研究了熱風干燥和真空干燥對獼猴桃片品質的影響，結果表明真空干燥可有效保留其抗壞血酸含量，獲得較高品質。孟國棟等[3]分別利用BP神經網絡模型和薄層干燥數學模型模擬花椒在真空干燥過程中的水分變化規律，發現BP神經網絡模型模擬精度更高。

干燥模型一直都是干燥研究的重點，建立干燥模型預測物料水分變化規律，對調控干燥過程和改進現有干燥系統具有重要意義。BP神經網絡模型具有較強的學習能力、識別能力以及建模簡單等特點[4]，Weibull分布函數具有覆蓋性廣、適應性強等特點[5]，目前已被廣泛用于預測物料在干燥過程中的水分變化規律，但是在山藥真空干燥中的應用研究尚未見報道。因此，本文對山藥切片進行真空干燥研究，探究干燥溫度、真空度和切片厚度對山藥切片真空干燥特性的影響，分別利用BP神經網絡模型和Weibull分布函數擬合水分比曲線，建立相應模型并進行試驗驗證，計算有效水分擴散系數和干燥活化能，以期為山藥真空干燥水分比預測、工藝優化等提供理論依據。

1 材料與方法

1.1 材料與儀器

新鮮鐵棍山藥 2020年9月收購于河南省焦作市溫縣，購回后選擇粗細均一，無破損、霉變和腐爛的山藥置于4±1 ℃的冰箱中冷藏儲存，并根據GB 5009.3-2016《食品中水分的測定》[6]中的直接干燥法測得其初始含水率為71.12%。

202-00型電熱恒溫干燥箱 上海光地儀器設備有限公司；KW-2型旋片式真空泵、DZF-2AS型真空干燥箱 北京科偉永興儀器有限公司；YP-6002B型電子天平 精度0.01 g，上海力辰儀器科技有限公司；HH-2型數顯恒溫水浴鍋 精度0.1 ℃，常州越新儀器制造有限公司；NR60CP型多功能色差儀 深圳市三恩時科技有限公司；KAL-10A型電力監測儀上海希崖電子有限公司；SJ-455515型游標卡尺 海寧上匠工具有限公司；GZM-2100型切片機 任丘市格芝美電子商務有限公司；50目分樣篩 直徑20 cm，紹興市上虞區豪泉篩具廠。

1.2 實驗方法

1.2.1 真空干燥工藝流程 新鮮山藥→清洗（泥污）→除雜（根須）→去表面水分→去皮→切片→干燥→指標測量→封裝

1.2.2 真空干燥試驗 在前期預實驗的基礎上，選取干燥溫度40、50、60、70、80 ℃；真空度0.03、0.04、0.05、0.06、0.07 MPa；切片厚度2、4、6、8、10 mm進行干燥試驗。每次試驗提前30 min開啟真空干燥箱，調至預設溫度進行預熱，同時將山藥從冰箱中取出，使其恢復至室溫，然后再進行清洗、除雜、去皮和切片等操作，待真空干燥箱達到穩定溫度后，稱取50±0.5 g山藥片均勻平鋪于分樣篩中（單層），然后放入真空干燥箱中開始干燥。干燥過程中每隔15 min將試樣快速取出稱量，記錄質量數據，直至試樣含水率低于安全含水率17%[7]時停止干燥。每組試驗重復3次，試驗數據取平均值。

1.2.3 試驗指標測定

1.2.3.1 干基含水率 干基含水率按式（1）計算[8]：

式中：Mt表示試樣在t時刻的干基含水率，g/g；mt表示試樣在t時刻的質量，g；md表示試樣的絕干物質質量，g。

1.2.3.2 水分比MR 水分比按式（2）計算[9]：

式中：MR表示試樣在t時刻的水分比，無量綱；Me表示試樣達到平衡時的干基含水率，g/g；M0表示試樣的初始干基含水率，g/g。

對于時間較長的干燥過程，試樣的平衡含水率Me遠小于其初始含水率M0和t時刻含水率Mt，可忽略不計，因此可采用簡化公式（3）來計算水分比[10]。

1.2.3.3 干燥速率DR 干燥速率按式（4）計算[11]：

式中：DR表示試樣在t時刻的干燥速率，g/（g·min）；Mt+Δt表示試樣在t+Δt時刻的干基含水率，g/g。

1.2.3.4 有效水分擴散系數Deff絕大多數生物材料的干燥過程都屬于降速干燥過程，水分遷移主要由內部擴散控制，因此可用菲克第二擴散定律來描述，對于時間較長的干燥過程，可進一步簡化為[12]：

式中：Deff表示有效水分擴散系數，m2/s；t表示干燥時間，s；L表示試樣切片厚度，m。

有效水分擴散系數的估算值Dcal可按照式（6）進行計算[13]：

式中：Dcal表示有效水分擴散系數估算值，m2/s；Deff與Dcal之間的關系可用幾何參數Rg來表示，其計算公式如下：

1.2.3.5 干燥活化能Ea干燥活化能、有效水分擴散系數以及干燥溫度三者之間的關系可用阿倫尼烏斯公式來描述，其表達式如下[14]：

式中：D0表示指數前因子，m2/s；R表示理想氣體常數，kJ/（mol·K）；Ea表示活化能，kJ/mol；T表示干燥溫度，℃。

1.2.4 BP神經網絡模型 BP神經網絡由輸入層、隱含層、輸出層和各層神經元連接而成，確定各層神經元節點數，即可建立山藥切片真空干燥的BP神經網絡模型。

1.2.4.1 輸入層和輸出層節點的確定 選擇溫度、真空度、切片厚度和干燥時間作為輸入層節點，將不同時刻山藥切片的水分比作為輸出層節點，即輸入層節點數為4，輸出層節點數為1。輸入和輸出數據按照公式（9）進行歸一化處理。

式中：Xnorm表示歸一化后的數據值；Xi表示原始數據值；Xmax、Xmin表示原始數據中最大和最小值。

1.2.4.2 隱含層節點數的確定 理論證實BP神經網絡在不限制隱含層節點數的情況下，只需一個隱含層就可實現輸入到輸出的非線性映射，因此采用單隱含層，節點數可以按照經驗公式（10）確定[15]：

式中：m表示隱含層節點數目；a表示輸入層節點數目；b表示輸出層節點數目；n表示調節常數，取值范圍1～10之間。

本文中的a、b分別為4和1，則根據公式（10）可知本文神經網絡的隱含層節點數m在3～13范圍之內。將通過對不同隱含層節點數的神經網絡進行訓練，根據其訓練結果優劣來進一步確定最優的隱含層節點數。

1.2.4.3 函數和算法的選擇 本文BP神經網絡的隱含層傳遞函數為Tansig函數，輸出層傳遞函數為Purelin函數。Levenberg-Marquardt算法在迭代過程中能自適應地改變下降梯度，具有較快的收斂速度和較好的性能，因此采用LM算法對神經網絡進行訓練。

1.2.5 Weibull分布函數 Weibull分布函數表達式，如下所示[10]：

式中：α表示尺度參數（表示干燥過程中的速率常數，約為物料脫去63%水分所需時間），min；β表示形狀參數（與物料水分遷移機制有關）；t表示干燥時間，min。

1.3 數據處理

模型對試驗數據的擬合優劣程度可根據決定系數R2、卡方χ2、均方根誤差RMSE來評價。模型的R2值越高，χ2和RMSE值越低，則說明該模型對試驗數據的擬合效果越好。各評價指標可按式（12）～（14）計算[16]：

式中：MRpre,i、MRexp,i表示水分比模型預測值和試驗值，無量綱；表示水分比模型預測值的平均值；N表示該組試驗所獲得的數據個數；z表示模型中的常數個數。

2 結果與分析

2.1 山藥切片真空干燥特性分析

2.1.1 溫度對山藥切片真空干燥過程的影響 當真空度為0.05 MPa、切片厚度為4 mm時，不同溫度條件下山藥切片的真空干燥特性曲線如圖1所示。

圖1 不同溫度條件下山藥切片真空干燥特性曲線Fig.1 Vacuum drying curves of yam slices at different temperatures

由圖1中的水分比曲線可知，將山藥切片干燥至安全含水率所需時間會隨著溫度的升高而逐漸縮短。在40、50、60、70和80 ℃條件下所需干燥時間分別為825、555、375、270和210 min，由此可見溫度越高，干燥時間越短，提高溫度可顯著縮短干燥時間（P=7.56×10-11＜0.01），其原因是溫度越高，相同時間內山藥片可獲得更多的熱量，使水分子運動加劇，加快水分蒸發[10]。由圖1中的干燥速率曲線可知，干燥開始后干燥速率將在短時間內迅速達到最大值，且溫度越高其值越大，在40、50、60、70和80 ℃條件下的最大干燥速率分別為0.00359、0.00613、0.00816、0.01092和0.01361 g/（g·min），而后干燥速率將隨著時間的延長不斷降低直至干燥結束，在所有溫度條件下均未觀察到明顯的恒速干燥階段。此外，李暉等[17]在山藥切片的熱泵干燥研究中，以及樊迎等[18]在山藥切片的熱風干燥研究中均發現溫度對干燥時間影響顯著，溫度越高所需干燥時間越短，與本文所得結論相一致。

2.1.2 真空度對山藥切片真空干燥過程的影響 當溫度為60 ℃、切片厚度為4 mm時，不同真空度條件下山藥切片的真空干燥特性曲線如圖2所示。

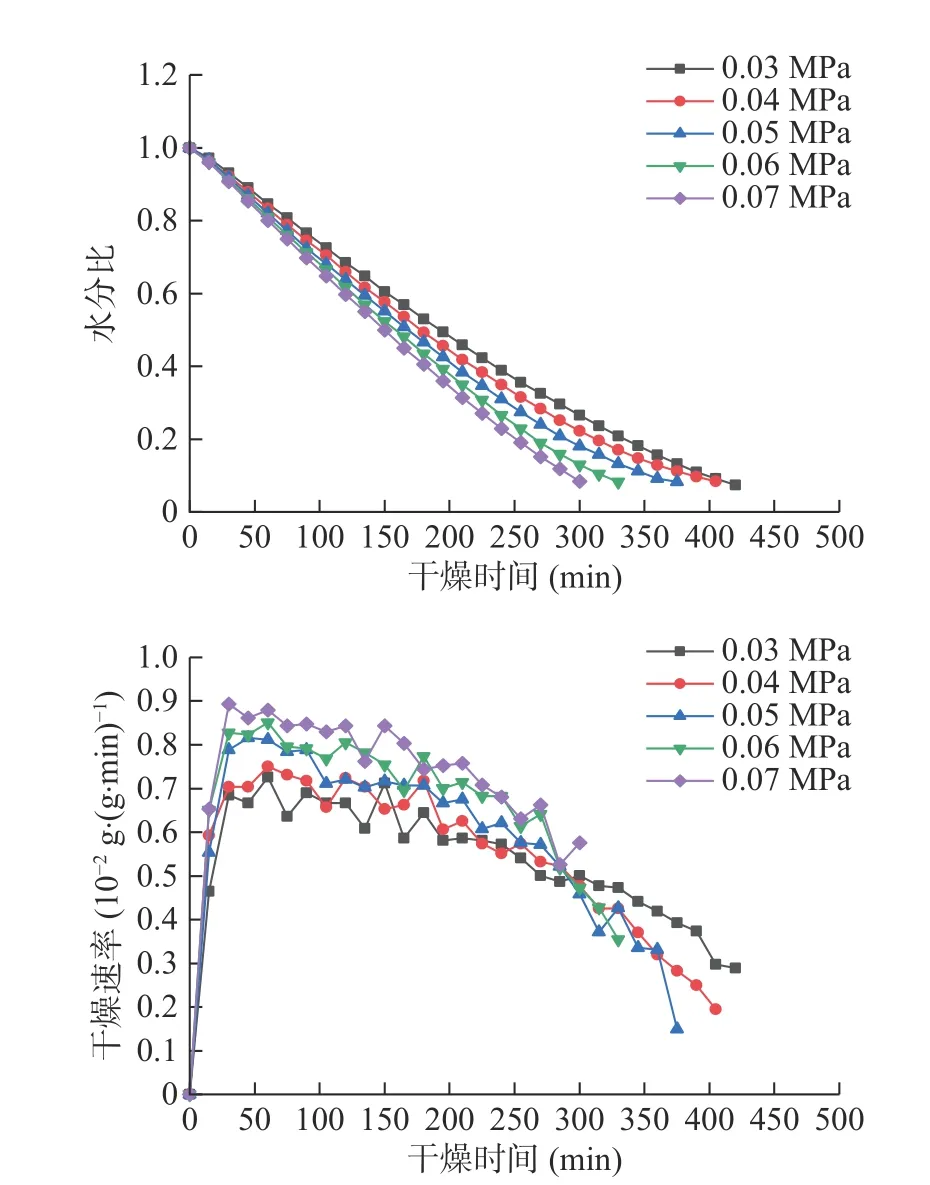
圖2 不同真空度條件下山藥切片的真空干燥特性曲線Fig.2 Vacuum drying curves of yam slices at different vacuum pressure

由圖2中的水分比曲線可知，真空度升高，干燥時間逐漸縮短。在0.03、0.04、0.05、0.06和0.07 MPa條件下所需干燥時間分別為420、405、375、330和300 min，由此可見真空度對干燥時間影響不顯著，其原因是雖然真空度升高可以使水的沸點降低、加快蒸發，但同時也會對傳熱造成影響。陳健凱等[19]和張樂等[20]也得出與本文相似結論。由圖2中的干燥速率曲線可知在所有真空度條件下均未觀察到明顯的恒速干燥階段，屬于降速干燥過程。0.03、0.04、0.05、0.06和0.07 MPa條件下的最大干燥速率分別為0.00726、0.00750、0.00816、0.00850和0.00893 g/（g·min），真空度增加0.04 MPa，最大干燥速率僅增加了23.00%，可見真空度的改變并不會對干燥速率造成顯著影響（P=0.32＞0.05）。

2.1.3 切片厚度對山藥切片真空干燥過程的影響當溫度為60 ℃、真空度為0.05 MPa時，不同切片厚度條件下山藥切片的真空干燥特性曲線如圖3所示。

圖3 不同切片厚度條件下山藥切片的真空干燥特性曲線Fig.3 Vacuum drying curves of yam slices at different thickness

由圖3中的水分比曲線可知，干燥時間隨著切片厚度的增加而逐漸延長。在2、4、6、8和10 mm條件下所需干燥時間分別為255、375、495、630和720 min，切片厚度從2 mm增加至10 mm相應的干燥時間延長了182.35%。由此可見切片厚度對干燥時間影響顯著（P=1.82×10-6＜0.01），減小切片厚度可顯著縮短干燥所需時間，其原因是切片厚度越薄，水分遷移的距離就越短，水分能夠及時從山藥切片內部遷移至其表面，然后蒸發去除[21]。此外，Doymaz等在柿子切片[11]和胡蘿卜切片[9]的熱風干燥研究中也發現與本文相似結論，即干燥時間隨切片厚度減小而縮短，物料厚度越薄干燥越快。

由圖3中的干燥速率曲線可知，不同切片厚度條件下的干燥速率曲線變化趨勢基本一致，均只有短暫的升速和較長的降速干燥階段，無明顯恒速干燥階段。在2、4、6、8和10 mm條件下的最大干燥速率分別為0.01150、0.00816、0.00640、0.00529和0.00493 g/（g·min），結合干燥曲線可知在8和10 mm條件下的干燥速率并無明顯差異，其原因是該厚度條件下的山藥切片在干燥中后期其內部水分向表面遷移的速率遠小于表面水分的蒸發速率，導致其內外應力分布不均而發生皺縮，甚至上下表面向內凹陷。這導致其內部孔隙減少，質地更為緊密，使水分的遷移受到嚴重阻礙。

2.2 BP神經網絡模型的建立

由公式（10）可知，本文BP神經網絡模型的隱含層節點數在3～13范圍之內，將13組試驗數據共399個數據點作為BP神經網絡的訓練數據，對不同隱含層節點數的BP神經網絡進行訓練，其訓練結果見表1。由表1可知節點數為11和13時，R值最高，均為0.99997，但節點數為11時，MSE值最低，因此本文BP神經網絡的隱含層節點數選擇為11。

表1 不同隱含層節點數的訓練結果Table 1 Training results of neural network with different hidden nodes

輸入層節點數為4，隱含層節點數為11，輸出層為1層，因此神經網絡結構為4-11-1，神經網絡拓撲結構確定為如圖4所示。

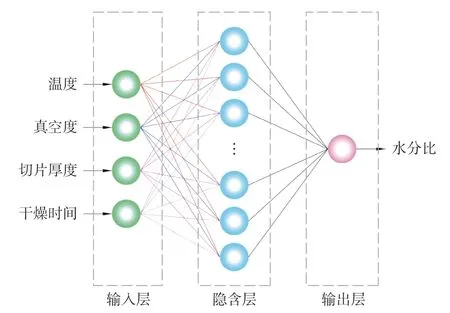
圖4 神經網絡的拓撲結構Fig.4 Topology of the neural network in this study

隱含層節點數為11、傳遞函數依次為Tansig函數和Purelin函數時的MSE值變化曲線、水分比預測值和試驗值的擬合情況及相關系數見圖5，左圖中圓圈標記迭代155次后達到設定的訓練精度。

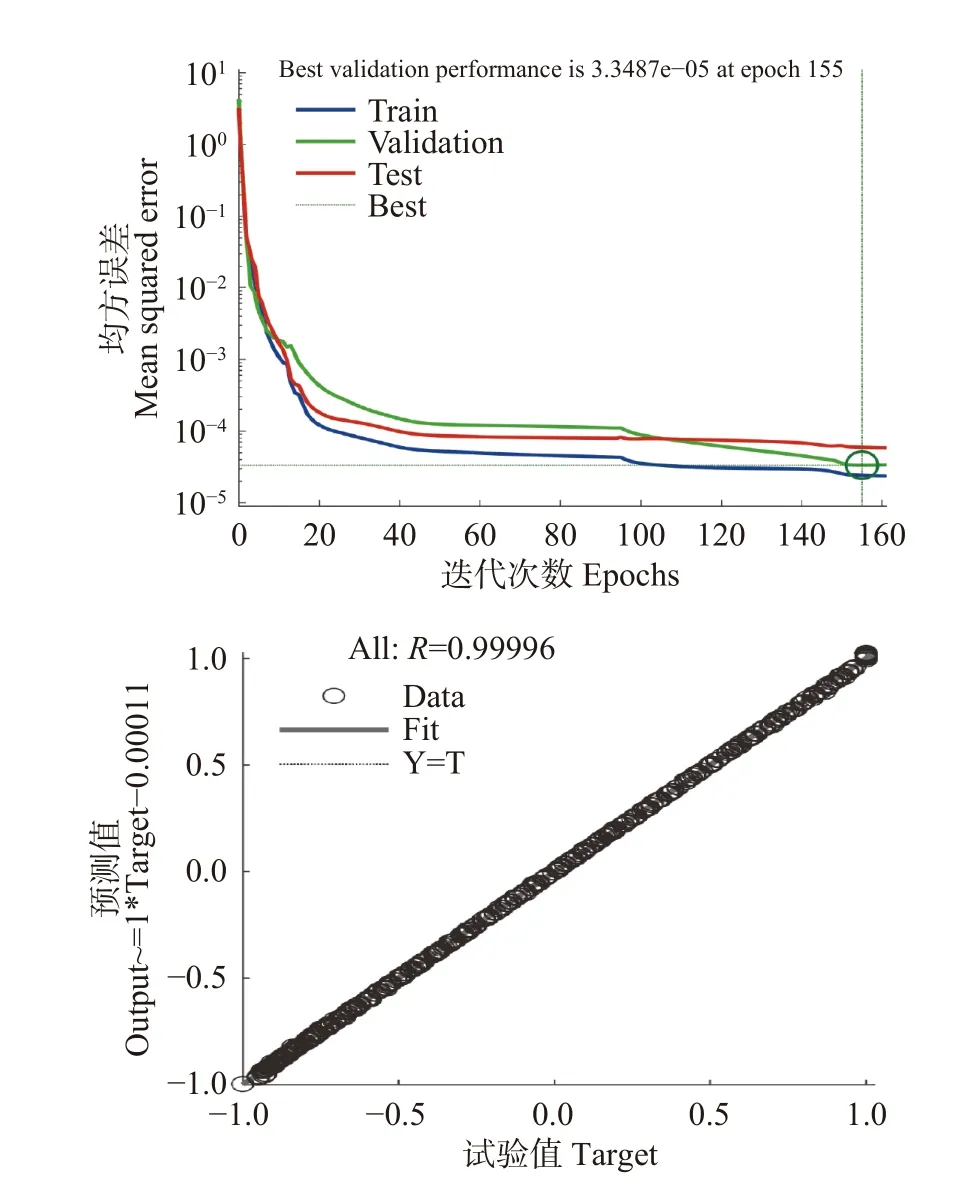
圖5 神經網絡訓練結果Fig.5 Neural network training results

本文BP神經網絡輸入層與隱含層，隱含層與輸出層間之間的權重矩陣分別為：

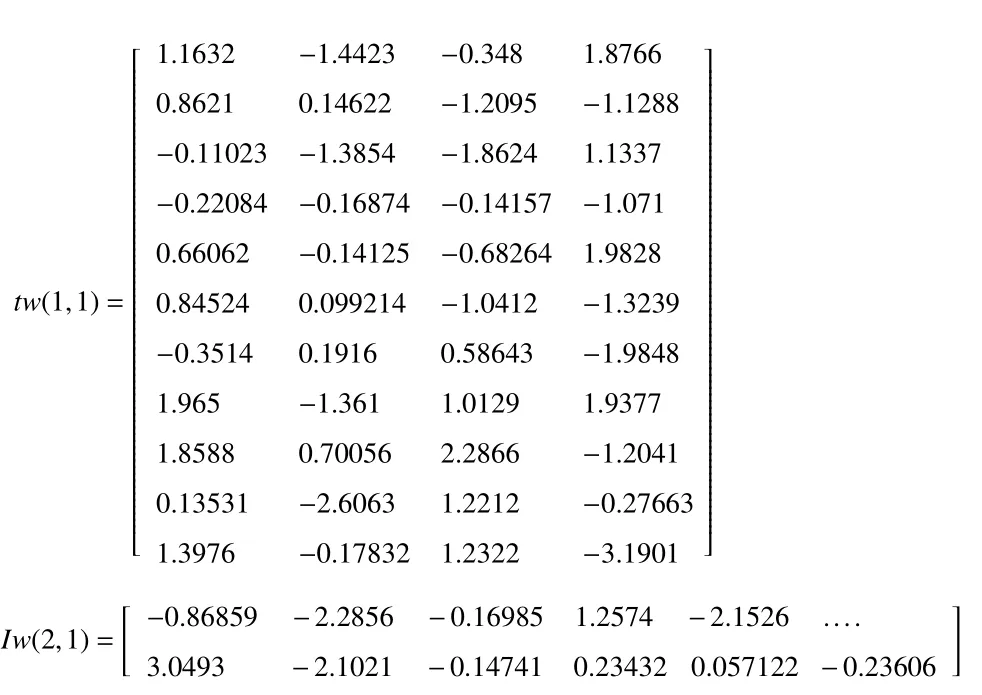
輸入層與隱含層，隱含層與輸出層之間的閥值向量分別為：

2.3 基于Weibull分布函數分析山藥切片真空干燥過程

2.3.1 尺度參數α由表2可知，在不同干燥條件下，尺度參數α的值在120.499～480.519 min的范圍內變化。真空度為0.05 Mpa，切片厚度為4 mm時，尺度參數在80和40 ℃分別取得最小值120.499 min和最大值480.519 min，可以看出溫度對尺度參數α的影響很大，隨著溫度的升高，尺度參數α減小。當溫度為60 ℃，真空度從0.03到0.07 MPa時，尺度參數α的值從241.311 min僅降低至184.714 min，差值不大，說明山藥切片干燥過程中真空度對尺度參數α的影響不顯著。當溫度和真空度一定時，切片厚度從2 mm增加至10 mm，尺度參數α從145.135 min增加至379.654 min，增加了61.77%，說明切片厚度對尺度參數α值影響較大。由上述可知，提高溫度、減小切片厚度均有利于干燥時間的縮短。

2.3.2 形狀參數β形狀參數β和干燥過程中物料內部水分遷移機理相關[22]，反映了干燥速率變化。當形狀參數β＞1時，物料水分擴散機制為內外部共同控制，物料在干燥前期存在延滯階段，即干燥速率先上升后下降。由表2可知，在不同干燥條件下形狀參數β為1.3172～1.5204，均大于1，說明山藥切片在干燥前期存在延滯階段，與前文所得特性一致，進一步說明Weibull分布函數可以用來描述山藥切片真空干燥過程。另外，從表2中可以看出，溫度增加時，形狀參數β的值隨之增加，說明形狀參數β受溫度影響較大，切片厚度發生變化時，形狀參數β也有一定程度的改變，說明形狀參數β是一個與被干燥物料形狀相關的參數，而真空度對形狀參數β的值影響不明顯。

表2 Weibull模型擬合結果Table 2 Weibull model fitting results

2.3.3 Weibull模型的建立 以尺度參數α和形狀參數β作為因變量，溫度T、真空度V和切片厚度L作為自變量。按照式（15）、（16）對Weibull模型參數進行一次多項式擬合。

式中：a0、a1、a2、a3和b0、b1、b2、b3是待求多項式系數。

利用OriginPro2017軟件進行多元線性回歸分析得：

將式（17）、（18）代入式（11）可得山藥切片真空干燥的Weibull模型方程為：

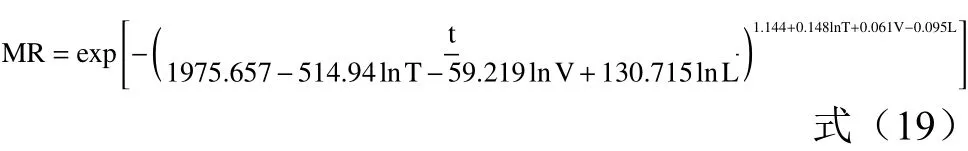
2.4 BP神經網絡模型和Weibull分布函數的驗證

為了驗證所建立的BP神經網絡模型以及Weibull分布函數模型的準確性，另增加1組驗證試驗，試驗條件為：70 ℃、0.05 MPa、6 mm。驗證試驗的水分比試驗值與模型預測值的對比結果見圖6，由圖可知水分比試驗值與預測值之間具有較好的一致性，BP神經網絡模型以及Weibull分布函數模型的平均相對誤差ER為3.08%和10.7%，這表明所建立的BP神經網絡模型對山藥切片在真空干燥過程中的水分變化規律具有更好的預測能力。

圖6 神經網絡模型水分比預測值與試驗值對比Fig.6 Comparison of experimental value and predicted value of moisture ratio

2.5 有效水分擴散系數Deff的分析

由公式（5）可知，lnMR與干燥時間t呈線性關系，利用OriginPro 2017軟件對不同干燥條件下的lnMR和t進行線性回歸分析，線性回歸分析及計算結果見表3。

由表3可知，有效水分擴散系數在4.0042×10-9～3.4652×10-8m2/s之間，溫度從40 ℃增加至80 ℃，真空度從0.03 MPa增加至0.07 MPa，切片厚度從2 mm增加至10 mm，相應的有效水分擴散系數分別增大了4.43、1.3、8.65倍，說明溫度和切片厚度對有效水分擴散系數影響較大，而真空度對有效水分擴散系數影響較小。切片厚度越薄，Deff值越小，可能是由于厚度較薄的物料失水速率較快，其表面容易硬化，阻礙了內部水分向表面遷移，從而導致水分有效擴散系數較小，與白冰玉等[23]的結果類似。如表3所示，山藥切片真空干燥的幾何參數Rg值在1.0702～1.2669，接近1，說明估算水分擴散系數Dcal和有效水分擴散系數Deff的值很接近，同時決定系數R2均在0.91以上，表明擬合結果很好，計算出的有效水分擴散系數很可靠，也說明由Weibull函數估算的水分擴散系數的值可靠性高。

表3 不同干燥條件下的有效水分擴散系數Table 3 Effective diffusivity coefficient under different drying conditions

2.6 干燥活化能分析

由上文可知，lnDeff與1/（T+273.15）呈線性關系，進行線性回歸分析得到的山藥切片真空干燥的活化能為33.802 kJ/mol，處于一般農產品的活化能范圍之內[24]（12.7～110 kJ/mol），這表明山藥切片在真空干燥去除1 mol水分所需要的能量為33.802 kJ，干燥較為容易。湯尚文等[25]在山藥紅外干燥研究中得到活化能為30.269 kJ/mol，與本文所得結果較為接近，說明山藥真空干燥和紅外干燥的難易程度處于同一水平，均較易實現。

3 結論

本文研究了山藥切片的真空干燥特性，應用Weibull分布函數和BP神經網絡對不同干燥條件下的試驗數據進行擬合分析，結果表明：山藥切片真空干燥過程只存在升速和降速干燥階段，無明顯恒速干燥階段，屬于典型的降速干燥過程。溫度越高，切片厚度越小，干燥速率越快，所需干燥時間則越短。不同干燥條件下的有效水分擴散系數Deff在4.0042×10-9～3.4652×10-8m2/s之間，隨著溫度和切片厚度的增加而增加，真空度對其影響不顯著。山藥切片真空干燥的活化能為33.802 kJ/mol，處于一般農產品的活化能范圍之內，這表明山藥切片的真空干燥較為容易。

利用Weibull分布函數和BP人工神經網絡進行分析時，驗證試驗結果表明BP神經網絡模型更適合用來描述山藥切片真空干燥過程。本試驗僅對山藥切片真空干燥特性、動力學模型進行了研究，后續可進一步研究其干燥品質或最優干燥參數或干燥條件對其功能性成分含量的影響。