電梯柔性提升系統橫向-縱向耦合動力學建模與仿真*

殷銘豪 吳 曉，2 曹 丹 田健康 徐家根

1西南交通大學機械工程學院 成都 610031 2軌道交通運維技術與裝備四川省重點實驗室 成都 610031

0 引言

以鋼絲繩、鋼纜等作為提升載體的礦井提升機、曳引電梯、起重機等可統稱為柔性提升系統，隨著系統的運行，提升系統的剛度、質量、阻尼等參數不斷發生變化[1，2]。國內外學者通常將該類結構轉化為一端固定的軸向運動弦線[3，4]。高速運行過程中的系統對外界的干擾激勵敏感，易發生振動，降低系統壽命甚至影響安全使用[5-7]。

國內外學者對柔性提升系統進行了一系列研究。Yong B G等[8，9]對摩擦提升系統中鋼絲繩動力學及摩擦傳遞的耦合關系進行建模，分析系統橫向振動的影響因素；郭瑜等[10]建立塔式摩擦提升系統動力學模型，分析該提升鋼絲繩與尾繩的縱向振動；吳娟等[11]建立多繩摩擦提升系統，分析不同運行階段對系統橫向振動的影響；齊秀娟[12]建立高速曳引電梯橫向振動模型，推導了曳引鋼絲繩橫向剛度公式，分析了曳引鋼絲繩的最小剛度與位置；Zhang C Y等[13]建立了靜止時電梯系統的集中參數離散模型，分析了系統發生振動的原因；Young M等[14]將電梯系統中鋼絲繩視為多個帶質量的彈簧阻尼器，建立了集中參數的多自由度模型；Lee Y M等[15]和Kang J K等[16]以電梯系統為研究對象，建立系統離散模型，提出一種可抑制電梯轎廂垂直振動的控制策略；馮子朔[17]建立考慮曳引輪兩側轎廂與對重的相互作用與曳引鋼絲繩長度變化的離散模型，分析了不同因素對曳引電梯運行及制動的影響。

將柔性提升系統簡化為集中參數的離散模型，忽略了系統運行過程中提升鋼絲繩的參數變化，系統低速運行時，鋼絲繩的慣性影響較小，可高效分析該類系統的動力學特性，但是當系統高速運行時，運行狀態參數變化較快，故提升鋼絲繩對系統的振動影響不容忽視。本文基于能量法和Hamliton原理建立柔性提升系統橫向-縱向耦合振動方程，考慮系統懸掛平衡繩以及實際受力影響，使用Matlab軟件分析系統有平衡繩與無平衡繩時的振動響應，分析導軌不平順激勵對系統振動的影響。

1 柔性軸向運動系統振動控制模型

變長度軸向運行系統如圖1a所示，懸掛重物之間采用平衡繩連接，將該系統簡化為如圖1b所示的柔性軸向運動系統，重物之間的平衡繩以圖1所示張緊繩與彈簧阻尼器模擬，張緊繩的狀態由張緊輪控制。導靴裝置簡化為重物與導軌之間的彈簧阻尼器，其剛度為k1，阻尼為c1，提升鋼絲繩的長度為l(t)，線密度為ρ1，分布阻尼為c，t時刻x處的橫向振動與縱向振動分別為w(x，t)和u(x，t)，下端張緊繩的長度為H-l(t)，線密度為ρ2，H為建筑高度。為分析系統頂端曳引輪對系統的影響，假設頂端存在橫向激勵e1(t)。

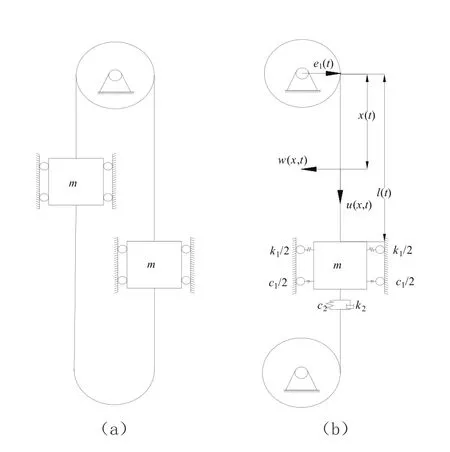
圖1 柔性軸向運行系統簡化模型

本文中模型的建立原則為：1）忽略井道內空氣氣流與張緊繩振動的影響；2）提升鋼絲繩縱向振動與橫向振動的變形數值均遠小于系統的長度；3）系統運行過程中鋼絲繩的各項結構參數不會發生變化。

系統運行過程中提升鋼絲繩x處的位移R與速度V為

當x=l(t)時，式（1）為重物的位移與速度，微分算子為

由式（1）可得系統的動能為

為方便表達，下文將使用u和w分別表示系統t時刻x處的縱向振動與橫向振動，下標x與t分別為對其求偏導。

提升鋼絲繩x處的張緊力為

式中：F為保持張緊狀態的張緊力。

運行過程中系統的勢能為

式中：ε為鋼絲繩的正應變[18]，k為鋼絲繩的曲率[19]。

系統中阻尼做的虛功為

由Hamliton原理，將系統的動能、勢能、虛功代入可得

系統運行過程中的邊界條件為

將式（8）整理可得系統的橫向-縱向振動偏微分方程。

由于頂端曳引輪橫向激勵的作用，橫向振動位移w可表示為

式中： 為滿足齊次邊界條件的解， 為不滿足齊次邊界的解。

2 系統離散化求解

采用Galerkin法將系統振動控制方程轉化為常微分方程，定義ξ=x/l(t)，將變量x的時變域[0，l(t)]歸一化為固定域[0，1]，設系統的振動控制方程解可表示為

式中：i=1、2、3、…、n，n為模態截斷階數；φi(ξ)為型函數；pi(t)和qi(t) 為只與時間相關的廣義坐標。

將式（13）代入式（11）和式（12）可得到激勵作用下系統的縱向-橫向振動偏微分方程。將式（13）按照振動控制方程中各項偏導數進行展開后代入式（10）和式（11），可將系統的橫向-縱向振動偏微分方程轉化為時變系數的常微分方程

式中：Pw和Qw為廣義坐標向量，Mu、Mw為系統的質量矩陣，Cu、Cw為系統的阻尼矩陣，Ku、Kw為系統的剛度矩陣，Fu、Fw為系統的廣義力向量，SPu、SPw為系統的耦合項。

各項表達式為

3 提升鋼絲繩振動響應仿真分析

高速曳引電梯作為典型的柔性提升系統，參數變化快，運行過程中提升鋼絲繩的長度不斷發生變化，系統的剛度、阻尼、質量的參數均會發生變化。以高速曳引電梯為例分析提升系統的橫向-縱向耦合振動特性。高速曳引電梯的最大行程lmax=175 m，額定速度vmax=6 m/s，最大加速度amax=0．75 m/s2，最大加加速度jmax=0．75 m/s3，運行時間為36 s。圖2為高速曳引電梯運行狀態曲線。高速曳引電梯中單根鋼絲繩的提升質量m=450 kg，鋼絲繩線密度ρ1=0.575 kg/m，抗彎剛度EI=22.16 N?m2，抗彎剛度ES=4.72 MN，導靴剛度k1=1×105N/m，阻尼c1=500 N?s/m，張緊繩線密度ρ2=0.490 kg/m，繩頭彈簧剛度k1=1×105 N/m，阻尼c1=50 N?s/m，張緊力F=500 N。根據GB/T 8903—2018《電梯用鋼絲繩》[20]，該規格的鋼絲繩最小破斷拉力Fmin=74.3 kN，安全系數應≥12。

圖2 高速曳引電梯運行狀態

張緊力F通過式（15）驗證，滿足國家標準。

以上述參數為輸入，使用Matlab軟件對系統振動控制方程進行分析，圖3和圖4分別為重物底部有平衡繩與無平衡繩的系統橫向振動位移響應與加速度響應。由于平衡繩的影響，上行時橫向振動位移響應幅值由0.536 mm降低至0.524 mm，加速度響應由0.22 m/s2減小至0.173 m/s2，下行時的振動位移響應幅值降低了0.12 mm，加速度響應僅降低0.008 m/s2。圖5和圖6為分別為2種情況的縱向振動，由于底部平衡繩的質量以及張緊力的關系，系統縱向受力變大，縱向振動加速度更為劇烈，振動加速度幅值達0.91 m/s2隨后在4 s內降低至0.5 m/s2，振動位移變化較小。提升系統底部安裝平衡繩可抑制系統的橫向振動，但會使系統的縱向振動更為劇烈。分析發現，系統上行時的振動響應幅值比下行時的振動響應幅值大，系統在下行時，系統的振動頻率與幅值不斷下降，上行時的振動頻率與幅值不斷增加。由于提升鋼絲繩的結構特點，鋼絲繩在系統停止運行后，存在少量的殘余振動，系統軸向的殘余振動更為明顯，由于平衡繩的影響，系統的縱向振動位移殘余響應由0.4 mm增加至3.85 mm。

圖3 無平衡繩的系統橫向振動位移與加速度響應

圖4 有平衡繩的系統橫向振動位移與加速度響應

圖5 無平衡繩的系統縱向振動位移與加速度響應

圖6 有平衡繩的系統縱向振動位移與加速度響應

4 導軌不平順振動響應分析

導軌作為提升系統的導向裝置，是不平順時系統振動的主要激勵源，導軌支架與連接板的安裝失誤將會導致導軌出現文獻[21]中描述的失調激勵ec(t)，如圖7所示，失調激勵的數學表達式為

圖7 失調激勵

式中：e為失調激勵幅值，ecmax=0.5 mm；h為單根導軌長度；n為導軌數量。

將導軌不平順激勵視為外力作用在系統導靴裝置上，將不平順激勵化為對導靴的力學參數。此時系統中阻尼做的虛功變為

同時，系統的張緊力變為

式中：μ為滑動摩擦系數。

將式（20）與式（21）代入式（6）和式（9），可得到系統在導軌不平順激勵下系統的振動控制方程。系統具體結構參數如文前所述，單根導軌長度為5 m，由系統的行程可知兩側均需采用36 根導軌。

圖8和圖9分別為導軌失調不平順激勵的系統位移與加速度響應。由圖4和圖8可知，在導軌不平順處系統的橫向振動位移較大且存在突變，振動位移響應突變幅值為5.1 mm，加速度響應較為劇烈，由圖6和圖9可知，導軌不平順對系統的縱向振動響應無影響。

圖8 失調激勵對系統橫向振動的影響

圖9 失調激勵對系統縱向振動的影響

5 結語

本文針對柔性提升系統軸向運動的時變特性考慮平衡鋼絲繩及其張緊力的影響，根據運動過程中提升鋼絲繩的非線性特征，基于Hamliton原理建立橫向-縱向耦合振動控制方程。以高速曳引電梯為例，將擬合的運行狀態參數作為振動方程的輸入條件，采用Matlab軟件對有無平衡繩的系統進行振動響應分析。結果表明：有平衡繩的系統橫向振動位移、加速度響應幅值均有明顯降低，其中系統上行時的橫向振動加速度響應降低20%，下行時降低5%。平衡繩及其張緊力會增加系統的縱向受力，導致系統的縱向振動位移、加速響應幅值較大，系統停止運行后的殘余振動響應為3.85 mm。導軌不平順會引起系統橫向振動出現突變，且系統在突變處的振動較為劇烈，振動幅值為5.1 mm；導軌不平順對系統的縱向振動影響較小，故在設計提升系統時應對運行導軌的不平順問題加以控制。上述研究結果可為電梯柔性提升系統及相似系統的振動控制與振動特性研究提供一定的參考。