平面圖形的靜矩與慣性矩關(guān)系系數(shù)研究

俞曉明 ，陳 蘭

1.鹽城工學(xué)院 數(shù)理學(xué)院，江蘇 鹽城 224002；2.鹽城市鹽都區(qū)教師發(fā)展中心，江蘇 鹽城 224005

液罐半掛車(chē)是液體危險(xiǎn)品道路運(yùn)輸?shù)闹饕ぞ摺．?dāng)罐車(chē)上下坡時(shí)，液體系統(tǒng)的質(zhì)心位置改變，導(dǎo)致汽車(chē)的軸荷分配等發(fā)生變化，從而對(duì)汽車(chē)的穩(wěn)定性產(chǎn)生不利影響［1］，導(dǎo)致汽車(chē)側(cè)傾事故的頻繁發(fā)生［2-5］。因此，研究罐車(chē)系統(tǒng)的穩(wěn)度具有重要的工程意義。

1 理論基礎(chǔ)

對(duì)于矩形和立式圓柱液罐系統(tǒng)，其液位的高度計(jì)算較為簡(jiǎn)易，而兩端為平蓋的圓柱形或橢圓形的臥式液罐系統(tǒng)，液位高度的計(jì)算就比較復(fù)雜［6-8］。本文主要研究斜立式圓柱罐體系統(tǒng)的穩(wěn)度問(wèn)題。

1.1 模型假設(shè)

為研究方便，作如下假設(shè)：（1）液罐為圓柱形剛性容器，忽略車(chē)體的質(zhì)量和尺寸，以及罐壁罐底的質(zhì)量和厚度；（2）液罐與坡面間的摩擦系數(shù)足夠大，以致汽車(chē)在坡面上行駛時(shí)液罐不下滑；（3）液面為水平，忽略液體表面張力引起罐內(nèi)液面的凹凸；（4）液體為靜態(tài)，忽略黏滯阻力以及振動(dòng)等；（5）罐壁足夠高，罐體處于臨界傾角時(shí)罐內(nèi)液體沒(méi)有溢出。

1.2 力矩分析

裝有一定量液體的圓柱形液罐靜置在坡面上，液體模型如圖1 所示、受力如圖2 所示。設(shè)圓柱形液罐的直徑為2R，坡面與水平面夾角為θ，液體的密度為ρ，重力加速度為g，液體與罐底面的交線MN 為y 軸，MN 的中點(diǎn)O 為坐標(biāo)系原點(diǎn)，x 軸沿直徑QP 方向，z 軸垂直于罐底面向上，如圖1b所示。

圖1 坡面上圓柱形罐內(nèi)的液體模型Fig. 1 Model of liquid body in cylindrical oil tan on inclined plane

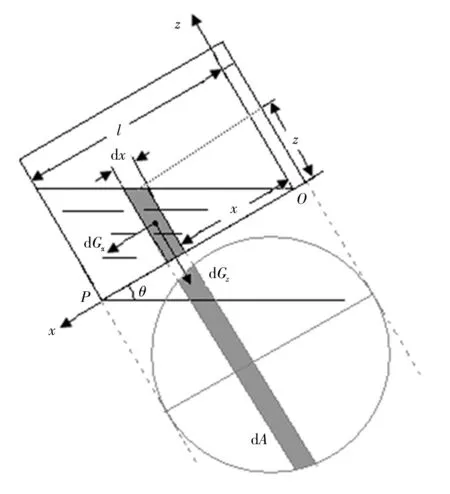
圖2 坡面上圓柱形罐內(nèi)液體的受力示意圖Fig. 2 Stress diagram of liquid body in cylindrical oil tan on inclined plane

在xOy 平面內(nèi)的x軸上距原點(diǎn)x處取寬度d x、高度z=x tan θ 的板形液體微元，其面積為d A、體積d V=x tan θd A、重力d G=ρgx tan θd A，則d G 的分量這兩分量對(duì)過(guò)點(diǎn)P 且平行于y 軸的力矩分別為d MPy(d Gx)=則整個(gè)重力的分力矩及液體體積分別為：

式中：l為液體在罐底面上的投影在x軸上的長(zhǎng)度，m；JOy=x2dA，為該投影對(duì)y軸的慣性矩，m4；SOy=xdA，為該投影對(duì)y軸的靜矩，m3。

式（3）表明：圓柱形液罐內(nèi)液體體積V等于液體在罐底面上投影的靜矩Soy與坡面傾角正切值tanθ的乘積。

1.3 臨界傾角確定

液罐不發(fā)生傾倒的條件為：

2 平面圖形靜矩與慣性矩關(guān)系系數(shù)

2.1 關(guān)系系數(shù)的定義

對(duì)于xOy平面內(nèi)的圖形K（圖3），在K上任一點(diǎn)（x′，y′）處取面元dA，則K繞y軸、x軸的靜矩和慣性矩分別為：

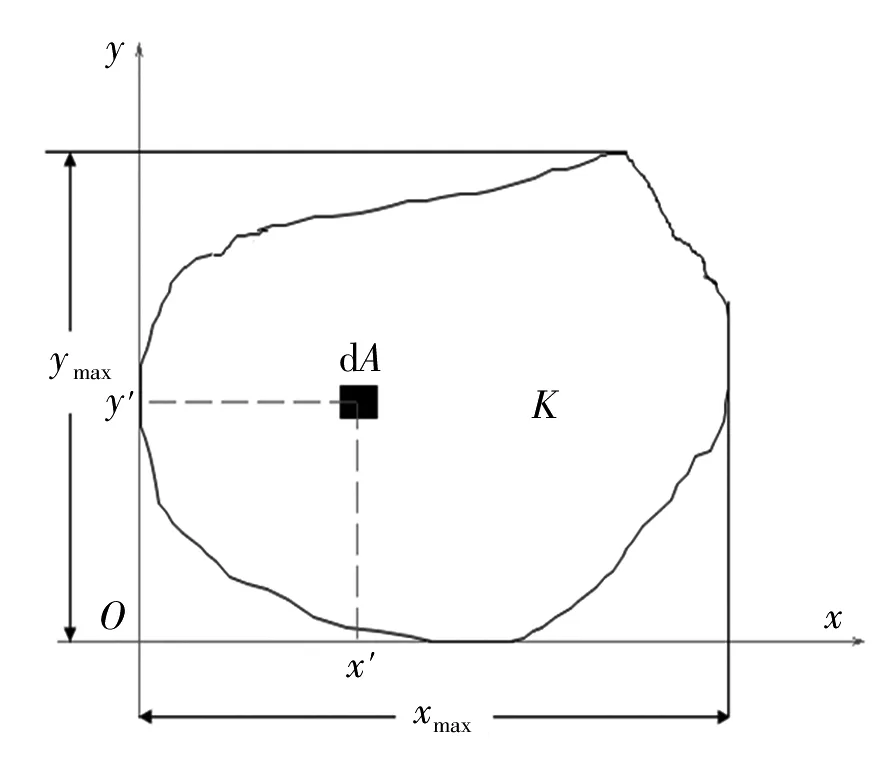
圖3 平面圖形KFig. 3 plane graph K

定義平面圖形K繞y軸、x軸的靜矩與慣性矩關(guān)系系數(shù)分別為：

式中：xmax、ymax分別為平面圖形K在x、y軸上的特征長(zhǎng)度，m。對(duì)于平面圖形，如圓盤(pán)的直徑、橢圓的軸長(zhǎng)、矩形的邊長(zhǎng)以及等邊三角形的邊長(zhǎng)等均為各自的特征長(zhǎng)度。

根據(jù)靜矩與慣性矩關(guān)系系數(shù)，式（5）可改寫(xiě)成：

式（11）表明，坡面上罐體的臨界傾角取決于罐內(nèi)液體在罐底面上投影的靜矩與慣性矩關(guān)系系數(shù)。因此，研究罐體的臨界傾角就轉(zhuǎn)化為研究投影的靜矩與慣性矩關(guān)系系數(shù)的問(wèn)題。

罐體的形態(tài)不同，則投影平面的形狀不同，靜矩與慣性矩關(guān)系系數(shù)也不相同，因此，尋求不同平面圖形的靜矩與慣性矩關(guān)系系數(shù)是解決液體系統(tǒng)穩(wěn)度問(wèn)題的重要課題，但本文重點(diǎn)探尋平面圖形靜矩與慣性矩關(guān)系系數(shù)具有的基本性質(zhì)，這對(duì)解決一般液體系統(tǒng)的穩(wěn)度問(wèn)題具有普適意義。

2.2 關(guān)系系數(shù)的性質(zhì)

2.2.1 標(biāo)度變換不變性

對(duì)于由單調(diào)連續(xù)函數(shù)y1=f1（x）、y軸、x1=a和x軸圍成平面圖形M1（圖4），它的x軸特征長(zhǎng)度為xmax1=a，其面積和繞y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

圖4 中，先固定M1在x軸上的邊，將M1沿y軸放大k1倍（k1>0）；再固定M1在y軸上的邊，將圖形沿x軸放大k2倍（k2>0），得到平面圖形M2。此時(shí)M2由函數(shù)y2=f2（x）、y軸、x2=k2a和x軸圍成，它的x軸特征長(zhǎng)度為xmax2=k2xmax1=k2a，其面積和繞y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

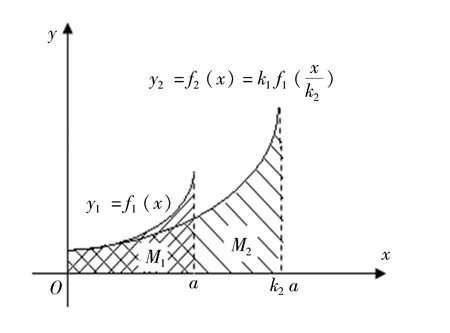
圖4 標(biāo)度變換不變性推證用圖Fig. 4 Diagram for proof that has invariance of scale transformation

分別比較式（12）與式（16）、式（13）與式（17）、式（14）與式（18）、式（15）與式（19），可知：平面圖形先后沿y軸、x軸放大k1、k2倍后，其面積變?yōu)樵瓉?lái)的k1k2倍，繞y軸的靜矩變?yōu)樵瓉?lái)的倍、慣性矩變?yōu)樵瓉?lái)的k1k32倍，而靜矩與慣性矩關(guān)系系數(shù)保持不變。

同理可證，平面圖形放大后，繞x軸的靜矩與慣性矩關(guān)系系數(shù)也保持不變，即px2=px1。

物體尺度大小的變換叫做“標(biāo)度變換”，標(biāo)度變換過(guò)程中平面圖形的靜矩與慣性矩關(guān)系系數(shù)保持不變的性質(zhì)，稱(chēng)為平面圖形靜矩與慣性矩關(guān)系系數(shù)的標(biāo)度變換不變性。平面圖形靜矩與慣性矩關(guān)系系數(shù)的標(biāo)度變換不變性為工程試驗(yàn)的小規(guī)模化提供了理論依據(jù)。利用該理論可以在實(shí)踐中將大尺度液體系統(tǒng)的穩(wěn)度問(wèn)題通過(guò)縮小系統(tǒng)尺寸轉(zhuǎn)換為小尺度問(wèn)題進(jìn)行研究。

2.2.2 定軸平移不變性

平面圖形N1處于xOy平面內(nèi)（圖5），在N1上（xi，yi）處取面元dAi，則N1繞y軸的靜矩與慣性矩關(guān)系系數(shù)為：

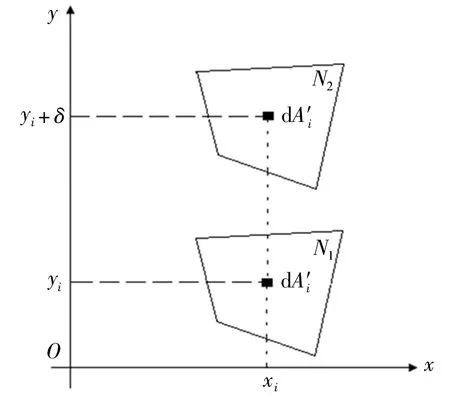
圖5 定軸平移不變性推證用圖Fig. 5 Diagram for proof that has invariance of translation along fixed axis

將N1沿y軸平移δ得到N2，在N2上（xi，yi+δ）處取與dAi相同的面元dAi′，則N2繞y軸的靜矩與慣性矩關(guān)系系數(shù)為：

若將N1沿x軸平移任意距離，同理可證px2=px1。

式（21）表明：平面圖形在其平面內(nèi)沿定軸平移時(shí)，繞定軸的靜矩與慣性矩關(guān)系系數(shù)保持不變。該結(jié)論稱(chēng)為平面圖形靜矩與慣性矩關(guān)系系數(shù)的定軸平移不變性。

2.2.3 第一類(lèi)平面圖形的垂直軸等值性

設(shè)平面圖形T在第一象限內(nèi)由函數(shù)y=f（x）和它的反函數(shù)x=f-1（y）組成（圖6），由于函數(shù)和它的反函數(shù)關(guān)于y=x對(duì)稱(chēng)，從而軸y=x將T分成兩個(gè)對(duì)稱(chēng)區(qū)域A1、A2。在A1內(nèi)（xi，yi）處取面元dAi，在A2內(nèi)取dAi關(guān)于y=x對(duì)稱(chēng)的面元dAi′，根據(jù)對(duì)稱(chēng)性有xi=y′i，從而xidAi=y′idA′i，x2idAi=y′i2dA′i。

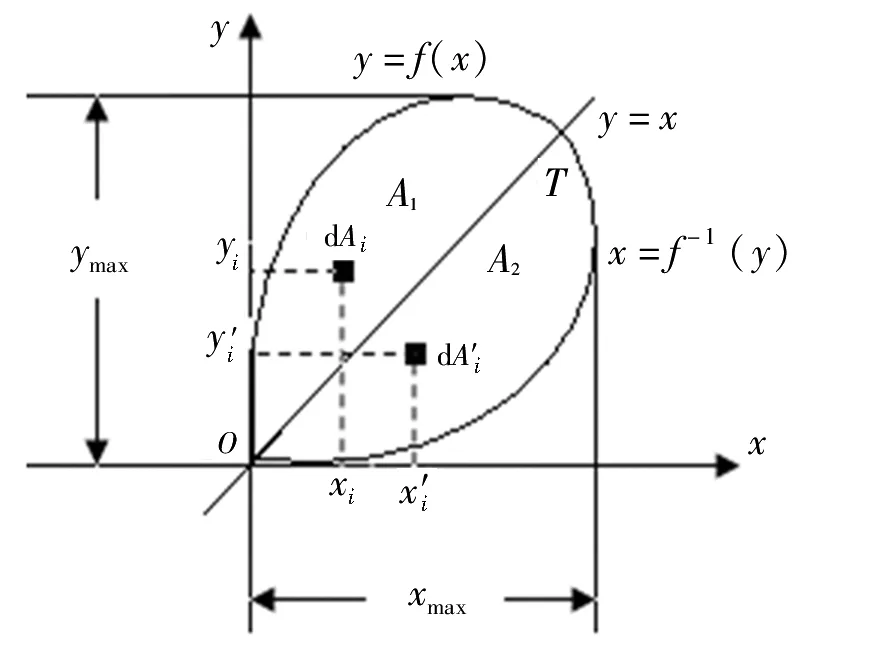
圖6 垂直軸等值性推證用圖Fig. 6 Diagram for proof that has equivalence on plane graph

在A1區(qū)域，有

從而得到平面圖形T對(duì)坐標(biāo)軸的靜矩、慣性矩關(guān)系，如下所示：

設(shè)平面圖形T在x、y軸的特征長(zhǎng)度分別為xmax、ymax，因?yàn)門(mén)關(guān)于軸y=x對(duì)稱(chēng)，有ymax=xmax。此時(shí)T對(duì)坐標(biāo)軸的靜矩與慣性矩關(guān)系系數(shù)滿足：

式（22）表明：關(guān)于軸y=x對(duì)稱(chēng)的平面圖形，繞相互垂直軸的靜矩與慣性矩關(guān)系系數(shù)相等。這類(lèi)特殊的平面圖形稱(chēng)為第一類(lèi)平面圖形，該結(jié)論為平面圖形靜矩與慣性矩關(guān)系系數(shù)的垂直軸等值性。

進(jìn)一步研究表明，還存在第二類(lèi)平面圖形，它們雖然并不關(guān)于軸y=x對(duì)稱(chēng)，但繞相互垂直軸的靜矩與慣性矩關(guān)系系數(shù)也相等，這將另文闡述。

3 有質(zhì)平面圖形靜矩與慣性矩關(guān)系系數(shù)

3.1 關(guān)系系數(shù)的定義

目前，研究平面圖形靜矩與慣性矩關(guān)系系數(shù)時(shí)并未考慮質(zhì)量，而質(zhì)量是決定液體系統(tǒng)穩(wěn)度的重要因素。因此，從理論上探索有質(zhì)物體穩(wěn)度的計(jì)算方法，對(duì)解決實(shí)際工程問(wèn)題具有重要指導(dǎo)價(jià)值。

為敘述方便，本文將考慮質(zhì)量的平面圖形稱(chēng)為有質(zhì)平面圖形，質(zhì)量在平面內(nèi)的分布狀態(tài)用質(zhì)量面密度描述。

設(shè)有質(zhì)平面圖形U處于xOy平面內(nèi)（圖7），在U上（x0，y0）處取面元dA，dA的質(zhì)量面密度為σ（x0，y0），則U繞y軸的靜矩、慣性矩（此時(shí)也稱(chēng)轉(zhuǎn)動(dòng)慣量）以及繞x軸的靜矩、慣性矩分別為：

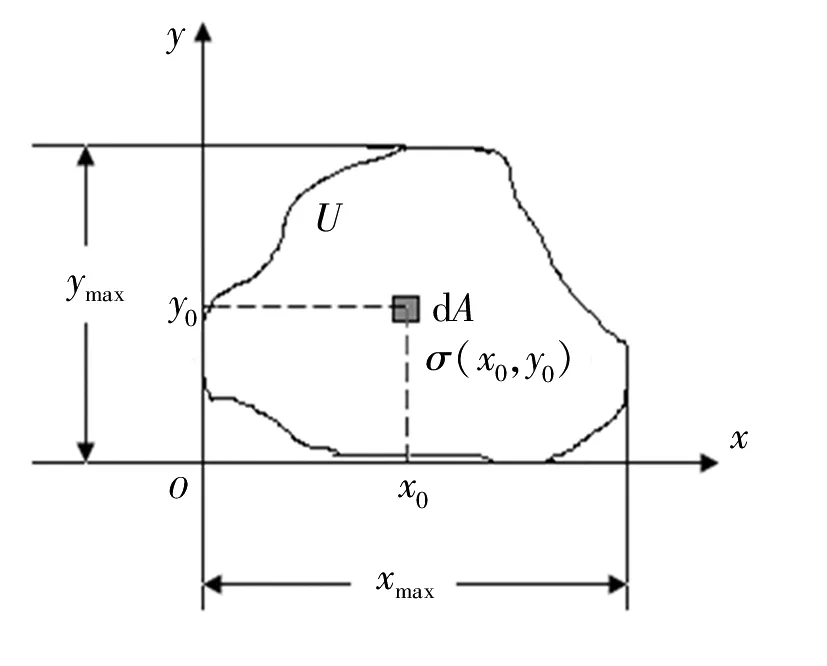
圖7 有質(zhì)平面圖形靜矩與慣性矩關(guān)系系數(shù)的定義用圖Fig. 7 Diagram for definition of relation coefficient between static moment and moment of inertia with mass on plane graph

定義有質(zhì)平面圖形U繞y軸、x軸的靜矩與慣性矩關(guān)系系數(shù)分別為：

式中：x′max、y′max分別為平面圖形U在x、y軸上的特征長(zhǎng)度，m。

3.2 標(biāo)度變換時(shí)有質(zhì)平面圖形的靜矩與慣性矩關(guān)系系數(shù)

3.2.1 軸向冪函數(shù)分布狀態(tài)下的靜矩與慣性矩關(guān)系系數(shù)

在xOy平面內(nèi)由單調(diào)連續(xù)函數(shù)y1=f1（x）、x軸、y軸和x=a圍成的有質(zhì)平面圖形V1（圖8），其質(zhì)量面密度沿x軸方向按冪函數(shù)σ（x）=λxn（λ為常量，且λ≠0）分布，而y軸方向不變，則V1對(duì)y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

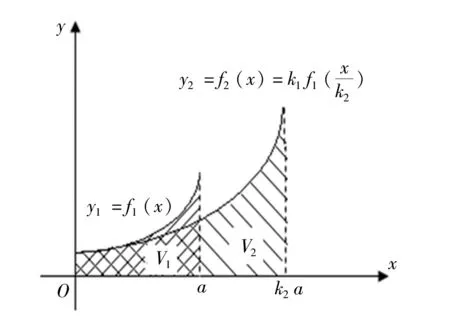
圖8 面密度呈冪函數(shù)分布的有質(zhì)平面圖形標(biāo)度變換不變性推證用圖Fig. 8 A proof diagram for scale transformation invariance of qualitative plane figure with power function distribution of areal density

圖8 中，先固定V1在x軸上的邊，將V1沿y軸標(biāo)度變換k1倍；再固定V1在y軸上的邊，將圖形沿x軸標(biāo)度變換k2倍，得到V2，則V2在x軸的特征長(zhǎng)度xmax2=k2xmax1=k2a，V2對(duì)y軸的靜矩、慣性矩及靜矩與慣性矩關(guān)系系數(shù)分別為：

分別比較式（28）與（31）、式（29）與（32）、式（30）與（33），可知：質(zhì)量面密度沿x軸按冪函數(shù)σ（x）=λxn（λ為常量，且λ≠0）分布，而y軸方向不變時(shí)，有質(zhì)平面圖形沿y軸標(biāo)度變換k1倍、再沿x軸標(biāo)度變換k2倍后，其靜矩變?yōu)樵瓉?lái)的k1kn+22倍、慣性矩變?yōu)樵瓉?lái)的k1kn+32倍，而靜矩與慣性矩關(guān)系系數(shù)保持不變。

分別比較式（13）～式（15）與式（28）～式（30）、式（17）～式（19）與式（31）～式（33），可知：（1）平面圖形因考慮了質(zhì)量，其靜矩、慣性矩以及繞坐標(biāo)軸的靜矩與慣性矩關(guān)系系數(shù)一般都會(huì)發(fā)生變化；（2）盡管標(biāo)度變換過(guò)程中有質(zhì)平面圖形的靜矩與慣性矩關(guān)系系數(shù)保持不變，但該系數(shù)與不考慮質(zhì)量時(shí)的值一般不同。

考慮特殊情形，若令n=0（x≠0），則σ（x）=λ，即質(zhì)量面密度沿x軸為常值λ，此時(shí)平面圖形V1對(duì)y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

標(biāo)度變換后平面圖形V2對(duì)y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

分別比較式（13）與（34）、式（17）與（37）以及式（14）與（35）、式（18）與（38），可知：質(zhì)量面密度沿x軸（x≠0）為常數(shù)λ而y軸方向不變時(shí)，有質(zhì)平面圖形的靜矩和慣性矩總是不考慮質(zhì)量時(shí)的λ倍，與是否進(jìn)行標(biāo)度變換及變換比例無(wú)關(guān)。這說(shuō)明質(zhì)量分布對(duì)平面圖形的靜矩和慣性矩有著重要影響。

比較式（13）與（17）、式（34）與（37）以及式（14）與（18）、式（35）與（38），可知：質(zhì)量面密度沿x軸（x

≠ 0）為常數(shù)λ，而y軸方向不變時(shí)，將圖形沿y軸標(biāo)度變換k1倍、再沿x軸標(biāo)度變換k2倍后，其靜矩變?yōu)樵瓉?lái)的倍、慣性矩變?yōu)樵瓉?lái)的倍。這說(shuō)明標(biāo)度變換過(guò)程中有質(zhì)平面圖形靜矩和慣性矩的變化比例與質(zhì)量面密度λ無(wú)關(guān)，但受制于變換比例k1、k2。

比較式（30）與式（33）、式（36）與式（39），可知：質(zhì)量面密度相等時(shí)，有質(zhì)平面圖形的靜矩與慣性矩關(guān)系系數(shù)在標(biāo)度變換過(guò)程中始終保持不變，與是否考慮質(zhì)量無(wú)關(guān)。

3.2.2 質(zhì)量保持不變時(shí)的靜矩與慣性矩關(guān)系系數(shù)

在xOy平面內(nèi)由單調(diào)連續(xù)函數(shù)y1=f1（x）、x軸和x=a、y軸圍成的有質(zhì)平面圖形W1（圖9），其質(zhì)量面密度均勻分布且為σ1，則平面圖形W1的面積和繞y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

圖9 中，將W1沿y軸標(biāo)度變換k1倍，再沿x軸標(biāo)度變換k2倍后，得到W2，則W2的面積為：

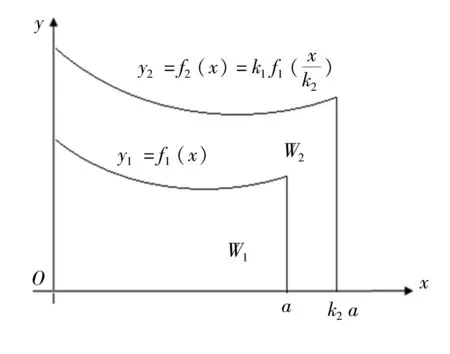
圖9 質(zhì)量保持不變的有質(zhì)平面圖形標(biāo)度變換不變性推證用圖Fig. 9 A proof diagram for scale transformation invariance of qualitative plane figure with constant quality

設(shè)W2的質(zhì)量面密度也均勻，且為σ2，由于標(biāo)度變換過(guò)程中質(zhì)量保持不變，即質(zhì)量m=σ1A1=σ2A2，所以σ1與σ2間存在如下關(guān)系。

W2對(duì)y軸的靜矩、慣性矩以及靜矩與慣性矩關(guān)系系數(shù)分別為：

式（41）～式（48）表明：在質(zhì)量保持不變時(shí)，有質(zhì)平面圖形沿y軸標(biāo)度變換k1倍、再沿x軸標(biāo)度變換k2倍后，其質(zhì)量面密度會(huì)發(fā)生變化，繞y軸的靜矩、慣性矩也會(huì)變化，但靜矩與慣性矩關(guān)系系數(shù)保持不變，并且與不考慮質(zhì)量時(shí)相同。

以上研究表明：對(duì)于有質(zhì)平面圖形，只要質(zhì)量面密度處處相等，無(wú)論是否進(jìn)行標(biāo)度變換，它的靜矩與慣性矩關(guān)系系數(shù)總保持不變，且與不考慮質(zhì)量時(shí)相同。

4 結(jié)語(yǔ)

本文在模型假設(shè)的基礎(chǔ)上推導(dǎo)出罐體臨界傾角的表達(dá)式，將液體系統(tǒng)穩(wěn)度的立體問(wèn)題轉(zhuǎn)化為平面問(wèn)題，進(jìn)而轉(zhuǎn)化為平面圖形的靜矩與慣性矩關(guān)系系數(shù)的問(wèn)題。研究發(fā)現(xiàn)，對(duì)于平面圖形，只要質(zhì)量面密度處處相等，無(wú)論是否進(jìn)行標(biāo)度變換，它的靜矩與慣性矩關(guān)系系數(shù)總保持不變，且與不考慮質(zhì)量時(shí)相同。該結(jié)論對(duì)于研究工程中液體系統(tǒng)的穩(wěn)度問(wèn)題具有理論指導(dǎo)意義。