非均勻風下流線型箱梁懸索橋靜風穩定性分析

單秋偉 張亮亮 言志超 楊建新

摘 要：大跨度懸索橋結構輕柔，風致響應明顯。借助有限元方法，考慮懸索橋的幾何非線性和位移荷載非線性，對非均風攻角來流沿主梁對稱分布和非對稱分布以及非均勻風速來流沿主梁對稱分布和非對稱分布時懸索橋的非線性靜風穩定性展開研究。結果表明：正攻角來流會降低橋梁的靜風失穩臨界風速，負攻角來流有利于橋梁抵抗靜風失穩，且負攻角來流對橋梁的靜風穩定性影響程度比正攻角來流影響程度大;非均勻風攻角來流非對稱分布時，可由小風攻角來流確定的靜風失穩臨界風速作為穩定性判斷依據，非均勻風攻角來流對稱分布時，可以選擇平均攻角來流衡量橋梁的靜風穩定性。非均勻風速來流對橋梁的靜風穩定性有不利影響，且非均勻風速來流對稱分布時的影響比非均勻風速來流非對稱分布時的影響更大。在不同初始攻角下，這類來流對橋梁靜風穩定性有著相似的影響，橋梁的靜風失穩臨界風速均隨著風速非均勻程度增大而減小。

關鍵詞：懸索橋;流線型箱梁;非線性;靜風穩定性;非均勻風

中圖分類號：U448.25 ? 文獻標志碼：A ? 文章編號：2096-6717（2022）01-0117-09

收稿日期：2020-07-08

基金項目：重慶市教委科學技術研究項目（KJZD-k201802501）;重慶市技術創新與應用示范（社會民生類）一般項目（cstc2018jscx-msybX0277）

作者簡介：單秋偉（1994- ），男，主要從事大跨度橋梁抗風研究，E-mail：shanqiuwei@foxmail.com。

張亮亮（通信作者），男，教授，博士生導師，E-mail：zll200510@126.com。

Abstract： The long-span suspension bridges， which are notable flexibility， are sensitive to wind load. Using the finite element method， considering the geometric nonlinearity and displacement-load nonlinearity， the aerostatic stability of suspension bridges is studied when the non-uniform wind attack angle flow and non-uniform wind speed flow distributes symmetrically and asymmetrically along the main girder. The results show that the flow of positive angle of attack will reduce the critical stability wind speed of the bridges， the flow of negative angle of attack is conducive to the bridges to resist the instability of static wind. The impact of negative angle of attack on the static wind stability of the bridge is greater than that of positive angle of attack. When the flow is asymmetrically distributed， the critical stability wind speed can be determined by small wind angle of attack. When the flow is symmetrically distributed， the mean angle of attack can be selected to measure the aerostatic stability of the bridge. Incoming flow with non-uniform wind speed has an adverse effect on the aerostatic stability of the bridge. Moreover， the influence of symmetric distribution of non-uniform wind speed is greater than that of asymmetric distribution of non-uniform wind speed.Under different initial angles of attack， this kind of incoming flow has similar effects on the static wind stability of the bridge. That's to say， the critical wind speed of aerostatic stability of the bridge decreases with the increase of the unevenness of the wind speed.

Keywords： suspension bridge; streamlined box girder; nonlinearity; aerostatic stability; non-uniform wind

隨著橋梁建設能力的提升，橋梁跨徑越來越大，但跨徑的增大往往會使橋梁趨于輕柔，進而降低橋梁的穩定性。橋梁在建造和使用過程中一般需要考慮風災、撞擊和震害等影響，其中，風災對橋梁結構的影響最為劇烈，發生頻率也最高，由此造成的社會經濟損失最為嚴重[1]。因此，在修建大跨度橋梁時，必須要考慮到橋梁結構對風作用的響應，并采取相應的措施降低其對結構的影響。

許多學者對大跨度橋梁的靜風穩定性開展了研究。Boonyapinyo等[2]采用有限元方法，考慮橋梁幾何非線性以及位移相關風荷載非線性，對大跨度斜拉橋在風荷載作用下的彎扭屈曲失穩臨界風速進行了計算。程進等[3]采用非線性方法開展了江陰長江大橋的參數分析和比較，發現懸索橋的靜風穩定性隨著初始攻角的增大而降低。Cheng等[4-6]提出了大跨度斜拉橋和懸索橋靜風穩定性的非線性方法，并開發了相應的分析程序。Boonyapinyo等[7]提出了一種考慮位移非線性、幾何非線性和材料非線性的大跨度懸索橋靜風穩定性的非線性分析方法，并分析了影響大跨度懸索橋靜風穩定性的因素。李永樂等[8]采用風荷載增量和雙重迭代相結合的方法對大跨度懸索橋的靜風失穩形態以及機理進行了研究。Xu等[9]研究了斜拉橋的非線性靜風穩定性，發現初始風攻角對橋梁靜風穩定性影響極大。管青海等[10-11]分析了大跨度懸索橋的靜風失穩發展過程以及影響因素。張文明等[12-13]研究了平均風速空間分布下懸索橋的靜風穩定性，結果表明，風速空間分布對懸索橋靜風穩定性的影響不可忽略。Zhou等[14]研究了雙主跨懸索橋的靜風失穩模式和破壞機理，發現此類懸索橋存在兩種失穩模式。張玉琢等[15]在進行靜風穩定性分析時發現非線性效應對靜風穩定性的影響不可忽視。Dong等[16]基于逆可靠度評估法分析了大跨度斜拉橋的靜風穩定性安全系數。胡朋等[17-18]對山區峽谷非均勻風場下大跨度斜拉橋的靜風穩定性進行了分析，結果表明，非均勻風攻角下大橋的靜風失穩臨界風速遠遠低于均勻風攻角下的靜風失穩臨界風速。

上述研究多集中在空間均勻風下的靜風穩定性，對非均勻風下的靜風穩定性研究較少，因此，有必要對大跨度懸索橋在非均勻風下的靜風穩定性開展研究，從而保證大跨度懸索橋在建設和運營狀態下的安全。筆者利用有限元分析軟件ANSYS的APDL語言，采用非線性分析方法，對非均勻風攻角和非均勻風速下大跨度懸索橋的靜風穩定性進行分析。

1 靜風穩定性分析理論

1.1 風的靜力作用

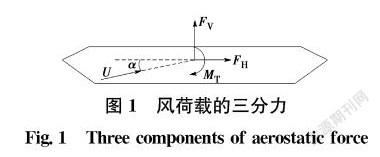
平均風作用會使處在風場中的結構產生一定的變形，風的作用相當于一個靜荷載[1]。將此荷載沿橋梁主梁斷面分解為阻力、升力和升力矩，稱為風荷載的三分力，如圖1所示。

借助ANSYS對大跨度懸索橋進行非線性靜風穩定性分析的具體過程：

1）給出初始風攻角α0和初始風速U0以及風速步長ΔU;

2）根據此時的風攻角和風速，計算主梁受到風荷載的三分力;

3）在ANSYS的靜態分析中，采用完全Newton-Rapson法求解式（5），得出模型主梁的位移，并從中提取出主梁各單元的扭轉角，重新計算主梁受到風荷載的三分力;

4）計算三分力系數的歐幾里得范數，當范數大于給定值時，重復執行過程3），使主梁達到該風速下的平衡狀態，若范數小于給定值，則增加一級風速，重復執行過程2）和3）;

5）若在計算過程中，出現了迭代不收斂，則將風速調整到上一次迭代狀態，減小風速步長，再進行計算，相鄰兩次迭代風速差值滿足要求時便可終止計算，相對應的最后一級風速即是失穩臨界風速。

2 大跨度懸索橋有限元模型

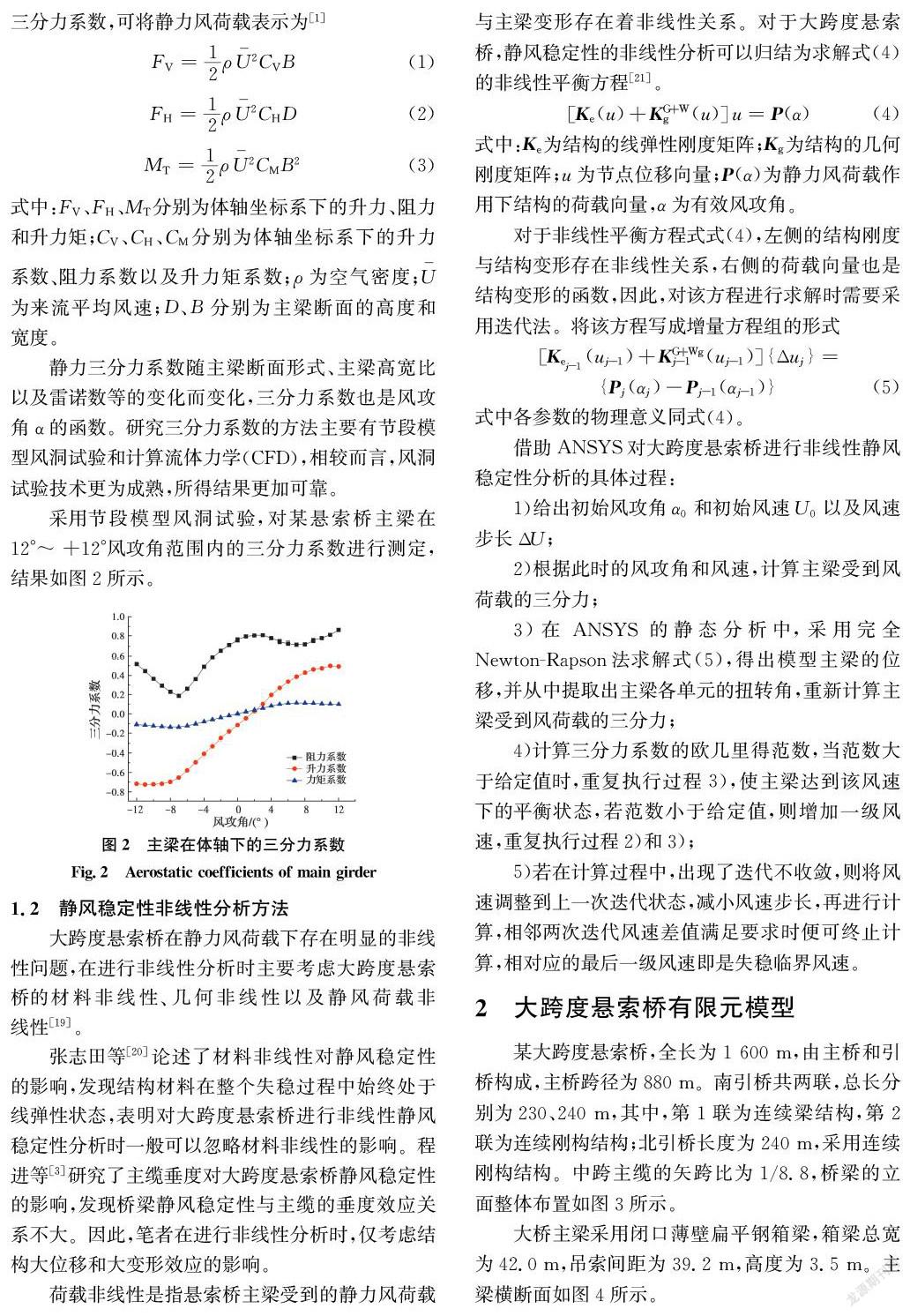
某大跨度懸索橋，全長為1 600 m，由主橋和引橋構成，主橋跨徑為880 m。南引橋共兩聯，總長分別為230、240 m，其中，第1聯為連續梁結構，第2聯為連續剛構結構;北引橋長度為240 m，采用連續剛構結構。中跨主纜的矢跨比為1/8.8，橋梁的立面整體布置如圖3所示。

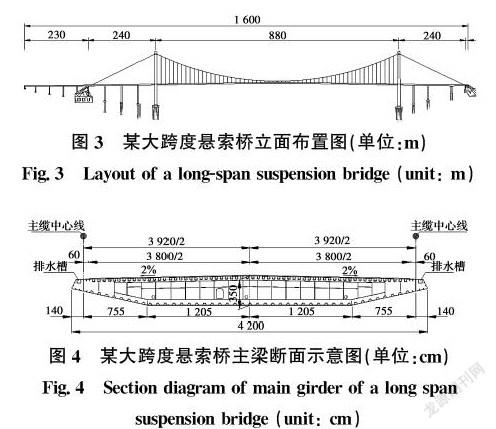
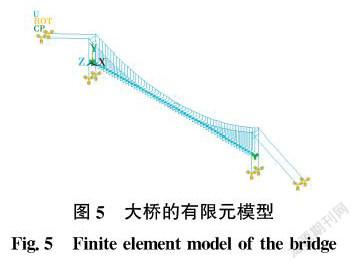
在ANSYS中，采用單主梁模型模擬主梁，單元類型選用beam4;主塔因其為變截面，故采用3D漸變梁單元beam44模擬;采用link10桿單元模擬主纜和吊索;mass21質量單元模擬主梁的質量慣矩和二期恒載。

大橋的邊界條件設置為：主塔底部固結，主纜錨固處固結，橋塔下橫梁與主梁采用耦合自由度方式進行連接，主塔下橫梁處設置combin14彈簧單元模擬縱向阻尼器，以限制主梁縱向位移。

全橋有限元模型共計705個節點，887個單元，如圖5所示。

3 非均勻風攻角下的靜風穩定性

自然界中的風場都是非均勻的，而前人的研究多以均勻流場為基礎，這樣的研究結果與真實情況可能存在偏差，因此，有必要開展非均勻風場下懸索橋的靜風穩定性分析。

為了研究非均勻風場中的非均勻風攻角風場對流線型箱梁懸索橋靜風穩定性的影響，根據風攻角分布區間的不同，設置了如圖6所示的兩類風攻角分布工況。

工況1考慮風攻角沿著橋跨方向非對稱分布的情況，主梁右半跨來流風攻角為α1，左半跨來流風攻角為α2。工況2則考慮風攻角沿著橋跨方向對稱分布的情況，主梁跨中1/2跨度范圍來流風攻角為α1，主梁兩端各1/4跨度范圍來流風攻角為α2。

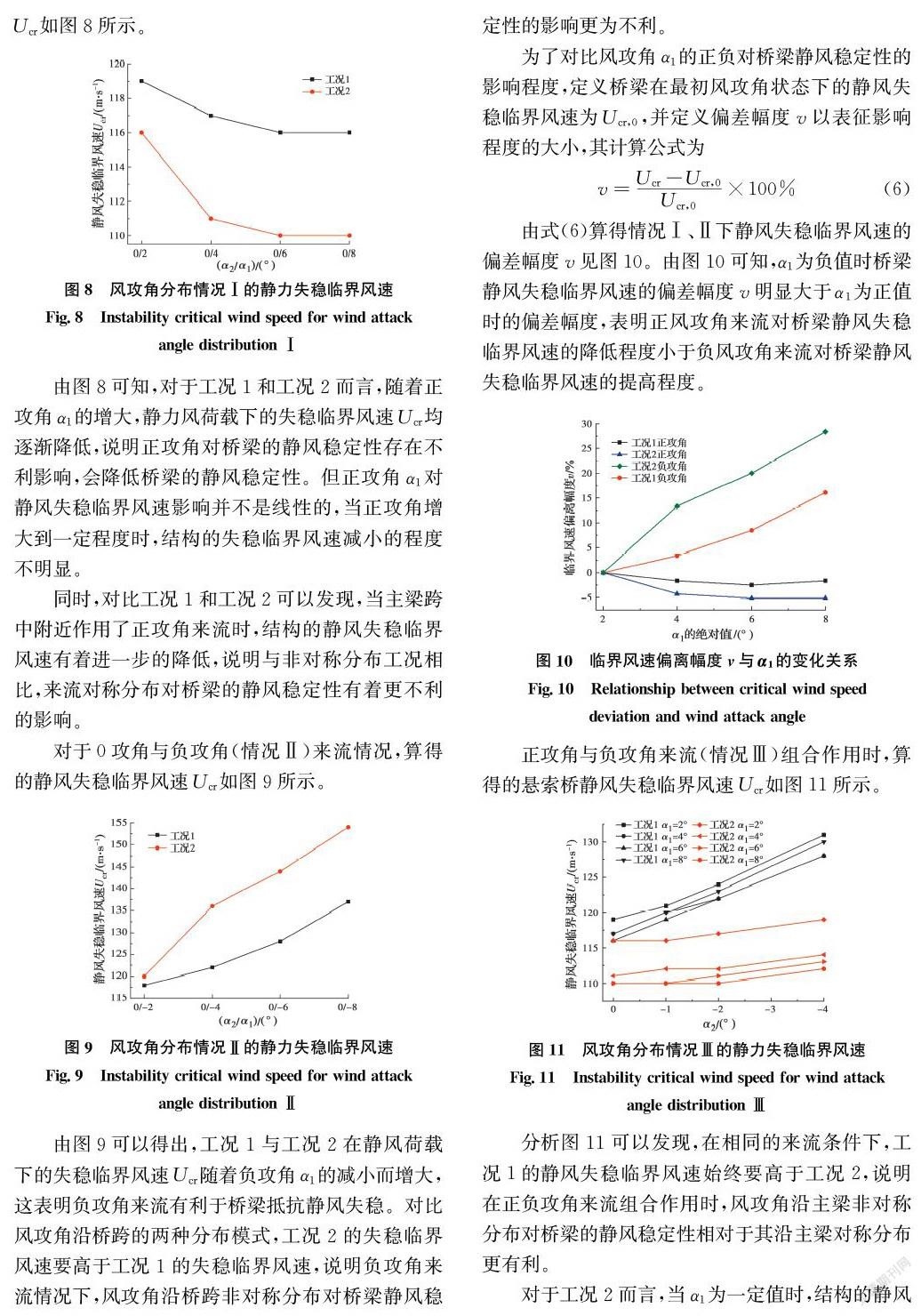
由圖12（a）可知，上述4種衡量方式所對應的偏離幅度a、b、c、d中，衡量方式Ⅱ的偏離幅度b最接近0，方式Ⅰ的偏離程度a最大，說明此衡量方式偏離實際情況的程度最嚴重，方式Ⅲ的偏離幅度c和方式Ⅳ的偏離幅度d也較大。說明對非對稱風攻角工況采用較小風攻角計算的靜風失穩臨界風速最接近實際情況，因此，可以采用小風攻角對非均勻風攻角來流進行靜風穩定性分析。但需要注意的是，當半跨來流風攻角接近于0°，另半跨來流負風攻角較大時，方式Ⅱ的偏離幅度較大，說明偏離程度較遠，此時，需要按照方式Ⅲ或方式Ⅳ來衡量靜風穩定性。

由圖12（b）可知，工況2下衡量方式Ⅳ的偏離幅度d在整體范圍內最接近0，表明對于風攻角對稱分布工況，可以采用大小風攻角的平均值進行非均勻風攻角來流下橋梁靜風穩定性的分析。但當主梁端部攻角接近于0°，跨中附近負攻角較大時，方式Ⅳ的偏離幅度較大，此時，應該采用小風攻角進行靜風穩定性分析。

4 非均勻風速下靜風穩定性

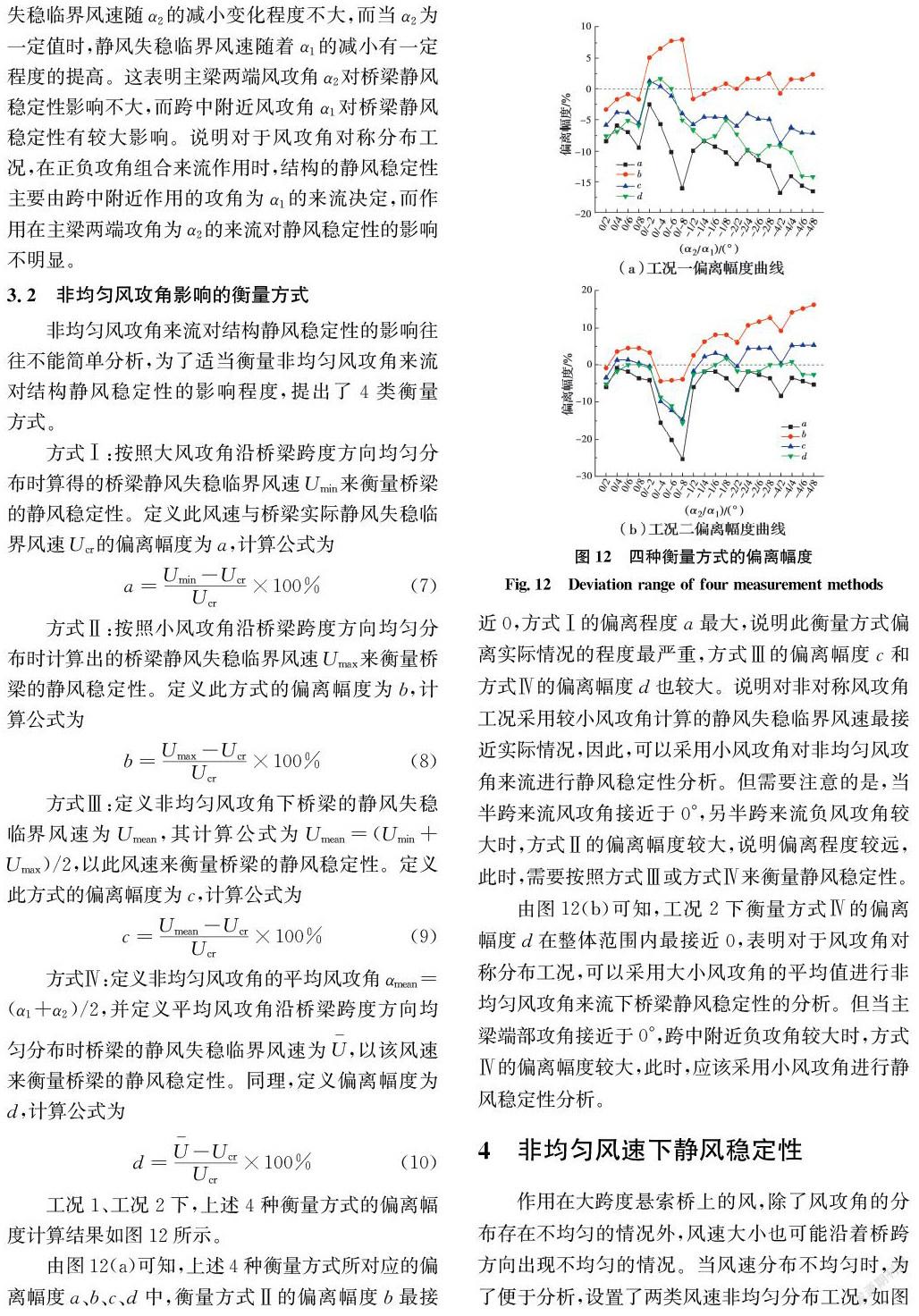
作用在大跨度懸索橋上的風，除了風攻角的分布存在不均勻的情況外，風速大小也可能沿著橋跨方向出現不均勻的情況。當風速分布不均勻時，為了便于分析，設置了兩類風速非均勻分布工況，如圖13所示。

參考明渠流流層流速分布規律，采用指數規律來描述主梁上的風速變化。工況1考慮風速沿主梁非對稱分布情況：主梁一端風速為U1，另一端風速為U2，主梁上的風速由U1到U2呈指數律變化。工況2考慮風速沿主梁對稱分布情況：主梁端部風速為U1，跨中風速為U2，端部到跨中的風速由U1到U2呈指數律變化。

為了分析風速的非均勻程度對大跨度懸索橋靜風穩定性的影響，設置了如表2所示的風速比值關系。

4.1 非均勻風速下靜風失穩臨界風速

非均勻分布風速下大橋靜風穩定性的比較須在同一基準下進行。以主梁全長范圍內非均勻分布風速下單位時間內總流量與均勻分布風速下單位時間內總流量相等為原則，在主梁全長范圍內對風速積分后取平均值作為平均靜風失穩臨界風速Ucr，即式

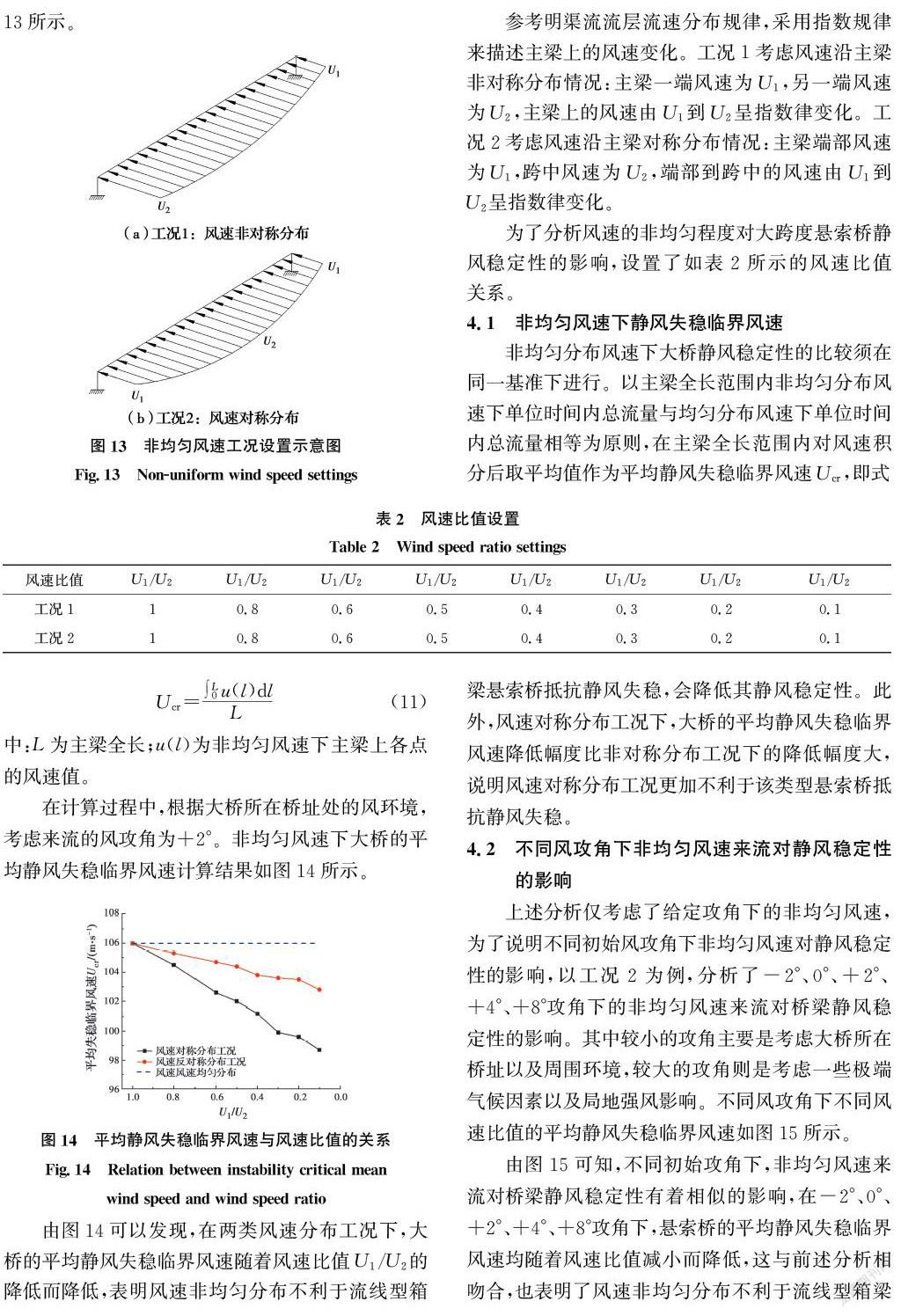
由圖14可以發現，在兩類風速分布工況下，大橋的平均靜風失穩臨界風速隨著風速比值U1/U2的降低而降低，表明風速非均勻分布不利于流線型箱梁懸索橋抵抗靜風失穩，會降低其靜風穩定性。此外，風速對稱分布工況下，大橋的平均靜風失穩臨界風速降低幅度比非對稱分布工況下的降低幅度大，說明風速對稱分布工況更加不利于該類型懸索橋抵抗靜風失穩。

4.2 不同風攻角下非均勻風速來流對靜風穩定性的影響

上述分析僅考慮了給定攻角下的非均勻風速，為了說明不同初始風攻角下非均勻風速對靜風穩定性的影響，以工況2為例，分析了-2°、0°、+2°、+4°、+8°攻角下的非均勻風速來流對橋梁靜風穩定性的影響。其中較小的攻角主要是考慮大橋所在橋址以及周圍環境，較大的攻角則是考慮一些極端氣候因素以及局地強風影響。不同風攻角下不同風速比值的平均靜風失穩臨界風速如圖15所示。

由圖15可知，不同初始攻角下，非均勻風速來流對橋梁靜風穩定性有著相似的影響，在-2°、0°、+2°、+4°、+8°攻角下，懸索橋的平均靜風失穩臨界風速均隨著風速比值減小而降低，這與前述分析相吻合，也表明了風速非均勻分布不利于流線型箱梁懸索橋抵抗靜風失穩。

5 結論

以某一流線型箱梁懸索橋為背景，采用有限元方法分析了懸索橋在非均勻風作用下的非線性靜風穩定性，得到以下結論：

1）當非均勻風攻角來流作用時，隨著正攻角的增大，橋梁的靜風失穩臨界風速逐漸降低，正攻角會降低橋梁的靜風穩定性。隨著負攻角的增大，橋梁的靜風失穩臨界風速逐步提高，負攻角有利于橋梁的靜風穩定性。通過對比正負攻角的影響程度，發現負攻角對橋梁靜風穩定性的影響程度比正攻角的影響程度大。

2）當非均勻風攻角來流非對稱分布時，由小風攻角確定的橋梁靜風失穩臨界風速可以在一定程度上代表橋梁實際來流情況下的靜風失穩臨界風速;當非均勻風攻角來流對稱分布時，可以選擇平均攻角確定的靜風失穩臨界風速來衡量橋梁的靜風穩定性。

3）非均勻風速來流會降低橋梁的靜風失穩臨界風速，對橋梁的靜風穩定性有不利影響，并且來流風速對稱分布時對該類型橋梁靜風穩定性的影響比來流風速非對稱分布時的影響更大。不同初始攻角下，非均勻風速來流對橋梁靜風穩定性有著相似的影響，懸索橋的平均靜風失穩臨界風速均隨著風速非均勻程度增大而降低。參考文獻：

[1] 陳政清. 橋梁風工程[M]. 北京： 人民交通出版社， 2005.

CHEN Z Q. Bridge wind engineering [M]. Beijing： China Communications Press， 2005. （in Chinese）

[2] ?BOONYAPINYO V， YAMADA H， MIYATA T. Wind-induced nonlinear lateral-torsional buckling of cable-stayed bridges [J]. Journal of Structural Engineering， 1994， 120（2）： 486-506.

[3] 程進， 肖汝誠， 項海帆. 大跨徑懸索橋靜風穩定性的參數研究[J]. 公路交通科技， 2001， 18（2）： 29-32.

CHENG J， XIAO R C， XIANG H F. Parametric studies on aerostatics stability for suspension bridges [J]. Journal of Highway and Transportation Reseach and Development， 2001， 18（2）： 29-32. （in Chinese）

[4] ?CHENG J， JIANG J J， XIAO R C， et al. Advanced aerostatic stability analysis of cable-stayed bridges using finite-element method [J]. Computers & Structures， 2002， 80（13）： 1145-1158.

[5] ?CHENG J， JIANG J J， XIAO R C. Aerostatic stability analysis of suspension bridges under parametric uncertainty [J]. Engineering Structures， 2003， 25（13）： 1675-1684.

[6] ?CHENG J， XIAO R C， XIANG H F， et al. NASAB： A finite element software for the nonlinear aerostatic stability analysis of cable-supported bridges [J]. Advances in Engineering Software， 2003， 34（5）： 287-296.

[7] ?BOONYAPINYO V， LAUHATANON Y， LUKKUNAPRASIT P. Nonlinear aerostatic stability analysis of suspension bridges [J]. Engineering Structures， 2006， 28（5）： 793-803.

[8] 李永樂， 歐陽韋， 郝超， 等. 大跨度懸索橋靜風失穩形態及機理研究[J]. 空氣動力學學報， 2009， 27（6）： 701-706.

LI Y L， OUYANG W， HAO C， et al. Study on shape and mechanism of aerostatic stability for long span suspension bridges [J]. Acta Aerodynamica Sinica， 2009， 27（6）： 701-706. （in Chinese）

[9] ?XU M， GUO W W， XIA H， et al. Nonlinear aerostatic stability analysis of Hutong cable-stayed rail-cum-road bridge [J]. Wind and Structures， 2016， 23（6）： 485-503.

[10] 管青海， 張凱， 李加武， 等. 大跨人行懸索橋非線性靜風失穩發展過程分析[J]. 橋梁建設， 2018， 48（1）： 76-81.

GUAN Q H， ZHANG K， LI J W， et al. Analysis of development process of nonlinear aerostatic instability of a long span pedestrian suspension bridge [J]. Bridge Construction， 2018， 48（1）： 76-81. （in Chinese）

[11] 管青海， 周燕， 李加武， 等. 主跨420 m人行懸索橋非線性靜風穩定影響參數分析[J]. 振動與沖擊， 2018， 37（9）： 155-160.

GUAN Q H， ZHOU Y， LI J W， et al. Effects of parameters on nonlinear aerostatic stability of a pedestrian suspension bridge with main span of 420 m [J]. Journal of Vibration and Shock， 2018， 37（9）： 155-160. （in Chinese）

[12] ZHANG W M， QIAN K R， WANG L， et al. Aerostatic instability mode analysis of three-tower suspension bridges via strain energy and dynamic characteristics [J]. Wind and Structures， 2019， 3（29）： 163-175.

[13] 張文明， 葛耀君. 考慮風速空間分布的三塔懸索橋靜風穩定分析[J]. 東南大學學報（自然科學版）， 2018， 48（1）： 152-156.

ZHANG W M， GE Y J. Aerostatic stability analysis of suspension bridge with three towers considering spatial distribution of wind speed [J]. Journal of Southeast University （Natural Science Edition）， 2018， 48（1）： 152-156. （in Chinese）

[14] ?ZHOU Q， LIAO H L， WANG T. Numerical study on aerostatic instability modes of the double-main-span suspension bridge [J]. Shock and Vibration， 2018， 2018： 7458521-7458529.

[15] 張玉琢， 劉海卿， 馬凱. 大跨徑懸索橋靜風穩定性研究[J]. 遼寧工程技術大學學報（自然科學版）， 2019， 38（3）： 258-262.

ZHANG Y Z， LIU H Q， MA K. Research on aerostatic stability of long span bridge [J]. Journal of Liaoning Technical University （Natural Science）， 2019， 38（3）： 258-262. （in Chinese）

[16] ?DONG F H， CHENG J. A new method for estimation of aerostatic stability safety factors of cable-stayed bridges [J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings， 2019， 172（1）： 17-29.

[17] 胡朋， 顏鴻仁， 韓艷， 等. 山區峽谷非均勻風場下大跨度斜拉橋靜風穩定性分析[J]. 中國公路學報， 2019， 32（10）： 158-168.

HU P， YAN H R， HAN Y， et al. Aerostatic stability of long-span cable-stayed bridge under inhomogeneous wind fields induced by mountain-gorge terrain [J]. China Journal of Highway and Transport， 2019， 32（10）： 158-168. （in Chinese）

[18] ?HU P， HAN Y， XU G J， et al. Effects of inhomogeneous wind fields on the aerostatic stability of a long-span cable-stayed bridge located in a mountain-gorge terrain [J]. Journal of Aerospace Engineering， 2020， 33（3）： 04020006.

[19] 李文杰. 大跨徑懸索橋靜風穩定性分析[D]. 西安： 長安大學， 2009.

LI W J. Study on aerostatic stability of long-span suspension bridges [D]. Xian： Changan University， 2009. （in Chinese）

[20] 張志田， 葛耀君. 基于正交異性殼單元的懸索橋非線性靜風穩定性分析[J]. 中國公路學報， 2004， 17（4）： 64-69.

ZHANG Z T， GE Y J. Nonlinear aerostatic instability analysis of suspension bridges based on orthotropic shell element models [J]. China Journal of Highway and Transport， 2004， 17（4）： 64-69. （in Chinese）

[21] 戴禮勇. 大跨度公鐵兩用懸索橋靜風穩定性研究[D]. 成都： 西南交通大學， 2013.

DAI L Y. Aerostatic stability of long-span combined highway and railway suspension bridge [D]. Chengdu： Southwest Jiaotong University， 2013. （in Chinese）

（編輯 胡玲）