抗風纜對雙塔單跨懸索橋動力性能影響研究

李茂奇

（天津市賽英工程建設咨詢管理有限公司，天津 300051）

橋梁氣動失穩包含靜力失穩和動力失穩，很多懸索橋破壞都為動力失穩[1～3]。在靜風荷載作用下，橋梁整體剛度發生改變，會對動力失穩產生影響[4～5]且懸索橋靜力失穩具有突發性，失穩臨界風速不易確定，是一種脆性破壞[6]；所以，靜風荷載是大跨橋梁設計中不可忽視的因素[7～8]。

本文以某雙塔單跨人行懸索橋為例，建立空間有限元模型，分析抗風纜不同布置形式和不同水平張力對人行懸索橋動力性能及其靜風穩定性能影響，基于懸索橋靜風扭轉發散機理，分析不同抗風纜形式對人行懸索橋靜風穩定性的影響。

1 工程概況

某雙塔單跨景觀人行懸索橋全長160 m，主跨長120 m，橋寬4 m，人行道寬2.5 m。西岸主塔高23.845 m，東岸主塔高29.495 m，上部為2 根矩形塔柱，下部為矩形圓弧截面實體塔柱。塔柱基礎為樁基礎，兩岸主纜錨錠均采用重力式錨。橋墩、錨錠及橋塔采用C40混凝土，加勁梁采用Q345鋼材。見圖1。

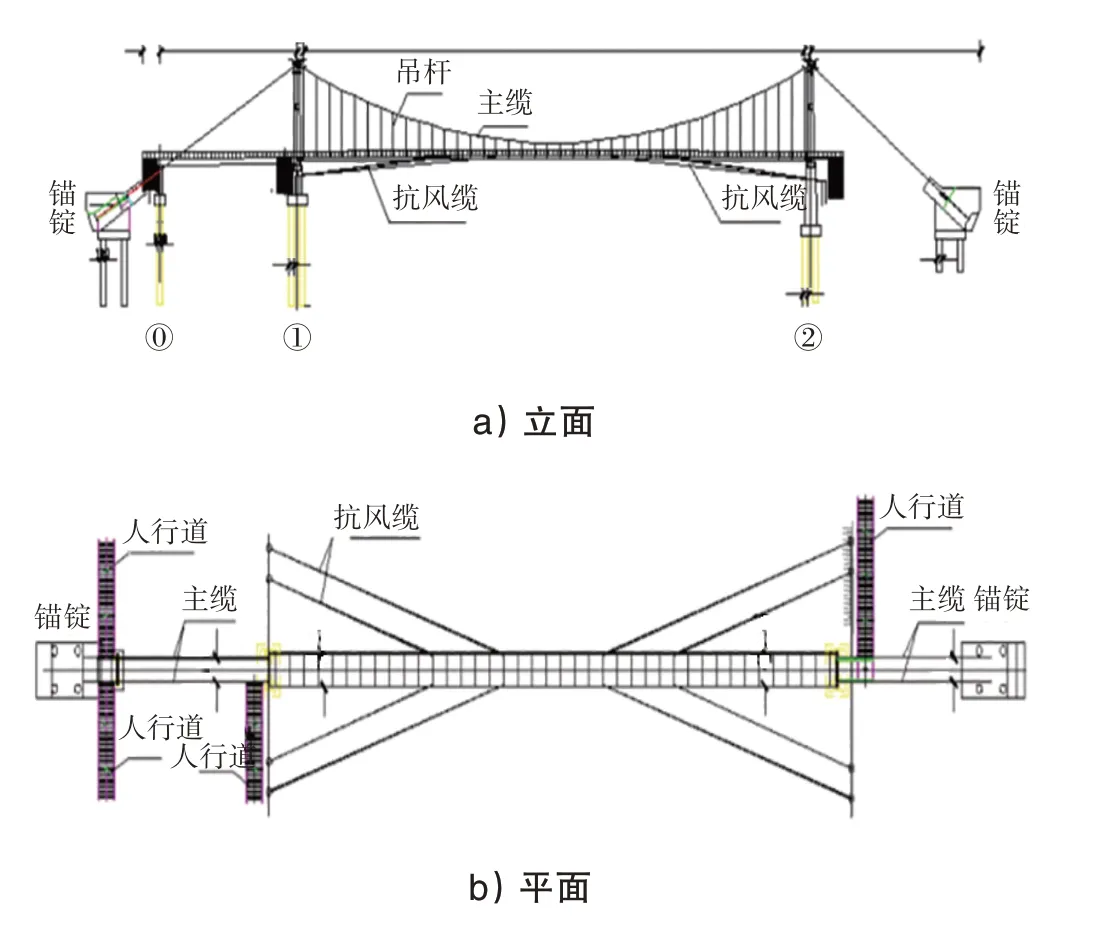
圖1 人行懸索橋

2 抗風纜對結構動力性能的影響

建立空間有限元模型，全橋共234 個節點、362 個單元。主纜、吊桿采用只受拉索單元，主梁、橋塔采用空間桿單元。主纜錨錠處和主塔底端采用固結約束；主纜直接與塔頂節點連接，主梁與主塔下橫梁連接處彈性連接；吊桿直接連接相對應的主纜和主梁節點。見圖2。

圖2 懸索橋有限元模型

2.1 抗風纜布置形式對橋梁動力性能的影響

假定抗風纜所在平面與水平面夾角為θ，抗風纜水平張拉力為30 kN。分別取θ=15°、30°、45°，計算橋梁動力特性，增加抗風纜可以在不同程度上提高關鍵振型頻率。見圖3。

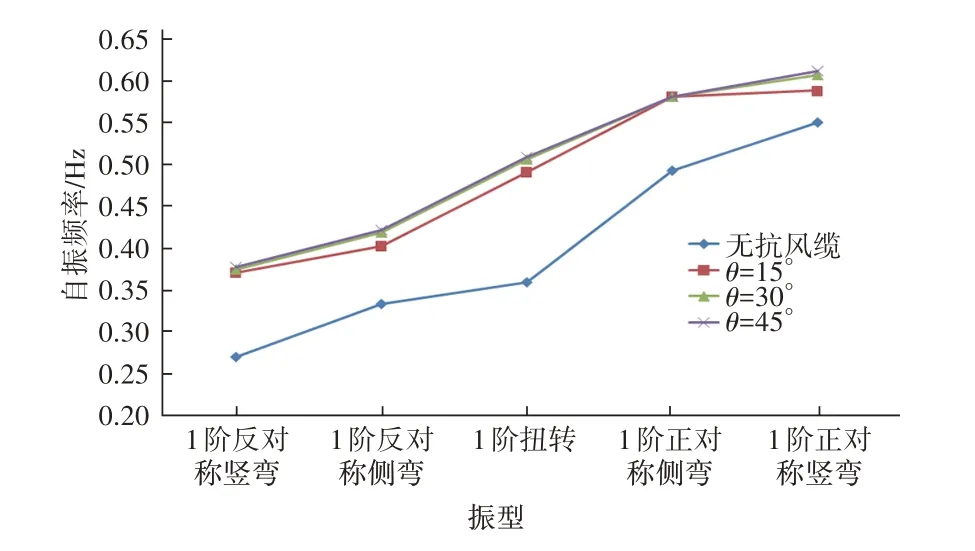
圖3 抗風纜不同布置形式下加勁梁動力特性

當θ=15°時，加勁梁反對稱豎彎頻率提高幅度最大，提高37.55%；θ=30°、45°時，加勁梁扭轉頻率提高幅度最大，分別提高40.95%和41.78%；不同布置形式對主梁正對稱側彎影響不大。經過綜合考慮，本橋采用30°的水平夾角，既可以保證各振型頻率的提高，又可以節約用地和工程造價。

2.2 抗風纜水平張拉力對橋梁動力性能的影響

取θ=30°，分別取水平張力F=5、10、15 kN；增設抗風纜后，無論張拉力多大，橋梁各關鍵振型頻率均有所提高。見圖4。

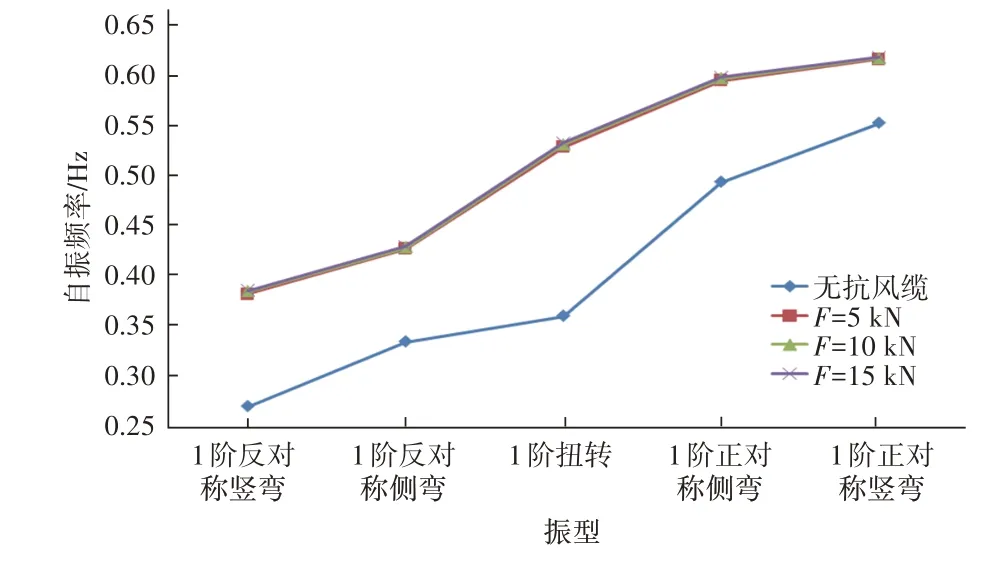
圖4 抗風纜不同水平張拉力下加勁梁動力特性

F=10 kN 時，4 階扭轉振型頻率提高幅度最大，提高了47.91%；F=5 kN 時，7 階正對稱豎彎振型頻率提高幅度最小，提高了11.64%。雖然隨著抗風纜水平張力增加，結構各關鍵振型頻率均有所提高，但是增長幅度均很小，其中增幅最大的為2 階反對稱豎彎和4階扭轉頻率只增加了1.12%和1.11%，可以忽略不計；因此不能通過提高抗風纜的水平張力來提高各關鍵振型的頻率。但是，由于本橋為景觀人行懸索橋，需要綜合考慮景觀效果和行人因張拉力較小而產生不安全心理等因素；本橋將抗風纜的水平張拉力設置為30 kN。

2.3 抗風纜立面傾角對橋梁動力性能的影響

取θ=30°、F=30 kN，計算立面傾角θ′=15°、30°、45°、60°共4種布置形式對橋梁穩定性的影響，隨著立面傾角增加，橋梁頻率隨之增大。見圖5。

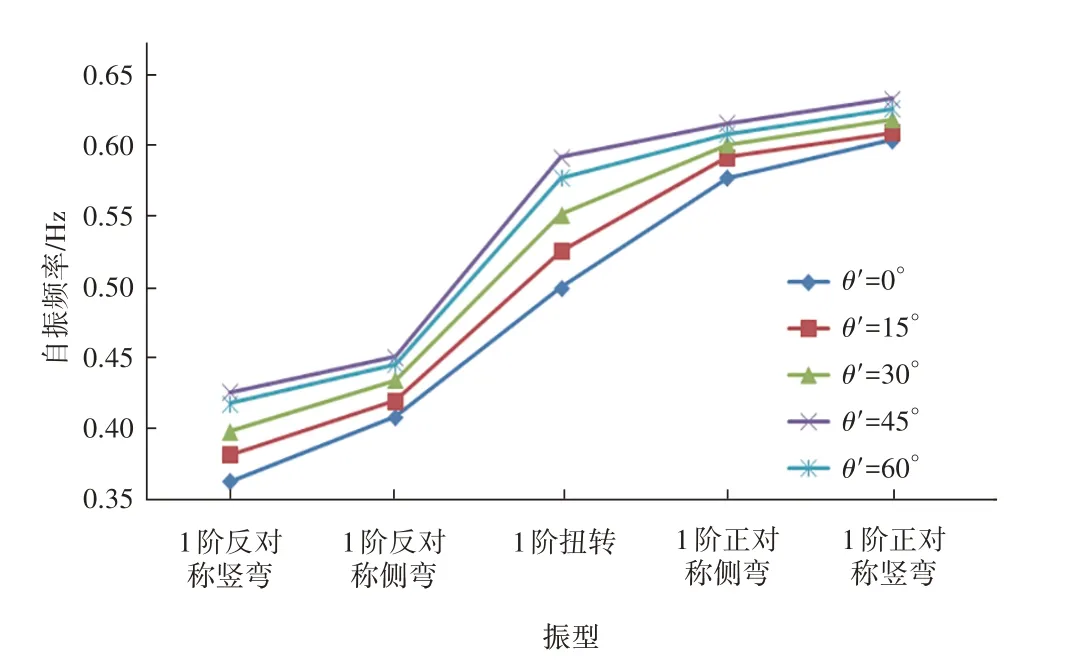
圖5 抗風纜不同立面傾角情況下加勁梁動力特性

θ′=15°時，各振型提高幅度均＜5%；當θ′由15°增加到45°時，各振型頻率提高幅度較快，扭轉頻率最大提高16.60%，反對稱豎彎提高16.31%；當θ′達60°時，反對稱豎彎頻率提高14.17%，扭轉頻率提高14.82%，與θ′=45°時相比，各頻率提高幅度均有所減小。由此可知，θ′=45°時穩定性最好。當θ′由30°增加到45°時，雖然2 階反對稱豎彎和4 階扭轉兩者增加較大，但是增加值僅為6.62%和6.12%，其他振型增加值均＜5%，對提高該橋的動力性能影響較小。因此，在綜合考慮施工現場和工程造價的基礎上，將豎向傾角設置為30°。

3 抗風纜對橋梁靜風穩定性的影響

3.1 抗風纜布置形式的影響

對抗風纜和加勁梁主梁水平夾角δ=15°、30°、45°進行靜風穩定性分析（風攻角取0°），其中側傾失穩主要考慮阻力因素，扭轉失穩主要考慮升力矩因素。

3.1.1 對橋梁橫向位移影響

抗風纜不同布置形式下橋梁橫向位移見圖6。

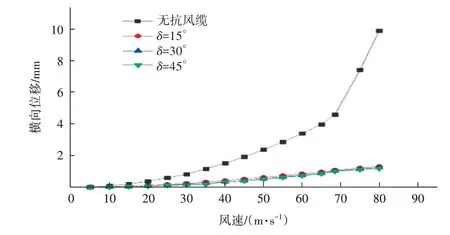
圖6 抗風纜不同布置形式下橋梁橫向位移

無抗風纜時橋梁側傾失穩發散臨界風速為68 m/s，該地區已知最大風速48 m/s，側傾失穩風速超過該地區已知最大風速，取風速50 m/s。δ=15°、30°、45°對應50 m/s 風速時結構橫向位移較無抗風纜分別減小73.48%、77.72%、78.26%，當δ=45°時，橋梁橫向位移提高幅度最大，但與δ=30°時相比，僅提高0.54%，提高幅度可忽略不計；但當δ=45°時，所需要的空間比δ=30°時大，布置時易受空間限制。結合抗風纜對動力性能的影響研究的結果和現場施工場地，選擇30°的水平夾角布置抗風纜更合適。

3.1.2 對橋梁豎向位移和扭轉位移影響

不同抗風纜布置形式下，迎風面主纜中點的豎向位移和加勁梁中點的扭轉位移見圖7和圖8。

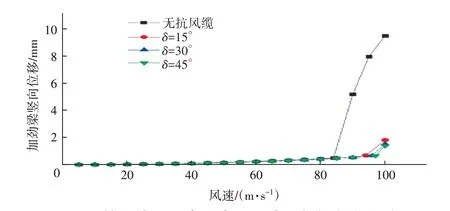
圖7 抗風纜不同布置布置形式下橋梁豎向位移

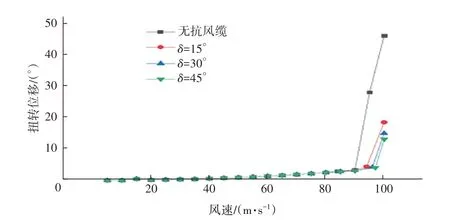
圖8 抗風纜不同布置布置形式下橋梁扭轉位移

無抗風纜時扭轉發散臨界風速為84 m/s，3 種抗風纜布置形式對應的扭轉發散臨界風速分別為94、96、97 m/s，均提高10%以上。當風速為扭轉發散臨界風速84 m/s 時，3 種抗風纜布置形式的橋梁豎向位移對應無抗風纜情況分別減小2.4%、4.2%、6.0%，扭轉位移分別減小1.0%、1.8%、5.3%。橋梁設置抗風纜不僅可以提高扭轉發散臨界風速，還可減小同等風速下豎向位移和扭轉位移。雖然δ由30°增加到45°時，豎向位移和扭轉位移均有所減小，但是減小幅度均不大，結合對動力性能影響的研究，選擇30°的水平夾角更合適。

3.2 抗風纜水平張力的影響

取δ=30°，分別計算抗風纜水平張力F=5、10、15 kN3種工況下橋梁靜風穩定性能。

3.2.1 對橋梁橫向位移影響

不同抗風纜水平張力下迎風面主纜中點的橫向位移見圖9。

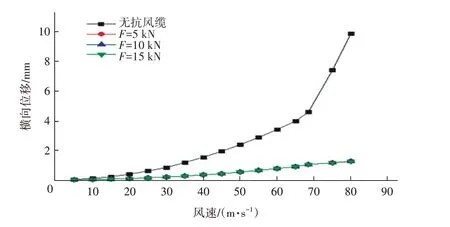
圖9 不同張拉力抗風纜作用下橋梁橫向位移

3 種方案的加勁梁橫向位移相比無抗風纜時均減小77.8%，橋梁靜風穩定性顯著增強。在風速＜80 m/s 時，F由5 kN 增加到15 kN 對加勁梁橫向位移沒有影響。綜合考慮動力性能、景觀效果和因張拉力過低給行人產生的不安全心理影響，水平張拉力設置為30 kN。

3.2.2 對橋梁豎向位移和扭轉位移影響

主纜中點的豎向位移及加勁梁中點的扭轉位移見圖10和圖11。

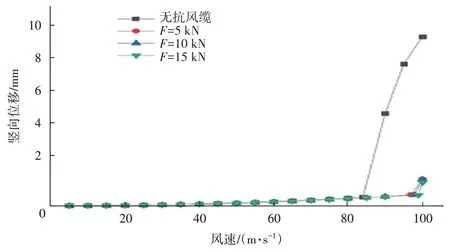
圖10 不同張拉力抗風纜作用下橋梁豎向位移

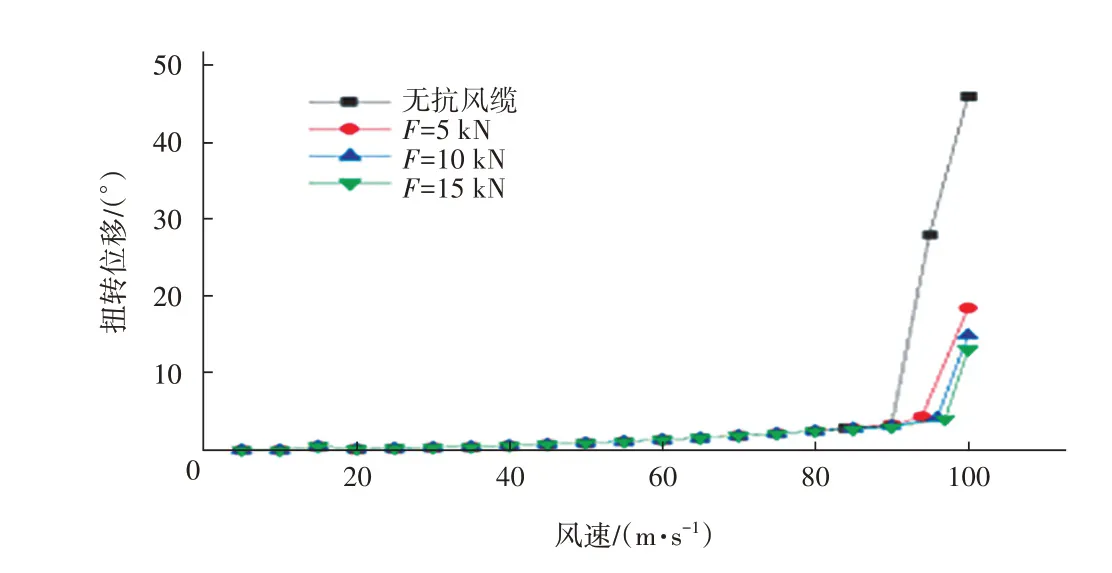
圖11 不同張拉力抗風纜作用下橋梁扭轉位移

不同張拉力抗風纜作用下扭轉發散臨界風速分別為97、98、99 m/s，相比無抗風纜時的84 m/s 均提高10%以上，橋梁靜風穩定性顯著增強；而F由5 kN 增加到15 kN，臨界風速只提高2 m/s 左右，表明增加抗風纜水平張力對提高結構靜風穩定效果并不明顯。當風速為扭轉發散臨界風速時，不同抗風纜布置形式的橋梁豎向位移比無抗風纜減小均＜5%，表明增加抗風纜水平張力對減小豎向位移效果不明顯。由于本橋為景觀人行懸索橋，需要考慮景觀效果和行人因張拉力過低而產生不安全的心理影響，抗風纜的水平張拉力設置為30 kN。

4 試驗結果與理論計算結果對比

考察橋梁在正常使用荷載作用下的力學性能，對該懸索橋主跨進行靜力試驗。選擇懸索橋跨中作為控制截面，采用水箱滿布加載方式，只設置一種工況，分3級均勻加載。撓度測點主要布置在加勁梁主跨各24 分點的橋面中軸線處。各級加載作用下的實測撓度值與理論計算值見圖12。

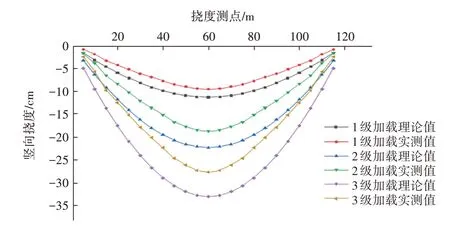
圖12 各級加載作用下橋梁實測撓度值與理論計算值

試驗荷載作用下，在3級加載過程中，最大位移均出現在跨中60 m 測點處。3 次加載橋梁實測位移均小于理論計算值，說明懸索橋實際抗力大于設計值且各測點位移趨勢實測值與理論計算值吻合，說明理論計算結果可以較好反應橋梁實際情況。

5 結論

1）增加抗風纜可在不同程度上提高關鍵振型頻率。當θ=15°時，加勁梁反對稱豎彎頻率提高幅度最大，隨著角度變化，主梁反對稱豎彎頻率變化很小；θ=30°、45°時，加勁梁扭轉頻率提高幅度最大；3 種布置形式對主梁正對稱側彎改變不大。

2）抗風纜施加水平張力可大幅提高橋梁各關鍵振型頻率。隨抗風纜水平張力增加，結構各關鍵振型均有所提高，但增幅不大。

3）抗風纜立面傾角可提高橋梁關鍵固有頻率。隨著抗風纜立面傾角增加，橋梁抗風穩定性增加，立面傾角超過45°，隨著立面傾角增大橋梁抗風穩定性降低。但是立面傾角由30°增加到45°時，各振型頻率提高幅度較小，對提高該橋的動力性能影響較小。

4）設置抗風纜可增強結構抗風穩定性能，減小其相同風速下側傾失穩橫向位移和扭轉失穩時的豎向位移和扭轉位移，其中抗風纜與加勁梁夾角為45°時對結構位移影響最大；由30°增加到45°時，豎向位移和扭轉位移均有所減小，但是減小幅度均不大。

5）在一定范圍內，抗風纜水平張力增加對結構位移影響不大，只需合理選擇抗風纜張力值，即可提高人行懸索橋靜風穩定性。

6）景觀人行懸索橋設置水平張力時，還要考慮景觀效果和行人心理安全等因素的影響。