數字信號處理技術在地基動力參數測試中的應用
孫 銳
化學工業第一勘察設計院有限公司 河北滄州 061001
動力機器的動荷載必然會引起地基及基礎的振動,從而可能產生一系列不良影響。因此,動力機器基礎設計應滿足下列基本要求:不應產生影響機器正常使用的變形;基礎本身應具有足夠的強度、剛度和耐久性;不產生影響工人身體健康、妨礙機器正常運轉和生產,以及造成建筑物開裂和破壞的劇烈振動;基礎的振動不應影響鄰近建筑物、構筑物或儀器設備等的正常使用。動力基礎設計成功與否的關鍵步驟之一就是確定地基動力參數。
1 地基動力參數測試機理
對于實體基礎振動計算,目前主要有質量- 彈簧-阻尼器模型理論及剛體- 半空間模型理論,我國目前工程多采用質量- 彈簧- 阻尼器的計算模型。質量- 彈簧- 阻尼器理論:假設基礎為無彈性的質量,地基為無質量的彈簧,基礎受垂直擾力Pssinwt 作用時,基礎產生的慣性力與基礎振動加速度成正比例,阻尼力與振動速度成正比例,地基的反力與振動位移成比例。其力學模型如圖1 所示,公式見式(1)。
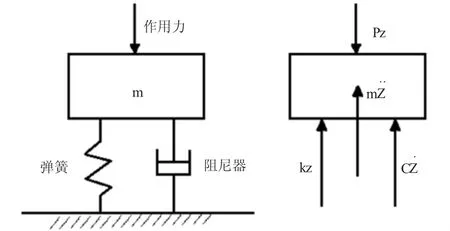
圖1 質量- 彈簧- 阻尼器理論示意圖
用質量- 彈簧- 阻尼器理論進行機器基礎動力分析時,要提供地基土的地基剛度、阻尼比等動力參數,這需要在現場進行塊體基礎動力測試,以滿足設計需要。一般做法是在現場澆筑模擬基礎,在基礎上安裝激振器和拾振器,通過激振器對基礎施加不同頻率的激振力,通過拾振器測出對應的基礎振幅。圖2 為現場地基動力參數測試示意圖。
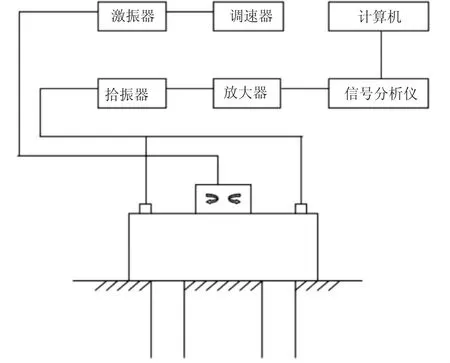
圖2 現場地基動力參數測試示意圖
通過計算求出設計所需的動力參數。依據《地基動力特性測試規范》及《巖土工程勘察規范》及設計要求,數據處理應得到幅頻響應曲線:豎向振動線位移隨頻率變化的幅頻響應曲線;水平振動線位移隨頻率變化的幅頻響應曲線,以及基礎頂面測試點由回轉振動產生的豎向振動線位移隨頻率變化的幅頻響應曲線;基礎頂面測試點在扭轉力矩作用下的水平振動線位移隨頻率變化的幅頻響應曲線。
2 行業現狀
以往試驗多采用儀器采集數據后人工量波的方法來獲得幅頻響應曲線。如果某一頻率采集到的測試信號有8個極大值、8 個極小值,應該用8 個極大值的平均值減去8個極小值的均值,得到振幅;8 個極大值或極小值的長度即7 個波經歷的時間,通過換算可以求得對應頻率。當然也可用頻譜分析方法求得頻率。當頻率改變,需要再重復這些步驟,依次獲得幅頻響應曲線。如果收集到的測試信號由更多數據形成,則數據處理量又會成倍增加。所以該手段費時、費力、誤差大。另外,測試信號存在高頻或低頻干擾,如何準確確定頻率及振幅也存在一些具體問題。再次,現場實際測試時,需要找到共振峰,但共振峰對應頻率相對較高,測試基礎振幅較大,數據較難獲得。為減少人工量波數據計算中的勞動強度,提高計算精度和工作效率,需要通過數字信號處理技術來解決上述問題。
3 設計思路
數字信號處理主要包括數字濾波、數據截斷、加窗、頻域分析和奇異點剔除等。
3.1 濾波處理
對測試數據進行低頻和高頻干擾進行平滑濾波,提高有用信號的計算精度。
3.2 計算頻率值
頻率值計算的基本原理:利用信號傅立葉變換具有的信號時域與頻域之間的對應關系,建立信號的DFT 與四種信號頻譜之間的關系。
設時間域某一窗口寬度(采樣數據個數)為N,采樣頻率為CYPL,則對該數據段作快速傅里葉變換,尋找幅度譜中的極值。設在N 個變換的數據中,第SK 值最大,則即可求得該數據段的振動頻率,見式(2)。由式可知,頻率域的采樣精度與時間域的CYPL 成反比,與樣本數N成正比。由于須滿足采樣定律,同時提高時間域的振幅精度,CYPL 不能太低,只能提高N 來提高頻率域的頻率精度,即在N 個采樣數據兩邊補充0。假使將當前數據的頻率精度提高10 倍,即需在N 個采樣數據段前后各補充5N 個0。若對10N 個采樣數據進行快速傅里葉變換,則計算量增加很多,降低了計算速度。因此,在程序設計時,先對N 個樣本值作快速傅里葉變換,尋找極值SK。實際振動頻率與SK 推算出的振動頻率相差不大,只需對SK附近的幾個數據作精確計算,作傅里葉變換,即可精確求得振動頻率。這樣即不影響計算速度,又提高了計算精度。
F=SK×CYPL/ N。 (2)
時間域窗口寬度N 相當于對信號進行加窗處理,即將信號乘以時域的有限寬矩形窗函數,采樣后信號x(t)g(t)經截斷成為x(t)g(t)w(t),見式(3)。
由數值分析原理可知,信號截斷會造成能量泄露問題,如余弦函數信號主頻為f0,截斷后經過傅里葉變換的幅度譜出現....- 3f0、- 2f0、- f0、f0、2f0、3f0……等多個極值用圖形表示信號的截斷、能量泄漏現象。提高截斷信號長度,即提高矩形窗寬度可減小泄漏,此時sinc 函數主瓣變窄,旁瓣向主瓣密集,由于旁瓣衰減較快,故可減小泄漏。但顯然采樣點數隨之提高,增加計算負擔。此外,還可以采用其他窗函數。一個好的窗函數,其主瓣應盡可能窄(提高頻率分辨力),旁瓣相對于主瓣盡可能小,且衰減快(減小泄漏)。幾種典型窗函數的技術指標見表1。分析可知,漢寧窗是比較適宜的加窗函數,當然也可根據不同情況選擇不同的加窗函數。
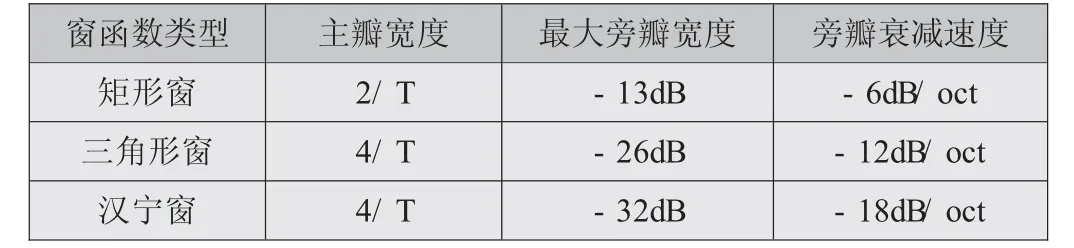
表1 幾種典型窗函數的技術指標
3.3 計算振幅值
由已求出的該數據段振動頻率,可求得振動周期。假使此數據段有n 個振動波段,分別對每個波段采用篩選法,尋找極大值、極小值和該振動波段的振幅;將n 個振動周期的振幅求平均值,即為該數據段的振幅值。
3.4 多窗口寬度
可將測試數據分為不同的數據長度:512 點、256 點、128 點和自動窗口寬度。自動窗口寬度是指在轉換數據過程中窗口寬度并不固定,而是將上一數據段的10 個振動周期作為下一數據段的長度。此種方法的優點是在振動頻率較高時,所獲得的幅頻響應曲線計算精度較高。
3.5 得到測試成果
依次對數據的各段作頻率和振幅計算,從而得到幅頻響應曲線,在幅頻響應曲線上依據規范選取數值計算,即求得測試成果,如圖3 所示。
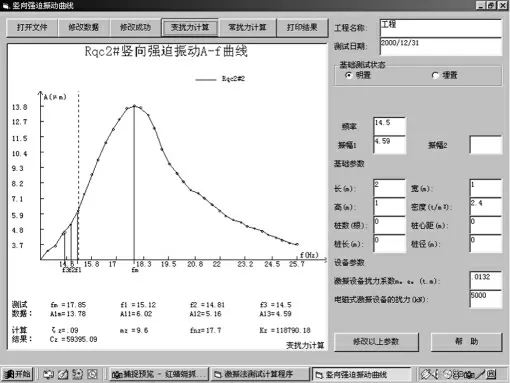
圖3 計算成果輸出示意圖
4 應用實例
應用以上思路編制了激振法測試數據處理系統軟件,該程序于2001 年編制完成,先后在南京揚子乙烯擴建(樁基)、德州華魯恒升大氮肥擴建(天然地基)內蒙神華煤液化(天然地基、樁基)和天津渤化石化有限公司60 萬t/ a丙烷脫氫(樁基) 等工程中得到驗證,取得良好的效果。2013 年,該軟件通過國家版權局頒發的計算機軟件著作權登記證書。
5 結語
數字信息處理技術與以往傳統的資料解釋方法相比,具有以下優點:
(1)大大降低了技術人員資料解釋的工作量,如一個塊體基礎測試數據采用人工量波法時,需要多名技術人員相互配合計算4~5h,而用該程序只需0.5h。
(2)提高了計算精度,人工量波存在測量誤差,而使用而該程序不存在此影響因素。
(3)計算機自動計算打印輸出成果曲線,方便且美觀。而以往需人工畫圖、手工計算。

