圓端形橋墩布置對河道墩前壅水影響分析

魏 帥，李 昂，陶伯鈞

(1.水發規劃設計有限公司，山東 濟南 250013；2.濟南大學水利與環境學院，山東 濟南 250022)

1 研究背景

在高速鐵路建設中，為保證路線盡量順直，穿越河流需要在河道中布置橋墩。但橋墩的布置會縮小過流斷面，進而引起橋梁斷面上游洪水位升高，進而對上游河道防洪和兩岸居民的安全造成不利影響。

隨著數值模擬方法的不斷進步，通過水動力學模型進行河道中橋梁壅水模擬和分析已經成了認識和解決橋梁阻水問題的常見方法。袁曉淵針對淮河入海水道鐵路橋通過SMS軟件定量分析了不同形狀和尺寸的橋墩對于橋梁上游水位的影響，并將其作為橋梁設計和防護的參考依據。郭婭等對比分析了一維水動力學軟件Mike11與經驗公式在橋梁防洪影響分析中的區別，并應用在赤化大橋洪評項目中。閆杰超等基于動量守恒原理，通過CFD軟件對雙樁橋墩的阻水效應和用水特性進行了研究，并提出了理論公式。鮑瑞雪等利用VOF三維數學模型對復雜地形上的群墩阻水效應和涌浪等進行了分析。Zhang等分析了恒定流條件下相鄰樁之間的水流流動機理，討論了樁間距對于流場的影響。Liu等通過數值模擬研究了圓形樁周圍的局部水流流動情況，結果顯示兩個樁之間的間隙比對流場有明顯的影響。高原等、張震、焦顯松、于冬、劉洪昌、金相楠等分別針對西法城際鐵路眉縣跨渭河特大橋、商合杭鐵路淮河大橋、兜兒寺大橋、白沙河河道城市斜交橋、永新特大橋、順河跨海大橋中橋墩對水面壅高和沖刷等作用進行了數值模擬，對二維數學模型的工程實際應用價值進行了討論。可見，數值模擬技術在分析橋墩影響下水流狀態，減少自然災害和工程事故等方面起到了重要的作用。

2 橋墩數值模型的建立與驗證

2.1 流體運動基本方程

本研究通過數值水槽模擬寬淺型河道中水流的運動規律。

(1)連續性方程

對于連續流體，其在河道中的運動狀態可以通過連續性方程進行概化：

(1)

(2)動量守恒方程

對于運動流體，分別考慮在x和y方向的作用力，表面力可以表示為流體微元在x和y方向所有正應力和切應力之和，表達式如下：

(2)

(3)

式中，H—總水深，H=ζ+h，m；h—時變水深，m；ζ—水面高程，m；p、q—x，y方向單寬流量，m3/(s·m)；C—謝才系數；g—重力加速度，m/s2；f—科氏力系數；ρ—水的密度，kg/m3；W、Wx、Wy—風速及在x，y方向上的分量；fw—風阻力系數；τxx、τxy、τyy—各方向的有效切應力，N。

2.2 數值水槽設計及網格劃分

為簡化計算，突出橋墩布置對于水流流態和橋前壅水的影響，水槽形式為順直型明渠，斷面形式為矩形，水槽長1000m，矩形斷面底寬100m。水槽形式如圖1所示。

圖1 數值水槽模型示意圖

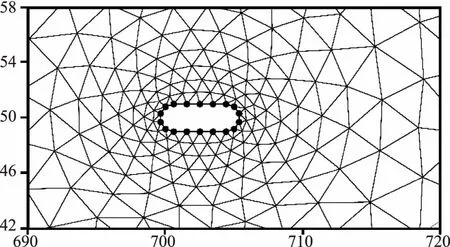
圖2 數值水槽網格

2.3 模型驗證

橋墩采用圓端形截面墩，計算時將橋墩附近網格適當加密，橋墩附近最小網格邊長為0.5m，水槽最大網格邊長10m，計算網格數為13770個。典型網格分布如圖2所示。

4.積極爭取，落實省級土地確權經費。在咨詢部農墾局、部分兄弟墾區、相關測繪公司的基礎上，經反復與省財政廳協商，省農業廳在2017年向省政府提交了《關于申請農墾國有土地使用權確權登記發證工作所需經費的請示》，并在2018年年初落實了土地確權登記發證工作省級財政補助經費318.25萬元，其補助標準是按照山西省農村土地承包經營權確權登記領證工作每畝15元標準的基礎上，考慮到需確權發證的19個農場多為貧困農場且處于貧困縣的實際，又增加了工作經費19萬元。為確保資金安全、快速使用到土地確權發證工作上，省農業廳與國土廳多次溝通論證，于2018年5月底將資金從省農業廳全部撥付到各市農委（畜牧局）。

為保證所建立水動力學模型的可靠性和合理性，需對模型進行驗證。采用Roulund水槽試驗結果對本研究建立的模型進行驗證。

驗證使用的數值模型與Roulund水槽試驗模型一致，長10m，寬3.6m，縱比降0.000117，糙率為0.022，水深0.54m，圓樁直徑0.536m，置于水槽中心，均勻流流速0.326m/s。采用三角形網格進行模擬并對樁柱附近進行網格加密，試驗模型如圖3(a)所示。對比模擬與試驗結果如圖3(b)—3(c)所示，可以看出二者基本吻合，通過二維水動力數值模擬方法進行壅水分析是合理的。

3 橋墩壅水效應數值模擬

為研究橋墩布置對于橋前壅水和水流流態的影響，本文從橋梁與河道交角、橋墩跨度和橋墩軸線與橋梁軸線夾角3個角度進行分析和討論。

3.1 橋梁與河道交角的影響

為討論橋梁和河道交角α對橋前壅水水位的影響，分別對單墩和三墩在交角為0°、2°、5°、10°、30°、45°、60°、75°時河道中水位壅高情況進行模擬，河道中三墩布置時不同橋墩之間的跨度控制在30m。

如圖4所示為不同角度在此情況下橋墩最大壅水值的變化趨勢。當橋墩斜交布置時，橋墩墩前壅水高度較正交時有較大幅度增加，隨后隨著斜交角度的增大，橋梁壅水高度逐漸增加；當斜交角度增大到30°～60°時，橋前壅水高度隨角度增加值明顯。此外，當河道斷面中布置多個橋墩時，由于橋墩對于河道中過流斷面面積的影響以及對于水流流動的干擾，橋墩達到最大壅水值。

如圖5所示為不同角度三橋墩布置時橋墩前約100m內的壅水高度變化的趨勢圖。由相應圖表可知，橋前壅水高度主要表現在橋前50m范圍內。在橋前50m范圍外，水流有一定壅水表現，但壅水高度較小，變化趨勢不明顯；同時由于橋墩對水流的干擾作用，墩前水位表現出一定的起伏，斜交角度越大，橋前水位的干擾作用越大，表現為橋前水位的波動越大。

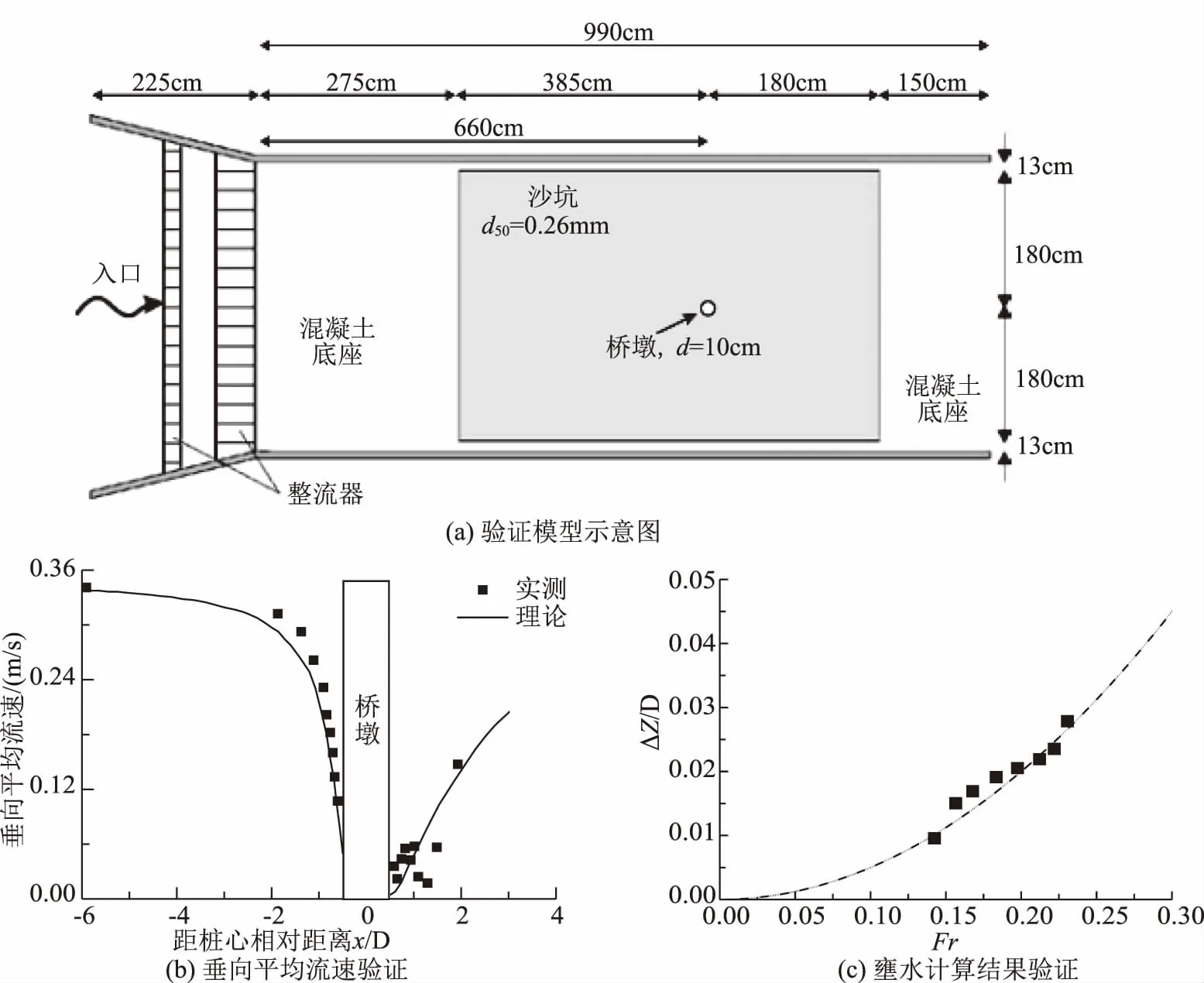
圖3 模型驗證

圖4 不同斜交角度橋前壅水水位

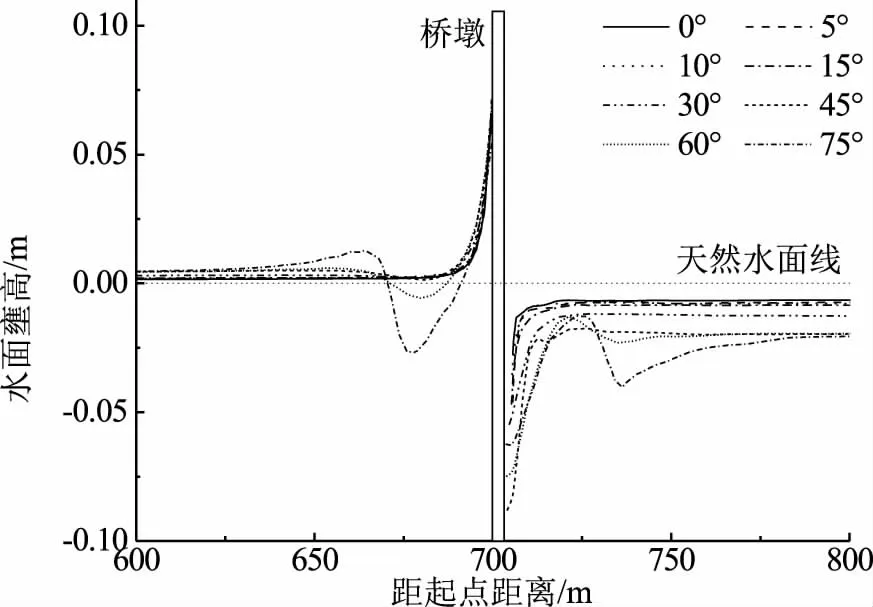
圖5 不同斜交角度時橋墩中軸線水位變化趨勢

3.2 橋梁跨度對橋前壅水的影響

為研究不同跨度橋前壅水水位的影響，選取16、32、40m三種跨度和0°、10°、30°、45°、60°五個斜交角度。不同工況下斜交橋墩的壅水高度如圖6所示，可以看出：無論橋跨如何變化，橋墩壅水高度隨著橋墩斜交角度的增大而增大。

當多橋墩布置在河道中時，橋墩之間的壅水會形成縱向的壅水疊加效應。在斜交角度小于10°時，橋墩橫向距離變化較小，此時橋墩壅水相互影響程度基本保持不變，故橋墩壅水高度變化較小。當橋墩角度自10°角增加時，橋墩壅水的橫向距離繼續變小，且此時橋墩單墩布置發生變化，橋墩壅水值有一定增加；當橋墩角度自30°角增加時，由于橋墩壅水的前后疊加效應，此時上游橋墩的壅水值和壅水范圍明顯高于下游橋墩的壅水值和壅水范圍；相同角度時若橋墩跨度增加，橋墩的疊加效應減弱，橋墩相互間的壅水高度和壅水范圍差距減小。當橋墩斜交布置于河道中時，橋墩的有效阻水面積界于端部截面與投影截面之間。根據投影斷面的壅水計算分析，當橋墩斜交角度較小時，可視有效阻水面積與橋墩的投影截面近似。

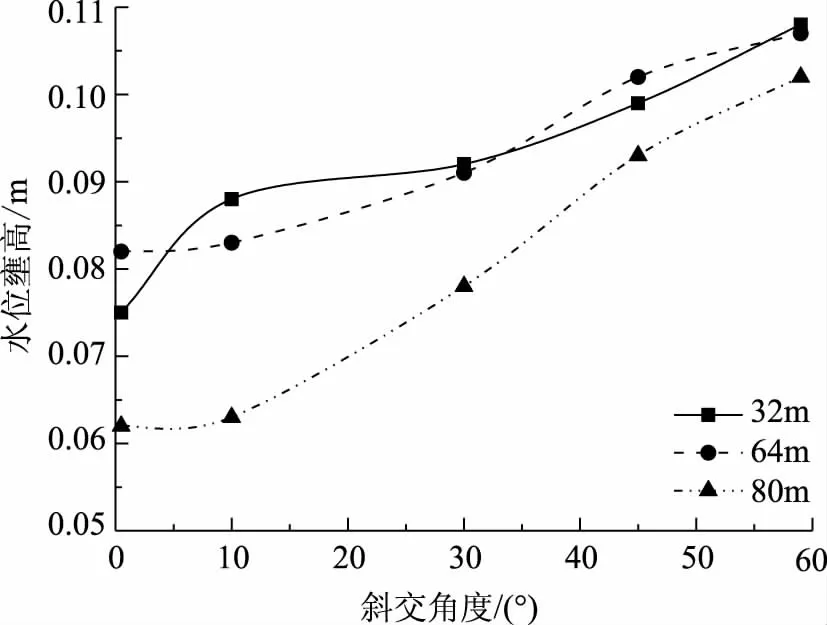
圖6 不同跨度時橋墩中軸線壅水高度變化趨勢

3.3 橋墩布置方式影響

為了研究不同橋墩布置方式對于橋前水位的影響，選擇跨度為30m，角度分別為0°、5°、10°、15°、30°、45°、60°、75°、90°等工況，不同橋墩布置方式如圖7所示，對橋前壅水的影響進行分析。

根據圖7中的布置方案，不同橋墩布置方案對應的河道中最大壅水高度變化規律對比如圖8所示。從圖8中可以看出，隨著橋梁與河道的交角增大，橋墩垂直橋梁布置時河道中最大壅水高度整體呈線性增加，而橋墩平行水流方向布置時橋前最大壅水高度整體不變且略有減小。如圖9所示為典型工況下河道中水流流速和河道水位的分布情況。受橋墩的影響，水流在橋墩處發生繞流。當橋墩與橋梁軸線垂直布置時，隨著角度的增大迎水面面積增大，對水流的阻礙作用和對流向的改變越明顯；對于平行水流布置的橋墩，其阻水面積并未增大，且由于橋墩前后布置帶來的水流橫向干擾減小，橋前壅水水位也相對降低。另外，根據許棟等的研究，將橋墩群看成起阻礙作用的多孔介質，軸線與水流方向平行布置的橋墩其過流斷面面積小，過流能力較強，對水流的阻礙作用相對減弱；斜交布置的橋墩，其過流路徑加長，過流能力也相對減弱，導致壅水相對增加，橋前壅水水位也增大。

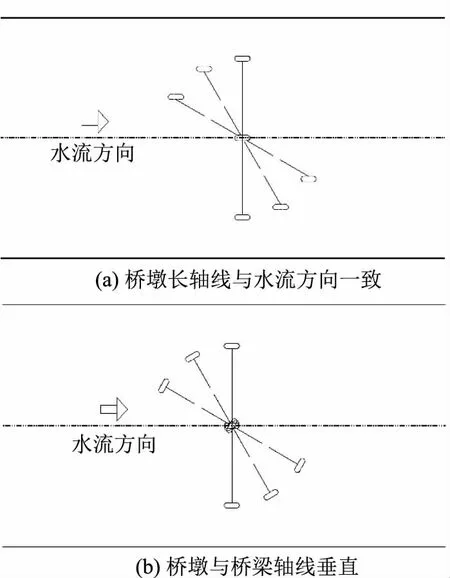
圖7 橋墩布置方案示意圖

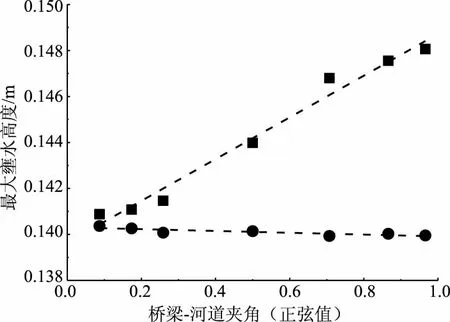
圖8 橋梁-河道夾角對壅水高度的影響

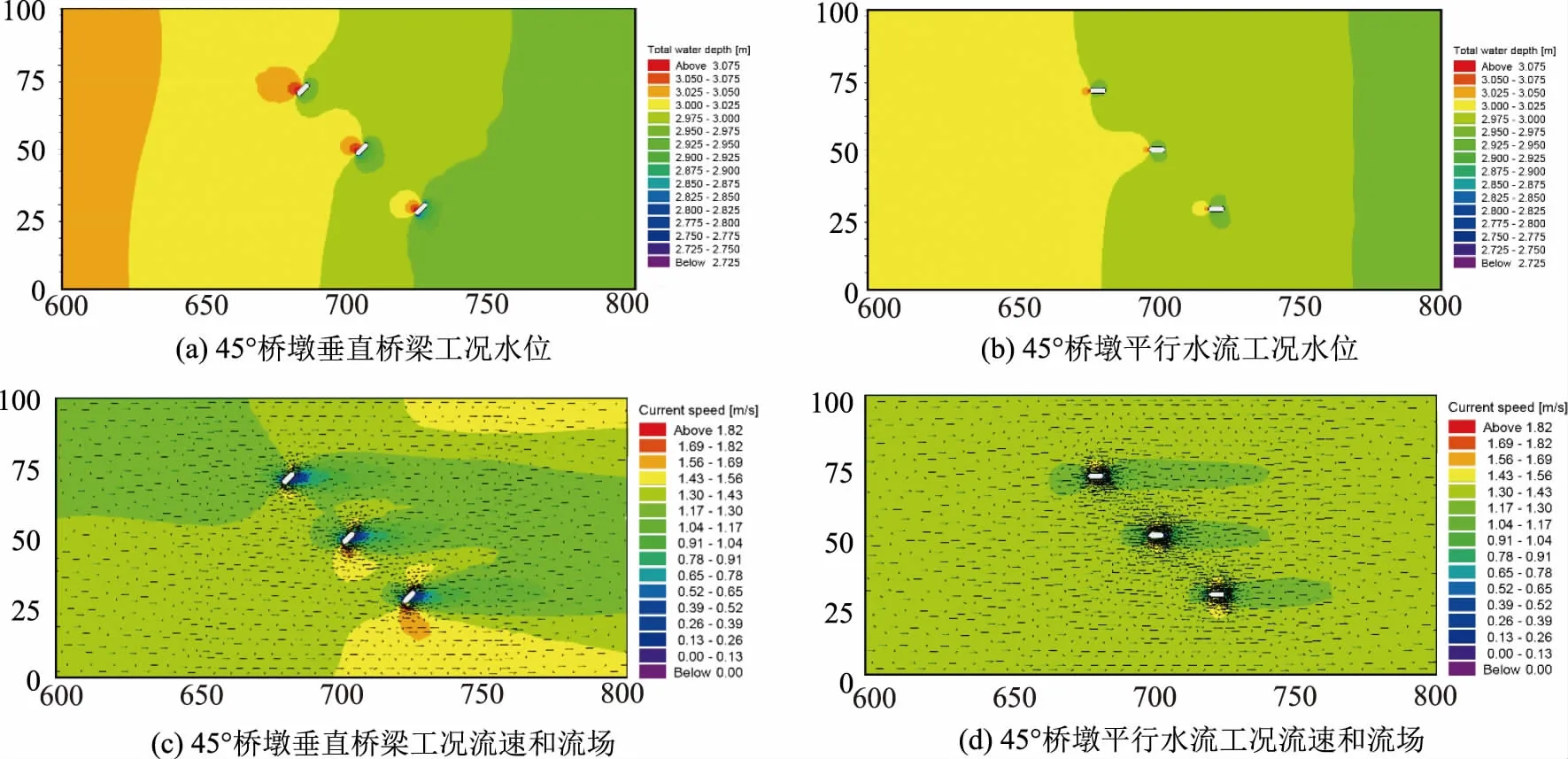
圖9 典型工況下河道水位、流速、流場分布圖

4 結論

本文基于二維水動力數值模擬方法模擬了不同橋墩布置型式下墩前壅水高度的變化，得到以下結論：

(1)橋墩與河道斜交時，壅水高度隨著斜交角度的增大而增大。斜交角度較小時，橋墩的壅水高度增加幅度不明顯；斜交角度越大，墩前壅水高度變化越明顯。多橋墩阻水時墩前壅高高于單個橋墩。

(2)多橋墩布置存在壅水疊加效應。橋墩數量相同，橋墩跨度增加則墩前水位壅高降低。同時，斜交角度增大，橋墩斜向影響增大，橋墩的壅疊加效應更明顯。

(3)橋墩順水流布置可以減少橋墩處水流流速和橋前水流波動。