基于自選尾數壓縮的高能效浮點憶阻存內處理系統

丁文隆 汪承寧,2 童 薇,2

1(華中科技大學計算機科學與技術學院 武漢 430074)

2(武漢光電國家研究中心(華中科技大學) 武漢 430074)

在科學與工程領域中，許多復雜的模型都會用線性系統Ax=b的形式表達[1]，其中，A通常是一個龐大的高精度浮點稀疏矩陣[2].在這樣的系統上進行求解會消耗大量時間與計算資源[3].目前主流的求解大規模稀疏線性系統的方法是克利洛夫(Krylov)子空間方法[1].該方法的求解過程涉及大量的矩陣向量乘法(matrix-vector multiplication, MVM)計算，所以改進MVM的計算模式是節省運算能耗與運算資源的關鍵途徑.

近年來，關于用憶阻陣列進行原位MVM運算的有關加速器被不斷地提出.最先提出的是一類用于執行機器學習和圖形處理任務的憶阻加速器，它們通過向憶阻陣列施加電壓，在陣列上原位地執行MVM運算[4-10].然而，這些憶阻加速器只提供8～16 b的計算，顯然不支持一些以高精度浮點數為主的計算應用.于是，最新的研究提出了將IEEE-754雙精度浮點數部署在陣列上的方式[11].該研究將浮點數的53 b尾數(包括前導1)分位片地部署到不同的陣列上，最后通過乘加縮減樹整合不同位片的結果，實現高精度浮點數運算.

然而，目前仍然沒有任何工作提出在一個系統內，能夠為不同精度的應用提供計算能耗優化的方法.本工作致力于提出一個基于憶阻陣列的模擬MVM運算系統，既能夠為精度較高的應用提供無損的浮點數計算模式，又能夠讓較低精度的應用執行低能耗開銷計算.具體地，本文工作的貢獻主要有4個方面：

1) 設計了一種自選尾數壓縮機制，對于某些低精度的求解應用，可以在陣列運算中選擇性地忽略激活若干權值較小的低位陣列，從而保證在滿足具體任務的求解精度的前提下，減少運算陣列以及外圍電路的能耗.同時提出了一種動態的對齊位優化機制，摒棄原有的靜態對齊位的設定模式，根據矩陣實際指數范圍的要求來設置參與運算的對齊位陣列，減少冗余對齊位帶來的能耗.

2) 針對于尾數壓縮和對齊位優化策略，提出了一種葉子結點數可變的流水乘加縮減樹的結構.解決了激活運算的陣列數不確定所帶來的偏移策略失效以及無法進行流水的問題.這種新型的乘加縮減樹結構能夠在激活任意數量的尾數位和對齊位陣列的情況下，都正常地進行流水求和運算.

3) 基于現有工作中的分塊映射與片位部署的思想以及上述所提到的優化改進策略，設計完成整個模擬憶阻MVM原位運算系統.

4) 將帶優化策略的MVM原位模擬運算系統集成到高性能線性代數的算法框架中進行求解計算.評估在不同的求解精度下，系統中關鍵能耗指標的減少程度.

1 背景知識

由于憶阻器陣列存內運算具有高能效、高并行性等優勢，受到國內外學者廣泛地關注.到目前為止，用憶阻器陣列進行MVM運算的方法已經被廣泛地研究，包括從用于機器學習模型的憶阻加速器的研究到應用于科學計算的憶阻加速器的研究.

1.1 用于機器學習和圖形處理的憶阻加速器

近年來，隨著機器學習工作的流行性日益增加，學術界[12]和工業界[13]都提出了許多有關于機器學習的專用加速器的建議.這些加速器主要為機器學習模型提供MVM運算，通過加速這一過程的運算，極大程度提升機器學習模型的訓練速度.

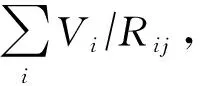
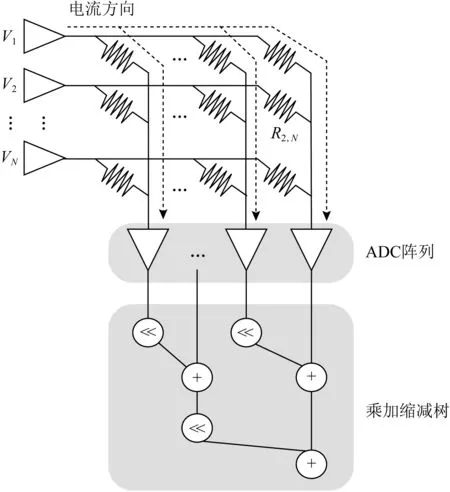
Fig. 1 Illustration of memristive crossbars computation圖1 憶阻陣列計算示意圖

Fig. 2 Array organization in a memristive cluster圖2 憶阻存儲簇中的陣列組織

2) 位切片(bit slicing)技術.由于模擬器件的精度受到非理想因素的限制，憶阻存儲單元無法精確地表達映射值[14].針對這個問題，現有的工作提出了位切片技術，這種技術通過將矩陣元素按照位片映射到多個陣列上來減少對器件精度的依賴[4-7].一個位切片的例子，這個矩陣將被映射到3個二進制存儲陣列中：

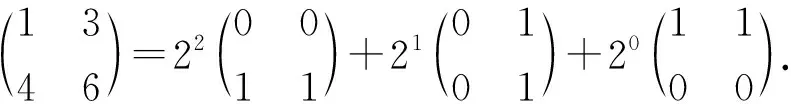
(1)

注意，在實際計算中，對于到來的電壓Vi采取這種位切片技術.

3) 乘加縮減樹.如圖1所示,為了將各位片的點積結果進行求和運算，需要乘加縮減樹進行整合[4-5]，得到MVM運算的最終結果.乘加縮減樹中有2類操作：①加法操作，即不同位片得到的結果求和；②左移操作，父結點整合左右子樹時，高位片子樹需要進行左移操作才能和低位子樹對齊相加.一般地，乘加縮減樹都是葉子結點數為2的整數次方的滿二叉樹，在這種樹結構下，整合移位時將高位子樹左移2i-1b即可(i為父結點到葉子結點的距離).

1.2 用于科學計算的憶阻加速器

1.1節提到的憶阻MVM加速器是針對機器學習模型來設計的，只提供8～16 b的計算[4-9].雖然這個運算精度大概率不會影響機器學習任務的推理準確度，但是對于高精度的科學計算求解來說，這種運算精度是遠遠不夠的[15].

1) 浮點數的憶阻陣列部署.為了解決科學計算中的精度問題，Feinberg等人[11]首次提出了在憶阻加速器上部署科學計算.在IEEE-754標準中，雙精度浮點數由53 b的二進制尾數(包括前導1)、11 b的二進制指數和一個符號位表示[16].這項工作首先提出了如何將53 b的尾數部署到憶阻陣列上進行MVM運算，它運用了多個存儲陣列，每一個陣列代表矩陣中浮點數的一個位片，形成一個存儲簇；然后再將不同的陣列通過乘加縮減樹連接起來，如圖2所示：

存儲簇用于計算向量的一個位片與矩陣元素的乘積.在完成了位片映射后，進行3階段的運算：1)電壓加載在到模塊A中的陣列上，列電流存儲在采樣—保持緩沖區中，該電流代表當前向量位片和對應的矩陣位片每一行的點積之和;2)在模塊B中，選擇器選擇采樣—保持緩沖區中代表相同行不同位片的電信號，經過ADC轉化為數字信號后，送入乘加縮減樹相加;3)模塊C中乘加縮減樹對模塊B中輸入的不同位片結果進行整合運算.

經過這3個階段，得到了矩陣的1行與向量位片的點積結果.為獲得最終結果，需要循環執行第2階段與第3階段，獲得所有矩陣行與向量位片的乘積.

2) 異構陣列集合.Feinberg等人[11]的工作還提出了一種異構矩陣分塊思想.采用不同大小的塊去捕捉稀疏矩陣中非0元素的密集區域，并為每個大小的塊設定一個非0元素閾值，若達到閾值就將該分塊映射到存儲簇上[11].對比使用單一陣列大小的工作[4-5,9]，這種異構設計極大程度上增加了陣列非0元素密度，減少了陣列映射開銷，保證了陣列的并行性和能源效率.

圖3展示了矩陣元素分塊的一種示例.其中，數據來源是SuiteSparse矩陣數據集合[2]中的685_bus矩陣.其中，圖3(a)展示了該矩陣非0元素的分布情況，圖3(b)展示了分塊之后的結果.分別采用了32×32，16×16，8×8，4×4這4種不同大小的矩陣塊對原矩陣進行分塊，閾值分別為128，32，8，2.

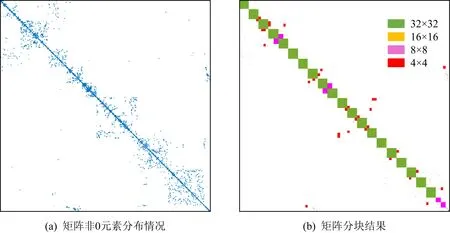
Fig. 3 Example of matrix blocking (685_bus matrix)圖3 矩陣元素分塊示例(685_bus矩陣)

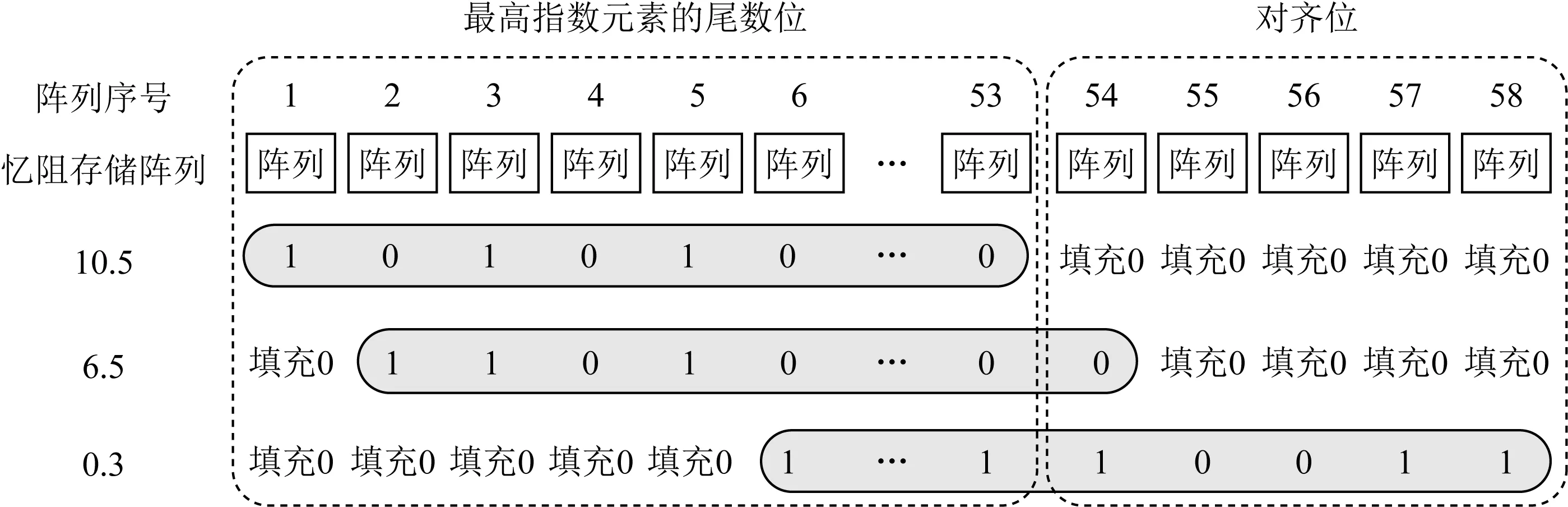
Fig. 4 Example of alignment bits deployment in cluster圖4 存儲簇中對齊位部署示例

3) 存儲簇中對齊位的部署.完成了矩陣分塊之后，需要將每一塊的浮點數都映射到存儲簇中.然而同一矩陣塊中元素的二進制指數不盡相同.為了使得不同元素的尾數按照指數對齊，需要以塊中指數最大的元素作為基準，對較小指數的元素實行向右偏移部署的策略，然后在空余位補充0.

圖4展示了存儲簇中浮點數格式部署的一個例子.需要部署10.5，6.5，0.3這3個浮點數，其對應的二進制指數分別為3，2，-2.部署時以10.5對應的指數作為基準，6.5和0.3的部署分別向右偏移1 b和5 b，并將空余位置填充0.

4) 定點硬件上執行浮點運算.在系統實現過程中，圖4所述的利用填充0實現的對齊步驟是在浮點數映射過程中實現的，該過程處于預處理階段.在陣列運算過程中，不會再出現動態的移位對齊等步驟，整個運算是在定點硬件上進行的.所以，同一個存儲簇中的陣列運算，僅涉及到定點運算.通過二進制分片策略與預處理填充對齊位的策略，實現了在定點硬件上執行浮點運算.而在整合不同存儲簇的運算結果時，會涉及到定點數轉浮點數，浮點數相加等純浮點運算.故所構造的系統是一種以定點硬件運算為主，純浮點運算為輔的系統.

2 觀察與動機

之前的工作所使用的都是固定位數的浮點數尾數部署方式，這種部署模式可能會產生額外能耗開銷.本節將討論這個問題以及對應的優化策略.

2.1 為不同的應用優化計算能耗開銷

在科學與工程領域中，雖然多數的線性模型的矩陣元素都是浮點數，但是不同應用所需的求解精度各不相同.例如，求解網頁排序算法(PageRank)、求解線性回歸等大規模數理統計模型時，所需要的求解精度都不高[17-18].已有的研究顯示，在執行機器學習、圖形處理任務時，只使用8～16 b精度就能達到令人滿意的準確率[4-9].但是，對于一些由偏微分方程離散化得到的大型稀疏性方程組而言，需要的求解精度比較高[1]，其代表領域有航天航空領域以及量子力學領域等.然而，執行高精度的求解運算必然會消耗更多的能量，這對于求解精度需求較低的線性系統來說是不劃算的.

現有工作中，高精度浮點數采用的是固定位片數的部署形式[11]，在每一個存儲簇中，有53 b的二進制尾數陣列、64 b的對齊位陣列以及9 b的校驗位陣列.在實際運算時，運算陣列與其外圍電路的能耗都與激活計算的陣列個數呈正相關，也就是說，隨著參與運算的陣列個數增多，計算能耗也會劇烈增加.然而，上述的浮點數部署模式是針對于通用IEEE-754雙精度浮點數格式設計的，對于所有的雙精度浮點應用都能夠保證計算精度.對于低精度的求解應用而言，并不需要激活所有的53 b尾數、64 b對齊位進行計算就能夠達到允許精度范圍內的解，所以按照原有固定方式計算必然會產生不必要的能耗.

2.2 尾數壓縮與對齊位優化策略

為了解決2.1節所述的為不同應用優化計算能耗開銷的問題，在本節中將論述一種尾數壓縮和對齊位優化策略，動態地決定實際運算時激活的尾數以及對齊位陣列數量.

1) 尾數壓縮策略.在實際計算時，可以根據具體的應用精度，自行選擇參與運算的尾數位數，從而大幅度減少運算陣列帶來的能量消耗.例如，如果選擇25 b尾數參與運算，在實際運算時只會激活高25 b尾數陣列進行運算，而不會對剩下的低位陣列(低28 b的陣列)施加電壓，也就不會產生這些陣列對應的運算陣列和外圍電路能耗.

2) 對齊位優化策略.在之前的有關于位片型憶阻陣列科學計算的系統設計中[11]，對齊位是固定的64 b.然而，并不是所有的應用都需要多如64 b的指數范圍.為了節省計算開銷，采取一種動態的對齊位優化策略，只部署指數范圍內的對齊位.例如，一個矩陣塊中非0元素的二進制指數范圍是1～20，即只部署19 b的對齊位陣列即可，這樣便會一定程度上減少對齊位冗余帶來的陣列計算消耗.

2.3 葉子結點數可變的流水乘加縮減樹

由于本文所提出的系統應用了尾數壓縮和對齊位優化策略，導致不同應用的計算中，尾數和對齊位的位數之和是不固定的.在這種情況下，進行計算的乘加縮減樹中葉子結點的個數是可變的.所以，為了解決尾數壓縮和對齊位優化策略帶來的葉子結點數可變的問題，需要設計一種新型乘加縮減樹結構，來完成存儲簇中不同位片結果的整合.

1)乘加縮減樹中的層級流水概念.假設目前存儲簇擁有128個憶阻陣列，陣列大小為n×n，即對應的乘加縮減樹為7層.每加載一次向量，該樹就需要計算n次，以得到矩陣塊每一行和向量相乘的結果.然而，由于樹結點之間的計算可以并行操作，且同層之間沒有數據依賴，可以把乘加縮減樹的每一層看作一個流水部件，構建一個7級的流水線.假設每個結點的計算時間為單位時間，這樣計算n個結果的時間為6+n.

2) 葉子結點數可變的流水.在以往固定位片的陣列部署模式下，葉子結點數是確定的，且數量往往是2的整數次方(若不為2的整數次方，則往往將葉子結點數補滿到2的整數次方).在此情況下，所構造的樹為滿二叉樹.現在由于葉子結點數可變，會導致整棵樹不為原有的滿二叉樹形式，導致2個問題：①由于不是滿二叉樹，各葉子結點到根結點的距離不盡相同.若采用流水策略，各葉子結點數值無法同時到達根結點，產生計算錯誤.②若所計算的乘加縮減樹不為滿二叉樹，則前面背景介紹中論述的高位子樹偏移2i-1(i為父結點到葉子結點的距離)與低位子樹對齊相加的策略就會失效，使用該方法來計算高位子樹的偏移量會帶來錯誤.為了解決這2個問題，需要提出葉子結點數可變的流水乘加縮減樹(在3.3.3節詳細論述).

3 基于異構陣列的自選尾數壓縮系統設計

本節將展示一個基于異構陣列集合，擁有尾數壓縮和對齊位優化策略，面向科學計算的MVM系統.

3.1 系統總體結構設計

如圖5所示，系統主要由預處理模塊以及陣列運算和整合模塊構成.

1) 預處理模塊.預處理部分主要負責處理原始矩陣，并提供陣列映射方案.具體地，該部分將對原始矩陣依次進行分塊、分片、執行尾數壓縮與對齊位優化策略，最終獲得能直接映射在憶阻陣列上的0-1矩陣，并為后續計算提供陣列激活策略.

2) 陣列運算和整合模塊.陣列運算和整合部分主要負責對于到來的向量x，通過陣列計算以及輔助處理子模塊的整合，獲得最終Ax的結果.具體地，需要先將向量位片按時序加載在存儲簇上，然后在陣列上執行矩陣向量乘法運算，再在輔助處理子模塊中對不同存儲簇的結果以及未分塊元素進行整合，最后得到矩陣向量的乘法結果b.

Fig. 5 Overall structure design of the system圖5 系統總體結構設計

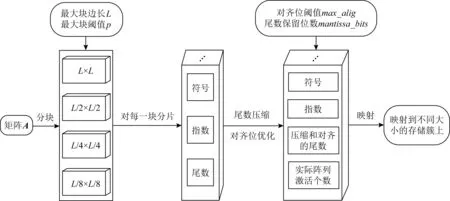
Fig. 6 Design of the pre-processing step圖6 預處理過程設計

3.2 預處理模塊的詳細設計

圖6展示了預處理模塊主要任務的設計流程：

1) 矩陣分塊與分片.由用戶輸入最大塊的邊長L和最大塊中允許的最少非0元素個數閾值p.分別運用邊長為L，L/2，L/4，L/8的塊來采集矩陣中非0元素密集的區域，其對應的非0元素閾值分別為p，p/4，p/16，p/64.在分塊過程中，先用邊長為L的塊去鋪排整個矩陣，根據閾值p去捕獲達到密度的塊，若密度達不到，則用4個邊長為L/2的塊去鋪排這個邊長為L的矩陣塊，捕獲非0元素數量超過閾值p/4的區域；以此類推，用L/4，L/8的塊去鋪排.若有非0元素沒有被任何塊捕獲，則其會進入未分塊元素集合，等待輔助處理子模塊統一整合處理.

對于每個浮點數而言，需要獲得其IEEE-754雙精度浮點數表示形式(或者其科學記數法表示形式)，進而提取其53 b尾數(包括前導1)、其指數以及其符號位.對于同一個矩陣塊，需要對其中所有的非0元素執行此操作，獲得一個具有(sign,significand,expval)三元組元素的矩陣，其中sign表示符號位；significand表示有效數，即帶前導1的共53 b尾數；expval表示對應二進制指數.

2) 尾數壓縮與對齊位優化.為實現自選尾數壓縮策略，可以在系統上增加一個尾數選擇壓縮的接口mantissa_bits，其意義是用戶設定的尾數保留位數，保留高mantissa_bits.

為實現冗余對齊位的優化，需要在矩陣分塊之后，對矩陣塊中每個非0元素的指數進行簡單處理，獲得該塊中最大的二進制指數maxexp和最小的二進制指數minexp，本系統參考矩陣塊中指數的實際范圍來進行對齊位陣列的激活.同時，本系統同時還會給出一個可供用戶設置的對齊位數閾值max_alig.對齊位數的設置形式：

alig_bits=min(maxexp-minexp,max_alig).

(2)

在一般情況下，對齊位數alig_bits=maxexp-minexp，這樣做就可以用最少的對齊位數覆蓋整個矩陣塊的指數范圍，相對于固定的對齊位方案而言減少了不必要的計算能耗.給定用戶設置的閾值max_alig的目的是為了防止在矩陣塊中有個別指數極小的元素，導致maxexp和minexp差距過大，需要用到過多的對齊位，白白耗費陣列資源.當然，如果具體的問題對求解精度要求不高但對于節省能耗的要求較高，用戶也可以根據節省能耗和求解精度的具體要求選擇較小的對齊位閾值，這一點是靈活的.

如果矩陣塊中有元素的指數超過了閾值所限制的范圍，則在預處理步驟中這些元素會重新被歸類到未分塊元素中，而不會在后續進行陣列映射.尾數壓縮和對齊位優化的過程都在預處理步驟進行，即在陣列映射前完成.可以通過這2個步驟確定每一個存儲簇中具體需要激活使用的陣列數量.

圖7展示了尾數壓縮與對齊位優化策略在預處理模塊中整體的執行流程：

Fig. 7 Design of mantissa compaction and alignment optimization圖7 尾數壓縮與對齊位優化的設計

3) 映射.對于每一個矩陣塊，需要將其映射到對應的存儲簇上.假設矩陣塊大小為N×N，一共需要映射的陣列個數為M個.則對應的存儲簇由M個N×N的憶阻存儲陣列組成，將得到的矩陣塊尾數二進制串按照從高位到低位映射到這M個存儲陣列上即可.

3.3 陣列運算與整合模塊的詳細設計

本節主要闡述，在一個已經完成映射的憶阻異構陣列集合中，從加載向量x，到計算出最后的結果Ax，這一完整過程的設計.

3.3.1 陣列運算與整合模塊結構設計

圖8展示了陣列計算和整合模塊的設計結構.其中，在每個存儲簇的輸入緩沖區中，對于到來的向量x進行分片和對齊，并以時序展開，依次輸入存儲簇中進行運算.存儲簇通過陣列點積的計算以及乘加縮減樹的計算，將向量x的當前位片值與當前矩陣塊的點積結果存在輸出緩沖中.接下來的工作由輔助處理子模塊完成，包括整合同一存儲簇不同向量位片的結果，整合不同存儲簇及未分塊元素的結果.全局緩存區用于存儲必要中間值以及最后的結果.

Fig. 8 Crossbar computation and integration module structure圖8 陣列運算與整合模塊的結構

3.3.2 負數的處理

在矩陣A和向量x中，會出現負浮點數，本節將對這2種負數的處理方式進行論述.

1) 矩陣塊中的負數處理.為了處理矩陣A映射到存儲陣列上的負數值，可以將一個矩陣塊中的正數值和負數值分開映射(以三元組中的符號位元素作為判斷標準)，然后在后續整合模塊的時候相減即可.這樣，同一存儲簇中就要維護2個陣列集合，分別對應該矩陣塊的正非0元素和負非0元素.在存儲簇c中，正存儲陣列集合和負存儲陣列集合分別為cpos和cneg.

2) 向量的負數處理.對于向量x來說，可以用負電壓來代表x中的負數元素.但是這會導致一個問題，即產生的電流值會有負數，進而經過ADC轉換之后會有負數值進入乘加縮減樹.然而本工作中實現的乘加縮減樹沒有集成關于減法(或補碼)的運算，這會導致其無法處理負數值.為處理這個問題，可以給進入乘加縮減樹的電流轉換值都增加一個數值為N的偏移，其中N為該存儲陣列的大小.這樣便能夠將電流轉換的取值范圍從-N～N轉換到0～2N.然后，由于在整合模塊中正數陣列的值要和負數陣列的值一一相減，所以增加的偏移值會在運算中剛好抵消，而不用額外操作來消除偏移值.

3.3.3 葉子結點數可變的流水乘加縮減樹的設計

如2.3節所述，相對于普通的葉子結點數固定的滿二叉樹形式，葉子結點數可變的樹形式存在2個問題：移位策略失效、流水過程計算出錯.下面將針對這2個問題提出正確的樹的結構設計.

1) 解決移位策略失效的問題

在乘加縮減樹是滿二叉樹時，假設當前結點到葉子結點的距離為i，現在該結點需要整合左右2棵子樹的元素，即將右子樹(規定右子樹為高位子樹)的值左移2i-1位，和左子樹相加即可.例如，某個葉子結點數為8的滿二叉樹，這棵樹共有3層.考慮其最高位元素，它相對于最低位的元素需要左移7 b.它在從葉子結點到達根結點前需要經歷i=1，i=2，i=3這3層中對應結點的共3次移位，總共移動21-1+22-1+23-1=1+2+4=7 b，剛好符合移位要求.對于編號為奇數的葉子結點也同理，例如第5個元素，其需要左移4 b.它在到達根結點之前需要經歷i=3層結點的1次移位(因為在i=1與i=2層中其為左子樹不需移位)，即總共移動23-1=4 b，符合要求.

現在由于應用了尾數壓縮與對齊優化策略，葉子結點的數量不會固定為2的整數次方，乘加縮減樹不再為滿二叉樹，會導致原有移位策略失效.若按照傳統方法，從根結點開始構造該1棵葉子結點為6的盡量平衡的二叉樹的話，結果如圖9(a)所示.其中，結點A的實際偏移量應為5，而按照原有偏移策略算得的偏移量為22-1+23-1=2+4=6，產生錯誤.而如圖9(b)模式構造樹，符合原有的計算模式，其偏移為21-1+23-1=1+4=5，偏移值正確.

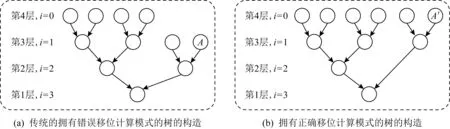
Fig. 9 Comparison of trees with wrong and correct shift computation modes圖9 擁有錯誤與正確移位計算模式的樹的對比

當前的目標是設計擁有正確移位模式的乘加縮減樹的構造策略.即需要對任意數量的葉子結點，找到一種通用策略，構造如圖9(b)所示的正確移位模式的樹.受到偏移模式以及一些從葉子結點開始構造的樹(如霍夫曼樹)的啟發，可以選擇由葉子結點開始構造這樣1棵具有正確模式的計算樹.具體地，從葉子結點層開始，兩兩相鄰的結點為一組，構造下一層父結點；若本層有落單結點(如果結點數為奇數則最后一個結點為落單結點)，則該落單結點和新構造的父結點一起組成一個新的集合，繼續構造接下來一層的父結點.如此循環地執行該構造策略，當新的集合中的結點數為1時，樹的構造停止，該結點為根結點.

如此構造乘加縮減樹，便可用i的值計算出這些結點所在的實際層數，保證每個結點在運算中能獲得正確的偏移量，到達根結點的時候獲得了正確的總移位值.圖10左圖用這種方法構造了1棵有11個葉子結點的具有正確移位計算模式的乘加縮減樹.可以看到，在i=0這一層中，結點A落單，它與i=1層的5個結點一起，構造了i=2這一層的結點，然而，在這一過程中，結點A所對應的i值不變，仍然為0.同理，對于結點B，其為i=2這一層的落單結點，它與i=3這一層的結點一起構造了i=4這一層的結點，同時，結點B對應的i值仍然不變，即i=2.

所以，對于結點A的計算過程而言，其到達根結點C需要經過結點B和結點C的移位計算，其中在結點B處移位22-1=2 b，在結點C處移位24-1=8 b，一共移位2+8=10 b，符合要求.

2) 解決無法進行流水操作的問題

想要在改進后的乘加縮減樹中執行層級流水策略，會因為各葉子結點到根結點的距離不同而導致計算錯誤.如圖10左圖所示，葉子結點D到根結點C的路徑長為4，而葉子結點A到根結點C的路徑長為2.由于每進行一次流水操作都要對葉子結點加載一批新的數值，所以，當結點A經過2次流水操作到達結點C時，同一時刻輸入的結點D值還沒到達結點C；當結點D值到達結點C時，此時從結點A到達結點C的值已經是2個周期之后加載在結點A的值.所以，在計算過程中始終面臨著數據達到不同步的錯誤.

① 結點維護先進先出隊列.為了解決無法流水的問題，可以讓每一個結點都維護一個先進先出隊列，用隊列的長度來彌補某些葉子結點到根結點的距離比其他葉子結點短的問題.圖10右圖展示了圖10左圖中乘加縮減樹對應的隊列結構.可以發現，由于結點A，B，C這一計算路徑長度為2，這個值要小于滿二叉樹部分的計算路徑(例如從結點D經歷3個中間結點到結點C，其路徑長為4)，所以需要結點A和結點C的隊列長度為2，其余結點的隊列長度為1.當父結點需要整合左右子樹的值時，只需要從左右子樹取出其隊首的值進行操作即可，在圖10右圖中實線代表該子樹需要移位后才能進入父結點進行相加操作，虛線代表可以直接進入父結點進行加法操作.具體地，若當前需要計算的父結點的取值隊列為cur，左右子樹的取值隊列分別為left和right，則計算整合的過程描述為

cur.push(left.pop+right.pop?2i-1).

(3)

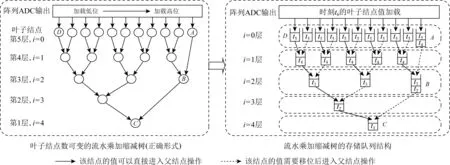
Fig. 10 Example of the correct pipelined multiply-and-add tree圖10 正確形式的流水乘加縮減樹的結構示例

圖10右圖描述了第6次向樹的葉子結點中加載數值時，樹各結點中隊列的存儲情況.其中，ti代表該結點隊列中存儲值在數據流中的時間順序，例如t4代表該值是由第4次加載在葉子結點中的數據流經過乘加縮減樹對應位置計算得到的值.可以看到，在結點A和結點C中分別需要存儲t4，t5和t2，t3的值，以保證在i=2層計算時，結點B要從結點A中獲得t4時間順序的值，且保證在i=4層計算時，結點C要從結點B中獲得t2時間順序的值.

Fig. 11 Auxiliary processing module workflow圖11 輔助處理子模塊工作流程

② 維護正確的隊列長度與存儲值.現在設計的關鍵是要讓所有葉子結點的計算路徑上都存儲相應長度的隊列，這樣層級流水才能取得正確的值.由此，在流水線沒有充滿的時候，不能夠一次性地激活所有流水層級，而是一級一級地激活.以圖10為例，第1次加載數據時，需要激活層i=0計算；第2次加載數據時，激活層i=1，即此時i=0和i=1這2層參與計算，直到最后第5次加載數據時，激活流水所有層級計算；并且在隨后的計算中，都是每一次加載數據，然后流水的所有層級一起計算.這樣一來，在激活i=1的時候，只有i=0和i=1這2個層級在計算，結點A按照順序儲存了2個待加值；同理，在激活層i=2和層i=3后，結點B按順序儲存了結果，符合預期.

3.3.4 輔助處理子模塊的運算設計

圖11展示了該過程中輔助處理子模塊的處理步驟與全局緩沖區中的內容變化：

經過了陣列運算與乘加縮減樹整合之后，每個存儲簇的緩沖輸出中都儲存了矩陣塊與向量位片的乘積結果，下面稱這個結果為關于該向量位片的部分和.

輔助處理子模塊將對這些結果進行整合，獲得最后的Ax結果.具體解釋：

1) 設該存儲簇c存儲的矩陣為Ac，其中正數與負數存儲陣列集合為cpos和cneg，向量第j位片對應的部分和為Ac×xj.將不同位片的部分和相加，得到當前矩陣塊正數元素以及負數元素陣列與向量x的乘積結果bcpos與bcneg.

4) 將未分塊元素列表unblock_list中的元素都整合到向量b的中間結果中，得到b的最終結果.

4 基于異構陣列的自選尾數壓縮系統實現

本工作將用軟件模擬實現所設計的憶阻MVM系統.具體地，將用Python程序模擬實現硬件的存儲結構、運算框架的構造以及數據在系統中的計算.本節將對系統中關鍵的存儲結構、系統處理流程的具體實現作出詳細的介紹.

4.1 硬件結構的實現

本系統需要模擬的硬件主要包含憶阻運算陣列(存儲簇)以及乘加縮減樹結點.本系統將用Python的類(class)中的成員變量來模擬各個存儲結構所包含的存儲項，若在運算過程中需要請求使用硬件資源，則只需要用軟件編程方法實例化對應的類即可.具體地，本系統存儲結構需要實現3種類.首先是有關陣列的2個類，分別是單個憶阻陣列和相同大小憶阻陣列組成的存儲簇，表1展示了其模擬存儲結構(類中需要儲存的成員)；其次是乘加縮減樹結點硬件所對應的類，表2展示了其模擬存儲結構.

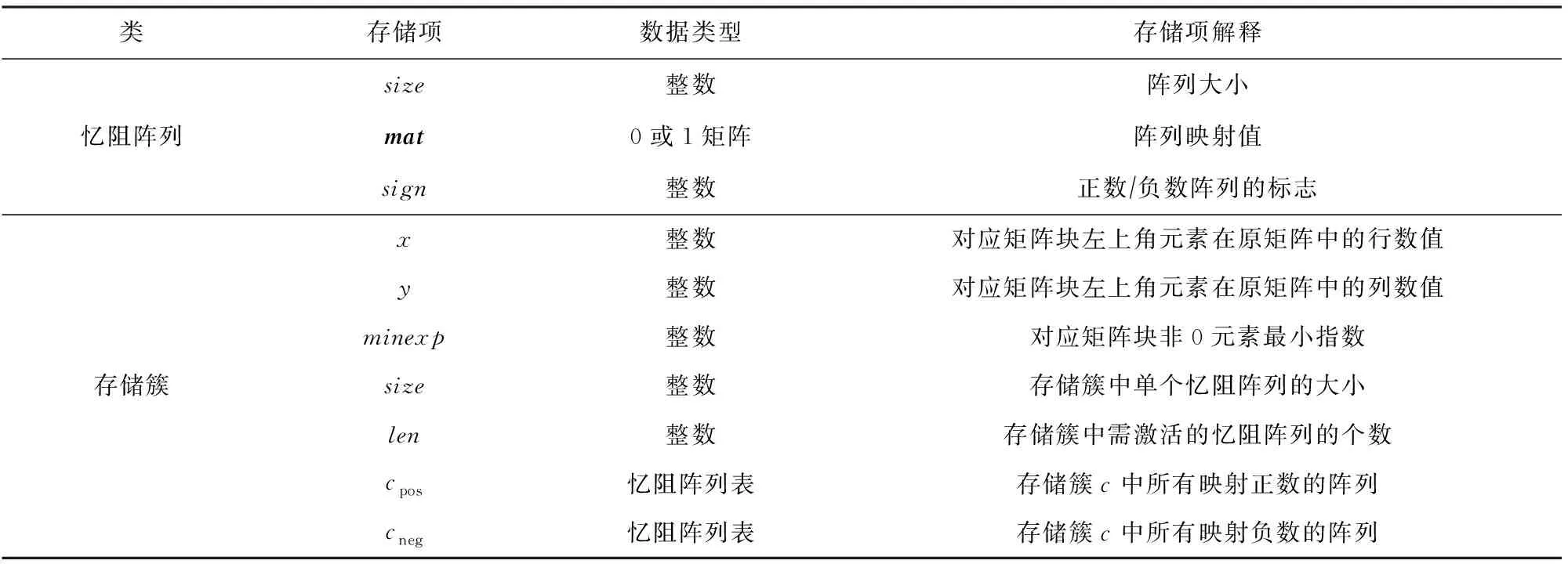
Table 1 Data Storage Structure of a Storage Cluster and a Single Memristive Crossbar

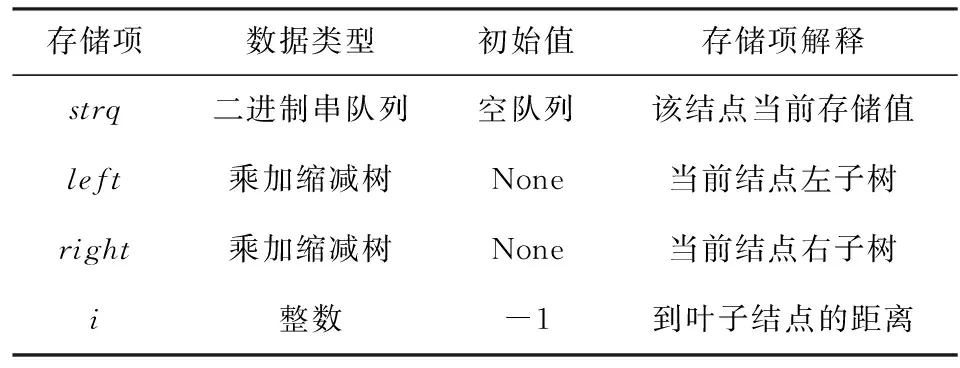
Table 2 Storage Structure of Nodes in Multiply-and-Add Trees

4.2 系統處理流程的實現

在實現了模擬憶阻存儲結構的基礎上，可以對憶阻陣列進行映射與計算.下面將介紹整個系統處理過程的實現要點.

4.2.1 整體實現流程

本節將從總體角度介紹如何用程序模擬數據在憶阻系統中的計算.圖12顯示了整個系統的實現流程，下面將對照該圖論述數據在系統中的計算以及系統的總體實現結構.

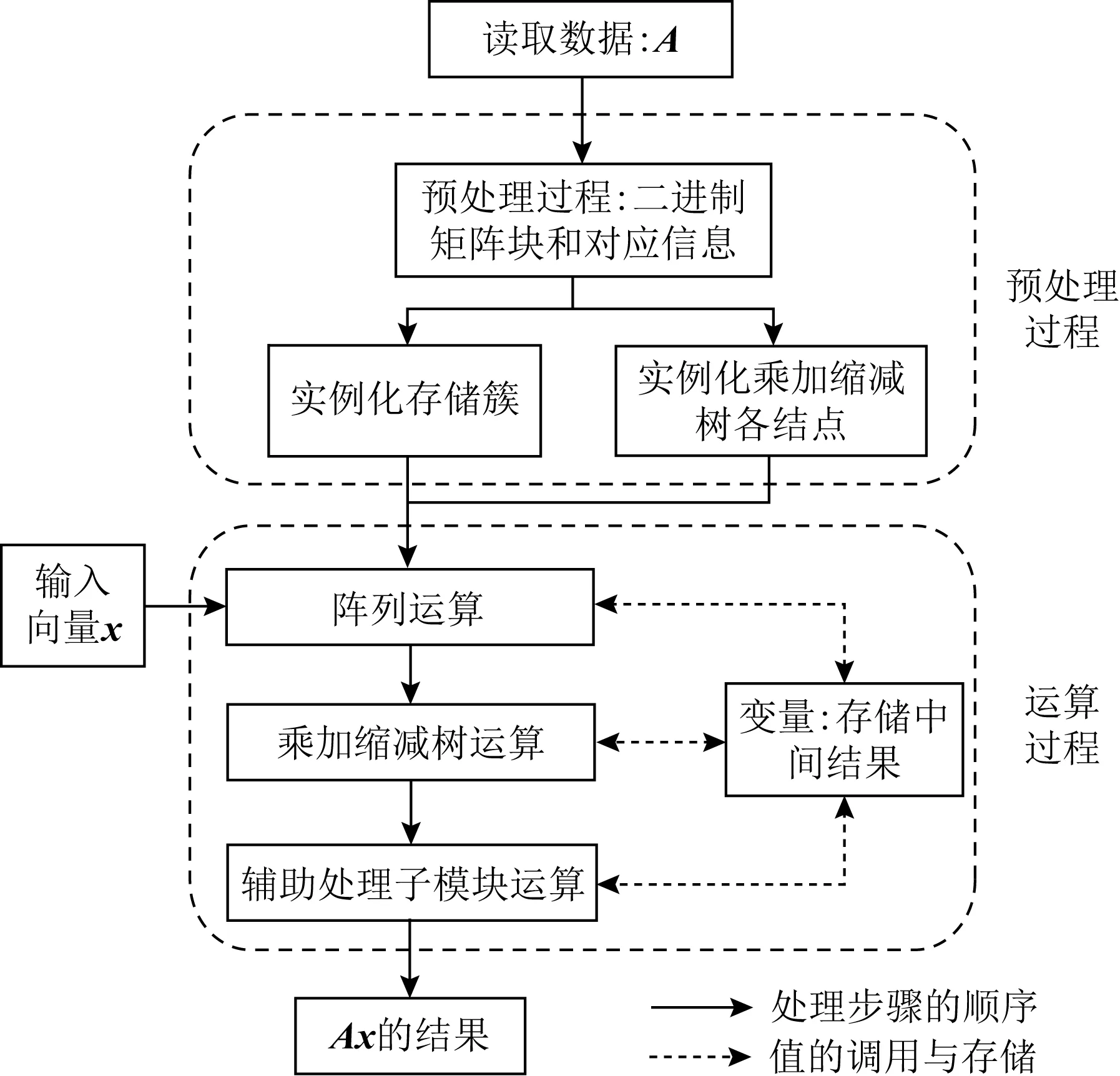
Fig. 12 Overall system implementation process圖12 系統整體實現流程

首先，從文件中讀取原始矩陣A(具體地，用Python的scipy.io庫讀取原始“.mat”文件，具體數據信息在5.1.2節中介紹).然后，進入預處理過程，該過程得到了經過尾數壓縮與對齊位優化后的異構二進制矩陣塊，以及各矩陣塊對應的信息.對每一個矩陣塊，都實例化對應的存儲簇和乘加縮減樹結點的Python類，以達到用軟件方法模擬實現硬件資源的目的.預處理過程(包括分塊分片、尾數壓縮和對齊位優化過程)都用Python源代碼實現，封裝成一個Python程序模塊，預處理具體數據時調用該模塊即可.最后進入運算過程，分為3個步驟：1)陣列運算，將向量x與憶阻陣列中0-1矩陣進行點乘，運算結果存儲在對應變量中(用變量模擬圖8所示的緩沖輸出).2)進行乘加縮減樹運算，按照3.3.3節中的描述，編程實現每一個結點的移位和加法操作，同時維護結點正常的隊列長度，保證數據流在樹結構中的正常路徑.3)輔助處理子模塊中運算的過程.主要包括部分和的求和、定點數轉浮點數、不同存儲簇結果與未分塊元素的整合，用變量來模擬圖8中的全局緩存區.用Python源程序實現整個運算過程，封裝成一個模塊，接收已完成數據映射的憶阻存儲結構以及輸入向量x，返回矩陣向量乘法的結果.

4.2.2 預處理過程與陣列運算的實現

預處理過程主要包括分塊、分片、尾數壓縮和對齊位優化、矩陣映射4個步驟，完成了映射之后，便可以加載向量元素進行陣列運算.

1) 分塊信息表block_list和未分塊信息表unblock_list的構造與維護.在矩陣分塊過程中，按照塊由大到小循環遍歷整個矩陣，這個過程中需要記錄分塊元素信息，存在block_list中.表中元素為元組(x,y,size)，分別代表該分塊的左上角在原矩陣中的行數值、列數值以及塊的大小.如果遍歷到最小塊仍然滿足不了分塊閾值要求，或者遍歷完整個矩陣后有沒有處理到的邊角元素時，需要記錄其中的非0元素(即未分塊元素)，存在unblock_list中.該表中元素為元組(x,y,val)，分別代表該元素在原矩陣中的行數值、列數值以及對應的浮點數值.

2) 矩陣塊處理映射過程.當block_list構造完成之后，便可以進行相應處理將每個矩陣塊映射到對應的存儲簇上.首先，根據(x,y,size)提取當前需要處理的映射塊A′=A[x:x+size,y:y+size].對該矩陣塊A′進行分片、尾數壓縮與對齊位優化，獲得一個提供最終映射信息的矩陣A″，其矩陣元素為(符號位，壓縮與對齊后的有效數二進制串，指數)三元組.通過這個信息矩陣不難將矩陣塊按位片映射在表1所示的存儲簇結構上，存儲關鍵數據信息.需注意，處理過程中要根據“符號位”的數值為1或0，選擇將其映射在負數陣列集合還是正數陣列集合中.

3) 陣列運算.完成映射后，需要根據當前存儲簇結構存儲的y和size值，提取需要相乘的向量片段x′=x[y:y+size].然后，對x′進行分片與對齊，按照位片從高到低加時序地載到存儲簇的電壓端.對于每一次向量位片的加載，經過流水乘加縮減樹的運算整合，輸出其與矩陣塊的乘積，即該向量位片對應的部分和.

4.2.3 部分和求和的實現

1) 部分和求和計算.每加載一次x位片，乘加縮減數就輸出一次部分和.在此，采用動態策略進行部分和的求和運算，即每產生1次部分和，就進行1次加法運算，每一次求和計算：

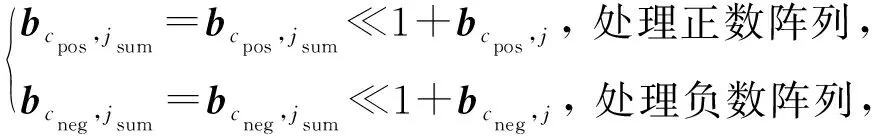
(4)

其中，cpos(cneg)為當前進行部分和求和的存儲簇c對應的正數(負數)陣列集合，j代表加載第j個x位片，向量b則為該系統最后需要求得的結果，即Ax的結果.bcpos,j(bcneg,j)則代表當前存儲簇中正數(負數)陣列集合在第j個x位片的作用下得到的部分和結果；bcpos,jsum(bcneg,jsum)代表前j個部分和結果相加得到的最終結果.

2) 部分和求和的提前終止策略.在上述過程中，隨著輸入的x位片指數降低，其在結果中的權值降低.事實上，在后續二進制轉浮點的操作中，結果中多余的低位片數值將會被截斷.本工作利用文獻[11]提到的方法，應用部分和求和提前終止策略，設定結果最多保留位數為m(一般m=53)，則當結果bcpos,jsum(bcneg,jsum)的高m位穩定不變時，求和過程結束.記結束時，當前存儲簇c中cpos和cneg對應的部分和求和結果是bcpos和bcneg.

求和終止需要滿足3個條件：1)后續求和區域與高m位沒有重疊.2)高m位后面出現一個值為0的阻隔位，用于吸收后續求和元素產生的進位.3)值為0的阻隔位出現之后，需要再計算1次，若阻隔位沒有變成1，則求和才能終止.這一步是為了避免阻隔位翻轉讓后續計算向高m位產生進位.部分和求和終止時的形式如圖13所示：

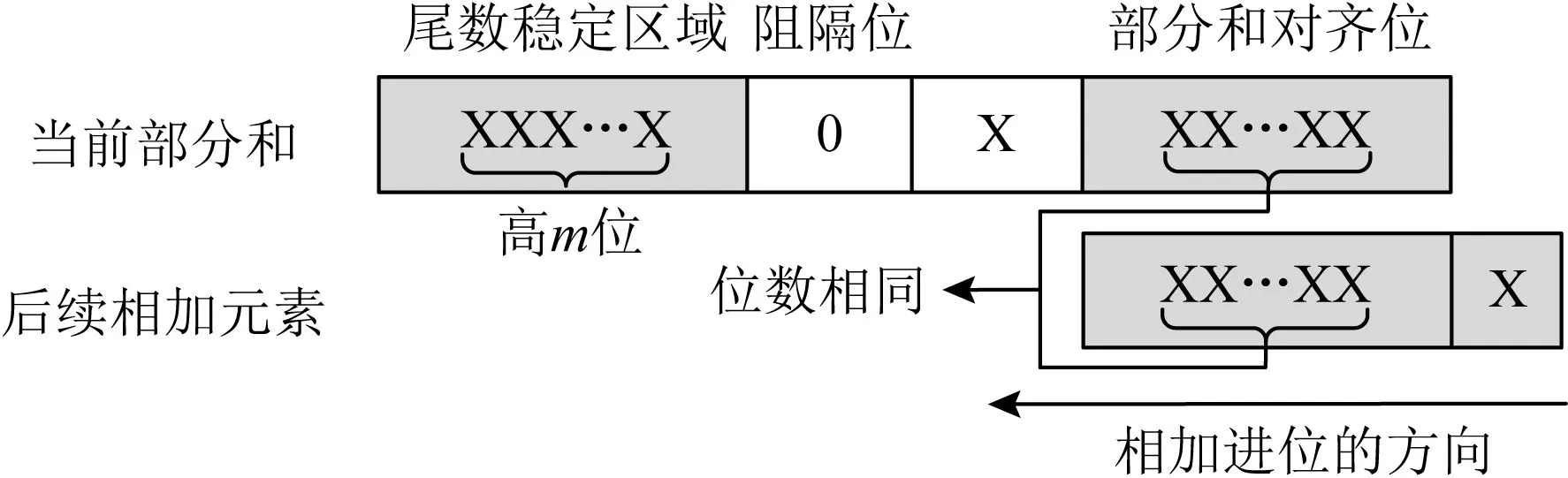
Fig. 13 Partial sum early termination strategy圖13 部分和求和提前終止策略

4.2.4 定點數轉浮點數

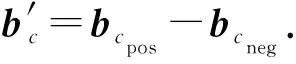
expvalc=len_c+min_x+min_c-mantissa_bits,

(5)

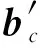
4.2.5 不同存儲簇結果與未分塊元素的整合

4.2.2～4.2.4節所述的陣列計算、部分和的求和計算，均是針對同一個存儲簇中的運算而言的.要獲得Ax的結果，需要將不同的存儲簇中的結果整合起來.在這一過程中，需要全局地維護結果向量b.

1) 不同存儲簇結果的整合.遍歷所有的存儲簇進行運算，都會產生對應的MVM運算結果bc，對所有存儲簇c整合到b中：

b[i+c.x]=b[i+c.x]+bc[i],
i=0,1,…,c.size-1.

(6)

2) 未分塊元素整合.計算的最后一步是將unblock_list中的元素整合到結果向量b中，對于unblock_list中的第i個元素(xi,yi,vali)進行計算(假設unblock_list的長度為len_u)：

b[xi]=b[xi]+x[yi] ×vali,
i=0,1,…,len_u-1.

(7)

4.3 預處理部分開銷分析

整個系統的開銷主要包括預處理開銷與運算開銷.其中，運算開銷主要包括模擬電路開銷(以運算陣列開銷為主)與數字電路開銷(以ADC轉換開銷為主).運算開銷的評估與分析將在第5節作詳細討論，本節主要對預處理部分的關鍵開銷進行定性分析與評估.

預處理部分的主要開銷來自于原始矩陣分塊開銷、確定塊內指數范圍開銷、構造葉子結點數可變的乘加縮減樹開銷這3個方面.其中，后2個開銷是原系統[11]中沒有涉及到的，即是由于應用了尾數壓縮和對齊位優化策略，系統在預處理部分多出的開銷.

1) 原始矩陣分塊開銷.假設一個矩陣中非0元素的個數為Nnz，按照本文提出的算法，將用4種不同大小的塊對原矩陣的非0元素密集部分進行捕捉，每個元素最多遍歷4次，即在最壞情況下需要進行4×Nnz次操作.已有的工作發現，在平均情況下，對于原始矩陣分塊的開銷大約為1.8×Nnz次操作[11].

2) 確定塊內指數范圍開銷.為確定實際需要激活的運算對齊位個數，需求得每個矩陣塊元素中最大指數和最小指數的差值，這就要遍歷矩陣塊中所有非0元素.由于矩陣塊捕捉的都是原始矩陣中非0元素的密集區域，假設原矩陣中非0元素密度為K，邊長為l，則這一步驟總開銷(對整個原始矩陣)與Kl2成比例.

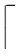
4.4 實現上的限制分析

本系統在實現時會遇到一些限制，本節將從硬件物理實現和實際測試負載應用2個角度討論.

1) 硬件物理實現.本文所提出系統的實現與評估都是通過編寫軟件程序模擬仿真實現的.這是由于目前的憶阻陣列制備工藝尚不成熟，不能夠支持如此大規模、擁有多陣列尺寸大小的憶阻系統的物理實現.但使用軟件實現的模擬系統在評估測試中也有其獨特的優勢，可以靈活調節軟件參數來改變分塊大小、壓縮位數等重要參數，快速得到各種情況下的理論結果.

2) 實際測試負載應用.尚未找到一種方法，能對所有的測試負載都找到效果可觀的尾數壓縮和對齊位優化方案.實際應用該系統時，可能會由于部分參數選擇不當(如尾數壓縮位數、對齊位閾值)，達不到需要的優化效果或精度要求.

5 評估與分析

本節將在線性代數求解框架中集成所實現的系統，對不同求解精度下的各種能耗節省比例進行評估.

5.1 評測數據與評估方法

下面將對模擬MVM內核集成到算法框架中的方法、評估所用的數據以及評估方式作詳細論述.

5.1.1 MVM內核的集成方法

1) 算法求解框架.常用的高性能線性代數迭代求解算法有共軛梯度法(conjugate gradient method, CG)[19]、雙共軛梯度穩定法(biconjugate gradient stabilized method, BICGSTAB)[20].在本課題中，將使用Python的scipy.sparse.linalg庫中已經實現的CG/BICGSTAB算法框架來進行測試評估.這種算法框架支持以線性運算符(linear operator)的形式將模擬MVM內核應用于迭代求解，算法框架(以CG為例)：

(8)

在輸出端元素中，x為線性系統的解，flag為收斂標志(0代表收斂).在輸入端參數中，A代表原始矩陣或者線性運算符，b代表線性方程組的右手向量，x0代表解向量的初始值，默認為零向量；tol代表解的容差，即|b-Ax|

2) 運用線性運算符集成MVM內核.在式(8)中，輸入參數A可以是線性運算符，其作用是包裝一個函數，函數輸入為x，返回Ax的結果給算法求解框架.Python的scipy.sparse.linalg庫提供線性運算符的包裝方案，其框架：

A=LinearOperator(A.shape,matvec,rmatvec),

(9)

其中，matvec和rmatvec是2個關鍵函數，它們的輸入都是x，返回分別為Ax和ATx.為實現MVM內核的集成，需編寫這2個函數，在函數體中調用實現的MVM模擬系統，通過輸入的向量x和固定的矩陣A，計算得到對應的Ax或ATx，作為函數的返回.

3) 預條件子的使用.在式(8)中，輸入參數M代表預條件子矩陣.預條件子是在解決大型稀疏矩陣求解問題時的一種常用優化手段[21-22].關于預條件子矩陣，通俗的解釋就是需要找到一個和稀疏矩陣A相似的矩陣M，對于對原等式Ax=b作出M-1Ax=M-1b的變換.其中M-1A和M-1b都可以直接算出，而且由于M和A為相似的矩陣，所以M-1A的值接近于單位矩陣，極大程度上減少了求解的步數.有一種通用的預條件子方法為0級不完全LU分解(incomplete LU factorization with level-0 fill in, ILU(0))，該方法利用單位下三角矩陣L和上三角矩陣U構造M=LU，使得M接近于A，并在矩陣中執行0級填充，保持矩陣原有的稀疏模式.在Python的scipy.sparse.linalg庫中，有spilu這樣一個求解類，可以用于構造ILU(0)預條件子，并集成到算法框架中.在后續測試中，存內硬件求解器都將集成ILU(0)預條件子.

5.1.2 評測數據集

評測將采用SuiteSparse矩陣集合[2]中的矩陣作為數據集.SuiteSparse矩陣集合是科學與工程領域中的實際應用產生的稀疏矩陣集合，該集合被廣泛地用于稀疏矩陣算法的開發和性能評估.

根據需要，選用了大小不一的6個稀疏矩陣，作為評測數據.其中，部分數據文件只給出了矩陣A的值但是沒有給出右手向量b的值.對于這部分數據，在進行CG/BICGSTAB算法求解時參照文獻[21]的做法，構造全是1的右手向量b進行測試.表3顯示了6個矩陣的名稱、矩陣行數(rows)、非0元素數量(Nnz)、平均每行非0元素個數(Nnz/rows)等基本信息.

為了后續評估不同求解精度下的能量消耗比例，需要一些有關于憶阻器件的參數來輔助進行能耗評定.表4列舉出了一些真實的憶阻器件參數[9,23].

Table 3 Evaluated Matrices Dataset表3 評測矩陣數據集

Table 4 Memristive Device Parameters表4 憶阻器件參數

5.1.3 評估方法

在下面的評估中，主要考慮只進行對齊位優化、尾數保留35 b、尾數保留25 b、尾數保留15 b這4種優化策略(3種尾數保留策略也是在對齊位優化的基礎上進行).在憶阻MVM運算中，這4種策略所激活的陣列個數依次減少，會導致求解精度下降，但是會獲得極大的能耗節約.

為了評估所設計的自選尾數壓縮機制和動態對齊位優化機制的有效性和效果，將在CG和BICGSTAB這2種算法下評估4種策略的3個指標：1)相對于軟件求解基線的相對殘差及對應的迭代次數.2)運算陣列能耗相對于能耗基線的優化程度.3)ADC能耗相對于能耗基線的優化程度.其中，能耗基線指在原系統[11]對應的條件下(尾數53 b、對齊位64 b固定不變)測得的對應種類的能耗(在本文的測試中，對齊位閾值也選擇為64 b).

通過評估這3個指標，可以分析出隨著激活運算陣列的減少，計算精度的下降(通過計算對于軟件求解基線的相對殘差來體現求解的精確程度)，運算陣列和ADC能耗的優化程度.驗證所提出的系統是否可以在為高精度應用提出無損浮點計算功能的同時，又能有效降低較低精度應用的能耗開銷，以體現系統實現方案的有效性和良好效果.

5.2 不同策略下的求解精度與迭代次數

由于只進行對齊位優化的情況下并不會影響MVM的計算精度，即此策略下的解向量與迭代次數與軟件求解完全一致，所以不再對其進行單獨測定.本節主要關注5.1節提到的3種尾數壓縮策略.

5.2.1 評估標準

用殘差來描述不同策略下求解精度相對于軟件求解基線的差距，求解殘差：

(10)

5.2.2 評估結果與分析

本節展示在各種尾數壓縮策略下，求解結果相對于軟件基線的相對殘差以及算法求解的迭代次數.

1) 各種尾數壓縮策略下解的相對殘差.圖14分別顯示了在BICGSTAB(圖14(a))、CG(圖14(b))測試算法下，3種尾數壓縮策略相對于軟件基準的相對殘差.總體來說，在對6個數據集測試結果進行對數平均處理后，3種策略的相對殘差分別在10-9，10-7，10-3這一數量級.具體地，對于同一種尾數壓縮策略，2種算法解向量的相對殘差是幾乎相同的，可以認為壓縮策略影響的是映射矩陣本身的性質，不會因為算法框架的改變而發生太大的結果變化.對于每一種算法的每個測試矩陣而言，隨著保留位數的減少，相對殘差都會成數量級地增大.

2) 各種尾數壓縮策略下算法的迭代次數.圖15顯示了在2種測試算法下各策略對應的算法迭代次數.總體來說，進行適當范圍內的尾數壓縮不會對迭代次數產生大的影響.但是，如果壓縮的位數太多，保留位數太少，可能會增大迭代次數(如圖15中保留15 b尾數時的測試矩陣msc00726的測試結果).為了進一步驗證該想法，分別繼續測試了測試矩陣msc00726在只保留15 b，12 b，9 b，6 b這4種尾數位情況下2種算法的迭代次數.結果顯示，BISGTAB算法的迭代次數對應分別為2，2，3，5，CG算法的迭代次數對應分別為3，3，4，9.可以看出，如果尾數保留位數過少，會顯著增加求解迭代次數，使得迭代求解過程需要更多的時間和能耗.故在實際應用中，需要謹慎選擇尾數壓縮位數，盡量不選擇過少的保留位數(如15 b以下)，以防止尾數壓縮策略給求解帶來的負面影響.

Fig. 15 Algorithm iteration times under various compaction strategies圖15 各種壓縮策略下的算法迭代次數

5.3 不同優化策略下的運算陣列能耗評估

運算陣列能耗是模擬電路中最大的能耗來源.進行陣列運算時，電壓加載到電阻上，會產生瞬時功率.為了使得采樣—保持數組能夠獲得正確的電流值，通常需要使得電流維持一段時間，所以會產生能量消耗.本節將展示在4種優化策略下，運算陣列能耗相對于能耗基線的減少比例.能耗基線的值是在已有未優化系統[11]的條件下評估得到的，其尾數為固定的53 b，對齊位為固定的64 b.

5.3.1 評估指標

參數如表4所示，每一個存儲單元的瞬時功率：

(11)

采樣—保持數組需要電流維持的時間主要取決于其RC時間常數，它與分辨率，即lbN是成比例的，其中N是當前憶阻存儲陣列的大小(行數)，即一個存儲單元的計算能耗與P×lbN是成比例的[11].

為了獲得進行一次Ax運算所對應的運算陣列能耗Ecrossbar，需要依次進行3個具體步驟計算：

1) 對于加載1次電壓(1個向量位片)而言，需要對所有陣列中的所有存儲單元的能耗值進行求和，得到憶阻存儲結構的整體能耗;

2) 對于每一次向量位片的加載，將上述整體能耗進行累加，得到Ecrossbar;

3) 為了求解迭代過程中的運算陣列總能耗，需要對所有Ax步驟的Ecrossbar求和，得到一個與迭代陣列消耗總能量成比例的值Ecrossbar_tol.

5.3.2 評估結果與分析

評估求解過程中，各策略Ecrossbar_tol的相對比例.

Fig. 16 Computation crossbar energy ratio under various strategies圖16 各種策略下的運算陣列能耗比例

1) 各種壓縮/優化策略下的運算陣列能耗比例.以測試矩陣mesh3em5在BICGSTAB算法下的測試得到的Ecrossbar_tol為單位能量，畫出在2種算法下，所有矩陣在各種策略下的能耗值，如圖16所示.首先，對于同一個算法同一個測試矩陣而言，隨著每個存儲簇中激活運算的陣列越來越少(從只進行對齊位優化，到尾數保留位數分別只有35 b，25 b，15 b)，運算陣列消耗的能量也逐漸變少，符合預期.同時，可以觀察到，矩陣中非0元素越多，消耗的陣列能量明顯越多.這是因為其非0元素多，導致其映射電阻中Ron較多，導致能耗較大.并且注意到，消耗的運算陣列能量與原始矩陣大小沒有直接關系，比如在6個測試集中，最大的矩陣(行數最多的)為測試矩陣Chem97ZtZ，但是其中的非0元素沒有測試矩陣bcsstk27多，所以消耗能量明顯比測試矩陣bcsstk27小很多.對于同一個測試矩陣而言，由于CG算法的迭代次數多于BICGSTAB，所以消耗的運算陣列能量也成比例的增加.

2) 各種壓縮/優化策略下的運算陣列平均能耗優化.表5展示了對于所有6個測試矩陣平均值而言，使用每一種策略時運算陣列能耗相對于能耗基線減少的比例.可以發現，BICGSTAB和CG這2種方法的能量優化比例是幾乎相同的，并且隨著運算時激活陣列的減少，能耗優化比例會越來越大.具體地，在相對于軟件方法有0～10-3范圍的求解殘差時，2種算法下的平均運算陣列能耗都相對已有的未優化系統減少了5%～65%.

Table 5 Average Computation Crossbar Energy Optimization Ratio

5.4 不同優化策略下的ADC能耗評估

ADC是將采集-保持數組中的電信號轉化為數字信號的部件，只有經過這種轉換，乘加縮減樹才能對陣列中的計算結果求和.ADC能耗是外圍數字電路能耗的主要來源.本節中將展示4種優化策略下的ADC的能耗相對于能耗基線(已有未優化系統[11]條件下評估得到)的減少.

5.4.1 評估指標

假設一個陣列的大小是N，則其所需要的ADC分辨率為lbN.因為ADC的平均功耗隨分辨率呈指數增長[24-26]，故其功耗和N成比例.又因為ADC的轉換時間與分辨率lbN成正比，所以列電流的轉換能耗與N×lbN成正比[11].

假設某個存儲簇中有M個存儲陣列.即對于每一個存儲簇，每一個單獨的向量x位片要進行M×N次列電流的計算，則存儲簇進行一次計算ADC的總能耗與M×N×N×lbN成正比.

為了獲得一次Ax的完整ADC能耗EADC.需要在算法執行過程中對所有存儲簇，所有的向量x位片的ADC能量求和，得到最終EADC.注意EADC的值只是與真實的ADC能耗成比例，而非真實ADC能耗值，其只會被用來計算相對于能耗基線的能量節省比例.

最后，為了計算求解迭代過程中的ADC總能耗，需要對所有Ax計算產生的EADC求和，得到求解整個算法ADC消耗的總能量值EADC_tol，該值與迭代求解過程中真實的ADC能量消耗成比例.

5.4.2 評估結果與分析

評估求解過程中，各策略下EADC_tol的相對比例.

1) 各種壓縮/優化策略下的ADC能耗比例.以測試矩陣mesh3em5在BICGSTAB算法下的測試得到的EADC_tol為單位能量，畫出所有矩陣在各種算法、各種執行策略下的能耗比例.圖17顯示出一些與運算陣列能耗優化(圖16)相同的性質.比如，矩陣塊的非0元素越多，ADC的能耗明顯越多，因為需要更多的陣列進行運算，對應的ADC轉換過程也就越多.再比如由于CG算法的迭代次數明顯比BICGSTAB算法要多，所以其ADC能耗也成比例的多.

對同一個算法同一個測試矩陣而言，隨著每個存儲簇中激活運算的陣列越來越少，ADC能耗基本上也逐漸變少，符合預期.但是需要注意，對于測試矩陣msc00726和測試矩陣nos5而言，應用對齊位優化策略相對于能耗基線并沒有一個明顯的ADC能耗下降，這是因為其矩陣塊內指數范圍太大，超過了設定的閾值64，對齊位優化效果不明顯.

對于大多數矩陣而言，ADC能耗隨著保留的尾數位數的減少而降低.但是對于測試矩陣msc00726而言，在保留15 b尾數的時候，其ADC能耗反常地比保留25 b時要多，這是由于尾數截斷過多使得算法迭代的次數增加，導致要用到更多計算步驟來使得算法收斂.所以須注意，由于壓縮位數過多導致迭代次數增加，最終導致計算能耗過多的情況也會發生，對于ADC能耗來說可能更明顯，需要謹慎選擇壓縮位數.

Fig. 17 ADC energy ratio under various strategies圖17 各種策略下的ADC能耗比例

2) 各種壓縮/優化策略下的ADC平均能耗優化.表6展示了對于所有6個測試矩陣平均值而言，每種執行策略的ADC能耗相對于能耗基線減少的比例.和運算陣列能耗一樣，各種策略在應用于BICGSTAB和CG這2種算法的情況下，對ADC能耗減少的比例幾乎是一致的，且隨著運算激活陣列數的減少，能量優化比例逐漸增大.具體地，在相對于軟件方法有0～10-3范圍的求解殘差時，2種算法下的平均ADC能耗都相對于已有的未優化系統減少了30%～55%.

Table 6 Average ADC Energy Consumption Optimization Ratio

與運算陣列能耗優化的情況不同的是，ADC能耗在只應用對齊位優化時，其能耗優化程度約為30%，它大于同樣策略下的運算陣列優化的數值(約5%).但是，隨著存儲簇中陣列激活數量(保留尾數位數)的逐漸減少，ADC能量優化的效果沒有運算陣列能量明顯.運算陣列的能耗在保留15 b的時候優化比例在65%左右，而ADC能耗在尾數保留位數15 b時優化比例只有55%左右.

6 結束語

在科學與工程領域中，浮點數線性系統的求解問題十分普遍.現有的研究提出將IEEE-754雙精度浮點數部署在憶阻陣列上，進行高能效的存內計算.然而，還沒有研究提出為不同求解精度的浮點線性系統優化運算能耗.為解決這個問題，本文創新性地提出了一種具有尾數壓縮與對齊位優化策略的浮點MVM計算系統，并針對該策略的特征提出了一種葉子結點數可變的流水乘加縮減樹.評估結果表明：本系統既可進行高精度浮點數無損運算，又可對低精度求解應用大幅度優化運算陣列與ADC的能耗.

作者貢獻聲明：丁文隆提出了本文工作的思路，設計完成了實驗，并撰寫論文；汪承寧協助改進系統框架，在論文寫作過程中提供理論基礎的幫助；童薇對整個工作提出指導意見并修改論文.