基于ARIMA 模型的民航旅客運輸量預測
李黎莎
(中國民用航空飛行學院民航監察員培訓學院,四川 廣漢 618307)
民航旅客運輸量是反應我國航空公司、機場運行效率的重要指標,同時也反應了我國旅客出行的需求情況和先關企業經營管理水平,科學準確地對旅客運輸量進行預測和分析能有利于對航空公司、機場等民航運行單位的保障能力配備及運力投放提供決策支持。目前,對交通運輸領域的預測主要集中在公里、鐵路等交通量、短時交通流、票價方面。童名榮等[1]在ARIMA 的基礎上通過對比分析,推導出預測精度更高的具有周期的季節性ARI-MA 模型;李萬等[2]將相關性分析得到的鐵路營業里程、國家鐵路客車擁有量、國內生產總值和年末總人口作為鐵路客運量的影響因素并對鐵路客運量進行預測,提出改進粒子群算法(IPSO)和將粒子群算法(PSO)與長短時記憶神經網絡相結合的預測模型。在民航領域中也對航班延誤量、機場運輸量、空管保障架次、平臺旅客訂票需求等多方面進行了預測研究。丁松濱等[3]采用SARIMA-LSTM 模型對民航各類飛行保障架次的時間序列進行預測,驗證了此預測模型對民航空管系統各單位保障架次有較好的預測效果;蔡文婷等[4]通過對民航運輸客運量歷史數據對所構建多元回歸模型的預測值進行比較分析,驗證了多元回歸模型的預測值與歷史數據的相對誤差較小、預測精度較高。本文利用民航局2007 年1 月至2019 年6 月的連續序列建立了基于ARIMA 的預測模型,留用2019 年下半年運輸量數據用于驗證模型的準確性,并對民航旅客運輸量進行分析預測。
1 民航旅客運輸量概況
根據中國民用航空局月度旅客運輸量統計數據[4],歷年民航旅客運輸量(2007.1-2019.12)。以年為x 軸,對應的月度旅客運輸量為y 軸,單位為萬人次,繪制時序圖,如圖1。
由圖1 可知,2007-2019 年旅客運輸量總體呈上升趨勢,從2007 年1 月的月度旅客運輸量1241.7 萬人次,2019 年12 月達到5276 萬人次,是初始數據月的4.25 倍。對比民航行業的建設發展情況:2007 年,北京首都機場擴建,民航運輸機場數量為152 個,在冊航空器1134 架。2019 年,北京大興機場投入使用,民用運輸機場數量達到238 個,是2007 年的1.57 倍;民航全行業運輸飛機期末在冊航空器3818 架,比上年底增加179架,是2007 年的3.36 倍。民航旅客運輸量主要受我國國民經濟發展水平、居民收入水平、機場建設水平及服務能力等方面因素的影響。從以上數據可以看出,旅客運輸量的增速和民航行業建設發展情況一致。故對民航旅客運輸量數據的預測和分析有助于把握民航發展趨勢,為各民航單位合理安排新增運力、完善運行戰略規劃等具有重要指導意義。

圖1 2007-2021 年民航旅客運輸量時序圖
根據時序圖的規律性變化還可以看出,年度內旅客運輸量保持有規律的季節性波動,年變化趨勢基本呈現相同規律。民航旅客運輸量在每年2 月和7-8 月受春運、暑運影響,處于一年中運量最大值;在春運、暑運后出行人次顯著降低。
2 ARIMA 模型介紹
2.1 ARIMA 模型
差分自回歸平移模型(Autoregressive Integrated Moving Average, ARIMA)模型是一種有效的時間序列預測模型,是20 世紀60 年代有美國學者Box 和英國學者Jenkins 提出的。如使用ARIMA 模型分析的時間序列具有趨勢,則對其作差分后變為平穩隨機序列,再用平穩時間序列去建立描述這一隨機過程的模型。最后,運用最佳擬合的模型,過去、現在的時間序列觀測值對未來數據進行預測[1]。ARIMA(p,d,q)中,自回歸模型AR,p 為自回歸項數;移動平均模型MA 為滑動平均,q 為滑動平均項數,d 為使之成為平穩序列所做的差分次數,即階數。ARIMA(p,d,q)的模型為

式中:y(t)為時間t 的旅客運輸量;λ(B)為自回歸算子;d 為差分次數;B 為延遲算子;θ(B)=1-θ1B-θ2B2-,…,θqBq 為移動平滑系數多項式(q 為移動平均階數);εt為零均值白噪聲序列。
2.2 數據來源
本文以2007-2019 年旅客運輸量為基礎數據序列,數據來源于中國民用航空局年度民航行業發展統計公報和月度運輸生產指標統計[4]。
2.3 建立模型
采用SPSS 統計分析軟件, 建立了ARIMA預測模型,原始序列為連續139 個月的民航旅客運輸量,以萬人次為單位。由圖2 原始序列的自相關(ACF)圖可知原始序列是非平穩的,根據圖3 原始序列偏自相關(PACF)圖可知需對原始旅客運輸量序列進行差分,將原始序列進行預處理使其變為平穩的時間序列,見圖4-5。

圖2 原始序列自相關圖

圖3 原始序列偏自相關圖

圖4 差分序列自相關圖

圖5 差分序列偏自相關圖
對于ARIMA 模型,若自相關函數在滯后數為p 后截尾和偏相關函數在滯后數為q 后截尾,則階數分別為p 和q。利用SPSS 反復計算嘗試后,基于最小信息量(AIC)原則,選擇ARIMA(3,1,3)作為原始序列的最優模型,即p=3,d=1,q=3,其模型的其他參數如表1 所示。
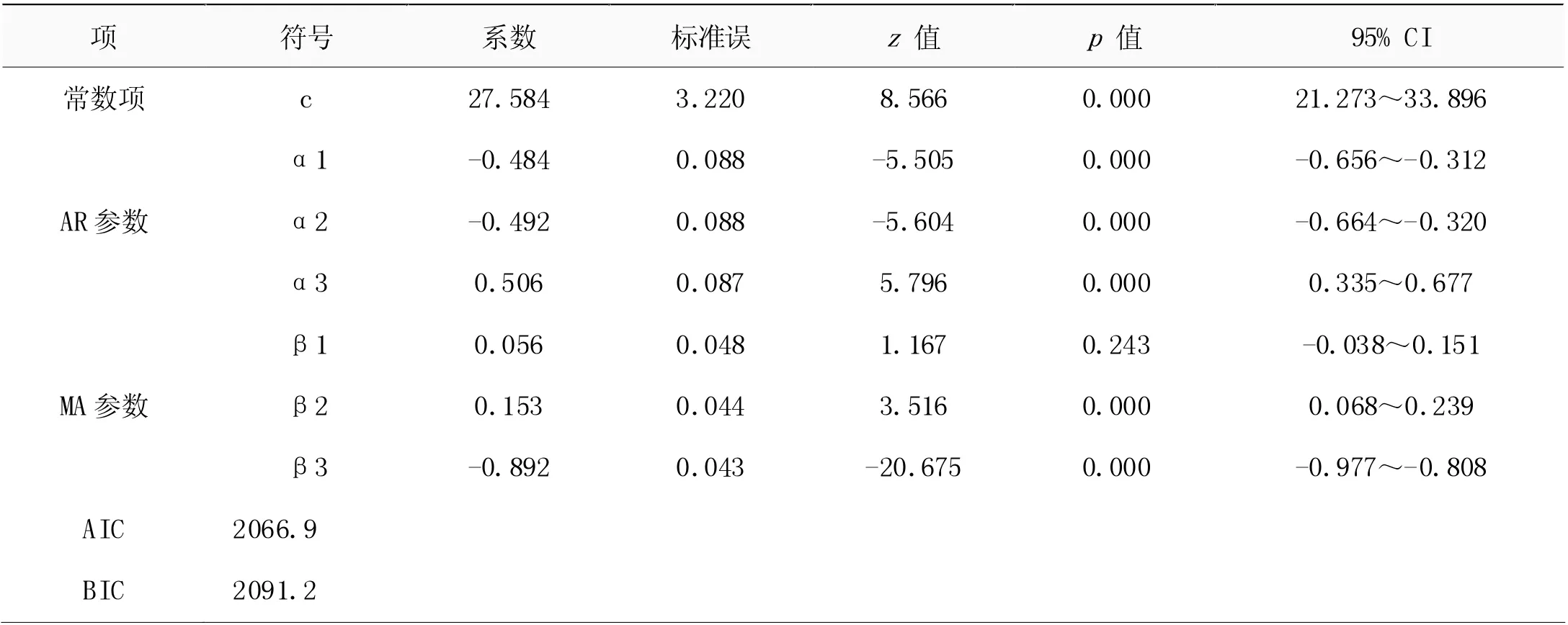
表1 旅客運輸量預測ARIMA(3,1,3)模型參數表
模型在殘差檢驗中P=0.614>0.05,滿足殘差的白噪聲檢驗,不存在殘差的自相關性,驗證了該預測模型是可靠的,見表2。所以,可得出最優ARIMA 模型公式為:

表2 模型Q 統計量表格

2.4 旅客運輸量預測與驗證
使用該模型進行旅客運輸量預測,圖6 為該最優預測模型ARIMA (3,1,3) 的擬合值與2007-2019 年真實數據的對比,由圖可見該模型擬合良好。
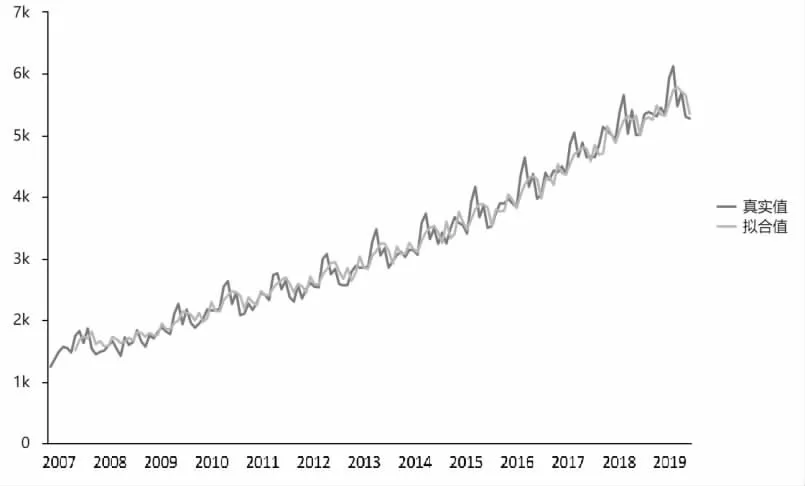
圖6 2007-2019 年旅客運輸量擬合
使用2019 年8 月-12 月的實際旅客運輸量數據對該預測模型進行驗證,誤差值分別為1.22%、0.85%、0.92%、1.37%、1.36%,如表3。較小的預測誤差值表明該模型的預測結果準確、預測精度較好,可用于后續民航旅客運輸量的分析研究。在利用模型對2020 年12 個月的旅客運輸量進行預測數據,結果如表4。由2020 年的預測結果可見,最大旅客運輸量仍出現在元旦、春節及暑假期間,在節后呈現下降趨勢,其波動情況與歷史數據一致。

表3 2019 年8-12 月旅客運輸量預測值與真實值的誤差分析
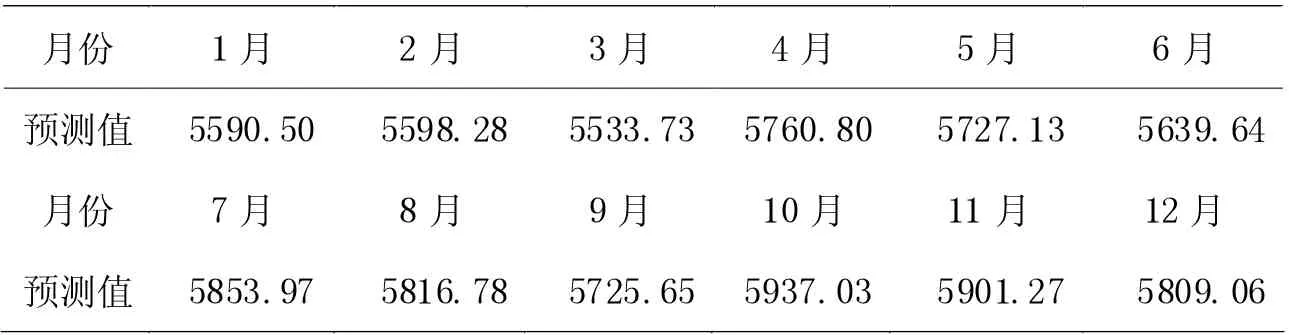
表4 2020 年旅客運輸量預測
3 結論
本文選取了2007 年1 月至2019 年7 月連續139 個月的民航旅客運輸量數據進行預測,建立了基于ARIMA 模型的旅客運輸量預測模型,并使用2019 年8-12 月的真實數據進行驗證,預測結果準確,說明了使用該模型進行建模預報是可靠的。但是,該模型未考慮突發事件對民航行業的擾動,在公共衛生事件、自然災害、金融危機等情況下,該模型存在一定的局限性。在不考慮疫情的影響下,該模型能在民航正常運行的情況下較為準確地預測出旅客運輸量,可供航空公司、機場等民航運行部門在資源保障和運力部署等方面提供決策支持。

