基于改進禁忌搜索算法求解TSP 問題
唐文秀
(華北電力大學,北京 102206)
1 概述
在數學領域中,TSP 問題(Traveling Salesman Problem,即旅行商問題),被廣泛視作一個典型的組合優化問題[1]。該問題一般講述的是為一個旅行商尋找最短路徑,該商人計劃在n 個不同的城市為產品作宣傳,并且每個城市只能經過一次,從初始城市出發,遍歷所有目的城市且不重復后,又回到初始城市。顯然,該問題屬于組合優化問題,在生活中非常普遍,很多實際工程應用問題的實質就是旅行商問題,例如某旗艦店的商品物流路線、物資分配、車輛調度、電路布線、產品生產安排問題等等[2-4]。因此,研究TSP 問題不僅具有重大的實際意義,也具有相當高的工程價值。
當城市數量較少時,理論上可以通過窮舉法來列舉出最優方案,然而當城市數量較多時,所有路線之和將呈指數增加,因此求解過程非常復雜而且很難找到最優解。目前,求解TSP 問題的算法大致可劃分為兩類,分別是確定性算法和智能優化算法[5]。確定性算法通常是指能利用數學公式解出具體的某個數值,且該結果即為最優解,例如線性規劃、動態規劃、完全枚舉等方法,然而該類算法只適用于小規模算例求解,因此,考慮到現實應用情況,在規模較大時,人們常常選擇目前廣受關注的智能優化算法,例如遺傳算法、粒子群算法、模擬退火算法、禁忌搜索算法、免疫算法以及人工神經網絡[6-9]等等。本文主要通過遺傳算法和禁忌搜索算法兩種算法進行混合求解,結合兩種算法的優勢,對TSP 問題進行優化求解,提高解的質量。
2 改進禁忌搜索算法
1986 年,Fred Glover 教授提出了禁忌搜索算法(Tabu Search,簡稱TS 算法)[10],指出該算法的局部搜索能力非常強,并且也能避免算法陷入局部最優,從而找到全局最優解,是一種全局迭代尋優算法。多年來,該算法也以其靈活的記憶特性和特赦準則,受到了眾多學者的青睞。
所謂禁忌,是指禁止重復操作,類似于模擬人的思維模式,如果該區域已經搜索過,則下次搜索時可以通過禁忌表來進行記錄,避免重復低效搜索,但也并非完全隔絕,對于更優的解,也可以通過特赦準則對其進行釋放,改善解的質量,避免遺漏。
在TS 算法中,關鍵的參數主要有禁忌表、禁忌長度、特赦準則、候選集、適配值函數、終止準則等。禁忌表是算法的核心所在,用來記錄已經搜索過的地方,避免在搜索中陷入循環和局部最優。禁忌長度是指放置在禁忌表中的對象的禁忌周期,每進行一次迭代,周期就減少一次,直到周期為0 時即可解除禁忌。特赦準則是指在迭代過程中,出現了比歷史最優還要更優的解,盡管此時該解對應的對象處于禁忌表中,且禁忌長度不為0,也可以將其特赦出來,解禁該禁忌對象。候選集主要從領域解中產生,可以隨機選擇幾個領域解作為候選解,或者選擇表現較好的作為候選解。適配值函數是指對當前搜索過程的評價,在TSP 問題中為總的行程距離大小。終止準則指算法的結束條件,通常設置為算法執行到某一個迭代次數,或者目標函數值小于某個誤差。
TS 算法的主要搜索步驟如下所示:
(1)初始化禁忌表、禁忌長度,隨機產生初始解,定義領域映射模式;
(2)判斷初始解是否滿足終止條件,若滿足,則輸出最優解,結束搜索;若不滿足,則繼續下一步;
(3)根據當前解的領域映射模式生成若干個鄰域解,并從中選出若干候選解,計算適配值,保留較好的候選解進行下一步判斷;
(4)判斷候選解是否滿足特赦準則,若滿足,則將其特赦出來,并作為當前最優解,同時將對應的對象放入禁忌表,并修改表中各個對象的周期長度;若不滿足,則選出在候選解中沒有被禁忌的最優解作為當前最優解,對禁忌表進行重復前一步操作;
(5)當滿足終止準則時,例如迭代次數已達到最大,此時結束搜索,輸出最短路線。流程如圖1 所示。

圖1 禁忌搜索算法流程圖
雖然TS 算法具備著強大的局部搜索能力和記憶功能,但是也存在一些不足,例如,該算法對初始解具有很大的依賴性,即當初始解較好時,能夠迅速找到最優解,當初始解不好時,則直接制約了禁忌搜索的速度,因此,為了克服該問題,本文提出結合遺傳算法進行改進,首先利用遺傳算法產生較好的初始解之后,再把該解作為禁忌搜索算法的初始解來進行迭代尋優,而非隨機產生初始解。
遺傳算法的主要步驟為:第一步進行初始化操作,計算每條路線的適應度值及路徑長度;第二步,以概率的方式來選擇新的路線方案;第三步,對選擇的路線進行交叉操作,隨機交叉某兩座城市的坐標,確保每個城市有且僅經過一次;第四步,進行變異操作,即隨機交換某一條路線的一對城市坐標,得到新的路線,然后再進行下一次迭代尋優;最后判斷是否滿足終止條件,若滿足則結束搜索,輸出最優路徑及最短距離,若不滿足,則繼續進行迭代尋優。遺傳算法流程圖如圖2 所示。

圖2 遺傳算法流程圖
3 算例仿真
3.1 改進前結果
假設城市規模N=31,每座城市坐標如表1 所示。設置禁忌長度L=22,候選解的個數M=200,求出任意兩個城市的間隔矩陣,定義領域映射模式為2-opt,開始禁忌搜索操作,直到滿足終止條件。
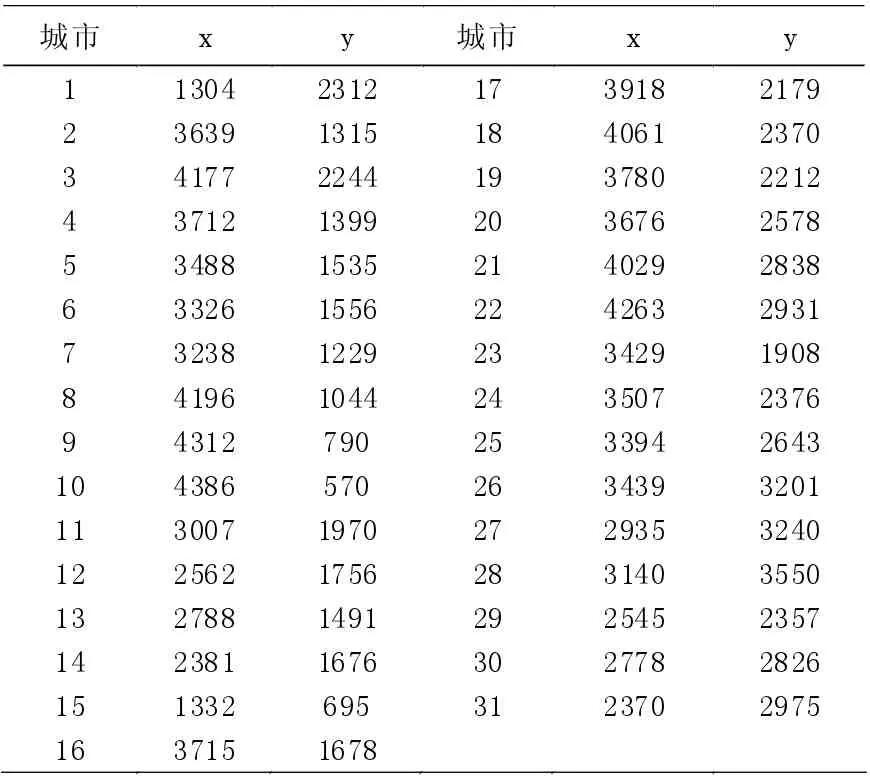
表1 31 座城市的坐標

圖3 31 座城市分布
在該問題中,分別設置迭代次數為100、300、500、800 和1000,在不同的迭代次數下,重復運行5 次程序,得到的結果如表2 所示。
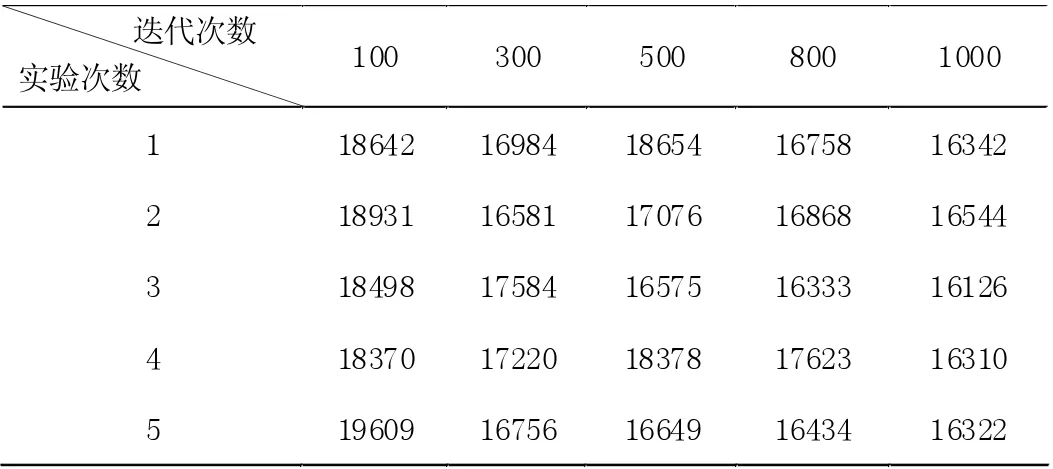
表2 不同迭代次數的實驗結果
從仿真結果可以看到,當迭代次數逐漸增大時,計算的結果逐漸減小,并逐漸趨于優化最短距離,在該案例中,當未加入遺傳算法進行改進時,在迭代次數為1000 時,優化最短距離為16126,最優路徑和適應度進化曲線如圖4、5 所示。

圖4 改進前優化最短距離
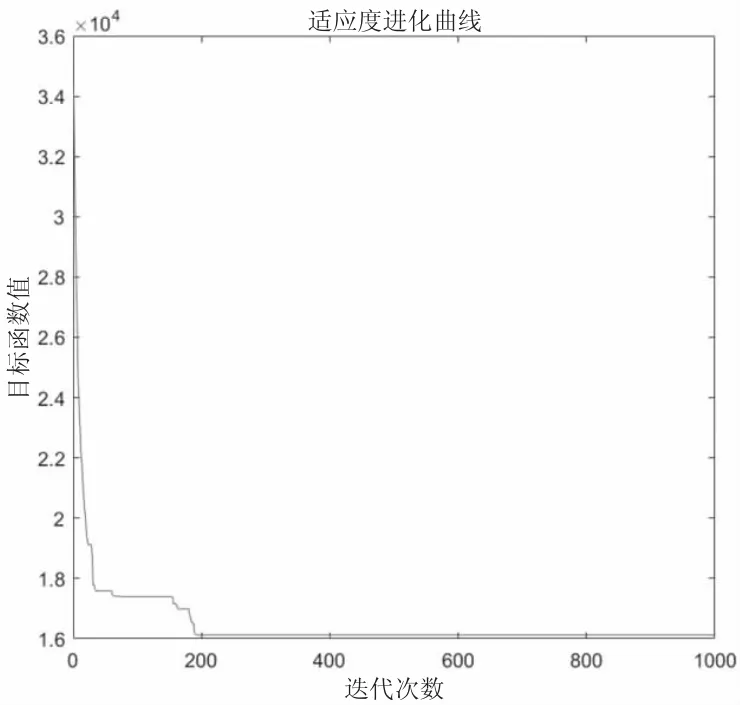
圖5 改進前適應度進化曲線
3.2 改進后結果
先通過遺傳算法進行求解,設置群體數量NP=200,染色體基因維數N=31,最大進化迭代次數G=1000,產生初始種群,計算每個個體的適應度值和最短距離,再通過選擇、交叉、變異操作進行下一次遺傳,直到迭代次數達到最大值,將此時得到的最短路線方案作為初值傳給禁忌搜索算法。在實驗中,分別設置迭代次數為100、500 和1000,在不同的迭代次數下,重復運行5 次程序,得到的結果如表3 所示。

表3 改進后結果
在加入遺傳算法后,可以看到,結果得到了極大的改善。當迭代次數為1000 時,此時遺傳算法已經越來越接近最優值,再結合禁忌搜索算法進行尋優時,可以看到改進后的結果明顯優于改進前的結果,此時得到的最短距離為15382,相比于改進前,縮短了744,路線方案如圖6 所示,適應度進化曲線如圖7 所示,藍色的線條表示僅采用禁忌搜索算法求解的結果,紅色的線條表示結合遺傳算法進行改進后的結果,可以看出,改進后的適應度值明顯低于改進前的值,說明了算法的有效性。

圖6 改進后優化最短距離

圖7 適應度進化曲線對比
4 結論
本文簡要闡述了禁忌搜索算法的基本思想、求解步驟以及實現過程等,基于MATLAB 編程了改進前的禁忌搜索算法和改進后的禁忌搜索算法,并對比了兩種方式對TSP 問題的求解的結果,實驗結果表明,改進前的禁忌搜索算法能夠找到相對最優解,但需要較大的迭代次數,且初始解較差時,求解速度緩慢,結果不夠穩定。通過遺傳算法進行改進后,結果有了較大的提高,從實驗數據可以看出,在改進前,當迭代次數為1000 時,優化最短距離為16126,改進以后,優化最短距離為15382,縮短了總的行程距離,得到了更優的路線方案,實驗結果得到了明顯的改善,算法有效并且可行。

