類Piccolo 結構的差分安全性評估

王念平，殷勍

（1.信息工程大學密碼工程學院，河南 鄭州 450004；2.航天工程大學，北京 101416）

0 引言

分組密碼作為現代密碼學的重要組成部分，在信息安全領域有著廣泛的應用。分組密碼具有易于標準化、便于軟硬件實現和容易同步等優點[1-2]，但也有一定的缺陷。例如，分組密碼不能隱蔽數據模式，即相同的密文蘊含著相同的明文組，這是因為分組密碼使用的是一個不隨時間變化的固定變換。同時，分組密碼不能抵抗組的重放、嵌入和刪除等攻擊。但上述的缺陷可以通過在加密過程中引入少量記憶加以克服，例如，可以通過密碼分組鏈接（CBC,cipher block chaining）方式來克服[2-3]。另外，分組密碼的安全性很難被證明。盡管“可證明安全性”的研究發展很快，但目前的分組密碼大多是“看起來安全”的，還沒有哪一個著名的分組密碼真正被證明是安全的，至多證明了局部安全性。

對于分組密碼，目前還存在一些問題值得考慮。一是分組密碼算法的標準化。分組密碼的大量社會化應用呼喚密碼算法的標準化。二是分組密碼設計和分析理論的研究。作為分組密碼的研究者，總是希望從理論上解釋一些設計方法的合理性，并將一些分析方法理論化，而不僅僅是停留在設計經驗和直觀分析的層次上。例如在一定假設條件下的可證明安全性和偽隨機性常常是研究者追求的一個目標。三是分組密碼安全性分析的自動化。這是計算機技術與密碼分析的有機結合。將一些密碼分析方法程序化，往往可以提升分析的深度，彌補手工分析的不足。四是分組密碼算法評估的實用化。算法的評估不僅要考慮在傳統數學模型下的安全性，還應結合實現和應用環境評估算法的安全性，例如在側信道模型下的安全性。本文的研究屬于第二項內容。事實上，分組密碼的整體結構對分組密碼的安全性有很大影響。因此，研究分組密碼結構的安全性一直是分組密碼研究領域的重要內容。

差分密碼分析[4]是一種典型的分組密碼分析方法。差分密碼分析能否成功主要取決于所利用的差分特征概率的大小。文獻[5]指出，在最大差分特征概率足夠小的情況下，就認為該密碼算法對差分密碼分析是免疫的。但在現實中，計算最大差分特征概率有一定的困難，且較難實現，所以就退而求其次——計算最大差分特征概率的上界，而最大差分特征概率的上界的計算取決于活動輪函數或活動S盒個數的下界。需要指出的是，在計算差分特征的活動輪函數或活動S 盒個數的下界時，一般并不考慮輪函數和S 盒的具體細化結構，而只是假設它們是雙射的即可，從而所得的結果更具普遍性。文獻[6-9]就是基于這樣的思路進行分析的。

Piccolo 結構[10-11]是從Piccolo 算法[12]中歸結出來的一種密碼結構，如圖1 所示。其設計特點在于塊移位變換RP 不直接對4 個分塊Y0、Y1、Y2、Y3進行移位，而是對平均分成的8 個子分塊進行移位。文獻[10]研究了Piccolo結構抵抗差分密碼分析的能力，證明了k(k≥ 1)輪差分特征至少有k-1個活動輪函數和(n+1)(k-1)個活動S 盒（n+1是輪函數中P 變換的差分分支數）。文獻[11]改進了文獻[10]中的結果，證明了k(k≥ 6)輪差分特征至少有k個活動輪函數和(n+1)k個活動S 盒，并指出活動輪函數個數的下界結果是不可改進的，所謂不可改進，是指確實存在一類差分特征，其活動輪函數的個數恰好達到了給出的下界。本文在此基礎上，提出32 種類Piccolo 結構（包括文獻[10-11]中的Piccolo 結構），并對這些類Piccolo 結構進行了差分密碼分析，給出了活動輪函數和活動S 盒個數的一個下界。

圖1 Piccolo 結構

本文的結果與文獻[10-11]相比，改進之處在于文獻[10-11]只是針對Piccolo 結構這一種密碼結構進行分析的，而本文是針對提出的32 種類Piccolo結構進行分析的。本文的結果比文獻[10]中的結果要好，比文獻[11]中的結果更具一般性。

1 預備知識

1.1 基本概念

定義1[13]設(X,+)和(Y,+)都是有限交換群，f:X→Y,α∈X,β∈Y，差分概率p f(α→β)定義為

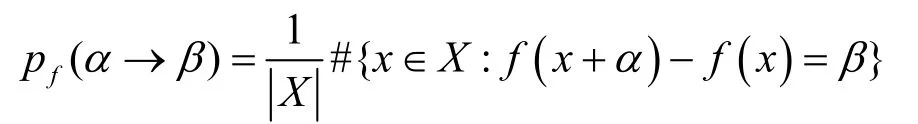
其中，“| · |”和“#{·} ”表示集合的基數。

定義2[1]r(r≥ 1)輪差分特征Ω是一個差分序列α0,α1,…,α r，其中α0是明文對Y0和的差分，αi(1≤i≤r)是第i輪輸出Yi和的差分。

定義3[14]輸入差分非零的輪函數（S 盒），稱為活動輪函數（S 盒）。

定義4r(r≥1) 輪差分特征中活動輪函數的個數稱為該差分特征的活動指標。

本文稱r(r≥1) 輪差分特征的活動指標為r(r≥1) 輪Piccolo 結構的活動指標。本文中，將n元塊移位變換簡記為 (i0i1···in-1)，它表示按從左到右的順序將原來第ij個分塊aij移動到第j(j=0,1,…,n-1)個分塊的位置，即

1.2 類Piccolo 結構描述

圖2 類Piccolo 結構

表1 集合A

表1 中，8 元塊移位變換 (i0i1···i7)表示移位變換（下同）。

1) 輪函數f0,1f

如圖3 所示，輪函數f0,1f都采用SPS 結構，這里S 表示n個m×m雙射S 盒（n為偶數且nm=t，t為輸入塊X i(i=0,1,2,3)的比特數），P 表示的線性變換x→Mx，M表示有限域GF(2m) 上的n階MDS 矩陣。易知，P 變換的分支數（包括差分分支數和線性分支數[13]）為(n+1)，且輪函數f0,1f都是雙射。

圖3 輪函數

2) 塊移位變換σ

集合A中的8 元塊移位變換是滿足以下2 個條件的置換。

條件1ij∈{2,3,6,7},j=0,1,4,5；ik∈{0,1,4,5},k=2,3,6,7。

形象地說，滿足條件1的σ如圖4 所示，即i j(j=0,1,4,5)只能從 {2,3,6,7} 中選取，ik(k=2,3,6,7)只能從{0,1,4,5}中選取。

圖4 滿足條件1的σ

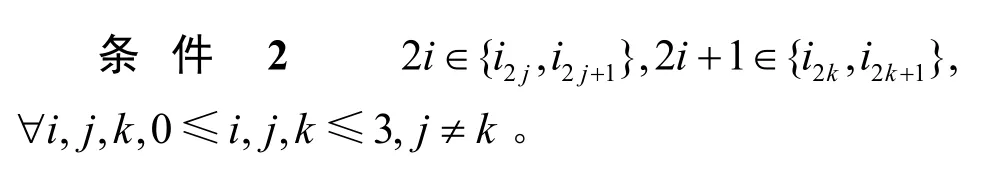
形象地說，滿足條件2的σ如圖5 所示，即將每個大塊2i2i+1 中的2 個小塊2i和2i+1 分別移位到不同的大塊中去。

圖5 滿足條件2的σ

條件1 和條件2 共同保證了類Piccolo 結構的擴散效果。

備注1為了敘述方便，將塊移位變換是σ的類Piccolo 結構稱為σ-Piccolo 結構。

2 類Piccolo 結構的活動輪函數和活動S 盒個數的下界

為了分析方便，將X i(i=0,1,2,3)看成由左右規模相等的兩部分x2i和x2i+1連接而成，即X0=x0||x1,X1=x2||x3,X2=x4||x5,X3=x6||x7，其中“||”表示比特塊的連接。那么，類Piccolo 結構的輸入就可表示為(x0||x1,x2||x3,x4||x5,，一輪類Piccolo 結構（略去子密鑰）的輸入和輸出關系式就可表示為

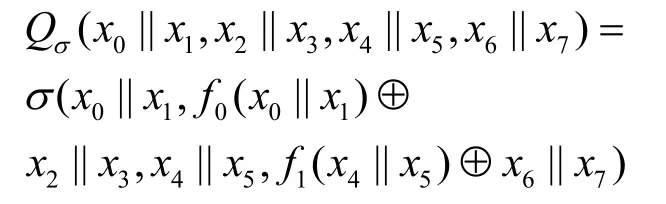
首先，給出σ-Piccolo 結構的差分對應的結構形式。

定理1對任一σ-Piccolo 結構，設具有非零概率的一輪差分對應都具有如下形式

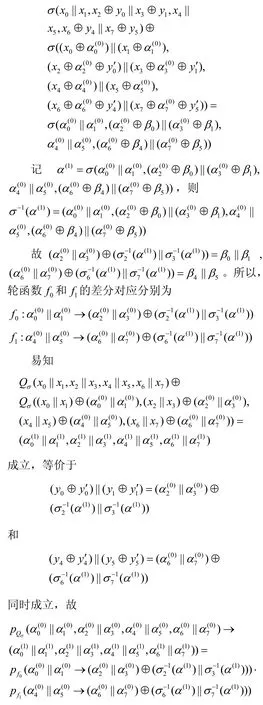
證畢。

由定理1，可得以下事實。

引理2對于任一σ-Piccolo 結構，以下3 個結論成立。

結論1一輪Piccolo 結構的活動指標大于或等于0。

結論22 輪Piccolo 結構的活動指標大于或等于1。

結論33 輪Piccolo 結構的活動指標大于或等于2。

證明1) 結論1 顯然成立，只證結論2 和結論3。

由備注2 知，活動指標與最后一輪輸出差分無關，從而為書寫方便，有時將差分特征的最后一輪輸出差分記為(* || *,* || *,* || *,* || *) 。

2) 由定理1，設σ-Piccolo 結構的2 輪差分特征為

3) 由定理1，設σ-Piccolo 結構的3 輪差分特征為

綜合情形1 和情形2，引理2 成立。證畢。

接下來，設(α0||α1,α2||α3,α4||α5,α6||α7)是σ-Piccolo 結構的輸入差分。若差分塊αi為非零差分塊，則用“1”表示；若差分塊αi為零差分塊，則用“0”表示，其中i=0,1,2,…,7。那么，σ-Piccolo結構的非零輸入差分恰好有28-1=255 種表示，即Δ1=(10000000),Δ2=(01000000),…,Δ255=(11111111)（這種表示方法不妨稱為“0”“1”表示）。易知，f0為活動輪函數當且僅當左起第1、2 位不全為零，f1為活動輪函數當且僅當左起第5、6 位不全為零。

首先，給出輸入輸出差分塊“0”“1”進行XOR運算需要滿足的運算規則：設a,b,c,d∈{0,1}分別是按照上述方法的“0”“1”表示，且設“∧”是按位與，“∨”是按位或。

性質2差分經過XOR 運算需要滿足以下條件：設α⊕β=γ，則

性質2 表示對于α⊕β=γ，當α,β至少有一個為零時，有c=a+b；當α,β都非零時，α⊕β=γ的值可能為零，也可能不為零，所以c=0或1。

性質3差分經過輪函數需要滿足以下條件：設f(α||β)=γ||δ，則

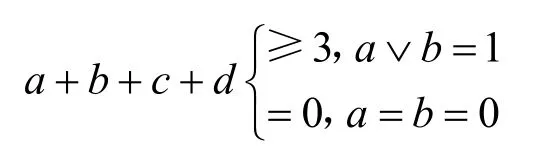
性質3 表示當輪函數的輸入差分非零時，有a+b+c+d≥ 3（因為輸入差分和輸出差分滿足性質1）；當輪函數的輸入差分為零時，輸出差分也為零。

根據性質2 和性質3，借助計算機，可以完成以下3 個實驗。

實驗1計算機搜索32 個σ-Piccolo 結構，給出所有第一輪的活動指標為0、第2 輪的活動指標為1、第3 輪的活動指標為1的3 輪差分特征的尾輪輸出差分（二進制）。

實驗1的具體結果如表2 所示。通過表2 發現，對于任一滿足條件的3 輪差分特征的尾輪輸出差分x0和x1至少有一個為“1”，和5x至少有一個為“1”，故可得以下結論。

表2 實驗1的具體結果

命題1對于任一σ-Piccolo 結構，設4 輪差分特征滿足第一輪的活動指標為0，第2 輪的活動指標為1，第3 輪的活動指標為1，則第4 輪的活動指標必為2。

引理3對于任一σ-Piccolo 結構，當輸入差分具有(0||0,α2||α3,0||0,α6||α7)形式時，以下3 個結論至少有一個成立。

結論1前2 輪Piccolo 結構的活動指標大于或等于2。

結論2前3 輪Piccolo 結構的活動指標大于或等于3。

結論34 輪Piccolo結構的活動指標恰為4。其中，α2||α3,α6||α7不全為零。

證明只需證明結論1 和結論2 都不成立時，必有結論3 成立即可。由引理2 知，2 輪Piccolo 結構的活動指標大于或等于1，3 輪Piccolo 結構的活動指標大于或等于2，從而只需證明前2 輪Piccolo結構的活動指標為1，且前3 輪Piccolo 結構的活動指標為2時，必有結論3成立即可。

定理2對于任一σ-Piccolo 結構，k(k≥ 1)輪Piccolo 結構的活動指標大于或等于k-1。

證明（數學歸納法）當k=1,2,3時，由引理2知，定理2 成立。

假設k＜l(l≥ 4)時定理2 成立，以下證明k=l時定理2 成立。

此時，由引理3，又可分為3 種情形。

綜合情形1 和情形2，定理2 成立。證畢。

實驗2計算機搜索32 個σ-Piccolo 結構，給出6 輪Piccolo 結構的活動指標的最小值。

因篇幅所限，這里只以塊移位變換σ=(72503614)為例給出實驗2的結果，具體如表3所示。其中第x（十六進制）行第y（十六進制）列交叉處的數值表示以(x y)為首輪輸入差分的6 輪Piccolo 結構的活動指標的最小值。例如，第3 行第e 列交叉處的數值為6，就表示以為首輪輸入差分的6 輪Piccolo 結構的活動指標的最小值為6。這里，行數和列數都從0 開始計算，另外，實驗結果表明，使活動指標的最小值為6的6 輪Piccolo 結構的非零輸入差分共有67個，使活動指標的最小值為7的6 輪Piccolo 結構的非零輸入差分共有164 個，使活動指標的最小值為8的6 輪Piccolo 結構的非零輸入差分共有24 個。

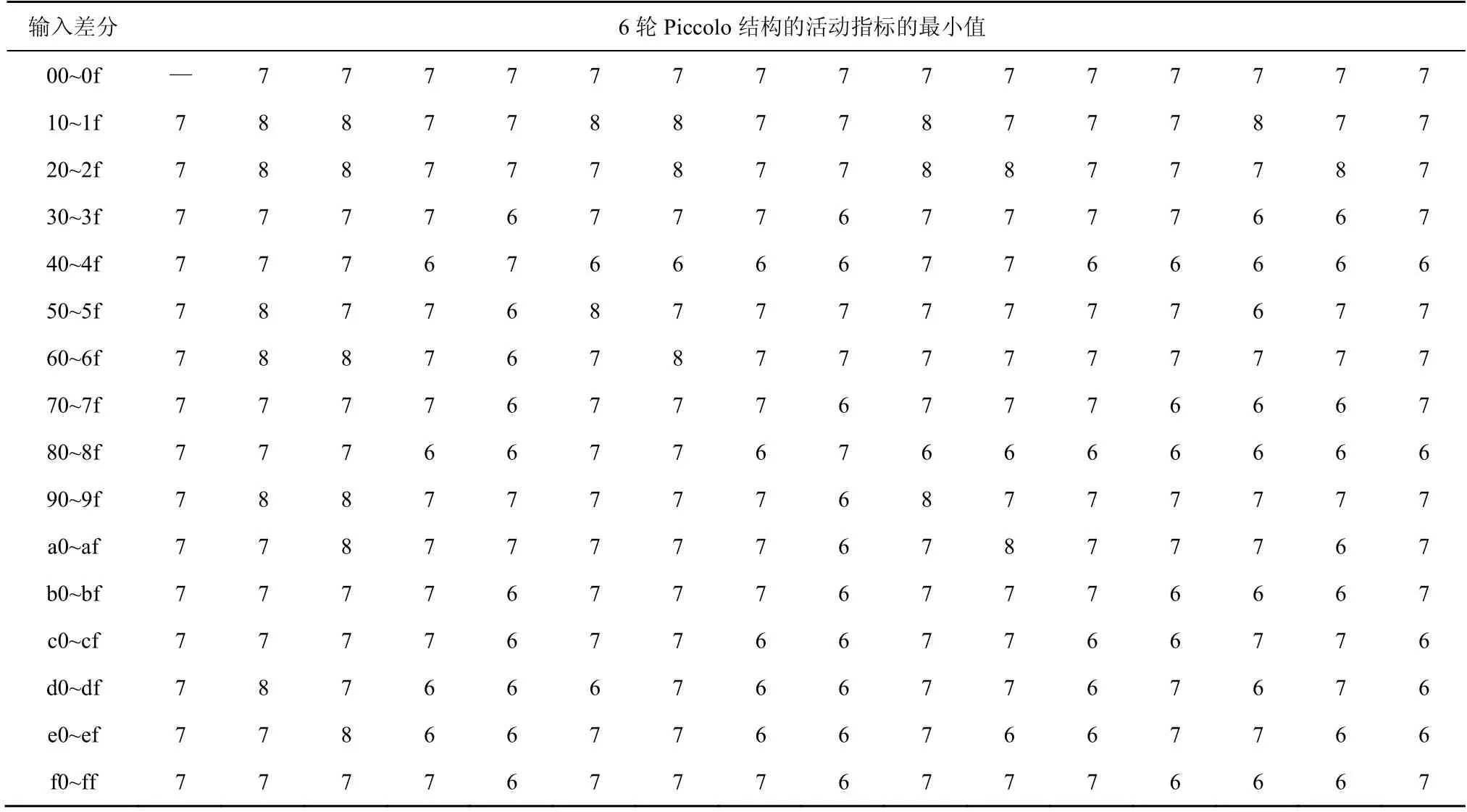
表3 實驗2的結果

實驗2 結果表明，有以下結論成立。

命題2 對于任一σ-Piccolo 結構，6 輪Piccolo結構的活動指標大于或等于6。

實驗3對于任一σ-Piccolo 結構，利用計算機篩選出活動指標為6的6 輪差分特征的尾輪輸出差分（十六進制），篩選出活動指標恰為k-1(k=1,2,3,4,5)的k輪差分特征的首輪輸入差分（十六進制）。

實驗3的具體結果如表4 所示。通過觀察表4發現，對于任一σ-Piccolo 結構，實驗3 中所求的尾輪輸出差分和首輪輸入差分沒有重合，故可得以下結論。

表4 實驗3的具體結果

命題3對于任一σ-Piccolo 結構，若6 輪Piccolo 結構的活動指標為6，則它的后面不可能“聯接”活動指標為k-1(k=1,2,3,4,5)的k輪差分特征。

引理4對于任一σ-Piccolo 結構，設為任一活動指標為6n的6n輪差分特征，則最后6 輪差分特征的活動指標必為6。

證明根據命題 2 可知，6 輪差分特征α(6n-6)→…→α(6n)的 活動指標≥ 6。若α(6n-6)→…→α(6n)的活動指標大于6，則6(n-1)輪差分特征α(0)→α(1)→ …→α(6)→ …→α(6n-6)的活動指標必小于6(n-1)，這與命題2 矛盾，故α(6n-6)→ …→α(6n)的活動指標必為6，引理4 成立。證畢。

定理3對于任一σ-Piccolo 結構，以下2 個結論成立。

結論1k(1≤k≤ 5)輪Piccolo 結構的活動指標大于或等于k-1。

結論2k(k≥ 6)輪Piccolo 結構的活動指標大于或等于k。

證明1) 結論1 由定理2 即可證明。

2) 當k=6n(n≥ 1)時，由命題2 可知，結論2成立。當k=6n+m(n≥ 1,1≤m≤ 5)時，分以下2 種情形進行討論。

情形1前6n輪Piccolo 結構的活動指標大于或等于6n+1。

此時，由定理 2 可知，后m輪差分特征α(6n)→…→α(6n+m)的活動指標大于或等于m-1，所以6n+m輪Piccolo 結構的活動指標大于或等于(6n+1)+(m-1)=6n+m。

情形2前6n輪Piccolo 結構的活動指標恰為6n時。

此時，設α(0)→ …→α(6n)→ …→α(6n+m)為任一6n+m輪差分特征，且6n輪差分特征α(0)→…→α(6n)的活動指標為6n。由引理4 知，α(6n-6)→ …→α(6n)的活動指標為6，再由命題3 和定理2可知，后m輪差分特征α(6n)→ …→α(6n+m)的活動指標大于或等于m，所以6n+m輪Piccolo結構的活動指標大于或等于6n+m。

綜合情形1 和情形2，定理3 成立。證畢。

由定理3 可得以下推論（注意：輪函數中的P變換的差分分支數為n+1 ）。

推論1對于任一σ-Piccolo 結構，以下2 個結論成立。

結論1k(1≤k≤ 5)輪差分特征中活動S盒的個數大于或等于(n+1)(k-1)。

結論2k(k≥ 6)輪差分特征中活動S 盒的個數大于或等于(n+1)k。

3 結束語

本文提出了類Piccolo 結構，并通過對差分傳遞規律的分析，得到了多輪類Piccolo 結構的活動輪函數和活動S 盒個數的一個下界。利用這些結果，結合輪函數或S 盒的最大差分概率，給出類Piccolo 結構的最大差分特征概率的上界。本文的研究結果對分組密碼的設計與分析具有較大的指導意義，但類Piccolo結構抵抗其他攻擊的能力如何值得進一步研究。