基于手性超結構設計的可變形機翼研究進展

劉凱 曹曉飛 李營 方岱寧

摘要：安全、穩定、高效是當前飛機機翼設計領域重點關注的問題。機翼是提供升力的主要部件之一，可變形機翼在改善飛機整體性能方面有巨大潛力。以智能材料為代表的新材料的發展對機翼柔性蒙皮、驅動裝置、控制技術以及輕量化結構產生了革命性的變革，拓展了手性拓撲結構的應用范圍。基于手性拓撲結構、飛機機翼的氣動性能分析、先進的制備工藝等技術而設計的變形機翼，可在不同飛行速度、飛行坡度以及周圍流場改變其機翼形狀，從而提高飛行效率，這是飛機機翼結構設計的前沿領域，也是未來重要的發展方向。本文介紹了手性超結構的設計方法及當前的研究現狀，總結闡述了當前國內外基于手性拓撲結構設計的可變形機翼的研究進展，為我國可變形飛機機翼的設計提供參考。

關鍵詞：變形機翼；柔性材料；手性拓撲結構；氣動性能；飛行效率

中圖分類號：224.3文獻標識碼：ADOI：10.19452/j.issn1007-5453.2022.01.003

基金項目：國家自然科學基金（11802030）

基于飛行工況進行機翼表面的主動形狀控制是飛機工程中最具挑戰性的問題之一。根據飛行高度、馬赫數以及飛機重量（質量）進行機翼外形設計，并對其外形參數進行優化是常用的機翼設計方法，這種設計方案形成的機翼具有固定的幾何形狀[1]。固定構型機翼可以保證飛行器在一種特定工況下性能達到最優。然而，隨著軍民領域復雜任務需求的增加，飛行器面臨空中偵察、搶險救災、遠程運輸、航空攝影等日益復雜多變的飛行環境，如在飛行時旋翼和機身會產生嚴重的氣動干擾現象，且該現象與飛行速度密切相關。因此，起降、巡航、高速飛行工況下對飛機機翼的外形參數均有不同的要求[2-3]。傳統固定構型的飛機機翼不能改變其機翼外形以適應不同的飛行工況，導致飛行器性能的損耗[4]。自飛機誕生以來，研究者們試圖利用仿生學的方法設計出能夠自主變化的機翼，以提高飛行效率。力學、材料、制造工藝以及控制技術等學科的快速發展為解決此類問題提供了技術基礎。

美國于1995年開展智能翼項目研究，截至今日，美國洛克希德-馬丁公司（Lockheed Martin Corporation）、新一代航空公司（NextGen Aeronautics）、波音公司（Boeing）、德國航空航天研究院（DLR）對陸續原有結構進行改進，分別提出折疊翼[5]、變后掠翼（MFX-1）[6]、展向自適應機翼[7]、MFC驅動機翼[8]等機翼形式，實現了飛行器性能和效率的大幅提升。基于新材料、新構型的智能變形機翼的研究已然邁入快速發展階段。

手性拓撲結構是由圓環節點和韌帶連接而組成的一種新型輕質多孔結構，通過圓環節點的旋轉和韌帶的彎曲變形可實現整體結構的變形，可滿足變形機翼輕量化、大變形、變形連續等需求。以北京理工大學、佐治亞理工學院等為代表的國內外高校對手性結構的動靜態力學性能表征、變形機理、結構創新及理論研究進行了大量研究。目前，基于手性結構設計的變形機翼的大多數研究還處在從概念設計到試驗表征的過渡階段，尚未投入大規模使用。

變形機翼涵蓋的范圍較廣，涉及的材料、構型種類眾多。本文著重研究了基于手性結構設計的變形機翼的研究現狀，綜合目前材料、力學、控制技術等領域的發展現狀，探究未來變形機翼的發展趨勢。

1發展現狀

1.1手性超結構

手性超結構由Kelvin于1894年提出。“手性”一詞最初用來描述物理幾何的關系，它的表述為：如果一個物體不可以由它的鏡像通過旋轉和平移得到，那么就稱其為手性[9]。

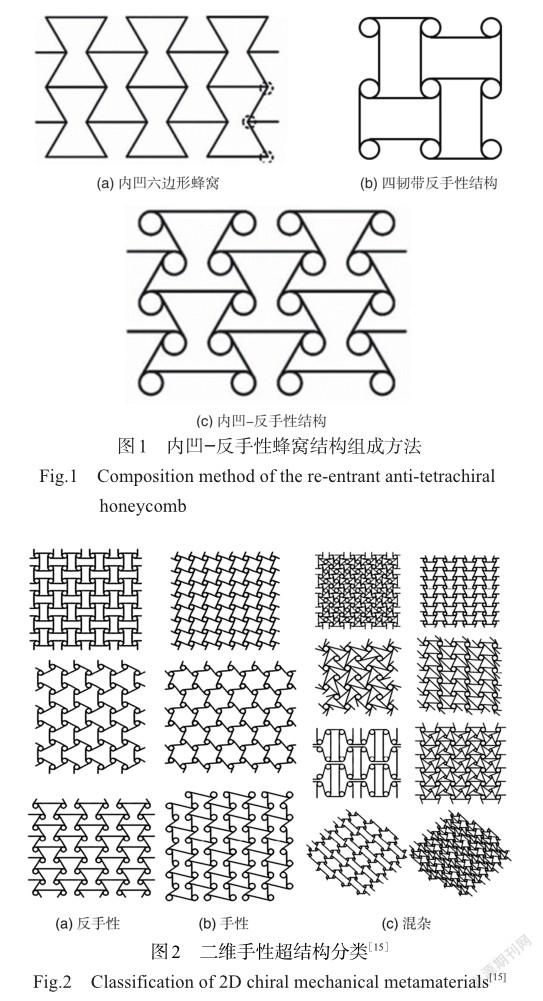
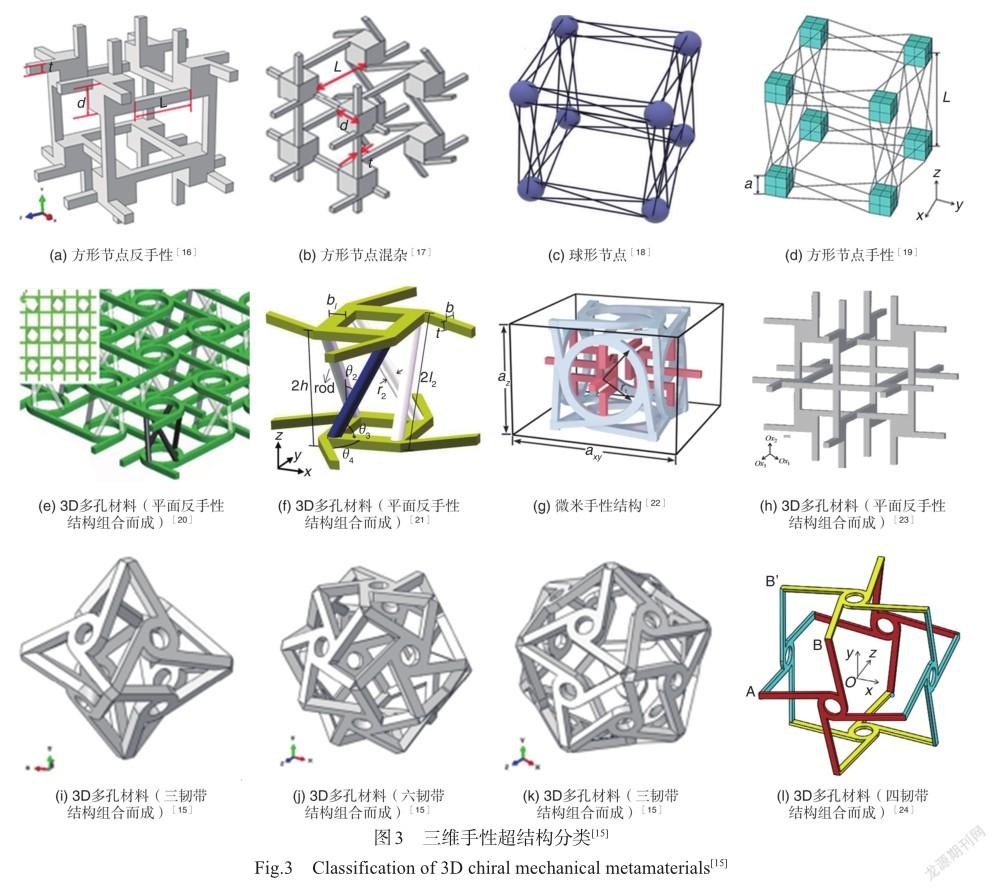
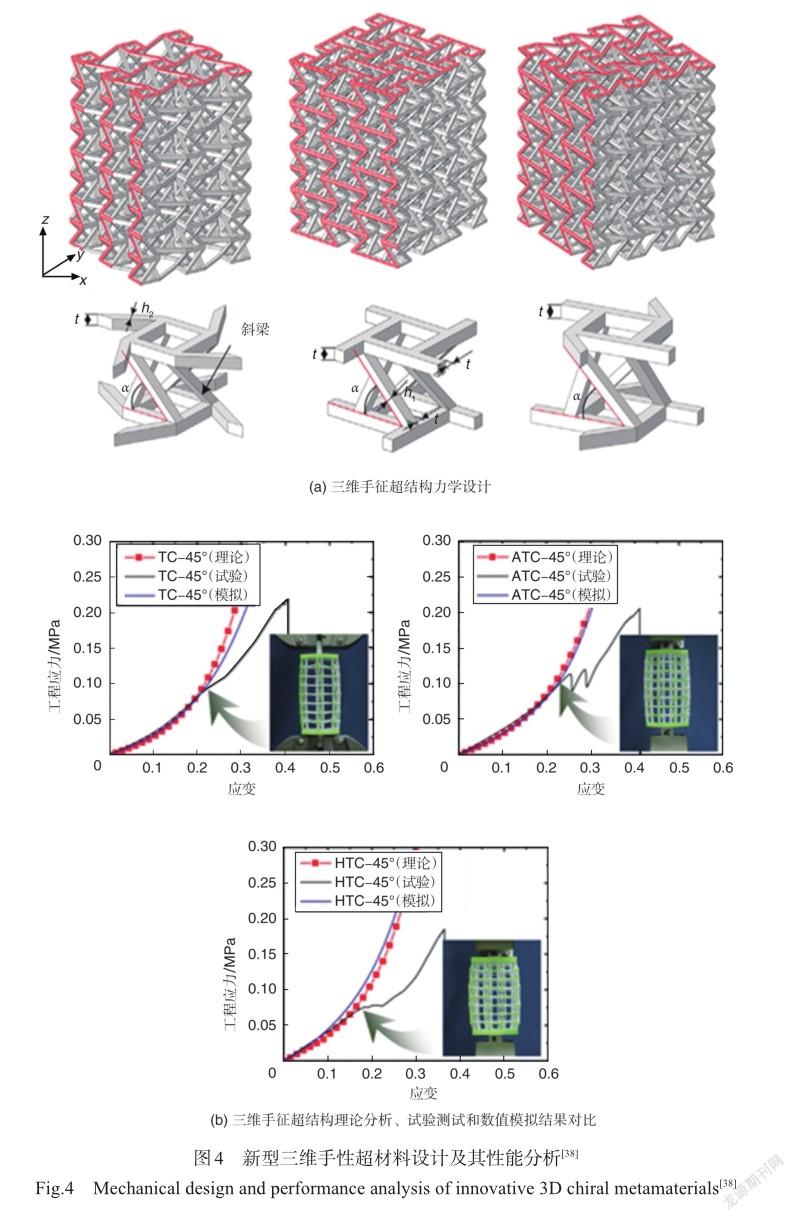
根據結構的特殊排列與空間維度，手性超結構可以分為二維手性結構和三維手性結構。二維手性結構是將節點和韌帶在二維平面上進行周期性排列形成的平面結構，在實際的模型制備時需要將平面結構沿著面外方向拉伸一定厚度。三維手性結構是由節點和韌帶在三維空間上按一定規則連接的三維結構。與二維平面結構相比，其構型更加復雜，種類更加豐富。根據圓環節點上連接的韌帶數目，可以分為三、四、六韌帶手性結構；根據韌帶和圓環節點的相對位置又可分為手性和反手性。前人的研究表明，反手性結構受到壓縮時韌帶兩端的圓環會朝不同方向旋轉，使得韌帶彎曲進而產生負泊松比效應。負泊松比結構不同于常規正六邊形蜂窩結構，它在軸向壓縮時，橫向會收縮，整體結構瞬時密度增加，瞬時彈性模量增加，引起結構剛度增加，可提高結構的承載能力，這一結論被郭亞鑫等[10]研究中的內凹蜂窩結構與傳統蜂窩結構的準靜態力學試驗證實。此外，負泊松比結構在承受面外載荷時胞壁易屈曲形成拱形，橫向曲率和彎曲的主曲率一樣，被稱為同向曲率或雙曲率現象，這種變形機制提高了面內切變模量和壓陷阻力[11]。而常規的正六邊形蜂窩在承受面外載荷時，會出現馬鞍形狀的反背曲率形變[12]，以該形狀作夾芯結構時會引起蒙皮的不連續變形[13]。魏路路等[14]將內凹六邊形蜂窩頂點替換為圓形節點，并將相鄰圓形節點采用反手性的連接方式得到內凹-反手性蜂窩，如圖1所示。與傳統蜂窩相比，內凹結構和圓環節點旋轉的協同作用使得該結構的能量吸收性能更強，負泊松比效應更加明顯[15-24]。因此，與傳統蜂窩結構相比，具有負泊松比效應的手性結構在飛行器變形結構等應用中稱為理想的結構材料。常見的二維、三維手性蜂窩結構分別如圖2和圖3所示。

1.1.1手性超結構理論研究

目前，關于手性超結構的理論研究多集中在探究手性蜂窩靜態力學性能與解釋負泊松比行為的機制上[25]。關于手性結構公式的推導多基于以下5個假設：（1）圓環節點是完全剛性的，即不考慮圓環節點的變形；（2）與施加載荷方向垂直的力忽略不計；（3）內力取決于觀察到的結構的變形；（4）韌帶的剪切變形與軸向變形忽略不計；（5）基于小變形假設，僅考慮韌帶的彈性彎曲變形而忽略塑性變形。

基于上述假設，國外學者Prall等[26]根據能量法，由傳統梁理論首次揭示了面內彈性模量、泊松比和結構參數的關系，并通過試驗證明了六韌帶手性蜂窩結構的泊松比為-1，該結果與理論模型吻合較好；Alderson等[27]認為上述方法沒有考慮到韌帶厚度與圓環重合的部分，提出了有效長度的概念，并推出了三、四韌帶手性/反手性和六韌帶手性蜂窩結構在小變形下的解析表達式。研究結果表明，在相同情況下，不同手性蜂窩結構在壓縮變形時的力學性能有很大差異，其中，三韌帶手性蜂窩結構的彈性模量最小；小變形情況下，四韌帶手性蜂窩結構的泊松比等于-1。Lorato等[28]進一步研究了三、四、六手性蜂窩結構的面外力學性能和結構幾何參數之間的關系，計算了不同手性蜂窩結構的切變模量以及橫向剪切剛度的Voigt以及Reuss邊界，研究結果對手性蜂窩結構的應用提供了理論指導。Bacigalupo等[29]基于微極彈性均質化和梯度均勻化方法探究了四、六韌帶手性蜂窩結構的均勻化問題，通過彈性模量解析表達式揭示了名義應變與非對稱應變在微極連續體的耦合關系。基于卡式定理，Mousanezhad等[30]系統推導了四、六韌帶手性/反手性結構的彈性模量和泊松比的解析表達式。

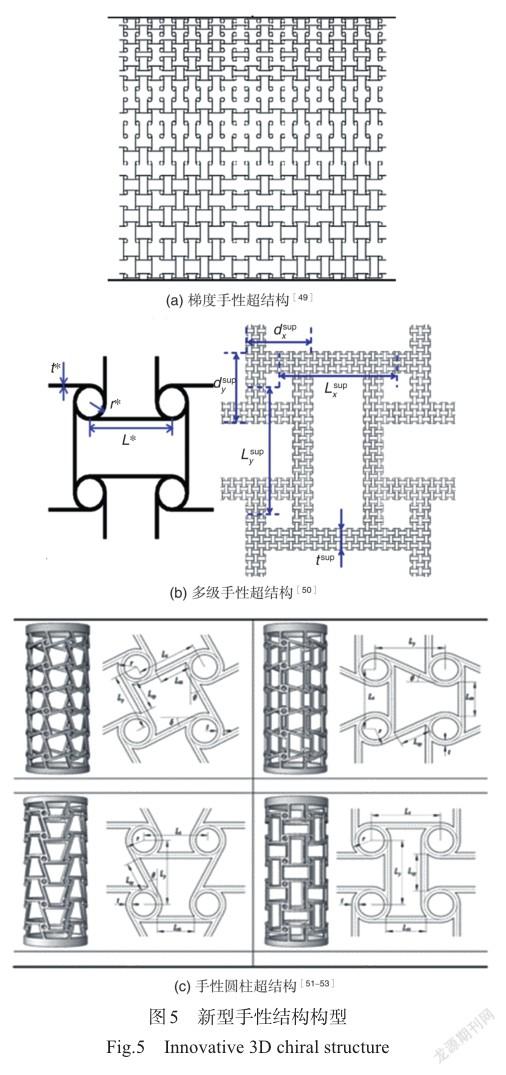
近年來，不僅僅國外學者展開了相關理論研究，國內學者在手性結構理論研究方面也取得了很大進展。針對現有的非中心對稱的微極理論無法表征二維手性結構的手性效應問題，Liu等[31]提出一種連續介質理論模擬二維各向同性手性結構的手性效應，并基于此方法確定了手性蜂窩材料的有效材料常數。該離散模型的精確解驗證了非手性模型無法預測的結果，很好地解釋了拉脹-旋轉以及剪切-旋轉等效應。Chen等[32]基于均勻化理論探究了韌帶長度不相等情況下的四邊反手性蜂窩結構的各向異性性能特征，通過研究其彈性力學性能常數與幾何參數之間的關系，得到了面內切變模量和泊松比封閉形式的表達式，該表達式對四邊反手性蜂窩結構的各向異性設計具有指導意義。基于手性蜂窩結構的旋轉機制，Fu等[21]將不同層的手性結構通過旋轉的韌帶連接設計出了三維手性結構，并基于梁理論和細觀力學推導了彈性模量和泊松比的解析表達式。Yuan等[33]構造了一種廣義的微極彈性均勻化方法來表征各向異性點陣中的方向模量、泊松比和耦合效應。研究結果表明，可以通過晶格結構的幾何重構來調整結構的各向異性。在手性結構大變形的理論研究方面，Zhong等[34]基于梁的大變形彎曲理論，利用橢圓積分方法推導了手性蜂窩結構的面內非線性力學本構關系，揭示了其非正交各向異性的性質。Hu等[35-37]基于試驗現象的觀測先后建立了三韌帶反手性蜂窩受不同方向壓縮的理論模型，該模型能夠很好地預測結構大變形時的泊松比變化和平臺應力。如圖4所示，Qi等[38]設計并通過理論、模擬和試驗研究了新型三維手性超材料的力學性能。上述研究為手性結構用于可變形機翼提供理論基礎。

1.1.2基于手性超結構的結構創新

隨著生物醫學、航空航天、智能制造等高端技術行業的不斷發展，傳統的蜂窩結構難以滿足高比吸能、大范圍泊松比可調可控以及輕量化等多種優良性能集于一體的多功能化需求，限制了行業和產業的發展。針對這一問題，一個較好的思路是通過創新結構設計來滿足多功能一體化需求。因此，國內外學者在結構創新方面做了大量工作。Alderson等[39]通過將傳統蜂窩結構中桿/板件角點替換為圓形節點設計了三韌帶手性/反手性以及內凹三韌帶手性/反手性結構。Lakes[40]基于將負熱膨脹材料與手性結構相結合的思想，設計并研究了具有負熱膨脹系數的手性超結構的力學性質。Ha等[19]將三維手性結構設計成具有拉扭耦合特性的立方體結構，并通過經典Cosserat彈性理論建立了該模型的本構關系。研究結果表明，該結構的泊松比具有明顯的尺寸效應。隨后，Ha等[41]還通過有限元分析進一步研究了三維各向同性手性結構的力學特性。除了周期性的規則設計之外，不規則和無序的手性超結構的力學性能也被學者們廣泛研究。Mizzi等[42-43]基于傳統六韌帶手性蜂窩結構提出了非周期性對稱的六韌帶手性蜂窩結構以及節點無序結構，實現了更大范圍的負泊松比調控，拓寬了手性蜂窩結構的應用場景。Pozniak等[44]探究了圓形節點大小隨機分布的反手性結構的負泊松比效應。

國內學者在結構創新方面也做了大量工作。Fu等[21]通過斜向扭轉韌帶將不同平面的二維手性結構連接，形成了平面內外均可扭轉的新型三維多孔材料。Chen等[32]設計了韌帶長度不等的四韌帶反手性蜂窩結構。Duan等[45]基于二維手性材料的拉扭耦合效應提出三維負泊松比材料設計方法，實現了泊松比和彈性模量在更大范圍的調控。Zhao等[46]設計并探究了四韌帶和六韌帶結構的形狀記憶效應，研究結果表明手性超結構在開發可編程超材料等方面具有很大的潛力。傳統的優化方法通常是改變圓環節點的形狀、韌帶和圓環節點的連接方式等，與基于優化算法的優化方法相比，存在用時時間長、魯棒性差、可解釋性不強、性能不能達到最優等缺點。近年來，拓撲優化、機器學習等優化算法為力學超材料在承受不同載荷下的優化設計提供了可行的技術支持。大連理工大學張會凱[47]基于獨立節點密度法、多材料模型和漸進均勻化理論設計的雙材料多孔負泊松比超材料比單一材料的承載能力、抗剪切能力更強。基于遺傳算法，Qiu等[48]對六韌帶手性蜂窩結構的形狀和尺寸進行優化，使得優化后的結構在大變形時彈性模量和泊松比保持在一定的范圍內，該結構的設計方法對飛機變形的設計具有重要意義。如圖5所示，北京理工大學的方岱寧課題組也開展了大量研究工作，并設計了梯度手性超結構[49]、多級手性超結構[50]和混合手性圓柱超結構[51-53]等創新構型，揭示了手性超結構用于可變形機翼的內在機制和變形機理。

1.2變形機翼

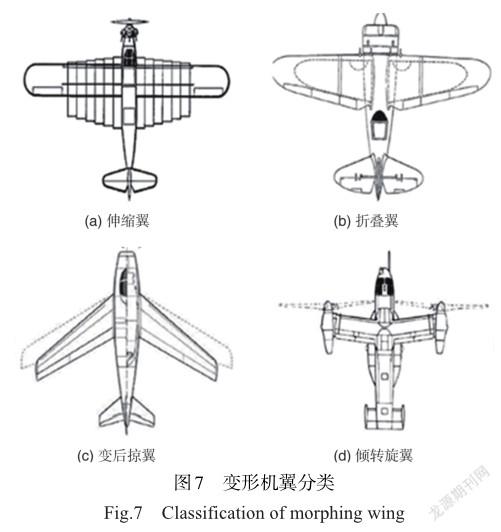
機翼是提供升力的主要部件，其面內設計參數主要包括展長、弦長、后掠角；面外設計參數主要包括扭轉剛度、翹曲度、彎度等[54]，這些結構參數與決定飛行器飛行狀態的升力系數、升阻比、外傾角等參數密切相關。變形機翼（morphing wings）也可稱為智能機翼（smart wings）、主動機翼（active wings）或自適應機翼（adaptive wings），能夠根據實際的飛行環境改變其外形參數，進而減少或消除顫振，減小氣動阻力，改善操縱特性，使得飛機在飛行任務中始終處于最優狀態[55-56]。此外，該機翼還可以擴展飛行器的飛行包線，減少襟翼式結構[57]。歐美等發達國家對變形機翼的研究起步較早，變形機翼的設計最早可追溯至1890年，Clement Ader基于蝙蝠外形而設計出具有可折疊翼的飛行器，并將其命名為“Eolo”，如圖6所示。但由于該設計只是簡單的模仿而缺乏一定的科學依據，最終以失敗告終。直至1903年，Wright兄弟設計出Wright Flyer I”并試飛成功，實現了人類的飛行夢想。此后30年間，歐美等國家先后開發出變后掠翼、伸縮翼、變展長、變弦長、變彎度等可變形機翼。自20世紀40年代開始，關于變形機翼的研究進入快速發展時期，如意大利、德國的Tornado、美國的X-5、F-111、XB-70，蘇聯的MAK-10、SU-17、MIG-23、TU-160等變體飛行器為該時期的典型代表[55]。由于早期的機械制造工藝、材料研究水平較低，飛行器結構設計往往比較復雜，機身只能采用剛度更大的材料，以滿足更高承載性和更快的飛行速度需求。機翼變形主要通過傳統機械式的剛性結構之間的滑動和轉動來實現。這種機翼結構需要多個鉸鏈和軸承的協同作用，雖然可以在一定程度上改善飛機性能，但驅動裝置、變體結構的使用，一方面對制造工藝、控制精度要求較高；另一方面增加了飛機結構的復雜程度，維護成本高，同時增加了飛機的重量（質量），限制了飛機的機動性、靈活性以及可操作性，無法滿足未來軍民領域對飛行器輕量化、智能化、信息化等多功能一體化的需求，因此無法廣泛適用飛行器結構。表1列舉了自1890年至20世紀80年代研發的部分變形機翼的型號與及其變形方式。經過近百年的發展，研究者基于變體結構設計了多種變體機翼。目前，關于變形機翼的分類有不同的標準，依據機翼的變形模式，本文將其主要類型大致分為伸縮翼、折疊翼、變后掠翼以及傾轉旋翼4種類型，結構示意圖如圖7所示。

在航空航天領域，變形機翼最重要的功能是為機翼提供連續變形的能力。新型變形機翼的研發已成為各國航空工業的重要任務之一。20世紀80年代以來，柔性材料的研究為解決飛行器高承載性和高機動性之間的矛盾提供了新的方案。同時，計算機仿真技術的發展極大地縮短了從設計到驗證所需的時間，力學體系的完善為機翼的可靠性驗證提供了理論指導。各國的研究者們從材料研究、制造工藝、結構創新、控制技術4個方面相繼提出不同構型、不同材料的變形機翼。

本文將變形機翼的發展歷程分為剛性變形階段和柔性變形階段。第一階段為1890年至20世紀80年代，這一階段機翼的材料主要為傳統的剛性材料，變形模式以剛性變形為主；第二階段為20世紀80年代后，這一階段的材料主要為柔性材料，變形模式以柔性變形為主。本文主要介紹柔性變形階段的機翼發展歷程。

1.2.1基于手性結構設計的變形機翼

近年來，在結構優化設計和材料選擇方面，多孔材料因其具有良好的比剛度、比強度以及吸能特性而得到廣泛關注。自然界中存在大量的多孔材料，如木材、蛋殼、蜂窩等，如圖8所示。根據構型排布特點，多孔材料可以分為兩大類：一類是泡沫材料/結構，其典型特征是構型無序，進一步地根據其內部結構的連通性可以分為開孔泡沫和閉孔泡沫；另一類是構型有序，排列呈周期性分布的多孔結構，其內部結構尺寸較為均勻，也稱為點陣結構。比較常見的點陣結構包括蜂窩結構、格柵結構、桿狀點陣結構等。手性蜂窩是一種有序的多孔結構/材料，與傳統的多孔材料相比，它具有豐富的變形模式、較高的可設計性以及多樣的設計參數。

由于傳統機翼結構的靈活性較差，基于仿生學思想，從結構設計的角度出發，1999年德國航空航天研究院（DLR）提出“手指概念”，其核心是一種由分離的板狀元件構成的柔性機翼，元件之間通過旋轉接頭連接而成。與傳統機翼結構相比，該機翼呈連續變化的弧度的外表面可為飛行器提供更好的升力和更小的阻力[58]。隨后，該研究機構針對機翼結構中梁、肋、桁條等零部件高度分化帶來的結構復雜、維修成本過高的問題，提出了皮帶-肋的自適應機翼的概念，這種設計方法是使用新的belt rib將原有零部件高度集中[59]。相比于傳統剛性變形翼形結構，這種設計方法的主要優勢在于：（1）零件大幅減少，維修成本低，質量輕；（2）承載能力強，強度大，可靠性高；（3）自主變形，無須借助主動驅動系統；（4）翼型產生連續變形，可控制機翼和葉片的氣動彈性和結構性能。

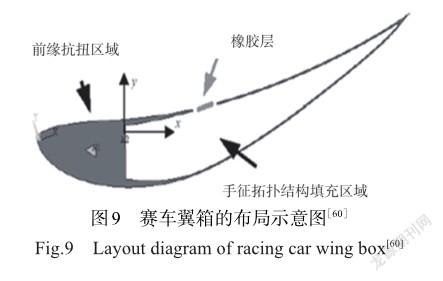
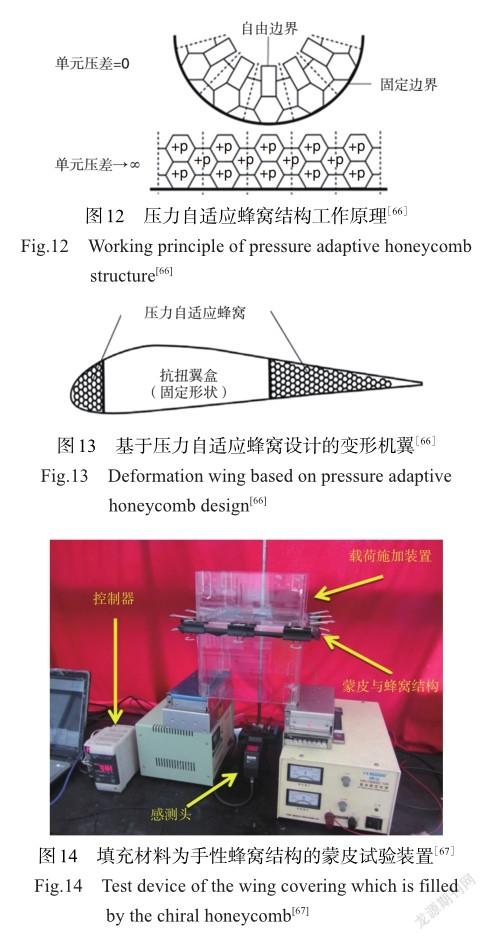
上述研究結果表明，連續變化弧度的外表面可提升飛行器性能。手性蜂窩的變形機制能夠很好地產生連續變形。手性蜂窩結構由圓環和韌帶組成，在變形過程中韌帶繞圓環節點旋轉，這種旋轉機制允許翼型截面在平面內產生連續的變形。受到上述研究的啟發，眾多學者開始思考將具有負泊松比特性的手性蜂窩結構用于變形機翼，以探究新結構對機翼性能的影響。然而，傳統制造工藝存在周期長、成本高、易產生缺陷等問題，難以發揮手性結構的優勢，極大地限制了手性蜂窩結構的工程應用。近年來，增材制造工藝以及計算機數值仿真技術的不斷發展解決了上述問題。2005年，謝菲爾德大學Bornengo等[60]以賽車車型Eppler 420為研究對象，首次將六邊形手性蜂窩結構作為賽車翼箱的芯層結構（見圖9）。2006年，佐治亞理工學院Spadoni等[61-62]研究了動態載荷下手性結構的頻響特性，采用動態形狀函數描述手性結構在寬頻率范圍內的變形行為。數值仿真結果與模態試驗表明，手性拓撲結構在固有頻率激勵時具有局部的形變特征，由此可利用共振效應來最小化局部變形出現所需的功率。基于前述研究，Spadoni等[63]隨后將手性結構應用于機翼結構，并通過計算力學和結構分析的物理耦合模型研究了手性拓撲結構對機翼氣動性能的影響，基于手性拓撲結構設計的機翼及試驗裝置如圖10所示。2008年，布里斯托大學Martin等[64]探討了基于手性蜂窩結構設計的被動變形機翼的弧度隨氣流的變化，試驗結果表明，機翼的變形與氣動載荷之間呈現非線性關系，通過調整手性蜂窩結構參數可改變機翼的外傾角，從而提供較高的變形能力，同時能保持機翼翼盒的結構完整性。2011年，韓國學者Heo等[65]以鋁合金為基體材料，基于手性蜂窩、六邊形蜂窩以及內凹六邊形蜂窩制備了三種不同類型的機翼結構（見圖11），采用流固耦合模型模擬機翼在流場作用下的變形能力。數值結果表明，以負泊松比蜂窩結構為芯層的機翼能夠兼顧剛度和柔性的需求，同時在相同的載荷時具有更低的局部應力。該研究表明，手性蜂窩結構具備用作被動翼型的潛力。2011年，代爾夫特理工大學Vos等[66]提出一種壓力自適應蜂窩結構（見圖12），該結構是利用蜂窩內的壓力來自發改變其結構的剛度和形狀，風洞試驗表明壓力自適應蜂窩可改變機翼部分的空氣動力學特性，基于壓力自適應蜂窩設計的變形機翼如圖13所示。趙顯偉[67]通過拉伸試驗和面外承載試驗證明手性蜂窩結構具有面內變形、面外承載的雙重作用，并將三、四、六韌帶手性/反手性蜂窩結構材料作為飛機機翼的填充材料，通過改變手性蜂窩結構參數可得到不同厚度的機翼蒙皮，氣動載荷試驗結果進一步表明手性蜂窩結構可滿足面內低模量和面外高承載需求，它是作為機翼蒙皮合適的填充材料。填充材料為手性蜂窩結構的蒙皮試驗裝置如圖14所示。

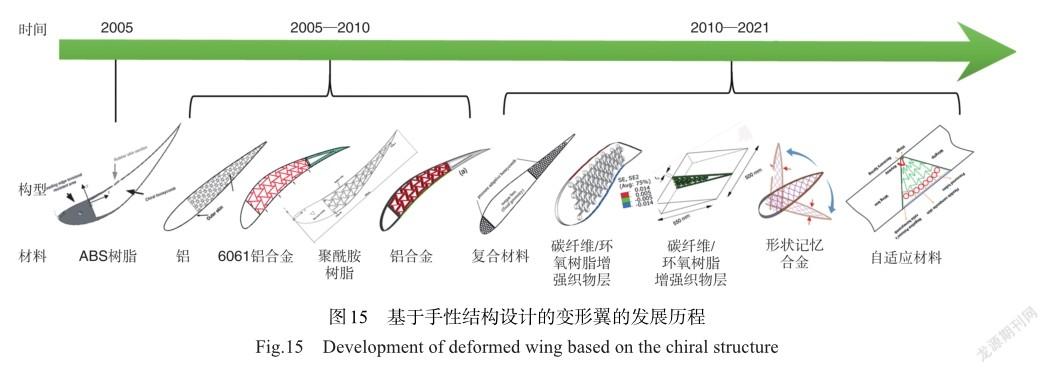
需要指出的是，由于需要同時滿足高承載和高機動性的需求，早期受限于材料科學的限制，機翼采用的材料多為金屬材料，這在一定程度上抵消了因結構設計帶來性能提升的優勢。因此，僅通過結構設計帶來性能的提升有限。隨著新材料的發展，研究者們開始將目標轉向新型材料的應用。圖15為近20年基于不同材料制備的手性結構機翼的發展歷程。從時間歷程可以看出，基體材料逐漸由樹脂、金屬鋁轉變為復合材料、智能材料和自適應材料。

1.2.2基于新材料設計的變形機翼

智能材料是20世紀90年代發展起來的一類新型功能材料。與傳統材料不同，智能材料通常以某一智能化體系方式存在，其定義為：由多種材料通過有機緊密復合或嚴格的科學組裝而成的材料系統[68]。智能材料種類眾多，其中，形狀記憶合金、壓電材料、形狀記憶聚合物、電流變材料、磁流變材料均可歸為智能材料[69]。在新材料中，復合材料常作為蜂窩結構的基體材料，形狀記憶合金、形狀記憶聚合物以及壓電材料等智能材料通常作為驅動器來驅動機翼的變形。

（1）復合材料

復合材料是將不同性質的材料通過先進的制備工藝組合而成的新型材料，相比于傳統的金屬材料，復合材料具有熱膨脹系數小、可設計性強、比剛度大、比強度大等特點，可滿足輕量化、高承載等需求，已逐漸成為交通運輸、航空航天領域關注的熱點[70-73]。

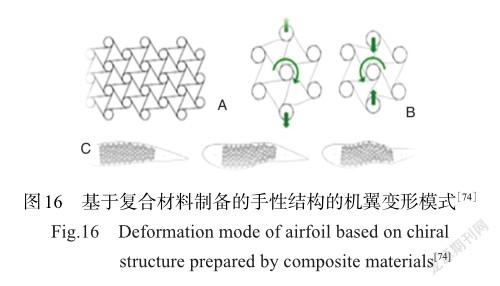
2010年，米蘭理工大學研究了基于長纖維增強聚合物制備的具有手性拓撲結構的復雜蜂窩結構在載荷作用下的變形模式和失效機理[57]；之后，他們又提出了復合材料手性蜂窩結構用作機翼內部柔性結構的解決方案。具體方法是在復合材料制備工藝中，將不同的單元黏合，在黏合過程中將彈性嵌件均勻壓在一起，由此產生的復合材料手性結構可以用非常薄的韌帶和不同類型的復合材料制成。同時，他們也提出了復合波紋層合板用作外部柔性蒙皮的設計方法：將蜂窩結構支撐的彈性層集成到波紋層合板中，以解決波紋板不規則的表面會增加氣動阻力并降低升力的問題[74]。基于復合材料制備的手性結構的機翼變形模式如圖16所示。2012年，西班牙航空公司研究了碳纖維/環氧樹脂增強復合材料的失效機理以及復合材料鋪層順序、手性結構幾何尺寸對機翼靜態和動態性能的影響[75]。結果表明，復合材料手性蜂窩芯用于氣動表面結構在有限的應變范圍內具有較大的弧度變化，并基于計算結果進行了數值優化。優化結果表明，在低速飛行模式下，升力曲線斜率增加一倍，在迎角范圍內增大了升力系數。以上研究均表明基于復合材料制備的手性結構用于變形機翼具有巨大潛力。

（2）形狀記憶合金

形狀記憶合金（SMA）材料因其具有獨特的形狀記憶效應、超彈性特性以及生物相容性等優勢，具有廣泛的應用空間和多元化的發展前景[76-77]。

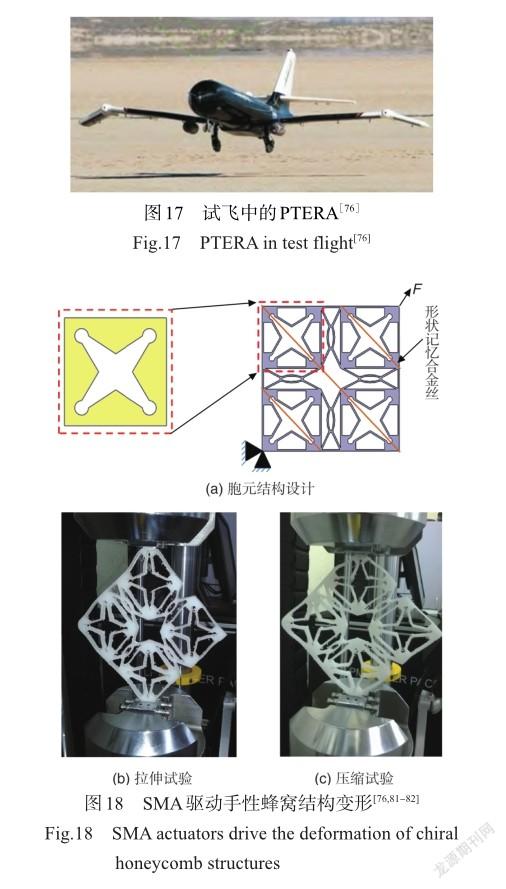
為探究形狀記憶合金材料對手性蜂窩結構力學性能的影響，2008年，謝菲爾德大學Hassan等[78]提出智能蜂窩結構的概念，該結構以形狀記憶合金為基體材料制備手性蜂窩結構，研究了該結構在準靜態壓縮下的泊松比變化歷程，并進一步探究智能蜂窩結構用作可展開桁架的變形行為。2012年，布里斯托大學設計了一種基于形狀記憶合金材料制備的天線，該天線由手性結構組成，具有可開展特性。模態分析表明該結構的模態響應的最小閾值滿足設計需求。目前，變形飛行器朝著小型化和輕量化的方向發展，這限制了電池的尺寸和容量。因此，飛行器的飛行時間和航程有限。機翼的變形需要驅動器的驅動，得益于材料的形狀記憶效應，基于形狀記憶合金制備的智能驅動器具有能量密度大、輸出位移/力高等優點。20世紀末至今，美國國防預先研究計劃局（DARPA）、美國空軍研究實驗室（AFRL）、美國國家航空航天局（NASA）等均展開SMA應用于機翼的研究[79]。如美國國家航空航天局（NASA）和波音公司合作研發的一種由SMA驅動的可變彎度后緣襟翼[80]，SMA驅動的可變翼梢小翼無人機PTERA[76]，如圖17所示。2014年，印度理工學院Prajapati等[81]將SMA驅動器嵌入手性蜂窩結構，為手性結構的變形提供能量。SMA驅動手性蜂窩結構變形如圖18所示。

（3）形狀記憶聚合物

形狀記憶聚合物（SMP）是一種可實現大應變的高分子聚合物，由于溫度變化會引起聚合物分子鏈的熔融結晶，因此會在聚合物中產生形狀記憶效應。相比其他形狀記憶材料，形狀記憶聚合物具有形變大、溫度轉換易控以及成本低等優勢[82-84]。

2014年，波士頓大學Rossiter等[85]利用熱響應形狀記憶聚合物（SMP）制備了六韌帶手性結構，通過熱循環試驗使其表現出自展開功能，并進一步研究了韌帶和圓環夾角對其變形性能和變剛度性能的影響。2017年，布里斯托大學Neville等[86]以剪紙技術Kirigami為設計靈感，使用SMP制備了具有可調變形和形狀變形性能的六邊形蜂窩結構。2018年，Huang等[87]將ABS塑料的內凹蜂窩結構用SMP的薄板相連接，由于SMP材料的形狀記憶效應，該結構表現出形狀記憶效應和變剛度特性，并通過試驗進一步研究了薄板厚度、溫度等對形狀記憶效應和變剛度性能的影響。基于形狀記憶聚合物制備的零泊松比蜂窩結構如圖19所示。SMP也可用作驅動器，2021年Tao等[88]基于蜂窩結構的接觸摩擦帶電波狀表面，設計了一種用于生物力學和無人機變形機翼能量收集的蜂窩式摩擦電納米發電機，能夠在飛行器飛行過程中收集機翼振動產生的動能并將其轉化為電能。變形機翼發電機裝置如圖20所示。

（4）壓電材料

壓電材料是一種具有壓電效應的多晶體，能夠將機械能和電能相互轉換，即材料尺寸的變化會產生電流，電流也會引起材料尺寸的變化。壓電效應的特殊性質決定了基于壓電材料的驅動器比傳統的機械式以及液壓式驅動器的響應速度更快、能量密度更大、結構更簡單且更易于控制，因此，被廣泛應用在結構振動、變形控制等方面[56-77]。因此，一般情況下，壓電材料較少地用于手性蜂窩的基體材料，而是為驅動裝置為結構的變形提供動力。

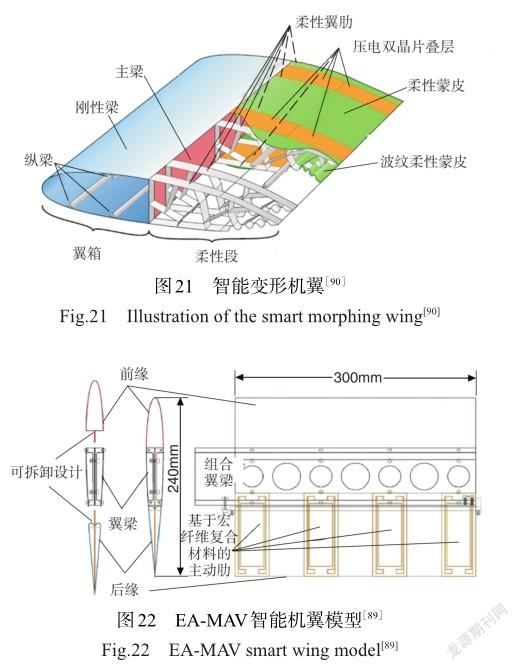
2011年，加拿大航空航天研究所Wickramasinghe等[89]提出以壓電陶瓷纖維作為主驅動機構，電活性聚合物作為輔助驅動機構的雙活性材料系統的智能變形機翼方案，如圖21所示。具體方法是在雙晶片驅動器外圍覆蓋一層預拉伸蒙皮，通過蒙皮的軸向壓縮載荷進而使驅動器產生壓電效應，最終發現這種設計方案可以提高機翼的變形能力。EA-MAV智能機翼模型如圖22所示。2019年，普渡大學Henry等[90]在NACA 0012翼型的基礎上進行改裝，內部結構使用桁架結構進而引導外層蒙皮的變形，采用壓電纖維復合材料（MFC）驅動器驅動整體結構的變形，并采用多學科優化技術對驅動方案以及蒙皮材料參數進行優化，最終使滾轉力矩增加27.67%，飛行速度提升83.4%。2020年，俄亥俄州立大學Chillara等[91]提出一種由壓電PVDF薄膜分層而成的雙穩態層合板，將壓電纖維復合材料、形狀記憶合金嵌入其中，利用壓電材料的壓電效應可有效捕捉由結構形變引起的電荷變化，進而將其轉化為電信號，可有效捕捉結構中的微小變形。

2當前研究面臨的難點

早期的變形機翼多采用傳統的機械或液壓驅動，機翼材料多為金屬材料，變形模式以剛性變形為主。近年來，隨著形狀記憶合金、壓電材料、復合材料、電感材料、可自愈材料等智能材料的興起，深度學習、強化學習、多傳感器融合等智能控制技術的發展，增材制造、復合材料成形工藝等先進制造方法的應用，非線性動力學、流固耦合等仿真技術的完善，推動變形機翼完成了由剛性變形階段到柔性變形階段的轉變。然而，基于手性結構設計的變形機翼的研究還存在以下幾方面問題。

（1）材料性能存在缺陷

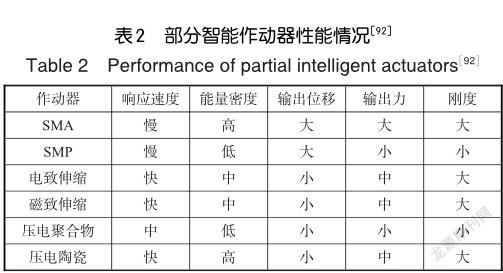
表2為幾種基于智能材料制備的智能作動器的性能對比，從表中可以看出沒有一種作動器能夠同時滿足響應速度快、能量密度高、輸出位移大、輸出力大、剛度大的需求。現代飛行器面臨更加復雜的飛行任務，需要進一步研發新材料以解決現有智能作動器的缺陷，同時更好地平衡飛行器面臨的高承載與高機動性之間的矛盾。

（2）結構設計較為單一

在手性超結構的胞元構型設計方面，主要研究對象仍以傳統節點-韌帶型手性結構為主，其韌帶多是實心的桿或板，不能滿足當前對結構設計輕量化、隔熱、抗爆、抗沖擊等多功能一體化的需求。目前，關于基于手性結構設計的變形機翼研究僅停留在二維層面，多數研究的結論僅是通過數值仿真得出的，缺乏試驗驗證。

（3）理論研究不夠完善

目前，關于手性結構的力學性能研究主要集中在準靜態面內力學和面外力學性能研究方面。在動態沖擊變形方面，還缺乏手性結構的沖擊吸能理論模型，有關實現結構的吸能效率和沖擊吸能能力方面的提升還需深入研究。另外，很多復合材料、形狀記憶合金以及形狀記憶聚合物等材料還缺乏準確描述其力學行為的本構模型。

（4）控制技術不夠全面

變形機翼的設計主要集中在結構設計以及材料選擇上，局限于驅動性能的研究以及一些靜態的分析，對于智能變形機翼的動態特性分析較少；非定常氣動力、柔性結構等因素使得飛行器的動力學模型往往涉及非線性、高維度、多參數等問題，增大了仿真求解時間，數值模擬難以做到與實際情況同步。強非線性對變形機翼的主動控制和精確驅動提出了更高的控制技術需求，而目前關于控制技術的研究仍不夠全面，僅僅處于起步階段。

3結束語

基于手性結構設計的變形機翼大多還處于試驗驗證階段，還未投入大規模量產。一方面，制造成形控制技術不夠成熟，在制造過程中會出現不可預測的缺陷，影響飛行器的安全；另一方面，實際飛行環境遠比試驗環境復雜，從概念設計到試驗驗證需要足夠的時間加以驗證。

智能材料、增材制造以及人工智能等技術的發展推動了變形機翼由剛性變形到柔性變形的轉變。近年來，變形機翼智能材料的本構理論及其可應用場景研究，增材制造成形缺陷理論及新成形工藝研究，機器學習、深度學習、強化學習等人工智能技術研究引起了廣泛關注。隨著增材制造工藝的發展與完善，變形機翼將很可能實現低成本、大尺寸、大規模和標準化生產。人工智能理論的發展將極大地推動多目標優化、拓撲優化等優化算法的求解效率。根據變形方式，本文將現有的變形機翼大致分為伸縮翼、折疊翼、變后掠翼和傾轉旋翼4類。在未來，隨著變形蒙皮、驅動裝置、變形機構、控制技術的發展，機翼的變形方式將會朝著多種變形組合的方向發展，輕量化多孔材料由傳統的設計到驗證的設計方法將難以滿足復雜動態多變的載荷需求。基于人工智能求解的優化方法將縮短結構優化時間，使得多孔材料能更好地滿足載荷需求，實現材料、結構和分布驅動參數的最佳匹配。

參考文獻

[1]Monner H，Sachau D，Breitbach E. Design aspects of the elastic trailing edge for an adaptive wing[R]. German Aerospace Center Braunschweig（Germany）Inst of Structural Mechanics，2000.

[2]靳鵬，樊楓.直升機機身干擾對旋翼氣動與噪聲特性影響研究[J].航空科學技術， 2021， 32（6）： 9-20. Jin Peng， Fan Feng. Study on the interaction influence of helicopter fuselage on the rotor aerodynamics and aeroacoustics[J]. Aeronautical Science & Technology， 2021， 32（6）： 9-20. （in Chinese）

[3]陳以金.變體飛行器柔性蒙皮及支撐結構性能研究[D].哈爾濱：哈爾濱工業大學， 2014. Chen Yijin. Study on flexible skin and supporting substructure ofmorphingaircraft[D].Harbin：HarbinInstituteof Technology， 2014. （in Chinese）

[4]孫楊，昌敏，白俊強.變形機翼飛行器發展綜述[J].無人系統技術， 2021， 4（3） ： 65-77. Sun Yang， Chang Min， Bai Junqiang. Review of morphing wing aircraft[J]. Unmanned Systems Technology， 2021， 4（3）： 65-77. （in Chinese）

[5]Bye D，Mcclure P. Design of a morphing vehicle[C]// Proceedingsofthe48thAIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，2007.

[6]Flanagan J，Strutzenberg R，Myers R，et al. Development and flight testing of a morphing aircraft，the NextGen MFX-1[C]// Proceedingsofthe48thAIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Conference，2007.

[7]Moholt M，Benafan O. Spanwise adaptive wing[C]//3rd Annual Convergent Aeronautics Solutions Showcase and Innovation Faire，2017.

[8]Monner H，Riemenschneider J，Opitz S，et al. Development of active twist rotors at the German Aerospace Center（DLR）[C]//Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference，2011.

[9]Thomson B K，Kelvin B，Thomson W. Baltimore lectures on molecular dynamics and the wave theory of light[D]. Cambridge：Cambridge University Press，2010.

[10]郭亞鑫，袁夢琦，錢新明，等.內凹型蜂窩結構在沖擊載荷作用下的力學行為及響應特性研究[J].中國安全生產科學技術， 2019， 15（12）： 5-10. Guo Yaxin， Yuan Mengqi， Qian Xinming， et al. Study on mechanical behavior and response characteristics of inner concave honeycomb structure under impact load[J]. Journal of Safety Science and Technology， 2019， 15（12）： 5-10. （in Chinese）

[11]Caddock B D，Evans K E，Masters I G. Honeycomb cores with a negative Poisson’s ratio for use in composite sandwich panels[C]//Proceeding of the Eighth International Conference on Composite Materials，1991.

[12]Evans K E. The design of doubly curved sandwich panels with honeycomb cores[J]. Composite Structures，1991，17（2）：95-111.

[13]邱克鵬，王智，王歡.手性性材料結構的等效力學性能分析計算[C]//第七屆中國航空學會青年科技論壇， 2016. Qiu Kepeng， Wang Zhi， Wang Huan. Calculation of equivalent elastic properities of chiral honeycombs [C]//The 7th Youth Science and Technology Forum of Chinese Aeronautical Society， 2016. （in Chinese）

[14]魏路路，余強，趙軒，等.內凹-反手性蜂窩結構的面內動態壓潰性能研究[J].振動與沖擊， 2021， 40（4）： 261-269. Wei Lulu， Yu Qiang， Zhao Xuan， et al. In-plane dynamic crushing characteristics of re-entrant anti-trichiral honeycomb[J]. Journal of Vibration and Shock， 2021， 40（4）： 261-269. （in Chinese）

[15]Wu W W，Hu W X，Qian G A，et al. Mechanical design and multifunctionalapplicationsofchiralmechanical metamaterials：A review[J]. Materials & Design，2019，180：107950.

[16]Xia R，Song X K，Sun L J，et al. Mechanical properties of 3D isotropic anti‐tetrachiral metastructure[J]. Physica Status Solidi（B），2018，255（4）：1700343.

[17]Wu W W，Qi D X，Liao H T，et al. Deformation mechanism of innovative 3D chiral metamaterials[J]. Scientific Reports，2018，8（1）：1-10.

[18]Duan S Y，Wen W W，Fang D N. A predictive micropolar continuum model for a novel three-dimensional chiral lattice with size effect and tension-twist coupling behavior[J]. Journal of the Mechanics and Physics of Solids，2018，121：23-46.

[19]Ha C S，Plesha M E，Lakes R S. Chiral three-dimensional lattices with tunable Poisson’s ratio[J]. Smart Materials and Structures，2016，25（5）：054005.

[20]Ebrahimi H，Mousanezhad D，Nayeb-Hashemi H，et al. 3D cellular metamaterials with planar anti-chiral topology[J]. Materials & Design，2018，145：226-231.

[21]Fu M H，Liu F M，Hu L L. A novel category of 3D chiral material with negative Poisson’s ratio[J]. Composites Science and Technology，2018，160：111-118.

[22]Frenzel T，Hahn V，Ziemke P，et al. Large characteristic lengths in 3D chiral elastic metamaterials[J]. Communications Materials，2021，2（1）：1-9.

[23]Farrugia P S，Gatt R，Grima J N.Anovel three‐dimensional anti‐tetrachiral honeycomb[J]. Physica Status Solidi（B），2019，256（1）：1800473.

[24]Fu M H，Zheng B B，Li W H. A novel chiral three-dimensional material with negative Poisson’s ratio and the equivalent elastic parameters[J]. Composite Structures，2017，176：442-448.

[25]盧子興，李康.手性和反手性蜂窩材料的面內沖擊性能研究[J].振動與沖擊， 2017， 36（21） ： 16-22. Lu Zixing， Li Kang. In-plane dynamic crushing of chiral and anti-chiral honeycombs[J]. Journal of Vibration and Shock，2017， 36（21）： 16-22. （in Chinese）

[26]Prall D，Lakes R S. Properties of a chiral honeycomb with a Poisson’s ratio of-1[J]. International Journal of Mechanical Sciences，1997，39（3）：305-314.

[27]Alderson A，Alderson K L，Attard D，et al. Elastic constants of 3-，4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J]. Composites Science & Technology，2010，70（7）：1042-1048.

[28]Lorato A，Innocenti P，Scarpa F，et al. The transverse elastic properties of chiral honeycombs[J]. Composites Science and Technology，2010，70（7）：1057-1063.

[29]Bacigalupo A，Gambarotta L. Homogenization of periodic hexa- and tetrachiral cellular solids[J]. Composite Structures，2014，116：461-476.

[30]Mousanezhad D，Haghpanah B，Ghosh R，et al. Elastic properties of chiral，anti-chiral，and hierarchical honeycombs：A simple energy-based approach[J]. Theoretical and Applied Mechanics Letters，2016，6（2）：81-96.

[31]Liu X N，Huang G L，Hu G K. Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices[J]. Journal of the Mechanics and Physics of Solids，2012，60（11）：1907-1921.

[32]Chen Y，Scarpa F，Liu Y，et al. Elasticity of anti-tetrachiral anisotropic lattices[J]. International Journal of Solids and Structures，2013，50（6）：996-1004.

[33]Yuan Z H，Cui Z M，Ju J. Micropolar homogenization of wavy tetra-chiral and tetra-achiral lattices to identify axialshear coupling and directional negative Poisson’s ratio[J]. Materials & Design，2021，201：109483.

[34]Zhong R C，Fu M H，Yin Q Y，et al. Special characteristics of tetrachiral honeycombs under large deformation[J]. International Journal of Solids and Structures，2019，169：166-176.

[35]Hu L L，Ye W K，Wu Z J. Mechanical property of antitrichiral honeycombs under large deformation along the xdirection[J]. Thin-Walled Structures，2019，145：106415.

[36]Hu L L，Wu Z J，Fu M H. Mechanical behavior of antitrichiral honeycombs under lateral crushing[J]. International Journal of Mechanical Sciences，2018，140：537-546.

[37]Hu L L，Luo Z R，Yin Q Y. Negative Poisson’s ratio effect of re-entrant anti-trichiral honeycombs under large deformation[J]. Thin-Walled Structures，2019，141：283-292.

[38]Qi D X，Zhang P，Wu W W，et al. Innovative 3D chiral metamaterials under large deformation：Theoretical and experimental analysis[J]. International Journal of Solids and Structures，2020，202：787-797.

[39]Alderson A，Alderson K L，Chirima G，et al. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs[J]. Composites Science and Technology，2010，70（7）：1034-1041.

[40]Lakes R. Cellular solid structures with unbounded thermal expansion[J].Journal of Materials Science Letters，1996，15（6）：1-10.

[41]Ha C S，Plesha M E，Lakes R S. Chiral three‐dimensional isotropic lattices with negative Poisson’s ratio[J]. Physica Status Solidi（B），2016，253（7）：1243-1251.

[42]Mizzi L，Attard D，Gatt R，et al. An analytical and finite element study on the mechanical properties of irregular hexachiral honeycombs[J]. Smart Materials and Structures，2018，27（10）：105016.

[43]Mizzi L，Attard D，Gatt R，et al. Influence of translational disorderonthemechanicalpropertiesofhexachiral honeycomb systems[J]. Composites Part B：Engineering，2015，80：84-91.

[44]Pozniak A A，Wojciechowski K W. Poisson’s ratio of rectangular anti-chiral structures with size dispersion of circular nodes[J]. Physica Status Solidi（B），2014，251（2）：367-374.

[45]Duan S Y，Xi L，Wen W W，et al. A novel design method for 3D positive and negative Poisson’s ratio material based on tension-twist coupling effects[J]. Composite Structures，2020，236：111899.

[46]Zhao W，Zhu J，Liu L W，et al. Analysis of small-scale topology and macroscale mechanical properties of shape memory chiral-lattice metamaterials[J]. Composite Structures，2021，8：113569.

[47]張會凱.拓撲優化方法的力學超材料設計[D].大連：大連理工大學， 2019. Zhang Huikai. Mechanical metamaterial design using topology optimizationmethod[D].Dalian：DalianUniversityof Technology， 2019. （in Chinese）

[48]Qiu K P，Wang R Y，Zhu J H，et al. Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation[J]. Chinese Journal of Aeronautics，2020，33（3）：902-909.

[49]Qi D X，Lu Q Y，He C W，et al. Impact energy absorption of functionally graded chiral honeycomb structures[J]. Extreme Mechanics Letters，2019，32：100568.

[50]Wu W W，Tao Y，Xia Y，et al. Mechanical properties of hierarchical anti-tetrachiral metastructures[J].Extreme Mechanics Letters，2017，16：18-32.

[51]Geng L C，Ruan X L，Wu W W，et al. Mechanical properties of selective laser sintering（SLS）additive manufactured chiral auxetic cylindrical stent[J]. Experimental Mechanics，2019，59（6）：913-925.

[52]Ma C，Lei H H，Liang J，et al. Macroscopic mechanical response of chiral-type cylindrical metastructures under axial compression loading[J]. Materials & Design，2018，158：198-212.

[53]Wu W W，Geng L C，Niu Y H，et al. Compression twist deformation of novel tetrachiral architected cylindrical tube inspired by towel gourd tendril[J]. Extreme Mechanics Letters，2018，20：104-111.

[54]段富海，初雨田，關文卿，等.變形機翼的發展現狀綜述[J].機電工程技術， 2021， 50（1）： 12-18. Duan Fuhai， Chu Yutian， Guan Wenqing. et al. A review of development status of morphing wing [J]. Mechanical & Electrical Engineering Technology， 2021， 50（1）： 12-18. （in Chinese）

[55]張堯，張婉，別大衛，等.智能變體飛行器研究綜述與發展趨勢分析[J].飛航導彈， 2021 （6） ： 14-23. Zhang Yao， Zhang Wan， Bie Dawei， et al. Review and development trend analysis of intelligent morphing aircraft [J]. Aerodynamic Missile Journal， 2021 （6） ： 14-23. （in Chinese）

[56]王曉明.壓電驅動柔性翼面的優化設計與變形控制方法[D].大連：大連理工大學， 2018. Wang Xiaoming. Optimal design and shape control method for piezo-actuatedflexiblewingsurface[D].Dalian：Dalian University of Technology， 2018. （in Chinese）

[57]Bettini P，Airoldi A，Sala G，et al. Composite chiral structures for morphing airfoils：Numerical analyses and development of a manufacturing process[J]. Composites Part B：Engineering，2010，41（2）：133-147.

[58]Vo？R，Strohmeyer D，Sachau D，et al. The Adaptive wing projekt（DLR）：Survey on targets and recent results from active/adaptive structures viewpoint[C]//Proceedings of the 10th International Conference on Adaptive Structures and Technologies（ICAST′99），1999.

[59]Campanile L F，Sachau D. The Belt-Rib concept：A structronic approach to variable camber[J]. Journal of Intelligent Material Systems & Structures，2000，11（3）：215-224.

[60]Bornengo D，Scarpa F，Remillat C. Evaluation of hexagonal chiral structure for morphing airfoil concept[J]. Proceedings of the Institution of Mechanical Engineers，Part G：Journal of Aerospace Engineering，2005，219（3）：185-192.

[61]Spadoni A，Ruzzene M. Numerical and experimental analysis of the static compliance of chiral truss-core airfoils[J]. Journal of Mechanics of Materials and Structures，2007，2（5）：965-981.

[62]Spadoni A，Ruzzene M. Static aeroelastic behavior of chiralcore airfoils[C]//Proceedings of ICAST-Sixteenth International Conference onAdaptive Structures and Technologies，2005.

[63]Spadoni A，Ruzzene M. Static aeroelastic response of chiralcore airfoils[J]. Journal of Intelligent Material Systems and Structures，2007，18（10）：1067-1075.

[64]Martin J，Heyder‐Bruckner J J，Remillat C，et al. The hexachiral prismatic wingbox concept[J]. Physica Status Solidi（B），2008，245（3）：570-577.

[65]Heo H， Ju J， Kim D M， et al. Passive morphing airfoil with honeycombs[C]//ProceedingsoftheASMEInternational Mechanical Engineering Congress and Exposition， 2011.

[66]Vos R，Barrett R. Mechanics of pressure-adaptive honeycomb and its application to wing morphing[J]. Smart Materials and Structures，2011，20（9）：094010.

[67]趙顯偉.可變形蜂窩結構的力學性能分析[D].哈爾濱：哈爾濱工業大學， 2013. Zhao Xianwei. The analysis of mechanical properties of morphing honeycomb structures[D]. Harbin： Harbin Institute of Technology， 2013. （in Chinese）

[68]白子龍.智能材料研究進展及應用綜述[J].軍民兩用技術與產品， 2020 （3） ： 15-20. Bai Zilong. Review on research progress and application of intelligent materials[J]. Dual Use Technologies & Products， 2020 （3） ： 15-20. （in Chinese）

[69]冷勁松，孫健，劉彥菊.智能材料和結構在變體飛行器上的應用現狀與前景展望[J].航空學報， 2014， 35（1） ： 29-45. Leng Jinsong， Sun Jian， Liu Yanju. Application status and future prospect of smart materials and structures in morphing aircraft[J]. Acta Aeronautica et Astronautica Sinica， 2014， 35（1）： 29-45. （in Chinese）

[70]王曦，付晨.復合材料轉向架構架及其疲勞損傷分析方法研究綜述[J].北京交通大學學報， 2019， 43（1）： 42-53. Wang Xi， Fu Chen. Review of composite bogie frame and its fatigue damage analysis methods[J]. Journal of Beijing Jiaotong University， 2019， 43（1） ： 42-53. （in Chinese）

[71]張恩奮.無人機結構用復合材料及其制造技術綜述[J].科技風， 2018 （11） ： 1. ZhangEnfen.Reviewofcompositematerialsand manufacturing technology for UAV[J]. Technology Wind， 2018（11） ： 1. （in Chinese）

[72]程健男，徐福泉，張體磊.樹脂基復合材料在直升機的應用及其制造技術[J].航空科學技術， 2021， 32（1） ： 109-114. Cheng Jiannan， Xu Fuquan， Zhang Tilei. Application and manufacturing technology of composites in helicopter[J]. Aeronautical Science & Technology， 2021， 32（1）： 109-114. （in Chinese）

[73]孫俠生，肖迎春，白生寶，等.民用飛機復合材料結構健康監測技術研究[J].航空科學技術， 2020， 31（7） ： 53-63. Sun Xiasheng， Xiao Yingchun， Bai Shengbao， et al. Research on structural health monitoring technology of civil aircraft composites[J]. Aeronautical Science & Technology， 2020， 31（7） ： 53-63. （in Chinese）

[74]Airoldi A，Bettini P，Boiocchi M，et al. Composite elements for biomimetic aerospace structures with progressive shape variation capabilities[J]. Advances in Technology Innovation，2016，1（1）：13.

[75]Airoldi A，Crespi M，Quaranti G，et al. Design of a morphing airfoil with composite chiral structure[J]. Journal of Aircraft，2012，49（4）：1008-1019.

[76]楊建楠，黃彬，谷小軍，等.形狀記憶合金力學行為與應用綜述[J].固體力學學報， 2021， 42（4）： 345-375. Yang Jiannan， Huang Bin， Gu Xiaojun， et al. A review of shape memory alloys： mechanical behavior and application[J]. Chinese Journal of Solid Mechanics， 2021， 42（4）： 345-375. （in Chinese）

[77]李繼威，張勇，陳繼春.壓電材料在飛行翼形控制方面的一些應用[J].電子元件與材料， 2009， 28（6）： 74-78. Li Jiwei， Zhang Yong， Chen Jichun. Application to control airfoil of aerocraft using piezoelectric materials[J]. Electronic Components & Materials， 2009， 28（6） ： 74-78. （in Chinese）

[78]Hassan M R，Scarpa F，Ruzzene M，et al. Smart shape memory alloy chiral honeycomb[J]. Materials Science and EngineeringA，2008，481（1）：654-657.

[79]顏碩.基于NiTi形狀記憶合金的柔性可變翼面設計[D].成都：電子科技大學， 2020. Yan Shuo. Research on morphing wing based on NiTi shape memory alloy[D]. Chengdu： University of Electronic Science and Technology of China， 2020. （in Chinese）

[80]Kamlet M，Gibbs Y. NASA tests new alloy to fold wings in flight[R]. NASA：Edwards，CA，USA，2018.

[81]Prajapati M，Mahapatra D R. Shape memory alloy-based active chiral composite cells[C]//Proceedings of the Active and Passive Smart Structures and Integrated Systems 2014，2014.

[82]Prajapati M，Mahapatra D R. Shape memory alloy-based active chiral composite cells[C]//Active and Passive Smart Structures and Integrated. International Society for Optics and Photonics，2014.

[83]劉京彪.形狀記憶聚合物及其復合材料性能與熱力學行為研究[D].哈爾濱：哈爾濱工程大學， 2020. Liu Jingbiao. Study on the performances and thermodynamic behavior of shape memory polymers and their composites[D]. Harbin： Harbin Engineering University， 2020. （in Chinese）

[84]杜海洋.形狀記憶聚合物的力學性能分析及其智能模具制備[D].哈爾濱：哈爾濱工業大學， 2018. Du Haiyang. Mechanical behavior analysis and smart mandrels fabrication based on shape memory polymers[D]. Harbin： Harbin Institute of Technology， 2018. （in Chinese）

[85]Rossiter J，Takashima K，Scarpa F，et al. Shape memory polymer hexachiral auxetic structures with tunable stiffness[J]. Smart Materials and Structures，2014，23（4）：045007.

[86]Neville R M，Chen J，Guo X，et al. A Kirigami shape memory polymer honeycomb concept for deployment[J]. Smart Materials and Structures，2017，26（5）：05LT03.

[87]Huang J，Zhang Q H，Scarpa F，et al. Shape memory polymer-basedhybridhoneycombstructureswithzero Poisson’s ratio and variable stiffness[J]. Composite Structures，2017，179：437-443.

[88]Tao K，Chen Z S，Yi H P，et al. Hierarchical honeycombstructured electret/triboelectric nanogenerator for biomechanical and morphing wing energy harvesting[J]. Nano-micro Letters，2021，13（1）：1-16.

[89]Wickramasinghe V，Chen Y，Martinez M，et al. Design and verification of a smart wing for an extreme-agility micro-airvehicle[J]. Smart Materials and Structures，2011，20（12）： 125007.

[90]Henry A C，Molinari G，Rivas-Padilla J R，et al. Smart morphing wing：optimization of distributed piezoelectric actuation[J].AIAAJournal，2019，57（6）：2384-2393.

[91]ChillaraV，RamanathanA，DapinoM.Self-sensing piezoelectric bistable laminates for morphing structures[J]. Smart Materials and Structures，2020，29（8）：085008.

[92]段富海，初雨田，關文卿，等.變形機翼的關鍵技術研究現狀及其展望[J].空軍預警學院學報， 2020， 34（3）： 203-209. Duan Fuhai， Chu Yutian， Guan Wenqing， et al. Research status and prospect of key technology of morphing wing[J]. Journal of Air Force Early Warning Academy， 2020， 34（3）： 203-209.（in Chinese）

Research Progress of Deformable Aircraft Wing Based on Chiral Superstructures Design

Liu Kai1，2，Cao Xiaofei1，2，Li Ying1，2，Fang Daining1，2

State Key Laboratory of Explosive Science and Technology，Beijing Institute of Technology，Beijing 100081，China

Abstract： Safety， stability and efficiency are the key issues in the field of aircraft wing structure design. Wing is one of the main components to provide lift， and deformable wing has great potential in improving the overall performance of aircraft. The development of new materials represented by smart materials has revolutionized the wing flexible skin， driving device， control technology and lightweight structure， and expanded the application range of chiral superstructures. The deformable wing designed based on chiral structure， aerodynamic performance analysis of aircraft wing and advanced preparation technology can change its wing shape at different flight speeds， flight slopes and surrounding flow fields， so as to improve flight efficiency， which is not only the frontier field of aircraft wing structure design， but also an important development direction in the future. This paper introduces the design method and theoretical method of chiral superstructures， and summarizes the research progress of deformable aircraft wing at home and abroad so as to provide

3336500338247