基于預訓練?微調策略的COVID?19 預測模型

楊 莉，萬旺根

（1.上海大學 通信與信息工程學院，上海 200444；2.上海大學 智慧城市研究院，上海 200444）

0 概述

2019 年末，新型冠狀病毒肺炎（COVID-19）由局部爆發逐漸演變為世界性大流行，截止到2020 年12 月23 日，COVID-19 已經造成全球超過7 800 萬人感染，累計超過170 萬人死亡。對確診病例數的準確預測能夠幫助決策者進行疫情預防控制措施和長/短期救治方案措施的制定［1-2］，這種措施的制定對于疫情的有效控制具有重要意義。

研究人員提出了大量數學模型對COVID-19 的擴散和傳播趨勢進行建模和預測。目前主流的傳染病模型主要可以分為3 類：第1 類是經典傳染病傳播模型，如SIR（易感者-患病者-康復者）［3-4］、SEIR（易感者-暴露者-患病者-康復者）［5-6］等；第2 類是基于深度學習的傳染病傳播模型；第3 類是其他模型，使用最廣泛的是復合群體模型［7-8］。經典傳染病模型在復雜多變的情況下（如政策和外部條件變化）需要手工分段設計以及參數估算，缺乏靈活性且效果不佳。復合群體模型對人群之間的遷移數據要求非常高，任何原始數據的缺陷都會導致模型預測誤差變大，難以在大樣本的場景下進行建模。因此，在復雜多變的環境下，基于深度學習的傳染病傳播模型逐漸成為研究熱點。然而，目前在COVID-19 研究方面存在數據量嚴重不足的問題，現有的監督學習方法不能很好地適應低數據量的場景，模型預測精度較低。

冠狀病毒在生物學特征上具有很大的相似性，有極為相似的病癥表現、傳染途徑以及發展趨勢，將這一特性作為建模因素，能夠使預測模型提前學習到病毒相關特征信息，有效輔助確診病例趨勢預測。本文構造基于預訓練-微調策略的COVID-19 預測模型P-GRU。在已有數據集上采用預訓練策略，使模型提前接觸到更多的疫情數據，從而獲得更充分的先驗知識。同時，將本地人為限制政策對疫情趨勢的影響考慮到模型中，在目標地區數據集中實現精準預測。

1 相關工作

1.1 COVID-19 傳播預測

在COVID-19 傳播預測方面，經典傳染病傳播模型通過數學建模來預測COVID-19 傳播的趨勢，如SIR 傳染病模型、改進的SEIR 模型等。雖然SIR模型及其變體可以略微捕捉到COVID-19 的傳播流行規律，但在實踐中仍然存在一定的問題。SIR 模型及其變體模型［9］在復雜多變的實際情況下缺乏靈活性，不能結合實際環境情況因素，如醫院的收治能力、不同患者的傳染率等，對于政策和外部情況的變化，模型需要手工分段設計和參數估算［10］，并沒有考慮很多外部因素對模型參數的影響，因此在預測結果上易出現較大偏差。復合群體模型考慮了人群的流動性對傳染病傳播的影響，適用于研究不同地區之間的病毒傳播情況，如傅家旗等提出的P-SI 模型［7］結合人口流動變化對COVID-19 傳播過程進行預測。雖然復合群體模型在一些場景下有著不錯的效果，但是一般而言，復合群體模型對不同群體的遷移數據要求非常高，原始數據的細微缺陷都會導致模型預測產生很大誤差。目前該研究更多局限在小樣本的情況下，且未考慮潛伏期的影響，對于大樣本等實際疫情復雜的情況，建模難度較大。

基于深度學習的預測模型通過多層非線性結構學習低維特征，形成更抽象的高維表示，具有強表達能力。CHIMMULA 等使用長短期記憶（Long and Short Term Memory，LSTM）網絡預測加拿大疫情的結束日期［11］，模型的短期精度為93.4%，長期精度為92.67%。ARORA 等使用LSTM 及其變體對印度的陽性病例數進行預測［12］，該方法的日預報誤差小于3%，周預報誤差小于8%。雖然采用LSTM 能夠較好地預測確診人數的整體趨勢，但LSTM 對某一參數的變化不敏感，如對于國家政策實施而導致某段時間內確診人數激增的情況難以進行有效預測。此外，HUANG 等提出用卷積神經網絡（Convolutional Neural Network，CNN）來分析和預測確診病例的數量［13］。然而，上述深度學習方法均沒有考慮到復雜多變的因素對疫情的影響。YANG 等考慮到部分外界因素對疫情的影響，結合社會經濟特征，基于門控循環單元（Gated Recurrent Unit，GRU）研究美國的流行病數據和疫情時間序列，進而對未來疫情傳播趨勢進行預測［14］。但監督學習對數據量的要求較高，數據量不足會導致模型預測效果不佳。

1.2 預訓練模型

預訓練模型是業內為解決目標問題而構建的已訓練好的模型。通過使用在其他問題上訓練過的模型參數作為當前任務模型參數的起點，能夠避免重新建立模型。在深度學習成為人工智能領域的主流方法后，預訓練模型被成功應用于各類計算機領域任務，如圖像分類、物體檢測等［15］。在自然語言處理領域，近幾年預訓練模型發展迅速，在大部分自然語言處理子任務中均取得了較高水準，包括序列標注、分類任務、句子關系判斷以及生成式任務［16］等。其中，預訓練-微調策略具有很強的可擴展性，在支持一個新任務時，只需要利用該任務的少量標注數據進行微調即可有效完成當前任務。

在COVID-19 數據集中，當前任務數據量不足會導致預測模型效果不佳，而不同地區的數據特征較為相似，因此，本文考慮采用預訓練-微調策略解決數據量不足這一問題。

2 P-GRU 預測模型

本文構建基于預訓練-微調策略的COVID-19 預測模型P-GRU。通過預訓練策略，在一定程度上解決數據量不足導致預測模型精度降低的問題，并為預測模型提供更豐富的初始化參數，從而使模型提前學習到COVID-19 的病毒本質規律，在新的數據集上進行微調后，針對確診病例發展趨勢具有較高的預測精度。

2.1 定義

2.2 預訓練-微調策略

預訓練-微調策略表示為：

其中：pretrain 作為一個函數，表示預訓練策略；fine_tuning 也是一個函數，表示微調過程。在源地區數據集A 上經過預訓練得到Modelpretrain，Modelpretrain在目標地區數據集B 上進行微調，得到最終模型Modelfinal，利用Modelfinal即可對目標地區的確診病例數進行預測。

在預訓練過程中，本文模型也考慮了本地人為限制政策對疫情趨勢的影響。經過預訓練后，保存訓練好的預訓練模型。利用在源地區中提前學習到的COVID-19 病毒本質規律，為后續的趨勢預測提供一個更好的初始化參數，將訓練好的模型和目標地區的疫情數據輸入到GRU 預測模型中，并在目標地區中經過微調后得到最終模型，利用此模型進行預測即得到在目標地區中的確診病例預測結果。預訓練策略示意圖如圖1 所示。

圖1 預訓練-微調策略示意圖Fig.1 Schematic diagram of pre-training and fine-tuning strategy

2.3 預測模型

通常利用回歸學習任務來解決預測問題，本文的預測模型包含一個用于趨勢預測的GRU 網絡。GRU 網絡通過適當地合并歷史信息來處理序列數據，并且能夠有效地簡化結構，相比于LSTM 網絡更加高效。本文預測模型架構如圖2所示，主要由嵌入模塊、遞歸模塊和輸出模塊實現。

圖2 P-GRU 預測模型架構Fig.2 Framework of prediction model P-GRU

預測模型有兩類輸入：一類是影響因素，另一類是流行病時間序列數據，如確診病例數。影響因素通過嵌入模塊作為GRU 的隱藏狀態的初始狀態，流行病時間序列數據通過GRU 的輸入端輸入模型，模型在時間序列上實現一個滑動窗口，使用帶有最近歷史信息的固定長度（L）序列來預測每個后續時間點。同時，為了使模型中的預測任務具備更好的合理性及可解釋性，滑動窗口固定長度的設定與COVID-19的潛伏期相關。輸出模塊則輸出預測值。另一個具有時變特征的輸入特征是本地限制政策［17］。由于本地限制政策的限制，在不同因素下，疫情的演變是不同的，因此本文在模型中加入本地限制政策的影響因素，如果在滑動窗口的長度L內有人為政策的限制，那么在隱式特征中加入本地限制政策的特征位，以一種隱式的方式考慮本地限制政策對疫情演變的影響。上述過程可由式（3）～式（6）表示：

在式（3）中，Embedding 表示嵌入模塊的實現，hid0表示遞歸模塊的初始狀態；在式（4）中，GRU 表示遞歸模塊GRU 神經網絡的實現；式（5）表示將靜態特征與本地限制政策的動態特征進行連接；在式（6）中，y't+1表示模型輸出的預測值，Wpredict表示最后一層輸出全連接層權重。

3 實驗與結果分析

3.1 實驗設置

3.1.1 數據集

本文實驗使用谷歌云平臺數據集，包含與COVID-19 相關的每日時間序列數據，遍布全球20 000 個不同位置。實驗采用的數據周期為2020 年1 月1 日—2020 年11 月26 日。實驗中選取了印度和美國兩個地區的數據，在印度地區數據集上進行預訓練，在美國地區數據集上進行微調。作為輸入的特征數據影響因素［18-20］包括靜態特征數據和動態特征數據影響因素。靜態特征數據影響因素包括當地人均GDP、人口統計數據、當地人的平均壽命等，動態特征數據影響因素包括COVID-19 病例數據（每日感染病例、累計感染病例、死亡數據）、政府干預政策數據等。同時，還有很多其他與疫情傳播有關的因素［21］。

3.1.2 評價指標

模型預測性能評價指標使用平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）和均方根誤差（Root Mean Square Error，RMSE）。MAPE 將精確度量化為一個比率，并可以確定為每個時間幀比率的絕對誤差百分比，即實際值減去預測值除以實際值；RMSE 則能夠衡量觀測值與真實值之間的偏差。MAPE 和RMSE 的計算公式分別如式（7）和式（8）所示：

3.1.3 對比模型

通過與當前主流模型進行比較，以客觀充分地驗證本文模型的有效性。實驗選擇CNN 模型、循環神經網絡（Recurrent Neural Network，RNN）模型、LSTM 網絡模型、GRU 模型和無預訓練策略的P-GRU 模型（No-pretrain-P-GRU）作為對比模型。

1）CNN 模型使用權重共享的概念，其訓練較為容易，且重要特征更能被有效提取［22］。1D CNN 可以用于時間序列分析，也可以用于分析具有固定長度周期的數據。當希望從整體數據集較短的片段中獲得重要特征，且該特征在數據片段中的位置不具有高度相關性時，1D CNN 是非常有效的。

2）RNN 模型包含跨時間分布的隱藏狀態，這使其能夠處理可變長度的連續數據［23］，因此在預測應用中最為常見，但RNN 的主要缺點是不能解決梯度消失或者梯度爆炸的問題，而且由于只涉及前一時間步［23］的隱藏激活功能，因此只能存儲短期記憶。

3）對于預測任務，LSTM 被認為是最可行的解決方法之一，其可根據數據集中存在的各種突出特征來預測未來趨勢變化。LSTM 是一種特殊的RNN，主要解決了長序列訓練過程中的梯度消失和梯度爆炸的問題［24］。LSTM 模型能夠將過去的隱藏狀態傳遞到后續階段中，相比于普通的RNN 模型，能夠在長序列中獲得更好的效果。

4）GRU 是循環神經網絡中的一種，和LSTM 一樣，也是為了解決長期記憶和反向傳播中的梯度問題而提出的，LSTM 和GRU 都是通過各種門函數來將重要特征保留下來，這樣就保證了信息在長期傳播時也不會丟失［25］。而且，GRU 相對于LSTM 少了一個門函數，GRU 只剩下兩個門，即更新門和重置門［26-27］，重置門決定了如何將新的輸入信息與前面的記憶相結合，更新門定義了前面記憶保存到當前時間步的量。因此，GRU 的參數量少于LSTM，整體上GRU 訓練速度快于LSTM。

3.1.4 參數設置

在印度數據集上預訓練時：嵌入模塊將4 維特定的靜態特征稀疏編碼為100 維度的向量；遞歸模塊是使用單層的具有100 維隱藏狀態的GRU 層，其采用嵌入層的嵌入結果作為第一個初始狀態，將長度為7 的滑動窗口狀態下的總確診病例數以及每天的本地限制政策作為輸入，若7 d 內有限制政策，則在隱式特征中加入標志位1，若在7 d 內沒有本地限制政策，則在隱式特征中加入標志位0；輸出層采用全連接層進行預測，通過最近7 d 攜帶的歷史信息來預測后續時間點的病例數。實驗使用Adam 優化器以1e-4 學習率訓練模型，損失函數采用RMSE。

在美國地區數據集［28］上進行微調時，與印度數據集上預訓練部分基本一致，但是遞歸模塊初始狀態的輸入除了嵌入層的嵌入結果，還將印度數據集上的預訓練模型結果也作為模型的一部分初始狀態。

3.2 結果對比

分別利用CNN、RNN、LSTM、GRU、No-pretrain-P-GRU 以及P-GRU 這6 個模型對美國數據集進行預測，并分別比較RMSE 以及MAPE。確診病例數歸一化后的模型RMSE 以及MAPE 結果如表1 所示。可以看出，在所有模型中，本文模型的RMSE 和MAPE 最小，由此表明其相比于其他模型更適合用于預測COVID-19 傳播趨勢。

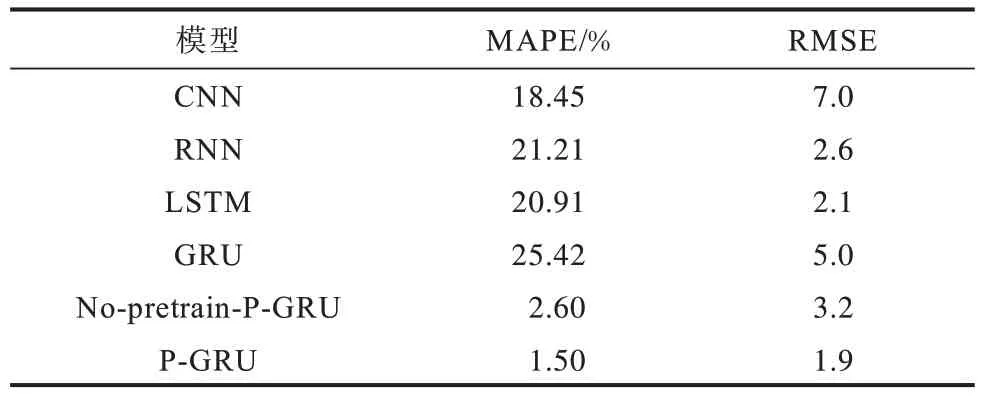
表1 不同模型的預測性能對比Table 1 Comparison of prediction performance between different models

4 結束語

本文提出一種結合預訓練-微調策略的COVID-19預測模型P-GRU，并在美國地區數據集上與CNN、RNN 等模型進行均方根誤差和平均絕對百分比的性能對比。實驗結果表明，本文模型基于監督學習，能在一定程度上解決數據量少而導致的模型精度不足問題，有助于提高確診病例趨勢預測性能。對于變異新冠病毒的傳播，也可采用本文提出的預訓練-微調策略對疫情傳播趨勢進行預測。下一步將深入分析外生因素對COVID-19 傳播的影響，并將其他與疫情傳播相關的因素作為特征加入模型，如口罩的流行率、人們的防護意識等，進一步提升模型對于新冠肺炎的預測精度。