基于改進邊界框回歸損失的YOLOv3 檢測算法

沈記全，陳相均，翟海霞

（河南理工大學計算機科學與技術學院，河南焦作 454000）

0 概述

目標檢測技術是很多計算機視覺任務的基礎，如實例分割［1-3］、圖像描述［4-5］、目標跟蹤［6］等，并且在工業(yè)、安防、視頻監(jiān)控、人臉識別［7］、機器人視覺［8］、自動駕駛［9］等諸多領域有極大的研究價值和應用前景，受到了學者們的廣泛關注。當前，目標檢測的研究已取得較大進展，檢測精度及速度在不斷提高。但是，由于尺度變化、旋轉、遮擋、光照以及物體的稠密度、角度等不同因素的影響，目標檢測的精度仍有較大的提升空間。近年來，基于深度學習的目標檢測成為研究熱點，卷積神經(jīng)網(wǎng)絡可以快速、準確地從大量樣本中學習更通用的特征，并且無需對樣品進行預處理，避免了復雜的手工制作和設計。

基于深度學習的目標檢測算法大致分為兩階段檢測算法和單階段檢測算法兩種：一種是包括R-CNN［10］、Fast R-CNN［11］、Faster R-CNN［12］和Pyramid Networks［13］的兩階段檢測算法，被稱為基于候選區(qū)域的目標檢測算法，其將目標檢測過程分解為候選區(qū)域提取、候選區(qū)域分類和候選區(qū)域坐標修正3 個步驟；另一種是包括SSD［14］、RetinaNet［15］和YOLO［16-18］系列的單階段檢測算法，被稱為基于回歸分析的目標檢測算法，其將目標檢測問題視為對目標位置和類別信息的回歸分析問題，通過一個神經(jīng)網(wǎng)絡模型直接輸出檢測結果。盡管存在這些不同的檢測框架，但無論對于單階段算法還是兩階段算法，邊界框回歸都是預測矩形框以對目標對象進行定位的關鍵步驟。

現(xiàn)有的目標檢測算法常用平均絕對誤差（Mean Absolute Error，MAE）損失（又稱L1 范數(shù)損失）、均方誤差（Mean Square Error，MSE）損失（又稱L2 范數(shù)損失）函數(shù)計算邊界框位置坐標的回歸損失，但是L1、L2 范數(shù)損失對邊界框的尺度具有敏感性，尺度越小的邊界框預測偏差對其影響越大，且卷積神經(jīng)網(wǎng)絡在評價邊界框的回歸效果時使用交并比（Intersection over Union，IoU）作為評價標準，而L1、L2 范數(shù)損失與IoU 之間的優(yōu)化并非等價。文獻［19］提出將IoU 作為邊界框回歸損失函數(shù)對檢測模型進行優(yōu)化，但是存在真值框與預測框無交集時優(yōu)化效果不佳的情況。文獻［20］提出一種通用的優(yōu)化邊界框的方式破折號GIoU，解決了在真值框和預測框無交集的情況下將IoU 作為邊界框損失函數(shù)不能反映邊界框之間的距離、以及函數(shù)梯度為零導致模型無法被優(yōu)化等問題。文獻［21］采用GIoU 損失對YOLOv2 模型損失函數(shù)進行改進，提高了模型對車身焊點的檢測精度。文獻［22］在YOLOv3 網(wǎng)絡中引入空間金字塔池化單元，并采用GIoU 損失計算坐標損失，在不降低速度的情況下，提高了無人機對罌粟的檢測效率。上述損失函數(shù)雖然總體上比傳統(tǒng)邊界框損失函數(shù)效果更好，但在某些情況下仍存在收斂效果不佳的問題。

本文提出邊界框回歸損失算法BR-IoU。將IoU作為邊界框回歸的損失項，加強損失函數(shù)的優(yōu)化與IoU 之間的聯(lián)系，并添加懲罰項加快真值框與預測框中心點之間的重疊速度，通過使預測框和真值框寬高比保持一致，提升邊界框的回歸收斂效果。

1 相關工作

1.1 IoU 與GIoU

交并比（IoU）也被稱為Jaccard 系數(shù)，用于衡量兩個邊界框重疊面積的相對大小，是2D 和3D 目標檢測中常用的評價標準。IoU 具有尺度不變性、非負性和對稱性，不僅可以用來確定正負樣本，而且還可以反映模型中預測框的檢測效果。如圖1 所示，A 和B 為2 個重疊的邊界框，其Jaccard 系數(shù)公式如下：

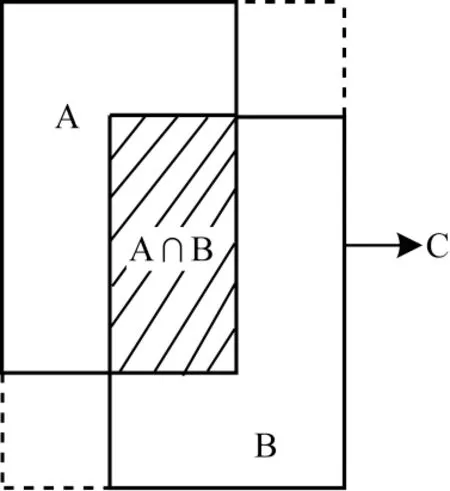
圖1 矩形A、B 與最小封閉框CFig.1 Rectangle A，B and the smallest enclosed frame C

將IoU 作為邊界框回歸損失，其損失函數(shù)如下：

雖然IoU 作為評價標準具有優(yōu)勢，但是當邊框無交集時將IoU 作為損失函數(shù)會導致無法反映兩個邊界框彼此之間的距離、損失函數(shù)梯度為零不能被優(yōu)化等問題。如圖2 所示，圖2（a）場景預測框的位置相較于圖2（b）場景離真實框更近，但是IoU 的值卻都為0。

圖2 邊界框無交集時IoU 的比較Fig.2 IoU comparison when bounding boxes have no intersection

基于此，2019 年REZATOFGHI 等［20］提出的GIoU繼承了IoU 具有的尺度不變性、非負性和對稱性，同時克服了IoU 在邊界框無交集情況下的不足。令圖1 中包含A 和B 的最小封閉框為C，則GIoU 公式如下：

當A、B 兩個邊界框完全重疊時，IIoU(A，B)=1；當A、B 兩個邊界框無交集時，IIoU(A，B)=0。因此，IoU的取值區(qū)間為［0，1］。而GIoU 的取值區(qū)間具有對稱性，即-1 ≤GGIoU(A，B)≤1，與IoU 相似：當兩個邊界框完全重疊，即|A ∪B|=|A ∩B|時，GGIoU(A，B)=1；當兩個邊界框無交集且距離無限大時，最小包圍框C的面積趨近于無窮大，此時GGIoU(A，B)=-1。

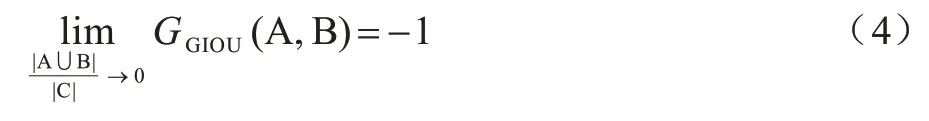
GIoU 取值區(qū)間的對稱性使其比IoU 更能反映邊界框的重疊和非重疊情況。本文將GIoU 作為邊界框回歸損失，其損失函數(shù)如下：

可以看出，邊界框之間的GIoU 值越大，GGIoU_loss值越小，邊界框的回歸收斂效果越好。

1.2 YOLOv3 模型

YOLOv3 模型是具有代表性的單階段目標檢測算法，其通過縮放、填充將不同尺寸輸入圖像的大小調整為32 的倍數(shù)，再分成S×S個非重疊的網(wǎng)格，如圖3 所示（S=7）。

圖3 輸入圖像網(wǎng)格示意圖Fig.3 Grid diagram of input image

每個網(wǎng)格負責檢測中心點位置坐標落入該格的物體，網(wǎng)格中預設有3 個邊界框和C個類別概率。在邊界框預測的5 個分量x、y、w、h和置信度中，（x，y）坐標表示邊界框的中心點相對于網(wǎng)格單元的位置，（w，h）坐標表示邊界框的尺寸，置信度用來判斷邊界框中存在物體的概率。YOLOv3 通過對置信度設定閾值過濾掉低分的邊界框，再對剩下的邊界框使用非極大值抑制（Non-Maximum Supression，NMS）算法去除冗余邊界框，得到預測結果，因此，YOLOv3每個網(wǎng)格有3×(5+C)個屬性值。為了加強對小物體的檢測性能，YOLOv3 借鑒了特征金字塔網(wǎng)絡（Feature Pyramid Network，F(xiàn)PN）的思想，采用多尺度特征融合的方式，在不同特征層對不同大小的物體進行預測。同時，YOLOv3 通過上采樣，自頂向下地融合底層的高分辨率信息和高層的高語義信息，提高了對不同尺度物體的檢測精度，尤其增強了對小物體的檢測精度。

YOLOv3 采用L2 范數(shù)計算邊界框坐標的回歸損失，L2 范數(shù)損失中不同尺寸邊界框對其預測框坐標產(chǎn)生偏差的敏感度也不同。相對于大尺寸邊界框，尺寸越小的邊界框預測偏差對其IoU 的影響越大，因此，YOLOv3 在邊界框位置損失部分乘以系數(shù)(2-tw×th)來緩解這一情況。為了實現(xiàn)多標簽分類，YOLOv3 采用二元交叉熵函數(shù)取代softmax 函數(shù)計算邊界框的類別損失。softmax 函數(shù)假設每個對象只屬于一個類別，但是在一些復雜場景下，一個對象可能屬于多個類別（例如女人和人），因此，在目標類別較復雜的數(shù)據(jù)集上，多標簽分類的二元交叉熵函數(shù)能取得更好的預測結果。YOLOv3 網(wǎng)絡模型的損失函數(shù)分為邊界框坐標損失、置信度損失和分類損失。損失函數(shù)如式（6）所示：

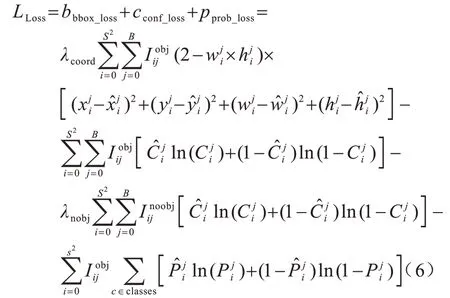
圖4 YOLOv3 算法檢測過程Fig.4 Detection process of YOLOv3 algorithm

2 BR-IoU 邊界框回歸損失算法

采用L2 范數(shù)邊界框回歸損失函數(shù)的YOLOv3檢測算法通常會出現(xiàn)以下2 個問題：

1）如圖5 所示，4 組邊界框角點坐標距離的L2 范數(shù)損失值相等，但IoU 值卻不同，這表明L2 范數(shù)損失不能準確地反映IoU 值的變化，與IoU 之間不具有強相關性。

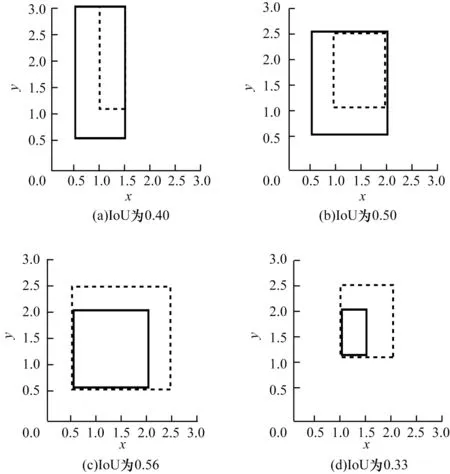
圖5 L2 范數(shù)損失值相等時IoU 的變化Fig.5 Change of IoU when L2 norm loss values are equal

2）L2 范數(shù)損失具有尺度敏感性，在算法訓練過程中，當兩個邊界框的IoU 值相同時，大尺寸邊界框會產(chǎn)生更多的損失值使小尺寸邊界框難以被優(yōu)化，導致算法對小尺寸目標的檢測效果不佳。

針對上述問題，本文提出BR-IoU 算法，為方便不同邊界框損失算法的性能對比，將BR-IoU 算法分為BR-IoU-A 算法和BR-IoU-B 算法。

BR-IoU-A 算法將IoU 作為邊界框回歸的損失項，強化與IoU 之間的聯(lián)系，并繼承了IoU 的尺度不變性，使得不同尺度的邊界框在回歸過程中獲得更均衡的損失優(yōu)化權重。然后算法在IoU 損失項的基礎上添加一個懲罰項，通過最小化預測框與真值框中心點圍成矩形的面積，加快預測框中心點與真值框中心點的重疊速度。算法的懲罰項使邊界框在任何情況下都存在梯度，在邊界框無交集的情況下仍然能夠反映邊界框間的相對距離，為邊界框的優(yōu)化提供移動方向，如圖6 所示，D 是真值框Bg的中心點bg和預測框B 的中心點b 圍成的矩形框，Bc是真值框Bg與預測框B 的最小封閉框，w和h為D 的寬和高，wc和hc為Bc的寬和高，則BR-IoU-A 計算公式如下：

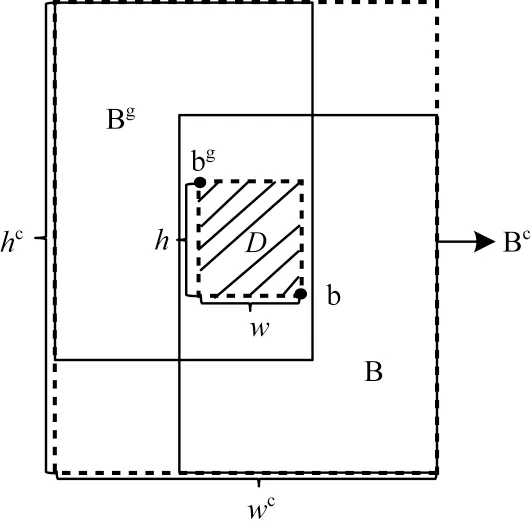
圖6 BR-IoU-A 算法示意圖Fig.6 Schematic diagram of BR-IoU-A algorithm

利用BR-IoU-A 算法計算邊界框回歸損失，損失函數(shù)如下：

BR-IoU-A 損失繼承了IoU 和GIoU 損失的優(yōu)良屬性：1）BR-IoU-A 損失對邊界框的尺度不敏感，具有尺度不變性；2）BR-IoU-A 損失在邊界框無交集情況下仍然存在損失梯度，可以為邊界框的優(yōu)化提供移動方向；3）當兩個邊框完全重疊時，GGIoU=BBR-IoU-A=1，GGIoU_loss=BBR-IoU-A_loss=0；當兩個邊框距離無限遠時，GGIoU=BBR-IoU-A=-1，GGIoU_loss=BBR-IoU-A_loss=2。但在某些情景下，如圖7 所示（其中，實線框為真值框，虛線框為平面測框），真值框寬和高的值都為1，預測框寬和高的值為0.5。此時無論預測框與真值框的中心點間的距離如何變化，GIoU 與IoU 損失值都不變，由此可見，BR-IoUA 損失算法能很好地區(qū)分邊界框之間的重疊情況。

圖7 中心點間相對位置比較Fig.7 Comparison of relative positions between center points

圖7（a）圖像的檢測效果優(yōu)于圖7（b）圖像，BR-IoU-A 損失算法通過值的變化來反映這種情況。

算法BR-IoU-A 邊界框回歸損失算法

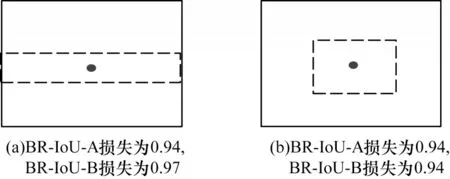
圖8 預測框不同寬高比下的檢測效果對比Fig.8 Comparison of detection effects under different aspect ratios of predicted bounding boxes

圖8（a）預測框的寬高比值相較于圖8（b）預測框更接近真實框，預測效果更好，但BR-IoU-A 值卻相同。因此，本文在BR-IoU-A 的基礎上，結合預測框與真值框之間寬高比的一致性提出BR-IoU-B 損失算法，計算公式如下：

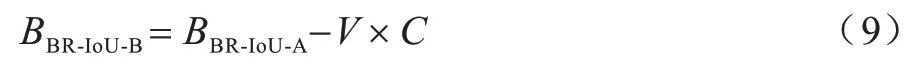
其中，參數(shù)V使預測框寬高比與真值框的保持一致，C是V的平衡參數(shù)，當兩個邊界框無交集或IoU 值較低時，使邊界框之間的重疊因子在回歸過程中獲得較高優(yōu)先級，從而加快邊界框回歸的收斂速度。

其中：wg、hg分別為真值框的寬和高；wp、hp分別為預測框的寬和高。綜上，BR-IoU-B 損失函數(shù)如下：

使用BR-IoU 邊界框回歸損失算法對YOLOv3模型進行改進，改進后的損失函數(shù)如下：

3 實驗結果與分析

本文實驗模型基于Tensorflow1.13.1 框架，編程語言為python3.7，實驗操作系統(tǒng)為Ubuntu16.04，GPU型號為NVIDIA Tesla P40，CUDA版本為10.0。為了驗證BR-IoU算法的實際性能，將原始YOLOv3的邊界框回歸損失部分分別替換成GIoU 損失算法（簡稱G-YOLO）、BR-IoU-A 損失算法（簡稱BR-YOLO-A）、BR-IoU-B損失算法（簡稱BR-YOLO-B）。在PASCAL VOC 2007+2012 數(shù)據(jù)集和COCO 2014 數(shù)據(jù)集上進行模型評測和對比實驗。

在算法訓練過程中，為了增強模型性能，對數(shù)據(jù)集中的原始圖像進行數(shù)據(jù)增強操作，通過圖像隨機裁剪、旋轉、平移、顏色變化等方法，增加圖像的多樣性，使神經(jīng)網(wǎng)絡具有更強的泛化效果，提高模型魯棒性。此外，為檢測不同尺度圖像中包含的不同尺度和形狀的目標，在每個檢測層中設定不同尺度的先驗框與真實標簽進行匹配。網(wǎng)絡輸入大小為416×416，模型參數(shù)更新方式為Adam，初始學習率為0.000 1，權重衰減設置為0.000 5。對于VOC 和COCO 數(shù)據(jù)集，模型加載預訓練權重來完成初始化，令其他沒有預訓練權重的部分在訓練過程中自適應微調參數(shù)，然后訓練整個模型。為了在訓練過程中使模型穩(wěn)定，算法為模型訓練設置兩個輪次迭代的熱身階段。實驗采用平均精度（Average Precision，AP）反映每一類目標的檢測效果，平均精度是從準確率和召回率兩個方面來衡量檢測算法的準確性，可以直觀地表現(xiàn)模型對單個類別的檢測效果；采用平均精度均值（mean Average Precision，mAP）來衡量多類目標的平均檢測精度，mAP 值越高，模型在全部類別中綜合性能越高。

3.1 在PASCAL VOC 數(shù)據(jù)集上的對比實驗

PASCAL VOC 2007+2012訓練集共包含16 551張圖像、40 058 個樣本框，分為4 個大類和20 個小類。VOC 2007 測試集包含4 952 張圖像、12 032 個樣本框。PASCAL VOC 通過計算數(shù)據(jù)集IoU=0.5 時的mAP 對模型進行評價。該組實驗在PASCAL VOC數(shù)據(jù)集上的訓練迭代次數(shù)為100 輪，測試集上的mAP 及各類別目標的AP 檢測結果如圖9 和表1所示。

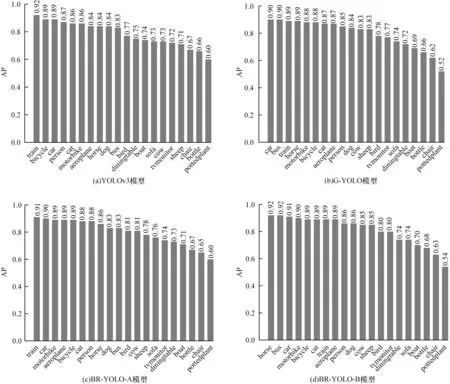
圖9 PASCAL VOC 數(shù)據(jù)集上不同算法的AP 對比Fig.9 AP comparison of different algorithms on PASCAL VOC data set

表1 PASCAL VOC 數(shù)據(jù)集上不同算法的性能對比Table 1 Performance comparison of different algorithms on PASCAL VOC data set

實驗結果表明，在不影響模型檢測速度的情況下，BR-YOLO-B 算法的mAP 高出原YOLOv3 算 法2.54 個百分點，高出G-YOLO 算法1.51 個百分點。

3.2 在COCO 數(shù)據(jù)集上的對比實驗

COCO 2014 訓練集共包含82 783 張圖像，分為80 個類別。從驗證集中選取5 000 張圖像作為測試集對模型進行評價。COCO 數(shù)據(jù)集將IoU 在［0.5∶0.95］區(qū)間內，步長為0.05 的10 個取值分別計算mAP 并取平均值作為檢測模型的評價結果，相比VOC 數(shù)據(jù)集，COCO 數(shù)據(jù)集的多IoU 評價標準對檢測算法的要求更高，更能反映檢測算法的綜合性能。該組實驗在COCO 2014 數(shù)據(jù)集上的迭代次數(shù)為120 輪，實驗結果如圖10 和表2 所示。可以看出，后3 種模型相對YOLOv3 的檢測效果均有所提高，這得益于BR-IoU-A 損失算法相比L2損失算法對不同尺度邊界框的回歸優(yōu)化更均衡，并且與評價指標IoU 之間的優(yōu)化更加密切，模型BR-YOLO-A 算法的mAP 對 比YOLOv3 提高了1.63 個百分點。此外，由于BR-IoU-B 算法進一步對預測框與真值框之間寬高比的一致性進行優(yōu)化，因此BR-YOLO-B 算法的mAP 比YOLOv3 提高了2.07 個百分點。

圖10 PASCAL VOC 數(shù)據(jù)集上的檢測效果對比Fig.10 Comparison of detection effects on PASCAL VOC data set

表2 COCO 2014 數(shù)據(jù)集上不同算法的mAP 對比Table 2 mAP comparison of different algorithms on COCO 2014 data set %

表3 所示為4 種檢測算法的空間與時間復雜度比較結果，其中時間復雜度為模型檢測每張圖像所需要的時間。由于模型的骨干網(wǎng)絡都為Darknet53，因此4 種算法的網(wǎng)絡參數(shù)數(shù)量基本相同，約為236×106。由表3 可以看出，相比YOLOv3算法，BR-YOLO-A 和BR-YOLO-B 算法檢測速度更快。

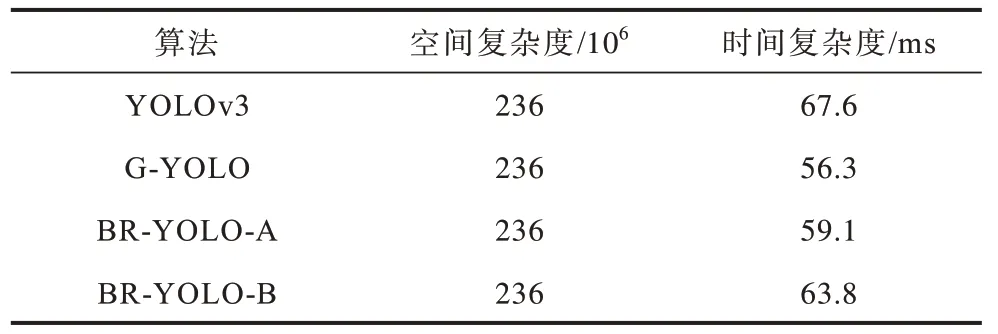
表3 不同算法的時空間復雜度對比Table 3 Time and space complexity comparison of different algorithms

4 結束語

針對YOLOv3 的L2 范數(shù)邊界框回歸損失函數(shù)對邊界框的尺度敏感，以及與算法檢測效果的評價標準IoU 之間相關性不強等問題，本文提出BR-IoU 算法，通過將IoU 作為損失項強化邊界框回歸與算法評估標準的相關性，最小化真值框和預測框中心點形成矩形的面積，同時提高預測框與真值框之間寬高比的一致性，以加強邊界框的回歸收斂性能。實驗結果表明，BR-IoU能夠有效提高YOLOv3 算法的檢測精度和檢測速度。下一步將結合本文算法設計思想對其他目標檢測算法的邊界框回歸損失函數(shù)進行改進，在不影響檢測速度的情況下達到更高的檢測精度。