利用“等和線”解題
2022-03-12 09:44:20鐘建新
數理化解題研究 2022年4期
鐘建新
(浙江省春暉中學 312300)
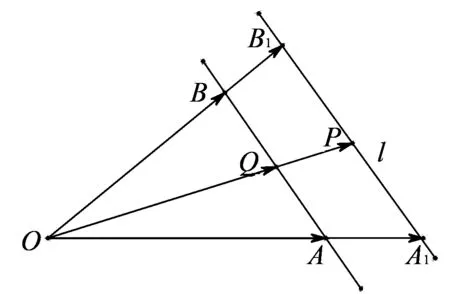
圖1
當等和線恰為直線AB時,k=1;
當等和線在點O和直線AB之間時,k∈(0,1);
當直線AB在點O和等和線之間時,k∈(1,+∞);
當等和線過點O時,k=0;
當等和線與直線AB在點O的兩側時,則k<0.
利用等和線求解數值k(k>0)的基本步驟如下:
①連接AB,構造直線AB;
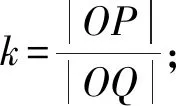
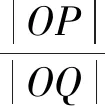
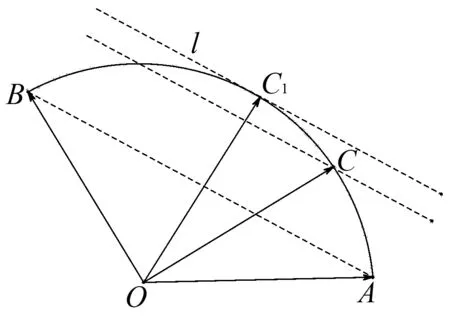
圖2
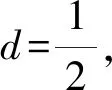
所以由等和線結論得x+y的最大值是2.
例2 在ABCD中,E,F分別為CD和BC的中點,若則x+y=____.
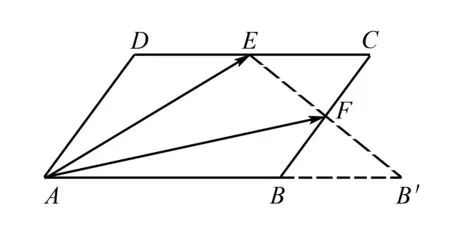
圖3
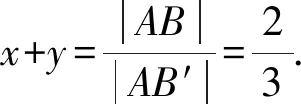
變式在ABCD中,E,F分別為CD和BC的中點,若則x+y=____.
評注若待求和的兩個數不全為題設中基底的兩系數,此時可構造一組新基底,使待求和的兩個數分別為新基底的兩系數.
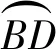
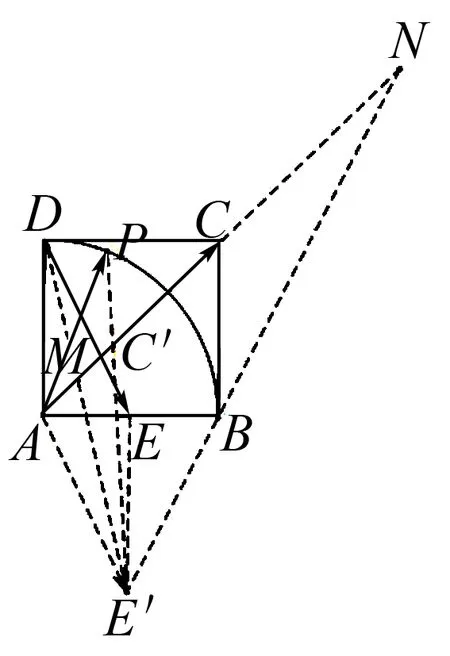
圖4
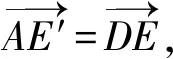
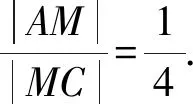
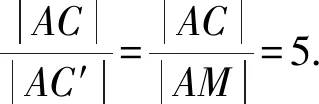
即此時x+y取到最大值5.
當點P運動到點B時,連接CE,易證得CE∥BE′.
因為E為邊AB中點,
所以C為邊AN中點.
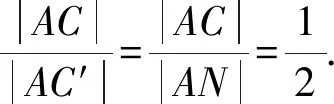
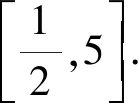
評注等和線所描述的結論要求表達式中的三個向量共起點,若起點不一致,則可考慮利用向量的減法法則或者平移相關向量去統一它們的起點.
G·波利亞在《怎樣解題》指出:“對于一個題目,首先要熟悉題目,我應該從哪里開始?我能做什么?這樣做我能得到什么?然后深入了解題目”.只要我們對相關問題進行全面深入的研究,就會發現其解法還是有跡可循.
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

