注重函數性質交匯 明晰函數圖象判別
黃雅蘭
(廣東省東莞市第一中學 523000)
基本初等函數的性質是高考試題中最為常考的一種題型之一,通過函數圖象去研究函數性質是數學方法中常見的一種研究手段,本文立足函數性質,分析了函數圖象的相關問題.
1 函數性質的綜合應用
例1 已知f(x)是定義在R上的奇函數,且f(x+1)為偶函數,若f(-1)=2,則f(1)+f(2)+f(3)+…+f(2019)=( ).
A.4 B.2 C.0 D.-2
解法1f(x)是定義在R上的奇函數,
所以-f(x)=f(-x).
①
因為f(x+1)為偶函數,
所以f(-x+1)=f(x+1).
②
在②式中,用x+1替代x,
則f(-x)=f(x+2).
所以f(x)=-f(x+2).
③
在①式中,令x+2替代x,
則-f(x+2)=f(-x-2).
④
因為f(-x-2)=f[-(x+3)+1],
再根據②式關系,得
f(-x-2)=f[-(x+3)+1]=f[(x+3)+1]=f(x+4).
綜上所述,得f(x)=f(x+4).
所以f(x)的周期為4.
由已知得,f(x)是定義在R上的奇函數,則
f(0)=0,f(1)=-f(-1)=-2,
f(2)=f(1+1)=f(-1+1)=f(0)=0,
f(3)=f(-1+4)=f(-1)=2,
f(4)=f(0+4)=f(0)=0,
所以f(1)+f(2)+f(3)+f(4)=0.
所以f(1)+f(2)+f(3)+f(4)+…+f(2019)=504×[f(1)+f(2)+f(3)+f(4)]+[f(1)+f(2)+f(3)]=-2+0+2=0.
解法2 由f(x)是定義在R上的奇函數,且f(x+1)為偶函數,可知函數f(x)是周期為4的周期函數.
又f(-1)=2,取f(x)=-2x,x∈[-1,1],
則f(1)=-2,f(2)=f(0)=0,f(3)=f(-1)=2,f(4)=f(0)=0.
所以f(1)+f(2)+f(3)+f(4)+…+f(2019)=504×[f(1)+f(2)+f(3)+f(4)]+[f(1)+f(2)+f(3)]=-2+0+2=0.
點評已知f(x)是周期函數且為偶函數,求函數值常利用奇偶性及周期性進行交換,將所求函數值的自變量轉化到已知解析式的函數定義域內,把未知區間上的函數性質轉化為已知區間上的函數性質求解.
2 函數圖象的識別
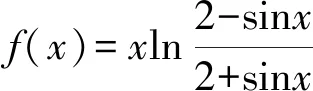

圖1
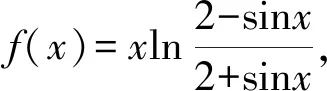
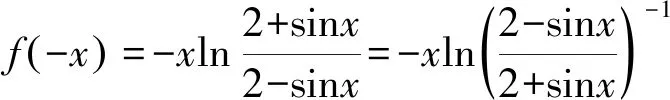
所以f(x)是偶函數.
所以f(x)的圖象關于y軸對稱,故排除C,D.
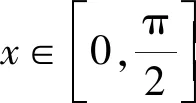
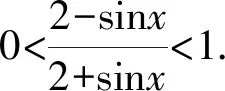
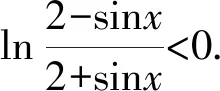
即f(x)<0,故排除B,選A.
例3(2021年廣東湛江模擬)已知函數f(x)的圖象如圖2所示,則f(x)可以為( ).

圖2

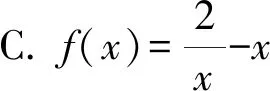
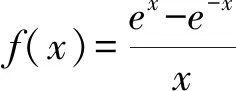
點評函數圖象與解析式之間的4種對應關系:
(1)從函數的定義域判斷圖象的左右位置,從函數的值域(或有界性),判斷圖象的上下位置;
(2)從函數的單調性判斷圖象的升降變化趨勢;
(3)從函數的奇偶性判斷圖象的對稱性:奇函數的圖象關于原點對稱,在對稱的區間上單調性一致,偶函數的圖象關于y軸對稱,在對稱的區間上單調性相反;
(4)從函數的周期性判斷圖象是否具有循環往復特點.
3 函數圖象的變換
例4已知定義在區間[0,4]上的函數y=f(x)的圖象如圖3所示,則y=-f(2-x)的圖象為( ).
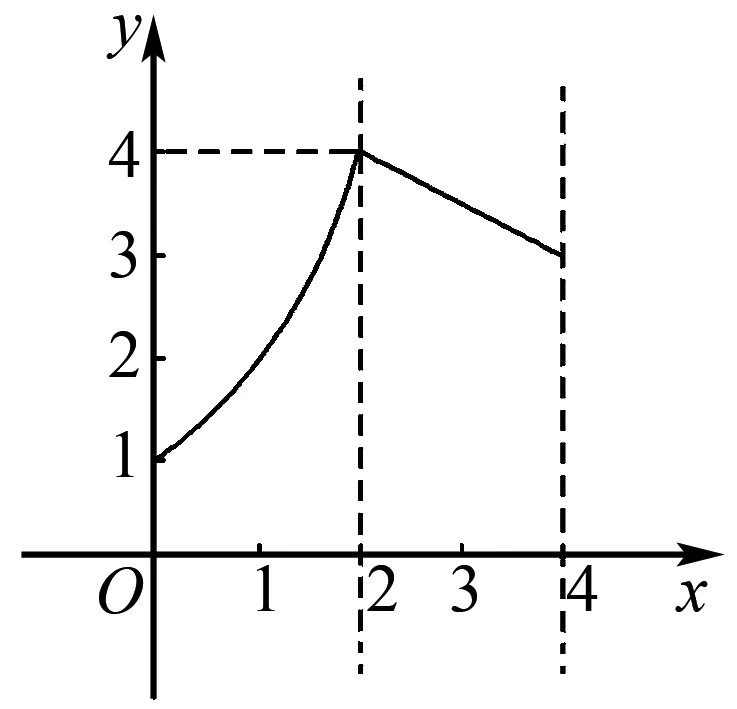
圖3

圖4
解法1先作出函數y=f(x)的圖象關于y軸的對稱圖象,得到y=f(-x)的圖象;然后將y=f(-x)的圖象向右平移2個單位,得到y=f(2-x)的圖象;再作y=f(2-x)的圖象關于x軸的對稱圖象,得到y=-f(2-x)的圖象.故選D.
解法2先作出函數y=f(x)的圖象關于原點的對稱圖象,得到y=-f(-x)的圖象;然后將y=-f(-x)的圖象向右平移2個單位,得到y=-f(2-x)的圖象.故選D.
點評通過圖象變換識別函數圖象要掌握的兩點:
(1)熟悉基本初等函數的圖象(如指數函數、對數函數等函數的圖象);
(2)了解一些常見的變換形式,如平移變換、翻折變換.
4 函數圖象的應用
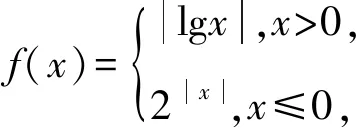
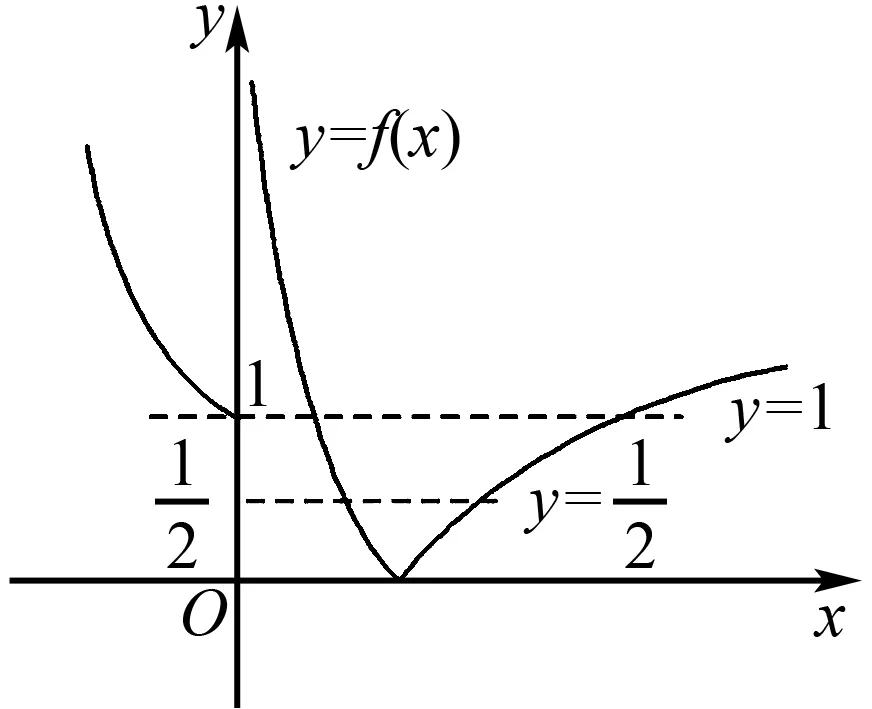
圖5
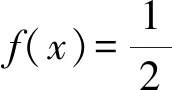
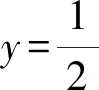
故方程2f2(x)-3f(x)+1=0有5個解.
點評利用函數圖象可以解決很多與函數有關的問題,如利用函數的圖象解決函數性質問題,函數的零點、方程根的問題,有關不等式的問題等,當方程與基本函數有關時,可以通過函數圖象來研究方程的根,方程f(x)=0的根就是函數f(x)圖象與x軸交點的橫坐標,方程f(x)=g(x)的根就是函數f(x)與g(x)圖象交點的橫坐標.

