2021年全國乙卷立體幾何二面角解法賞析
張曉建
(安徽省滁州中學 239000)
1 題目呈現
題目(2021年全國乙卷理科第18題)如圖1,四棱錐P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M為BC的中點,且PB⊥AM.

圖1
(1)求BC;
(2)求二面角A-PM-B的正弦值.
1.1 試題情境分析
本題命制情境的幾何體是一個四棱錐,其滿足底面是一個矩形,有一條側棱垂直于底面,其原型是“陽馬”模型.
1.2 學科核心素養與學業質量水平

學科核心素養學業質量水平(一、二、三)數學思想邏輯推理能夠對與學過的知識有關聯的數學命題的條件與結論的分析,探索論證的思路,選擇合適的論證方法予以證明,并能用準確的數學語言表述論證過程(水平二)直觀想象能夠掌握研究圖形與圖形、圖形與數量之間關系的基本方法,能夠借助圖形性質探索數學規律,解決實際問題或數學問題(水平二)數學運算能夠針對運算問題,合理選擇運算方法、設計運算程序,解決問題.能夠理解運算是一種演繹推理;能夠在綜合運用運算方法解決問題的過程中,體會程序思想的意義和作用(水平二)轉化與化歸
1.3 基礎知識與基本技能
二面角的定義以及二面角的平面角求解;運用向量的方法研究空間基本圖形的位置關系和度量關系,體會向量方法和綜合幾何方法的共性和差異;運用向量方法解決簡單的數學問題和實際問題,感悟向量是研究幾何問題的有效工具;能用向量方法解決點到直線、點到平面、平行直線、平行平面間的距離問題和簡單夾角問題,并能描述解決這一類問題的程序,體會向量方法在研究幾何問題中的作用.
2 解法探究
2.1 第(1)問解析
解析由題知,PD⊥底面ABCD,PD⊥AM.
又PB⊥AM,所以AM⊥平面PDB.
所以AM⊥DB.
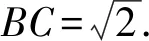
2.2 第(2)問解析

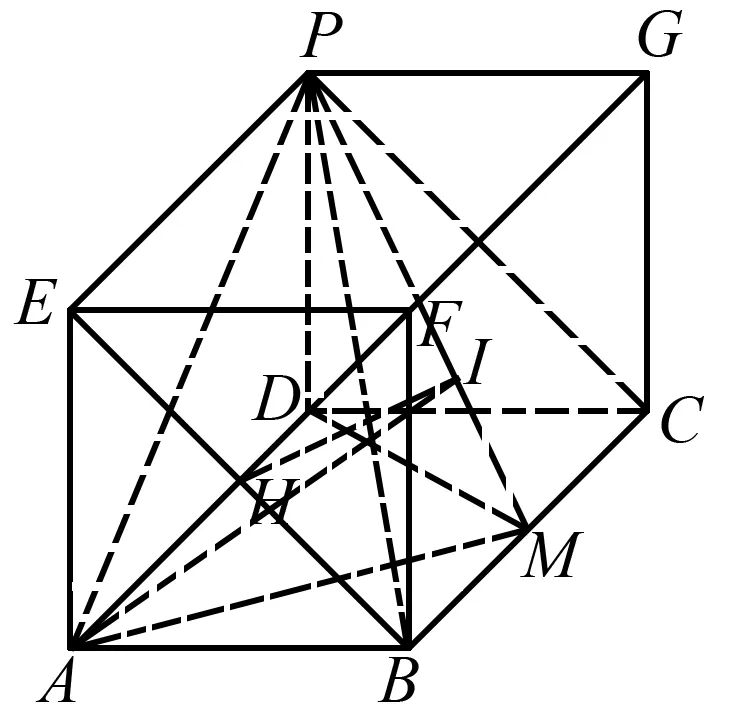
圖2
故平面APM與平面EBCP所成銳二面角即為所求.
連接AF交BE于點H,則由長方體性質可得AH⊥平面EBCP.
過點H作HI⊥PM于點I,連接AI,則∠AIH即為二面角A-PM-B的平面角.

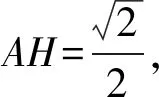
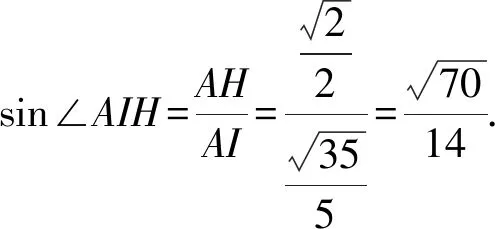
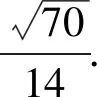

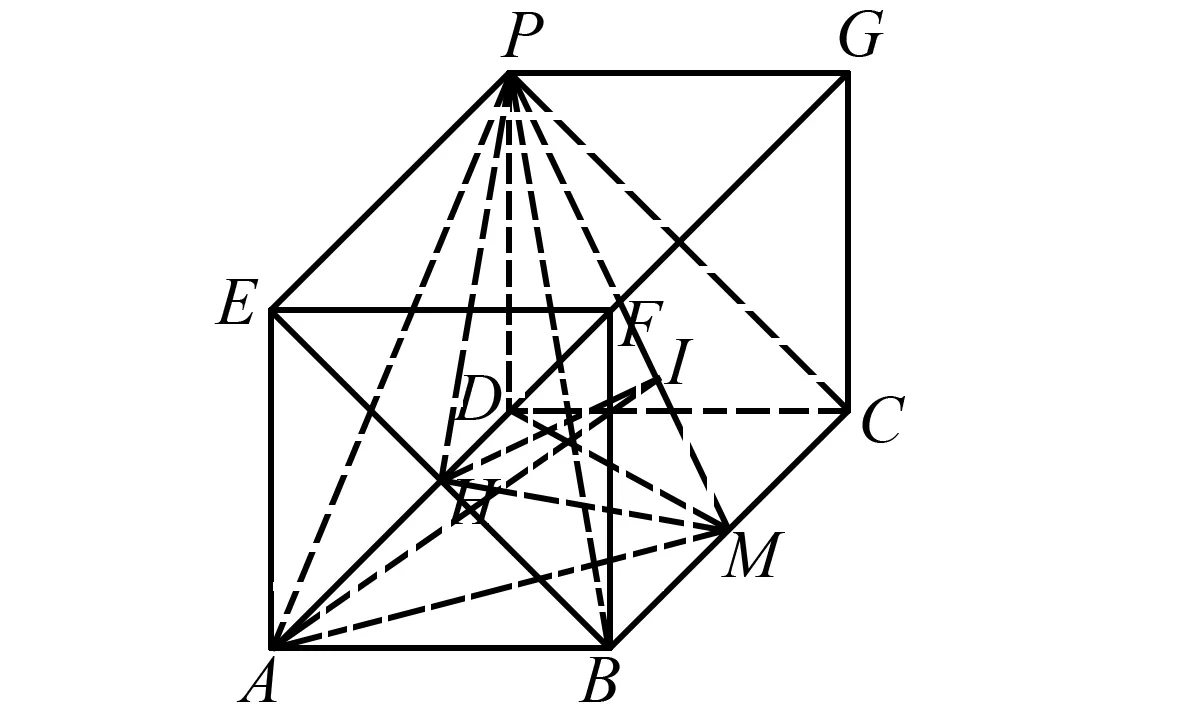
圖3
故平面APM與平面EBCP所成銳二面角即為所求.
連接AF交BE于點H,則由長方體性質可得AH⊥平面EBCP.
過點H作HI⊥PM于點I,連接AI,則∠AIH即為二面角A-PM-B的平面角.





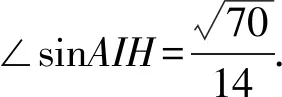
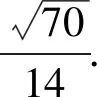
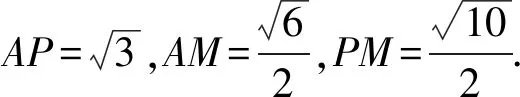
二是建立考核獎勵機制。要進一步健全考核獎勵機制,在檢查評比的基礎上,每年對工作成績突出、群眾認可的協會進行表彰獎勵;對工作不力、群眾意見大的協會進行整頓、改選,確保農民用水戶協會長期發揮效益。
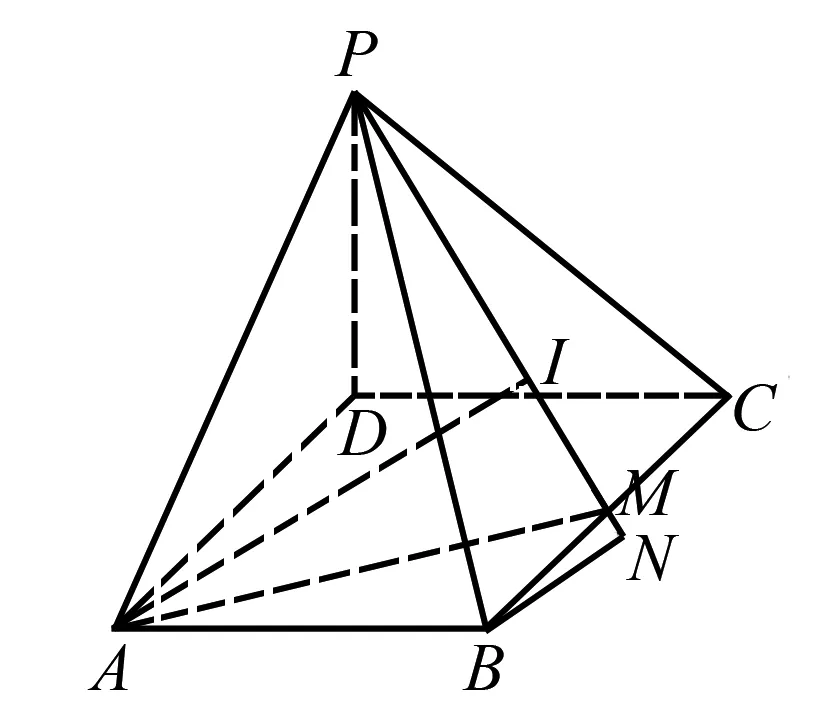
圖4
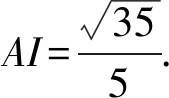

作BN⊥PM于點N,則
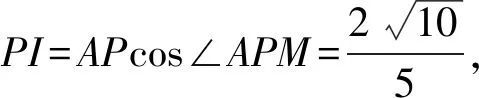
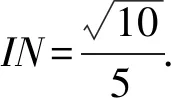



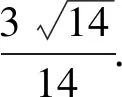
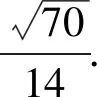
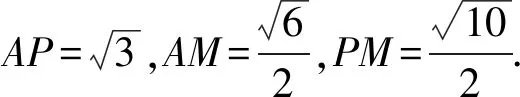

圖5
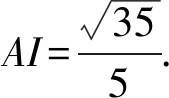
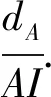
由等體積變換VP-ABC=VA-PBC,

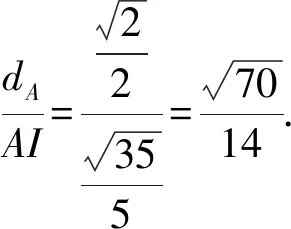
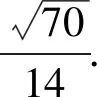
解法5 如圖6,由題意,PD⊥底面ABCD,PD⊥AM.
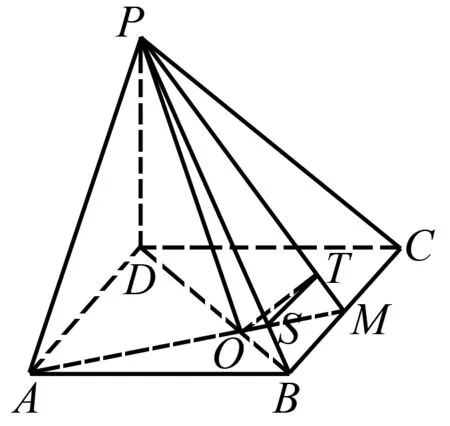
圖6
又PB⊥AM,所以AM⊥平面PDB.
所以平面ABCD⊥平面PDB,且交線為PO.
過點O作OS⊥PO交PB于點S,過點O作OT⊥PM交PM于點T,連接ST,則∠OTS即為二面角A-PM-B的平面角.
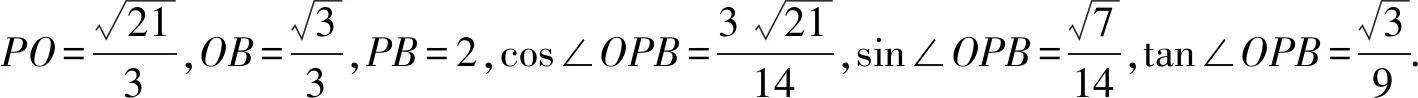

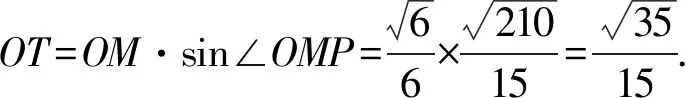
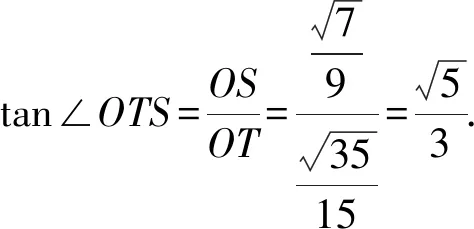

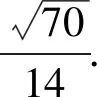
解法6建立如圖7所示空間坐標系D-xyz.

圖7
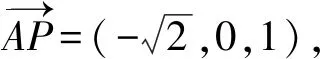
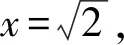
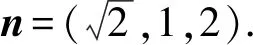
同理可求得平面PMB的一個法向量為m=(0,1,1).

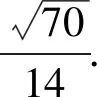
筆者從不同的角度分析、解決二面角的求解問題,當然對于不同的立體幾何模型而言常需要不同的方法,希望能夠借此文章和各位讀者共同探討.為更好地掌握本題,特改編兩道練習如下:
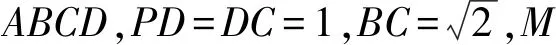

圖8


