基于摩擦因數的齒輪動力學特征仿真分析研究

馮 偉，黃 恒，賀石中

(廣州機械科學研究院有限公司設備狀態檢測研究所，廣東 廣州 510700)

0 引 言

齒輪作為在機械工業設備中必不可少的傳遞運動和動力的通用零件，具有尺寸小、傳動效率高、傳動比準確、壽命長等特點，廣泛應用于各行各業的機械設備中[1]。由于在傳動過程中的關鍵作用，齒輪的運行狀態直接影響整個設備的工作情況，其本身包含了大量的摩擦學和動力學信息[2-3]。針對這些信息進行融合處理，能對設備的故障識別起到重要作用[4-6]。在齒輪副的摩擦學與動力學信息分析中，國內外開展了相關的研究。Chen[7]等分析了中心距變化對間隙的影響，考慮了中心距改變等因素對嚙合剛度的影響。Liu C[8]等研究了人字齒行星齒輪傳動系統的動態特性。LI[9]等建立了齒輪的摩擦動力學模型，證明其對齒輪的疲勞磨損起重要作用。鄒玉靜[10]等建立了斜齒輪摩擦動力學模型并采用解耦方法求解，對齒面摩擦學特性和動力學行為以及兩者之間的耦合關系進行分析。王明凱[11]等建立了雙漸開線齒輪傳動摩擦學和動力學模型，通過分析表明摩擦學與動力學耦合作用對齒輪動力學行為影響較顯著。王奇斌[12]等研究了齒距偏差對直齒輪傳動系統振動特性的影響。

筆者對直齒輪在嚙合過程中的摩擦學特征信息及動力學信息進行相關性分析，通過考慮摩擦因數對齒輪副嚙合動力學仿真特性影響，分析了齒輪副摩擦學與動力學信息之間的耦合關系。

1 齒輪副的摩擦學特征信息

根據對齒輪副相對運動特征的分析，對于兩個齒輪構成的直齒漸開線齒輪傳動系統，在相互嚙合滑動過程中，從動齒輪相對于主動齒輪齒面的滑動方向總是背向節點，壓力沿著齒頂方向而逐漸增大。相對應的，主動齒輪相對于從動齒輪的滑動方向則是朝向節點，而壓力則沿著齒頂方向而逐漸減小[13]。兩齒輪齒廓在嚙合點處線速度的大小和方向均不相同(節點處除外)，則在齒廓間會存在相對滑動，并且相對運動速度的大小與嚙合點的位置有關。由于相對運動的存在，將導致兩齒輪在齒廓之間產生摩擦，從而使得齒面發生磨損。不僅影響齒輪系統的傳動精度和效率，造成齒輪系在工作過程中的振動、噪音以及摩擦發熱，而且隨著磨損的逐漸加劇，會引起齒表的疲勞點蝕與剝落，甚至導致輪齒斷裂。

齒輪副的摩擦學特征信息主要包括兩齒輪在嚙合過程中的摩擦力的變化特征信息，主要包括摩擦力的大小與方向兩個方面。圖1所示為齒輪嚙合過程中齒面摩擦力的方向。主動輪所受摩擦力的方向背離節線，而從動輪所受摩擦力的方向則是朝向節線。若潤滑不良，則有可能造成齒面材料塑性變形或者流動，引起摩擦因數的改變，從而造成齒面磨損。

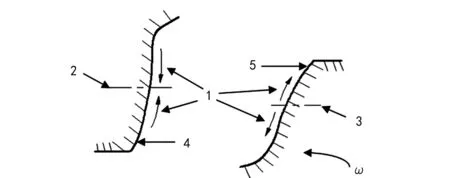
圖1 齒輪副摩擦力方向示意圖1.摩擦力方向 2，3.節線 4.從動齒輪2齒表 5.主動齒輪1齒表

2 齒輪副的動力學特征

齒輪副作為一個振動系統，根據傳動特點，一對直齒圓柱齒輪扭振物理模型可以簡化為如圖2所示。

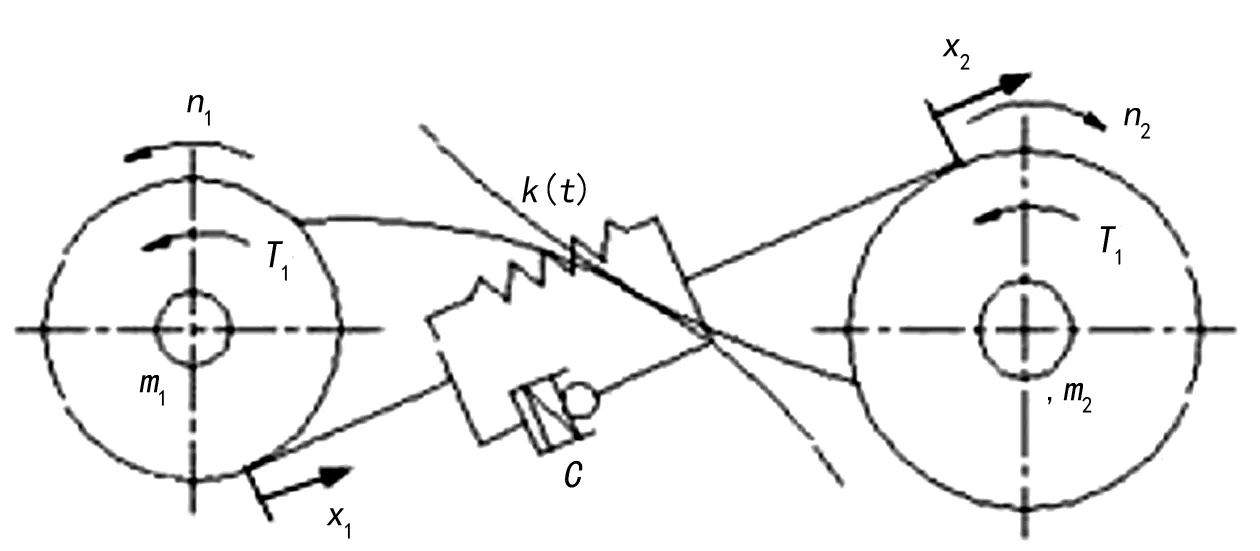
圖2 齒輪傳動扭振物理模型

圖中2為主動輪，2為從動輪，n1、n2為主、被動齒輪的轉速。根據振動理論，齒輪副動力學方程可以寫成如下公式：

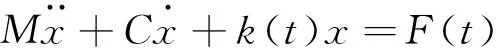
(1)

式中：M為齒輪當量質量，M=(m1m2)/(m1+m2)；x為嚙合線上齒輪相對位移；C為齒輪嚙合阻尼；k(t)為齒輪嚙合剛度；F(t)為動載荷，包含齒表故障缺陷產生的動態激勵，受輪齒嚙合剛度、傳動誤差和齒面摩擦力方向等因素影響。如果忽略齒輪之間的摩擦力不計，方程(1)可以寫為：

(2)

式中：E1為齒輪在載荷作用下的平均靜彈性變形；E2(t)稱為故障函數，表示齒輪的誤差和故障造成的兩個齒輪間的相對位移。

齒輪故障函數E2(t)由兩部分組成，一部分為嚙合誤差，另一部分為旋轉誤差。齒輪誤差函數可以寫為：

(3)

式中：A為齒輪旋轉誤差的幅值；Bn為齒輪嚙合誤差的幅值；φn齒輪嚙合誤差相位；ωr為齒輪旋轉角速度；ωk為齒輪嚙合角速度。

齒輪嚙合剛度k(t)的變化是齒輪系統振動的重要激振源之一，它是一個周期性的變量，隨著齒輪嚙合點位置和參加嚙合的齒數的變化而變化。設t=0時為齒輪副處于雙嚙合狀態，將k(t)展開為Fourier級數得：

(4)

式中：Ck為齒輪嚙合剛度諧波；φn′為齒輪嚙合剛度諧波相位。

3 變摩擦因數的齒輪動力學特征信息仿真研究

針對以上對齒輪副的摩擦學和動力學的特征信息分析研究，為了進一步了解摩擦學信息對動力學信息的影響規律，文中使用ADMAS軟件進行仿真，分析兩者之間的影響。采用如圖3所示的常規汽車變速箱的3檔齒輪系進行嚙合建模。

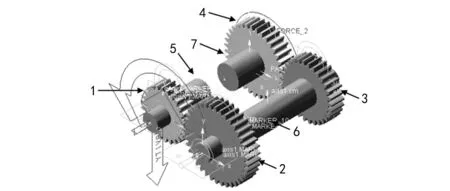
圖3 齒輪系仿真物理模型1.齒輪1 2.齒輪2 3.齒輪3 4.齒輪4 5.輸入軸 6.中間軸 7.輸出軸

模型中的各結構參數如下：齒輪1的齒數為z1=26，齒輪2的齒數為z2=38，齒輪3的齒數為z3=30，輸出軸上齒輪4的齒數為z4=35，模數m=3.75 mm，齒寬b=30 mm。設置各齒輪的質量及轉動慣量為：m1=1.729 kg；m2=3.721 kg；m3=2.309 kg；m4=3.153 kg；I1=2.064·10-3kg·m2，I2=9.448·10-3kg·m2，I3=3.663·10-3kg·m2，I4=6.795·10-3kg·m2。在使用ADAMS仿真計算時，設置齒輪1、2之間的重合度ε1=1.662 1，齒輪3、4之間的重合度ε2=1.670 1，彈性模型e=206 GPa，泊松比r=0.3。節點嚙合處單齒對嚙合剛度為kd1=2.16×108N/m,kd2=2.19×108N/m，雙齒對嚙合平均剛度為ks1=3.23×108N/m，ks2=3.29×108N/m。力指數取值為2.2，阻尼系數為10 N·s/mm；阻尼力過渡區間取0.1 mm；靜態阻力滑移速度取0.1 m/s；動態阻力轉化速度取1.0 m/s。

3.1 速度分析

首先通過仿真計算分析齒輪系運動過程中達到動平衡時角速度大小隨摩擦因數變化的關系。在主動輪1所在的輸入軸上分步施加主動轉矩250 N·m，從動輪4所在的輸出軸上同步施加負載轉矩為200 N·m。步長取0.000 1 s，仿真時間為10 s。考慮到齒面間摩擦力的影響，取靜摩擦因數為0.3，動摩擦因數則取值μ1=0.05，μ2=0.10，μ3=0.15。所得到的關系變化如圖4所示。

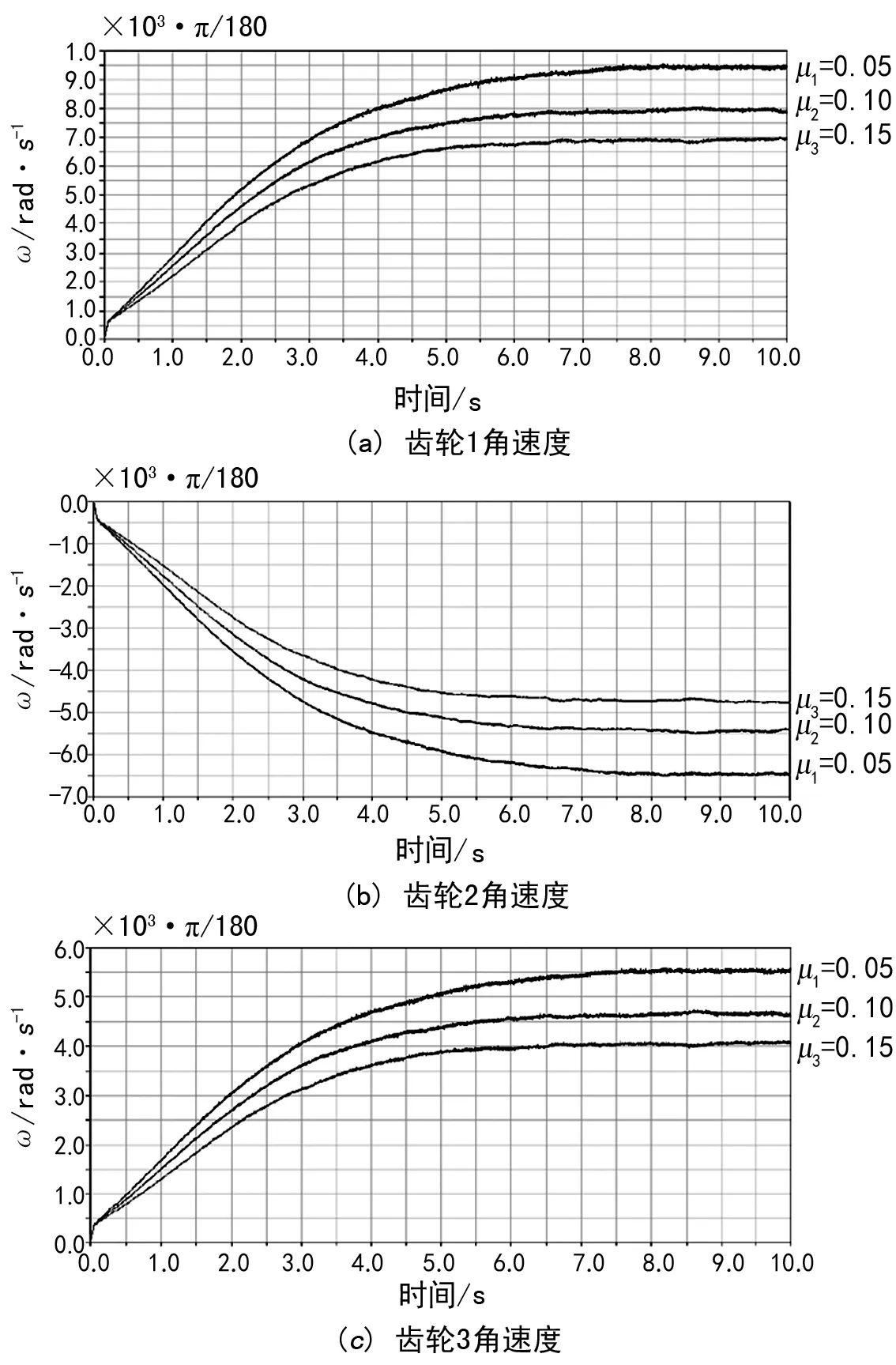
圖4 齒輪角速度隨摩擦因數變化曲線圖

從圖中可以看出，在啟動初期，齒輪副受到的啟動轉矩較大，從而造成轉速迅速增大。隨著時間繼續增加，在8s前，轉速也隨著轉矩的增 加而相應增大。并且在整個過程中，隨著摩擦因數的增大，各級齒輪的轉速是減小的。而在8 s后，齒輪系的運動逐漸達到了平衡狀態，轉速保持恒定，這個平衡狀態是動態的。對8 s后的曲線變化進行觀察可知，各齒輪的轉速是在一定范圍內進行周期性波動，截取圖1中μ1=0.05，8 s后的轉速變化曲線進行放大如圖5所示。

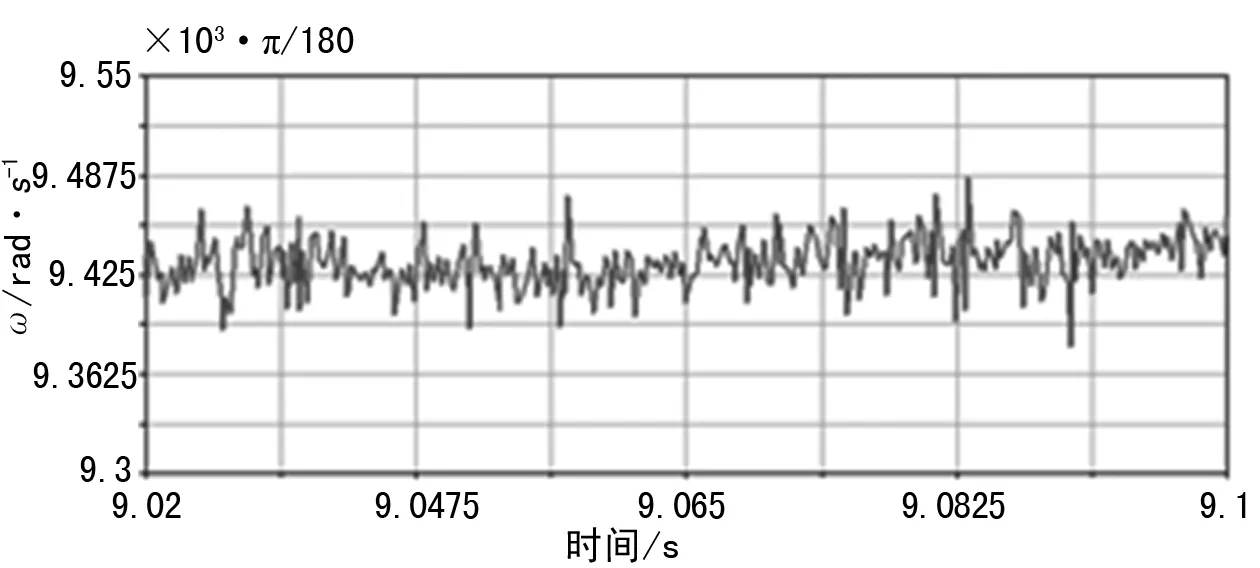
圖5 平衡時齒輪1角速度變化曲線

圖5可看出，齒輪的轉速在一定范圍內發生周期性波動，這主要是齒輪在傳動過程中的振動與嚙合沖擊導致的。對于μ1=0.05的情況，在ADAMS軟件中對齒輪在8 s后的轉速計算平均值分別為164.5 rad/s,112.6 rad/s,96.5 rad/s，所得到的轉速比符合傳動比的要求。

3.2 嚙合力仿真分析

其次針對齒輪系在不同摩擦因數條件下嚙合力的變化情況。設置仿真條件為：輸入功率為42 kW，在輸入軸上施加轉速為167.5 rad/s的驅動，并且在ADAMS中接觸力step函數中設定在0.2 s內轉速由0增加至167.5 rad/s。從動齒輪4所在的輸出軸在0.05 s后施加一個大小為200 N·m的恒定轉矩。仿真時間根據多次仿真試計算取0.3 s達到平衡，計算步長取0.000 1 s。考慮齒面間摩擦力的影響，取靜摩擦因數為0.3，動摩擦因數選取齒輪系處于邊界潤滑狀態下的值μ2=0.10。對0.3 s時間范圍內齒輪系的轉速變化情況進行仿真，所得結果如圖6所示。

從圖6中可以看出，在0.2 s前，各級齒輪的轉速變化較為明顯。在0.2 s后，運動達到平衡狀態，輸入端齒輪1的轉速約為166.0 rad/s，中間軸齒輪2、3的轉速約為-114.52 rad/s，輸出端齒輪4的轉速約為98.3 rad/s。通過計算可得，各級齒輪的轉速與傳動比的要求一致。

對齒輪系輸入端與輸出端嚙合力作出時域和頻域圖，由于是在0.05 s后開始施加負載，故在0.05 s后才開始產生嚙合力。如圖7是輸入端齒輪副嚙合力的時域圖和頻域圖，圖8是輸出端齒輪副嚙合力的時域圖和頻域圖。

圖6 齒輪轉速變化曲線圖

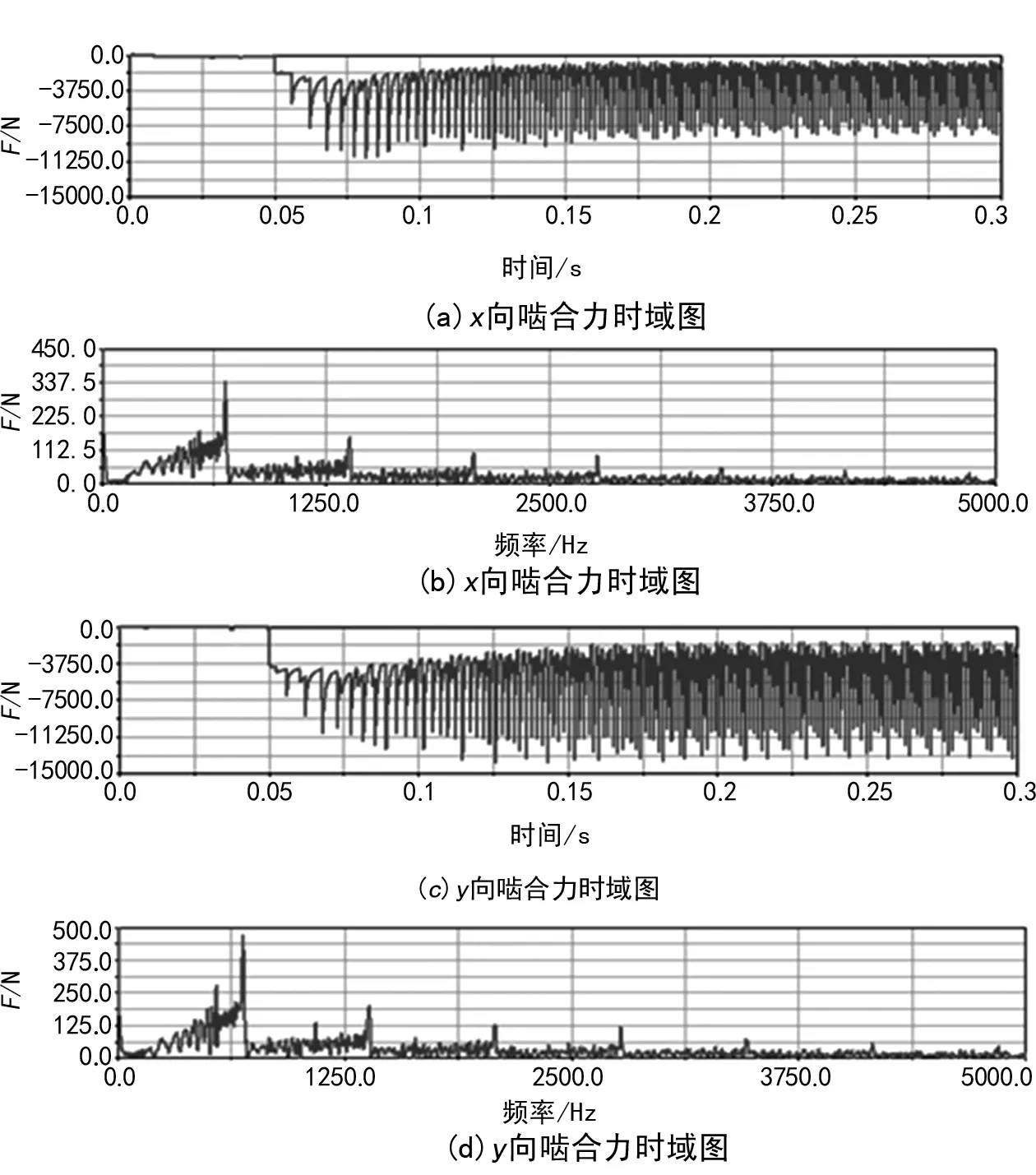
圖7 輸入端齒輪副嚙合力時域頻域圖

從圖8中可以看出，在0.005 s后，隨著負載的增加，嚙合力也開始增加，齒輪就有一定的初速度，并且在很短時間內產生一個較多的沖擊。根據齒輪嚙合運動的特點，在開始階段，x向分力(徑向力)逐漸增大，因此在圖8(a)中表現為嚙合力有一個很大的值。在0～0.2 s的過程中，徑向力的周期由大變小，幅值也逐漸減小；在0.2 s后，波動趨于穩定。而對于y向分力(圓周力)，在0～0.2 s階段，嚙合力的周期由大變小，并且力的大小逐漸增加。在0.2 s后，波動趨于穩定。根據齒輪嚙合過程中徑向力和圓周力的理論計算公式，將算得的理論值與仿真值進行比較如表1所列。從表中可以看出，理論值與仿真值較為接近，證明仿真結果是準確的。

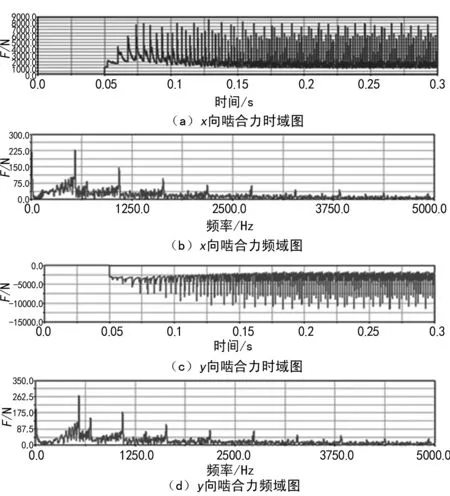
圖8 輸出端齒輪副嚙合力時域頻域圖

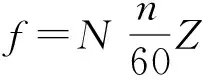
表1 嚙合力數值比較

對齒輪系在不同摩擦因數的條件下，達到平衡轉動時的嚙合力進行仿真。如圖9為齒輪在達到平衡時嚙合力的曲線。從圖中可以看出，軸向力和徑向力都會隨著齒面摩擦因數的變化而發生變化。摩擦因數越大，齒面的嚙合力則相應增加。這主要是因為齒面摩擦力的方向與兩齒面相對滑動速度方向相反，嚙合力的大小受到摩擦因數的影響。

從圖中分析可知，對于不同摩擦因數的嚙合力曲線，x向嚙合力偏差很小，而y向嚙合力幾乎重合。這說明在仿真過程中，由于齒面間磨損造成的能量損失較小，幾乎可以忽略不計。而在實際嚙合過程中，摩擦力所造成的摩擦損失往往會增加能量耗損，影響齒面的接觸特性，從而使齒面的接觸力變大。

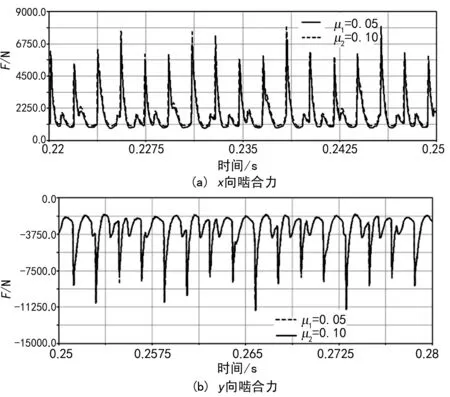
圖9 輸出端齒輪嚙合力

5 結 論

通過對齒輪系摩擦學特征信息和動力學特征信息進行理論計算與分析，研究了兩者之間的相關性，并通過ADMAS對齒輪系的動力學特征進行仿真。得到以下結論。

(1) 齒輪系的摩擦學特征信息與動力學特征信息之間存在著相關性，兩者之間的特征能夠對齒輪系的故障類型識別等提供基礎。

(2) 齒輪嚙合過程中的仿真結果表明，齒輪嚙合力的仿真值與理論值之間的差值在誤差范圍內，并且在不同摩擦因數條件下嚙合力的大小稍微發生變化，與理論計算基本一致。

(3) 通過仿真分析齒輪系摩擦磨損信息對振動的影響表明，齒輪摩擦學信息與動力學信息之間相互影響、相互滲透，在輸出狀態特征過程中表現出較強的耦合性。