輸入受限下欠驅(qū)動AUV軌跡跟蹤滑模控制

李鑫濱, 王 鵬, 駱 曦, 潘洪濤

輸入受限下欠驅(qū)動AUV軌跡跟蹤滑模控制

李鑫濱, 王 鵬, 駱 曦, 潘洪濤

(燕山大學(xué) 智能控制系統(tǒng)與智能裝備教育部工程研究中心, 河北 秦皇島, 066004)

針對欠驅(qū)動自主水下航行器(AUV)在外界干擾和輸入受限下水平面軌跡跟蹤問題, 提出了基于非線性干擾觀測器和徑向基函數(shù)(RBF)神經(jīng)網(wǎng)絡(luò)的滑模控制器。首先, 將欠驅(qū)動AUV運動學(xué)模型通過坐標(biāo)變換轉(zhuǎn)換為誤差運動學(xué)模型鎮(zhèn)定位置誤差; 其次, 利用反步法設(shè)計艏搖角虛速度控制律, 鎮(zhèn)定姿態(tài)誤差; 然后采用非線性干擾觀測器對時變海流擾動進行估計, 并通過濾波器估計虛擬控制律的導(dǎo)數(shù), 避免了虛擬控制律求導(dǎo)引起的“微分爆炸”; 最后, 設(shè)計自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)對欠驅(qū)動AUV實際輸入進行補償, 通過李雅普諾夫穩(wěn)定性證明閉環(huán)跟蹤誤差所用信號一致有界。仿真驗證了所設(shè)計控制器的有效性。

欠驅(qū)動自主水下航行器; 輸入受限; 軌跡跟蹤; 滑模控制

0 引言

隨著人類科學(xué)技術(shù)的不斷進步, 人們對海洋資源的開發(fā)和投入也隨之增大。欠驅(qū)動自主水下航行器(autonomous undersea vehicle, AUV)由于具有更高的機動性和系統(tǒng)可靠性, 在海洋科學(xué)調(diào)查、水下勘探和海洋目標(biāo)探查等領(lǐng)域中起到了重要作用[1-2]。實現(xiàn)AUV控制系統(tǒng)穩(wěn)定的軌跡跟蹤是確保其在水下平穩(wěn)可靠工作的關(guān)鍵。但在實現(xiàn)精確而魯棒的動態(tài)控制時, 通常會遇到2個問題: 一是如何在復(fù)雜未知外部干擾的情況下提高系統(tǒng)的魯棒性[3], 這些外部干擾會嚴(yán)重降低閉環(huán)系統(tǒng)的性能; 二是如何解決執(zhí)行器幅值問題導(dǎo)致控制效果下降甚至不穩(wěn)定的問題[4]。

近年來, 模糊控制方法、滑模控制方法、反步控制方法、自適應(yīng)控制方法和神經(jīng)網(wǎng)絡(luò)法等魯棒控制方法被廣泛用于AUV的運動控制中。Liang等[5]針對AUV在模型不確定性和時變干擾等復(fù)雜未知條件下軌跡跟蹤問題, 提出一種自適應(yīng)模糊動態(tài)面控制器(dynamic surface control, DSC)。鄧非等[6]針對AUV存在洋流干擾、非線性等問題, 提出了一種基于高增益觀測器的反步控制。Wang等[7]針對AUV復(fù)雜非線性問題, 提出了一種基于神經(jīng)網(wǎng)絡(luò)的自適應(yīng)控制器, 但未考慮能耗和續(xù)航問題。Che等[8]考慮到在舵機故障和洋流干擾下的AUV控制問題, 提出了基于神經(jīng)網(wǎng)絡(luò)估計器的容錯控制, 使閉環(huán)系統(tǒng)具有良好性能。Cho等[9]針對AUV跟蹤控制問題, 提出了基于誤差動力學(xué)的反步控制, 但是未考慮虛擬控制律“微分爆炸”問題。

此外, 由于AUV機載執(zhí)行器的物理限制, 幾乎所有的執(zhí)行器都會受到輸入非線性的影響, 控制輸入受限是實際姿態(tài)控制系統(tǒng)的主要控制問題之一, 這可能導(dǎo)致控制效果下降甚至不穩(wěn)定。Xia 等[10]針對AUV執(zhí)行器飽和問題, 提出了基于抗飽和補償器的滑模控制。Sarhadi等[11]提出了基于積分狀態(tài)反饋的自適應(yīng)控制器, 通過在積分狀態(tài)反饋基礎(chǔ)上加入抗飽和(anti-windup)補償器解決AUV執(zhí)行器受限中的飽和問題, 但設(shè)計過程復(fù)雜且未考慮外界擾動對系統(tǒng)穩(wěn)定性的影響。Yu等[12]提出了自適應(yīng)模糊控制的方法, 主要思想是將深度跟蹤誤差轉(zhuǎn)化為仰角跟蹤誤差, 解決了升沉?xí)r的欠驅(qū)動結(jié)構(gòu)問題。在控制回路中, 采用直接自適應(yīng)模糊控制來補償執(zhí)行器受限的影響。江夢潔等[13]提出了一種基于觀測器的控制器, 在軌跡跟蹤誤差方程基礎(chǔ)上, 設(shè)計了一種誤差信號觀測器對原有跟蹤誤差進行近似, 通過引入一種光滑有界函數(shù)作為輸入飽和條件的近似, 以及一種Nussbaum型偶函數(shù), 設(shè)計了飽和動力學(xué)控制器實現(xiàn)執(zhí)行器受限下AUV穩(wěn)定控制。楊立平等[14]針對AUV推力飽和時控制器控制性能下降問題, 設(shè)計了一種基于抗積分飽和控制的主動容錯控制方法。

基于上述文獻分析, 文中進一步研究了在執(zhí)行器幅值受限下欠驅(qū)動AUV的魯棒控制。首先, 通過坐標(biāo)變換, 將欠驅(qū)動AUV的模型轉(zhuǎn)換為極坐標(biāo)系下的誤差模型, 將位置誤差的鎮(zhèn)定轉(zhuǎn)換為視線誤差的鎮(zhèn)定。進一步, 針對動力學(xué)控制系統(tǒng), 引入非線性干擾觀測器對時變海流擾動進行估計。同時, 通過濾波器估計由反步法設(shè)計速度虛擬控制律的導(dǎo)數(shù), 防止“微分爆炸”。針對執(zhí)行器幅值未知設(shè)計自適應(yīng)徑向基函數(shù)(radial basis function, RBF)神經(jīng)網(wǎng)絡(luò)進行補償, 通過Lyapunov穩(wěn)定性理論分析閉環(huán)系統(tǒng)的穩(wěn)定性, 證明跟蹤誤差的有界穩(wěn)定, 通過仿真對比驗證所提控制器的有效性。

該文的主要貢獻體現(xiàn)在以下幾方面:

1) 通過采用非線性干擾觀測器對時變海流擾動進行估計, 降低了由擾動引起的滑模控制器抖振;

2) 利用反步法設(shè)計艏搖角速度虛擬控制律, 并采用濾波器求解虛擬控制律的導(dǎo)數(shù), 避免了虛擬控制律求導(dǎo)引起的“微分爆炸”;

3) 設(shè)計自適應(yīng)RBF神經(jīng)網(wǎng)絡(luò)滑模控制器, 基于穩(wěn)定性理論構(gòu)建自適應(yīng)律并通過反饋回路對執(zhí)行器實際輸入偏差進行補償, 解決了輸入受限問題。

1 欠驅(qū)動AUV模型

欠驅(qū)動系統(tǒng)是指獨立控制輸入少于系統(tǒng)自由度的一類非線性系統(tǒng)。欠驅(qū)動AUV因其質(zhì)量輕、慣性小、系統(tǒng)成本低且其驅(qū)動受多驅(qū)動裝置協(xié)同作用具有較高容錯率等優(yōu)點受到國內(nèi)外廣泛關(guān)注[15]。欠驅(qū)動系統(tǒng)往往伴隨著高度耦合和非線性等問題, 使得對欠驅(qū)動AUV的軌跡跟蹤具有一定難度和局限性。欠驅(qū)動AUV在水平面不能完成水平橫移和橫滾運動[16]。

使用體坐標(biāo)系和慣性坐標(biāo)系描述欠驅(qū)動AUV水平面軌跡跟蹤(見圖1), 可將其描述為運動學(xué)模型和動力學(xué)模型。

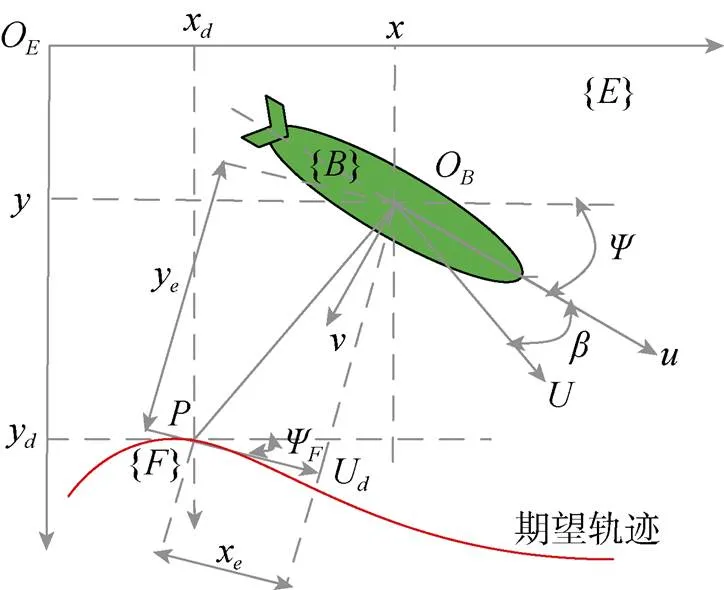
圖1 水平面軌跡跟蹤示意圖

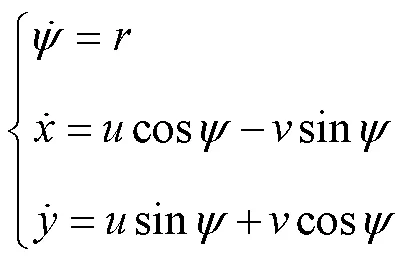
根據(jù)牛頓-歐拉方程和拉格朗日方程推導(dǎo), 欠驅(qū)動AUV動力學(xué)模型可以描述[10]為

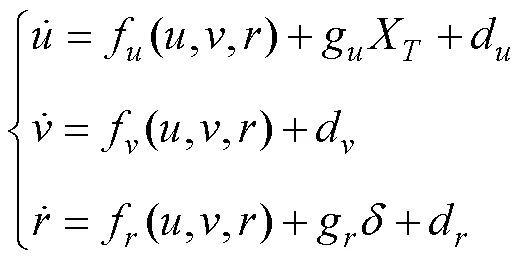
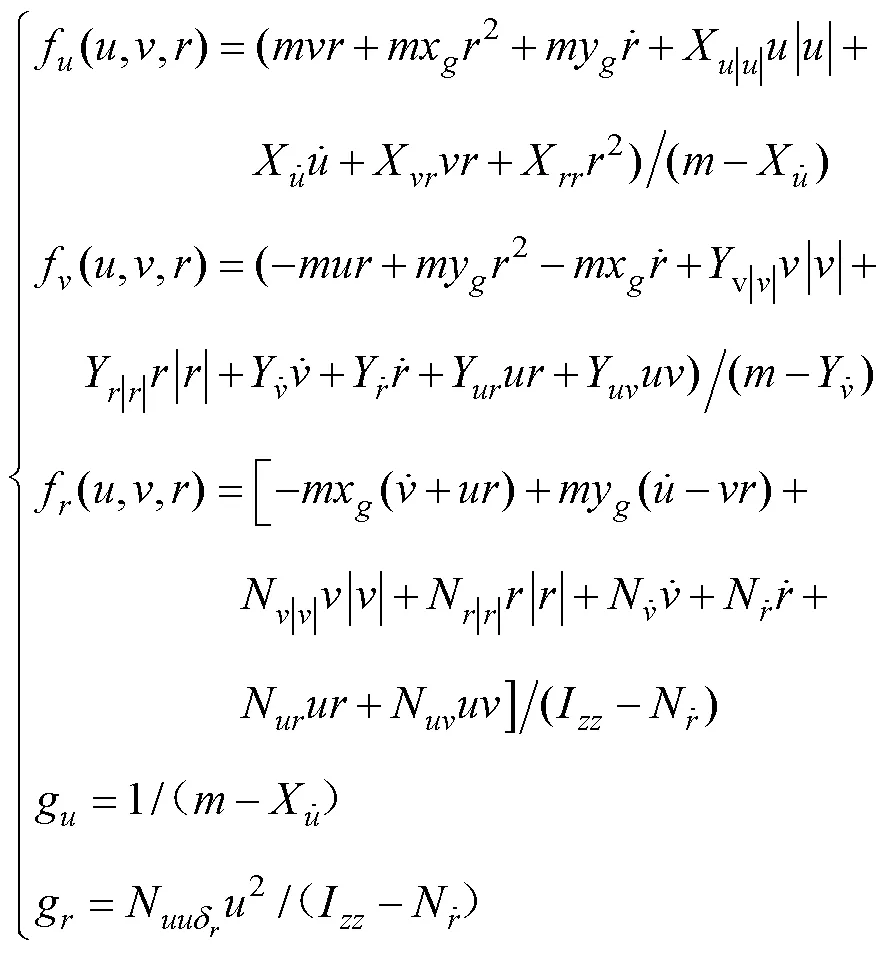
為了便于控制器設(shè)計, 做出如下假設(shè):

1) 所有給定參考信號有界且可導(dǎo), 并且其導(dǎo)數(shù)也有界。

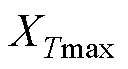
2 欠驅(qū)動AUV跟蹤控制器設(shè)計

在控制器設(shè)計中充分考慮洋流擾動和執(zhí)行器輸入受限對系統(tǒng)穩(wěn)定的影響, 分別針對運動學(xué)模型和動力學(xué)模型設(shè)計控制器, 控制器的設(shè)計如圖2所示。采用基于視線制導(dǎo)律和虛速度的控制策略, 首先, 通過慣性坐標(biāo)系下位置和姿態(tài)誤差轉(zhuǎn)換為體坐標(biāo)系下的位置和姿態(tài)誤差, 設(shè)計視線制導(dǎo)律鎮(zhèn)定位置誤差, 虛速度鎮(zhèn)定欠驅(qū)動AUV的姿態(tài)誤差, 并用虛速度作為AUV的期望速度設(shè)計控制器, 采用濾波器對設(shè)計的虛速度進行濾波處理, 解決“微分爆炸”; 再設(shè)計干擾觀測器對時變的洋流擾動進行估計, 然后基于RBF神經(jīng)網(wǎng)絡(luò)和積分滑模控制方法設(shè)計動力學(xué)控制律, 使AUV的速度達到期望值, 最后, 使欠驅(qū)動AUV跟蹤上期望軌跡, 并且滿足系統(tǒng)穩(wěn)定。

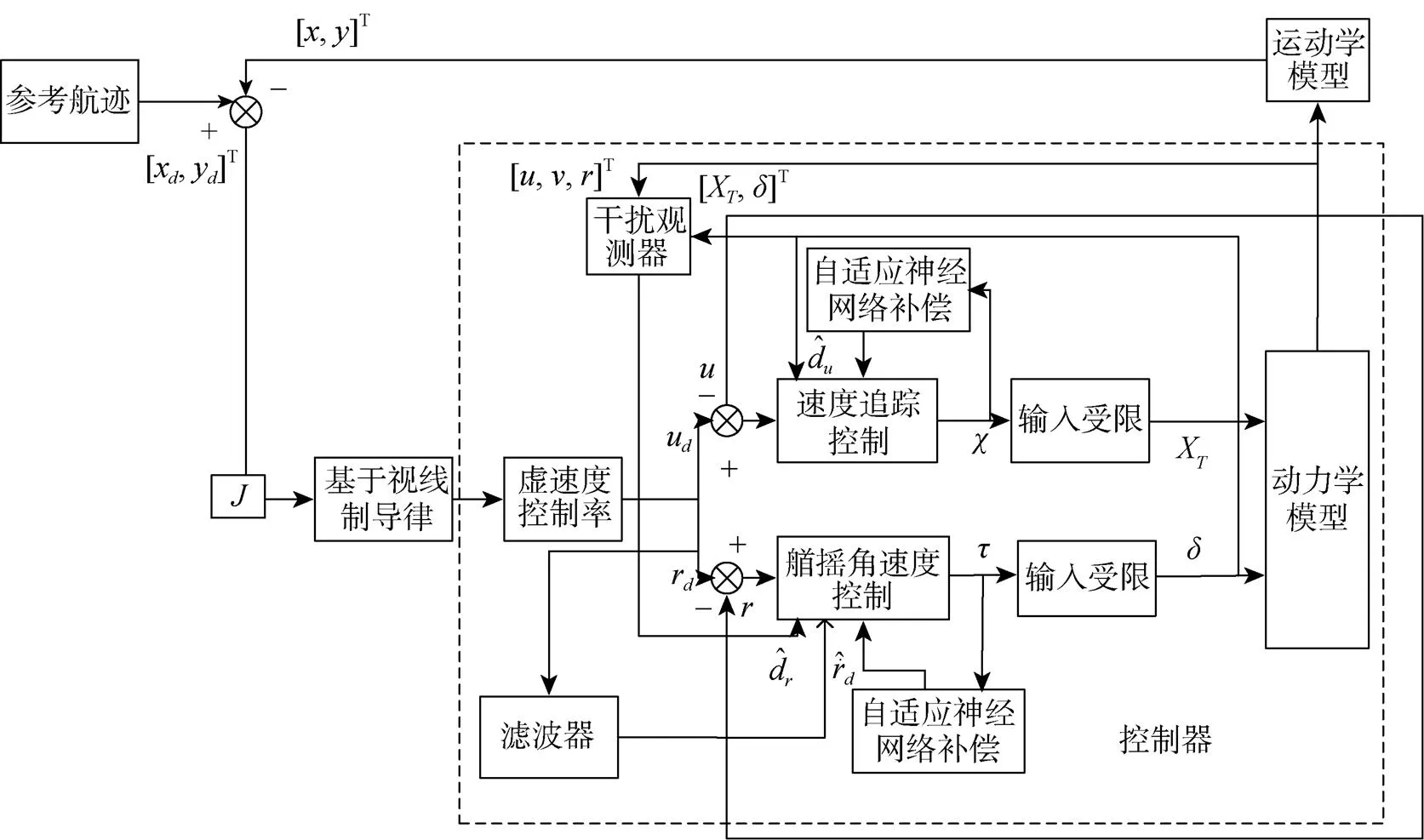
圖2 欠驅(qū)動AUV仿真控制系統(tǒng)框圖

2.1 運動學(xué)控制律設(shè)計

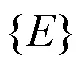
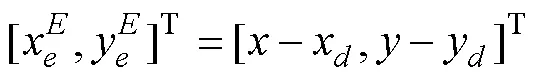
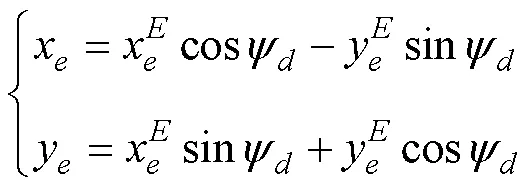
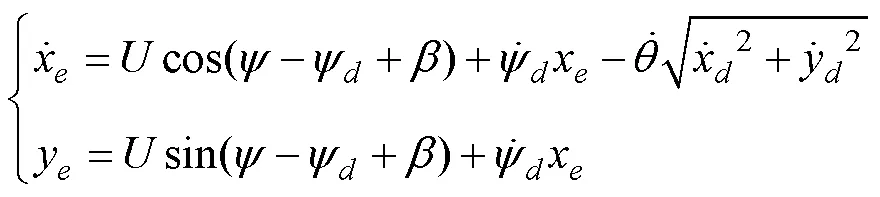
構(gòu)造Lyapunov函數(shù)

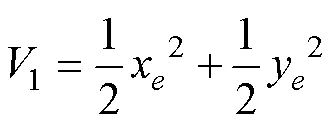
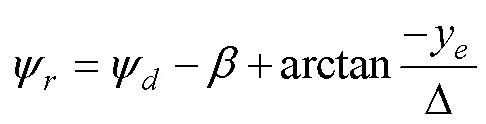
設(shè)計虛擬控制律

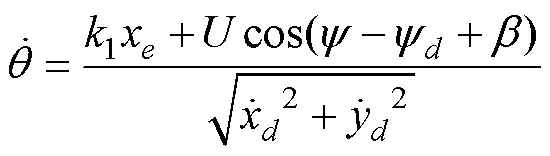
將所設(shè)計的制導(dǎo)律代入式(8)可得

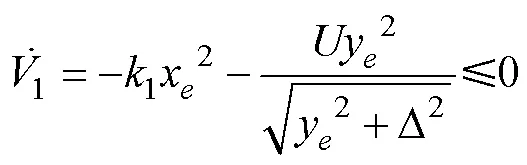
定義艏搖角度誤差為

構(gòu)造Lyapunov函數(shù)

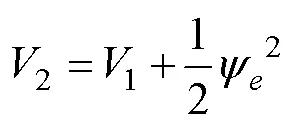
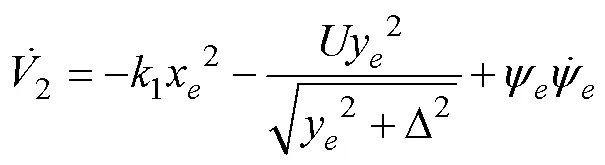
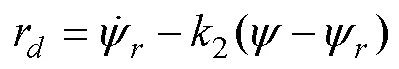
式中,2為大于0的待設(shè)計參數(shù)。

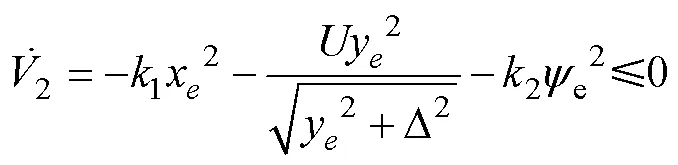
2.2 動力學(xué)控制律設(shè)計

在運動學(xué)控制中, 由艏搖角制導(dǎo)律和艏搖角虛速度控制律通過鎮(zhèn)定位置誤差和姿態(tài)誤差, 使欠驅(qū)動AUV跟蹤期望軌跡。但是速度變量不能直接控制, 需要動力學(xué)控制器驅(qū)動AUV才能跟蹤上期望速度, 因此, 將分別針對洋流和輸入受限下動力模型設(shè)計艏搖角速度跟蹤控制器和浪涌速度跟蹤控制器, 通過引入干擾觀測器對外界干擾進行估計, 針對執(zhí)行器幅值未知設(shè)計自適應(yīng)神經(jīng)網(wǎng)絡(luò)滑模控制器。

1) 艏搖角速度跟蹤控制

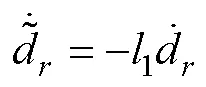
考慮到AUV易受到水下溫度、壓力等環(huán)境因素的影響, 會使系統(tǒng)某些參數(shù)改變而出現(xiàn)幅值未知的情況, 致使未知。通過設(shè)計自適應(yīng)神經(jīng)網(wǎng)絡(luò)滑模控制器, 實現(xiàn)對執(zhí)行器輸入受限下的欠驅(qū)動AUV控制。其閉環(huán)示意圖如圖3所示。

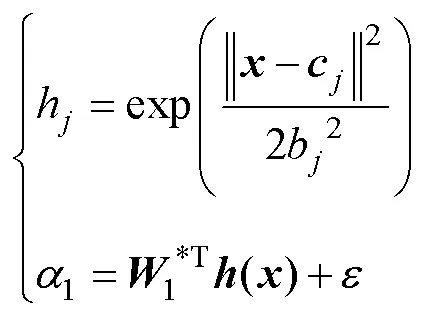
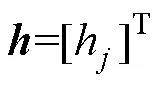
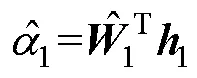
定義艏搖角速度跟蹤誤差為

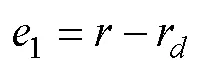
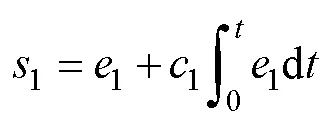
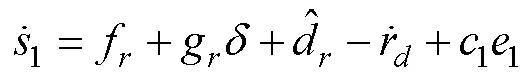
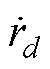
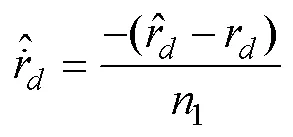
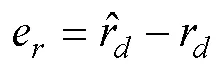
定義濾波誤差的導(dǎo)數(shù)為

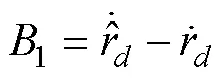
由式(31)可知, 偏航舵角等效控制律中包含艏搖角虛速度控制律的導(dǎo)數(shù)、執(zhí)行器幅值受限項和洋流擾動項。文中設(shè)計了干擾觀測器以降低洋流擾動對欠驅(qū)動AUV控制系統(tǒng)穩(wěn)定的影響, 采用濾波器降低了艏搖角虛速度直接求導(dǎo)計算的復(fù)雜度, 并且針對執(zhí)行器輸入受限設(shè)計了自適應(yīng)神經(jīng)網(wǎng)絡(luò)的滑模控制器。此外, 為降低滑模控制的抖振, 采用飽和函數(shù)代替符號函數(shù)sgn()。

選取Lyapunov函數(shù)

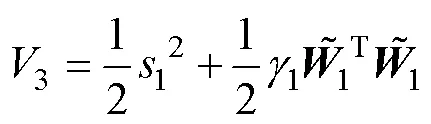
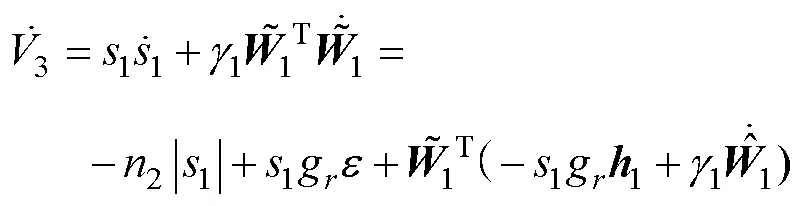
設(shè)計基于滑模面的自適應(yīng)律為

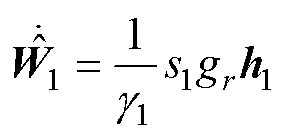
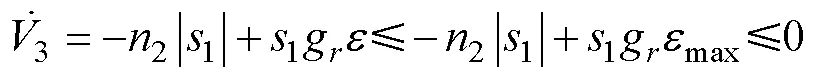
選取Lyapunov函數(shù)

根據(jù)Young’s不等式, 可得

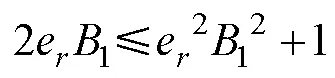
則有

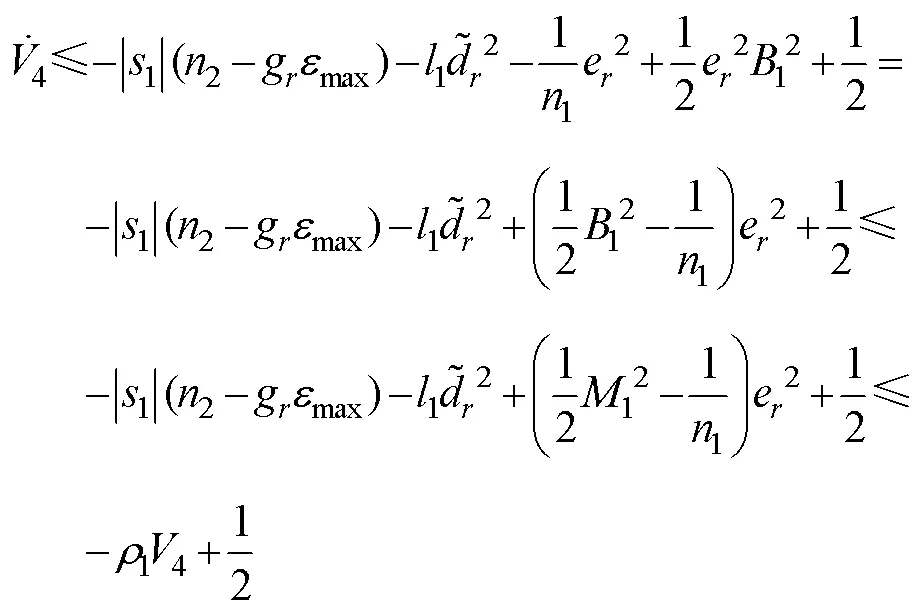
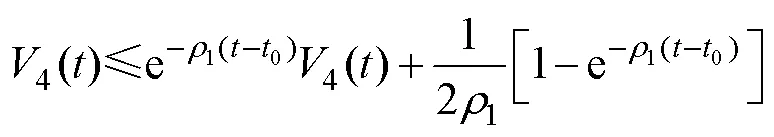
2) 浪涌速度跟蹤控制

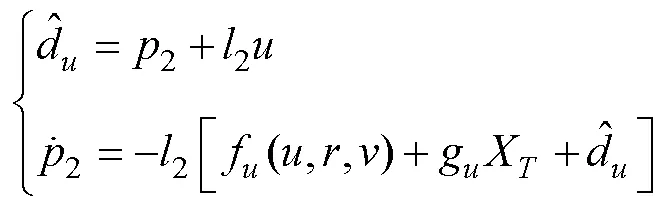
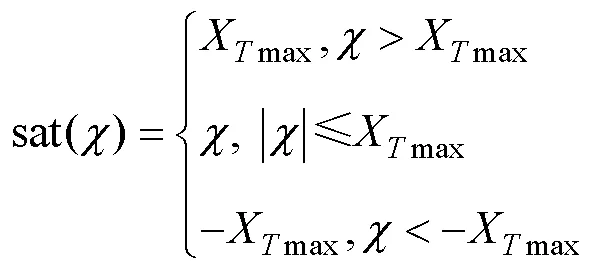
同樣, 通過神經(jīng)網(wǎng)絡(luò)RBF估計為

定義浪涌速度誤差為

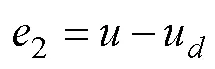
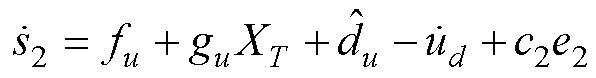
設(shè)計如下濾波器估計

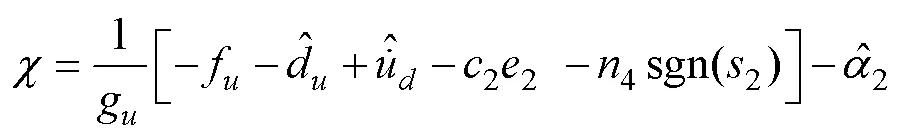
同樣設(shè)計神經(jīng)網(wǎng)絡(luò)權(quán)值自適應(yīng)律為

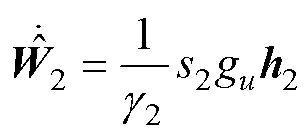
選取Lyapunov函數(shù)

根據(jù)Young’s不等式, 可得

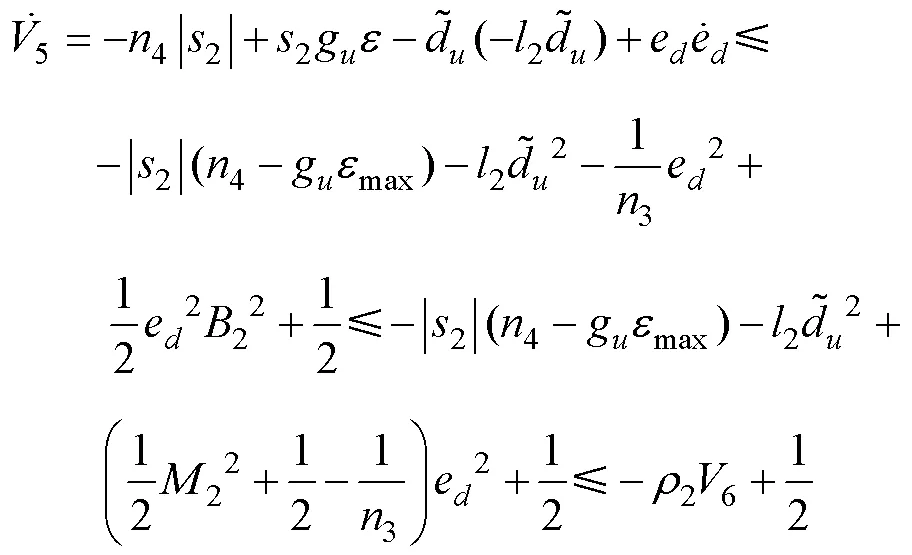
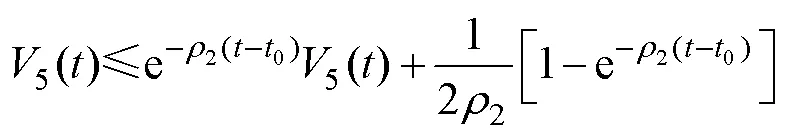
3 仿真驗證

為了更好地體現(xiàn)文中設(shè)計控制器的有效性, 采用仿真驗證所提軌跡跟蹤控制器的有效性和魯棒性。在著名的REMUS AUV上進行了數(shù)值仿真, AUV模型的參數(shù)如表1所示。

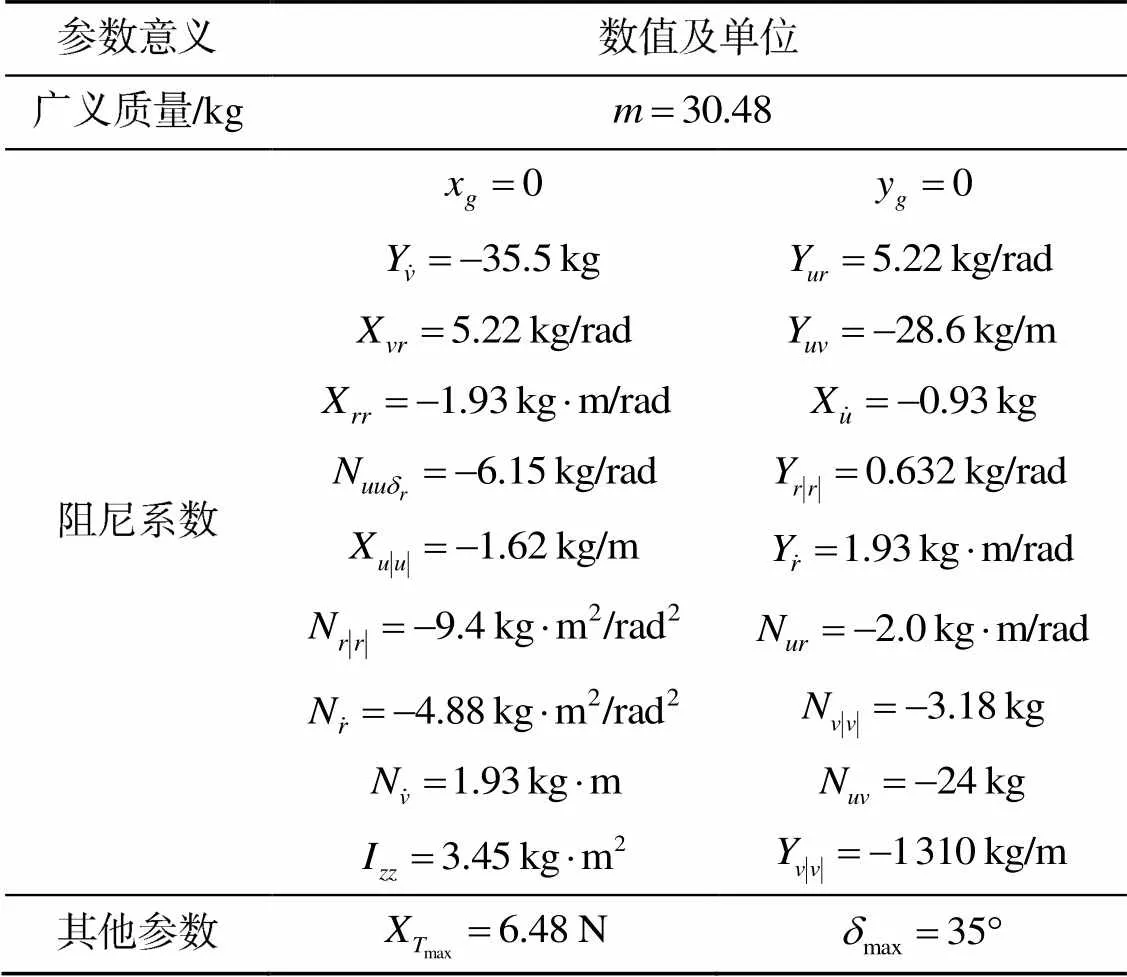
表1 AUV模型參數(shù)

在仿真驗證過程中, 選取了直線軌跡跟蹤和曲線軌跡跟蹤。

直線軌跡為

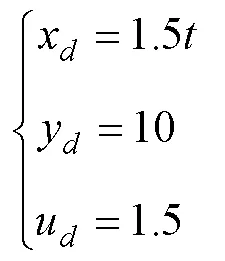
圖4 坐標(biāo)跟蹤曲線

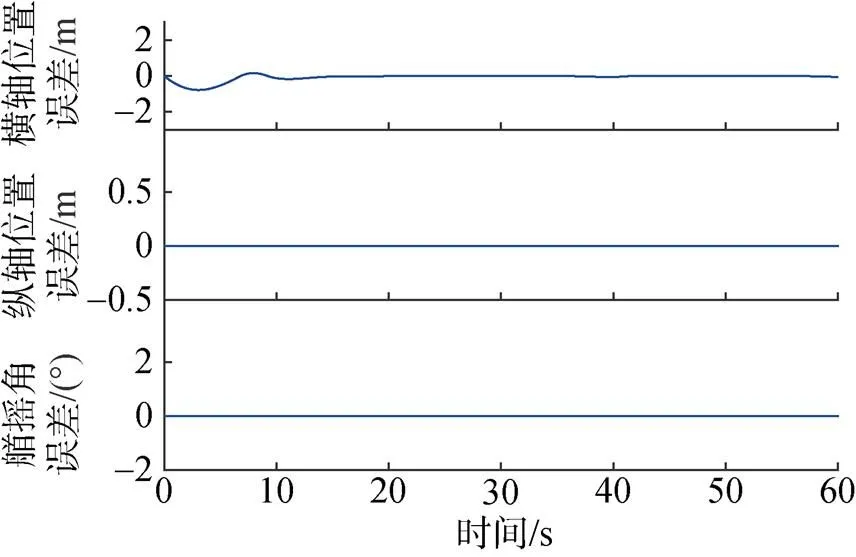
圖5 位置跟蹤誤差曲線

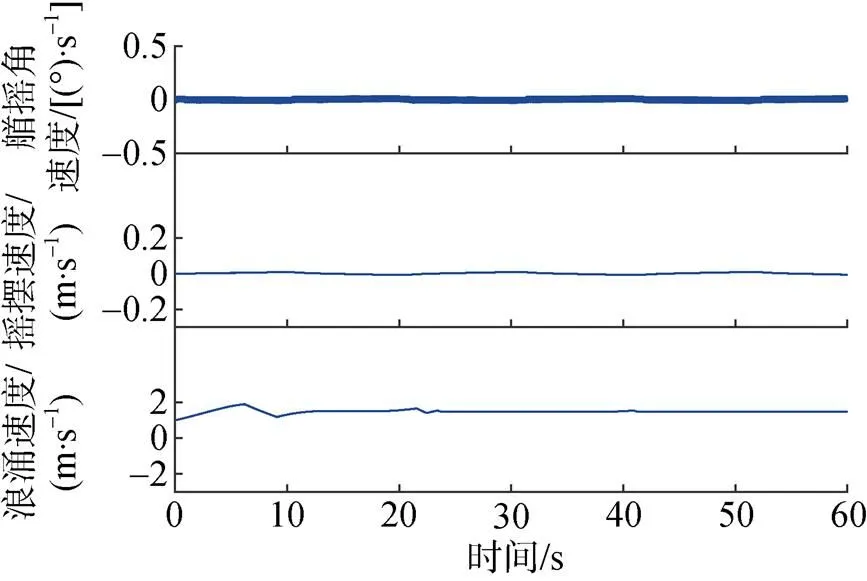
圖6 欠驅(qū)動AUV速度跟蹤曲線

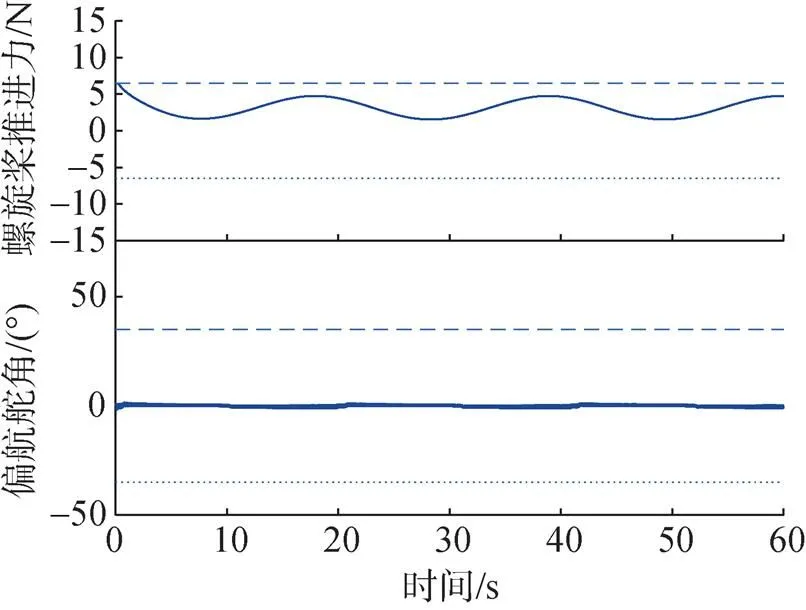
圖7 推進力和偏航舵角曲線

曲線跟蹤軌跡設(shè)定為

圖8和圖9分別為欠驅(qū)動AUV坐標(biāo)的跟蹤曲線和正弦軌跡跟蹤曲線, 由仿真結(jié)果可以明顯看出, 未考慮輸入受限的控制器和考慮輸入受限所設(shè)計的控制器都能完成實現(xiàn)欠驅(qū)動AUV正弦軌跡的跟蹤, 但是在曲率較大的地方, 未考慮輸入受限的控制器跟蹤誤差較大。

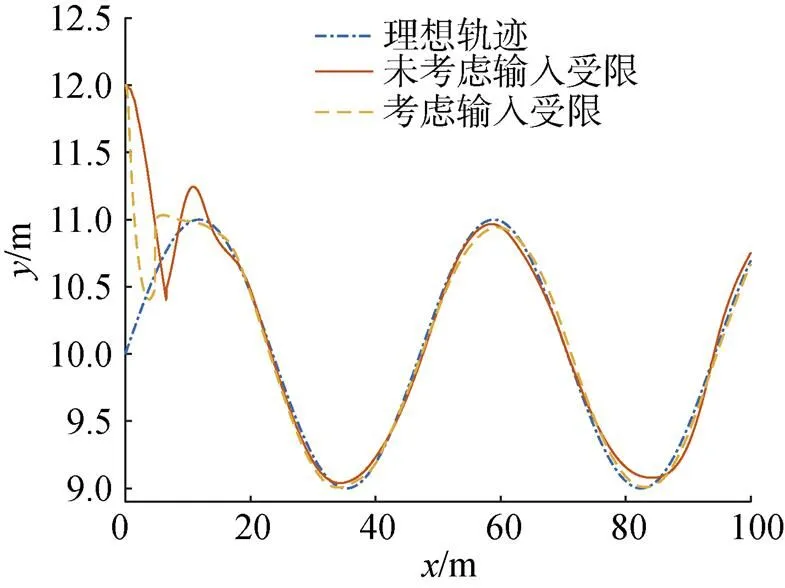
圖8 正弦軌跡跟蹤曲線

圖10中欠驅(qū)動AUV的位置和艏搖角跟蹤誤差能很快收斂到零點附近, 達到漸近穩(wěn)定, 但是由于擾動和輸入受限的影響, 文中設(shè)計的控制器收斂速度更快且位姿誤差更小。

圖11給出了欠驅(qū)動AUV速度誤差曲線。由仿真結(jié)果可以看出, 未考慮輸入受限的控制器和考慮輸入受限所設(shè)計的控制器都能收斂到理想速度, 但是文中設(shè)計的控制器的浪涌速度能更快收斂到理想速度且更為平緩, 艏搖角速度抖動幅度小且跟蹤精度高。

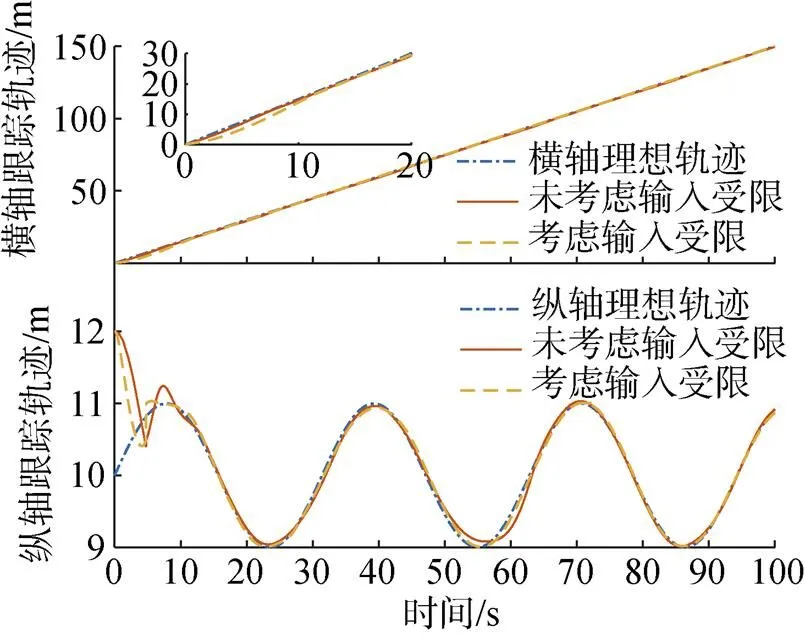
圖9 坐標(biāo)跟蹤曲線

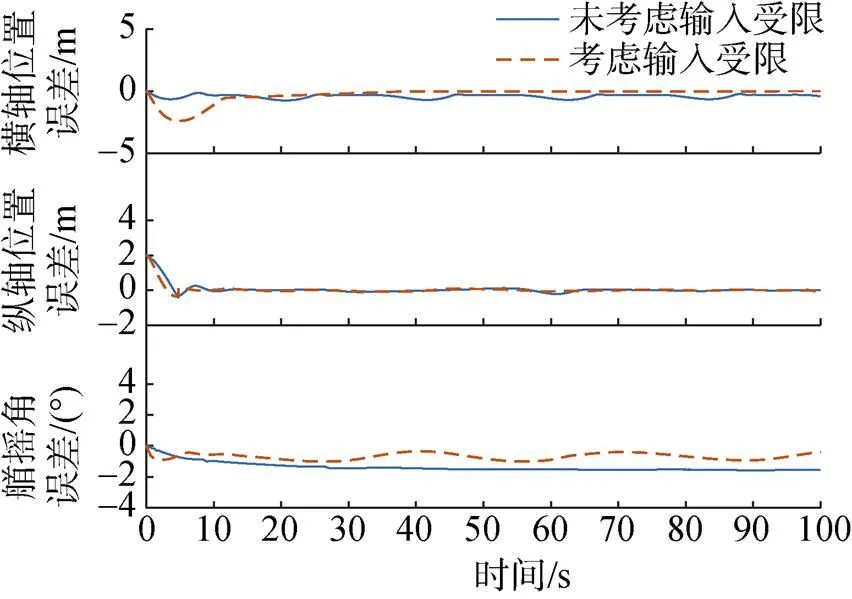
圖10 位置跟蹤誤差曲線

圖11 欠驅(qū)動AUV速度誤差跟蹤曲線

圖12和圖13為控制輸入的推進力、偏航舵角和神經(jīng)網(wǎng)絡(luò)補償?shù)那€以及局部放大圖。從圖12仿真結(jié)果可以看出, 考慮輸入受限下的推進力和偏航舵角能夠穩(wěn)定在預(yù)定范圍并且具有更平滑更快的響應(yīng)速度。從圖13的仿真的結(jié)果可以看出, 文中所設(shè)計的自適應(yīng)神經(jīng)網(wǎng)絡(luò)有較好的補償效果, 從而有效的解決了控制輸入受限的問題。

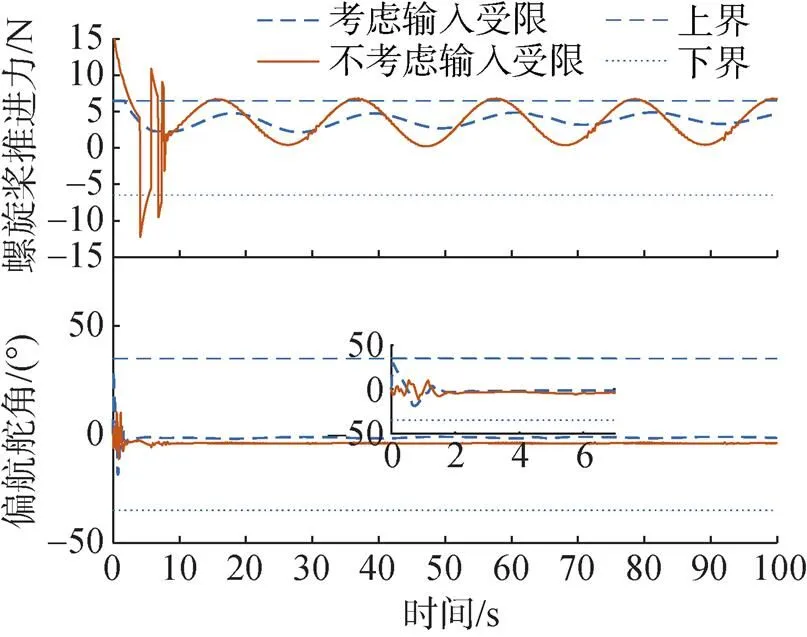
圖12 推進力和偏航舵角曲線

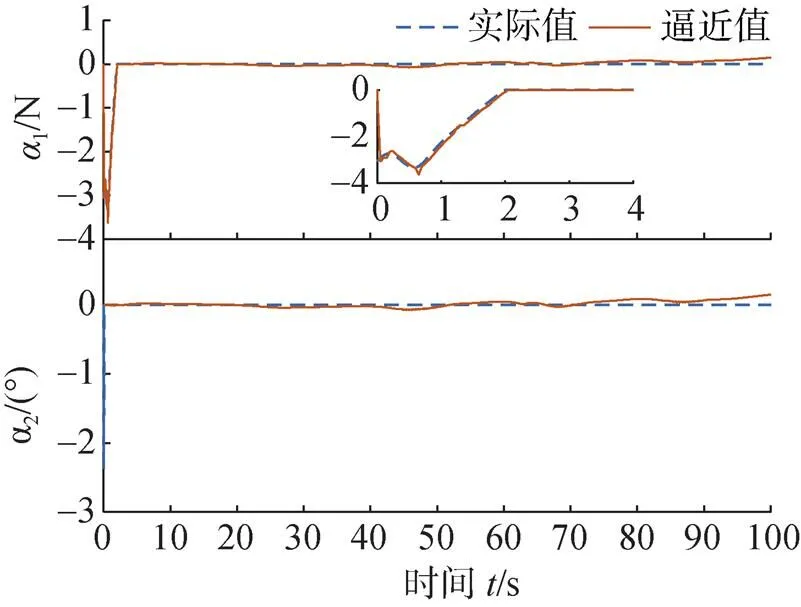
圖13 神經(jīng)網(wǎng)絡(luò)逼近曲線

4 結(jié)束語

針對AUV存在外界干擾和輸出受限影響下的控制問題, 提出了基于干擾觀測器和神經(jīng)網(wǎng)絡(luò)的滑模控制器。該控制器通過神經(jīng)網(wǎng)絡(luò)補償控制輸入受限, 使得AUV控制器的輸入保持在既定的邊界內(nèi), 提高了跟蹤精度, 得到了理想的跟蹤效果。仿真結(jié)果表明, 所設(shè)計的控制器能夠?qū)崿F(xiàn)AUV在水平面上的穩(wěn)定跟蹤控制。下一步的工作將針對欠驅(qū)動AUV在三維空間中的跟蹤控制, 并對所設(shè)計的控制器進行相應(yīng)的實驗驗證, 從而更好地說明所設(shè)計控制器的有效性和魯棒性。

[1] Johnsen G, Ludvigsen M, S?rensen A, et al.The Use of Underwater Hyperspectral Imaging Deployed on Remotely Operated Vehicles-methods and Applications[J].IFAC Papers Online, 2016, 49(23): 476-481.

[2] Li Z, Yang C, Ding N, et al.Robust Adaptive Motion Control for Underwater Remotely Operated Vehicles with Velocity Constraints[J].International Journal of Control Automation & Systems, 2012, 10(2): 421-429.

[3] Zhang G C, Huang H, Qing H D, et al.A Novel Adaptive Second Order Sliding Mode Path Following Control for a Portable AUV[J].Ocean Engineering, 2018, 151: 82-92.

[4] 熊華勝, 邊信黔, 施小成.積分變結(jié)構(gòu)控制原理在AUV航向控制中的應(yīng)用仿真[J].船舶工程, 2005(5): 30-33.

[5] Liang X, Qu X, Wang N, et al.Three-Dimensional Trajectory Tracking of an Underactuated AUV Based on Fuzzy Dynamic Surface Control[J].IET Intelligent Transport Systems, 2019, 14(5): 364-370.

[6] 鄧非, 尹洪東, 段夢蘭.基于AUV軌跡追蹤的優(yōu)化UKF算法[J].船舶工程, 2018, 40 (S1): 206-211, 229.

[7] Wang L L, Pan L X.Adaptive Variable Structure Control with Neuron for Path Tracking of Beaver AUV[J].IEEE Access, 2020, 8: 48566-48575.

[8] Che G, Zhen Yu.Neural-network Estimators Based Fault- tolerant Tracking Control for AUV via ADP with Rudders Faults and Ocean Current Disturbance[J].Neurocomputing, 2020, 411: 442-454.

[9] Cho G R, Park D G, Kang H, et al.Horizontal Trajectory Tracking of Underactuated AUV Using Backstepping Approach[J].IFAC-Papers Online, 2019, 52(16): 174-179.

[10] Xia Y, Xu K, Li Y, et al.Improved Line-of-sight Trajectory Tracking Control of Under-actuated AUV Subjects to Ocean Currents and Input Saturation[J].Ocean Engineering, 2019, 174(15): 14-30.

[11] Sarhadi P, Noei A R, Khosravi A.Adaptive Integral Feedback Controller for Pitch and Yaw Channels of an AUV with Actuator Saturations[J].Isa Transactions, 2016, 65: 284-295.

[12] Yu C, Xiang X, Zhang Q, et al.Adaptive Fuzzy Trajectory Tracking Control of an Under-Actuated Autonomous Underwater Vehicle Subject to Actuator Saturation[J].International Journal of Fuzzy Systems, 2018, 20(1): 269-279.

[13] 江夢潔, 李家旺, 呂艷芳, 等.飽和輸入限制下欠驅(qū)動自主水下航行器水平面軌跡跟蹤控制[J].兵工學(xué)報, 2017, 38(11): 2207-2213.

Jiang Meng-jie, Li Jia-wang, Lü Yan-fang, et al.Path Tracking Control of Underactuated Autonomous Underwater Vehicles on Horizontal Plane within Input Saturation Limit[J].Acta Armamentarii, 2017, 38(11): 2207- 2213.

[14] 楊立平, 張銘鈞, 褚振忠, 等.水下機器人抗積分飽和控制及主動容錯控制方法[J].哈爾濱工程大學(xué)學(xué)報, 2010, 31(6): 755-761.

Yang Li-ping, Zhang Ming-jun, Chu Zhen-zhong, et al.Anti-windup Control and Active Fault Tolerant Control Methods for Autonomous Underwater Vehicles[J].Journal of Harbin Engineering University, 2010, 31(6): 755-761.

[15] 王芳, 萬磊, 李曄, 等.欠驅(qū)動AUV的運動控制技術(shù)綜述[J].中國造船, 2010, 51(2): 227-241.

Wang Fang, Wan Lei, Li Ye, et al.A Survey on Development of Motion Control for Underactuated AUV[J].Shipbuilding of China, 2010, 51(2): 227-241.

[16] Sarhadi P, Noei A R, Khosravi A.Adaptive Integral Feedback Controller for Pitch and Yaw Channels of an AUV with Actuator Saturations[J].ISA Trans, 2016, 65: 284-295.

[17] Fossen T I.Guidance and Control of Ocean Vehicles[M].New York: John Wiley & Sons Inc, 1994.

Underactuated AUV Trajectory Tracking Sliding Mode Control with Input Limitation

LI Xin-bin, WANG Peng, LUO Xi, PANG Hong-tao

(Engineering Research Center of the Ministry of Education for Intelligent Control System and Intelligent Equipment, Yanshan University, Qinhuangdao 066004, China)

Aiming at the horizontal plane trajectory tracking problem of the underactuated autonomous undersea vehicle (AUV) under external interferences and limited inputs, a sliding mode controller based on a nonlinear disturbance observer and radial basis function(RBF) neural network was proposed in this study.Firstly, the underactuated AUV kinematics model was transformed into an error kinematics model to stabilize the position error through a coordinate transformation.Secondly, the backward step method was used to design the bow-rocking angle virtual velocity control law to stabilize the attitude error.Subsequently, a nonlinear disturbance observer was used to estimate the disturbance of a time-varying ocean current, and the derivative of the virtual control law was estimated through a filter to avoid the “differential explosion” caused by the derivative of the virtual control law.Finally, an adaptive RBF neural network was designed to compensate the actual input of the underactuated AUV, and the Lyapunov stability proved that the signal used for the closed-loop tracking error was uniformly bounded.The simulation verified the effectiveness of the designed controller.

underactuated autonomous undersea vehicle; input limitation; trajectory tracking; sliding mode

李鑫濱, 王鵬, 駱曦, 等.輸入受限下欠驅(qū)動AUV軌跡跟蹤滑模控制[J].水下無人系統(tǒng)學(xué)報, 2022, 30(1): 44-53.

TJ630.1; TB71.2

A

2096-3920(2022)01-0044-10

10.11993/j.issn.2096-3920.2022.01.006

2021-03-29;

2021-06-04.

國家自然科學(xué)基金項目資助(61873224); 河北省省級科技計劃項目資助(F2020203037).

李鑫濱(1969-), 男, 博士, 教授, 主要研究方向為水下機器人智能控制.

(責(zé)任編輯: 許 妍)